Ecuaciones con dos incógnitas
Ecuaciones con dos incógnitas
Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.
Énfasis: formular un sistema de ecuaciones lineales 2×2 que permita resolver una situación de diferentes maneras.
¿Qué vamos a aprender?
Partirás de conocimientos que adquiriste en primer grado de secundaria, sobre las ecuaciones lineales o también llamadas ecuaciones de primer grado y sus componentes. Estos conocimientos te serán de utilidad en la resolución de otro tipo de ecuaciones.
En esta sesión, conocerás cómo plantear y resolver sistemas de dos ecuaciones lineales con dos incógnitas; utilizando distintos métodos como el gráfico, el de igualación, el de sustitución, y el método de suma y resta. También identificarás que al resolver algunos sistemas de ecuaciones lineales con dos incógnitas puede suceder que:
- Algunos tienen solución única,
- Otros tienen un número infinito de soluciones y
- Algunos más no tienen solución.
Al estudiar distintos métodos algebraicos para formular y solucionar sistemas de dos ecuaciones lineales con dos incógnitas, observarás que todo método implica un orden. Pero esto no significa que tengas que memorizar cada paso o método, sino que comprendas en qué consiste cada uno de estos métodos y utilizarlos en la resolución de problemas algebraicos.
¿Qué hacemos?
Antes de profundizar en el tema, lee un extracto de la obra “El modelo matemático náhuatl, la danza y los juegos tradicionales: prácticas sociales matemáticas”, capítulo primero “Fundamento matemático de la cuenta de la simplicidad de la armonía”, del autor Everardo Lara González.
Fundamento matemático de la cuenta de la simplicidad de la armonía
Trascedente en la evolución de la humanidad ha sido descubrir el conocimiento de las matemáticas, en las que, jerárquicamente, se encuentra el valor del supremo ordenador, que describe con sabiduría las cualidades divinas de la simplicidad de la armonía.
La ciencia demuestra que hay leyes matemáticas que revelan una armonía superior de la razón a pesar de la complejidad del mundo: las ideas y formas matemáticas son el modelo de la perfección del todo; concepción que se ilustra claramente en las formas geométricas.
En el transcurso de la historia varios pueblos se preocuparon por el estudio de las matemáticas, creando y desarrollando diferentes símbolos que detentaron las ideas y formas descritas. Así surge la escritura y, por ende, los numerales, que representan ideas, formas, mensajes o a veces sólo cifras. De ese modo los seres humanos aprendieron a registrar el comportamiento ordenado que habían descubierto en el cielo y en la naturaleza, lo que les ha permitido, a través de la historia, predecir eventos que benefician o afectan nuestra supervivencia en equilibrio con el todo.
El modelo matemático náhuatl, la danza y los juegos tradicionales: prácticas sociales matemáticas
Everardo Lara González
El extracto que leíste lleva a un viaje por la Historia, mostrando cómo necesidades, y exigencias, el medio que le presentaba al ser humano, le brindaba la oportunidad de experimentar, conocer y comprobar nuevas cosas.
En esta experiencia, el ser humano, construía conocimientos matemáticos que le permitían predecir eventos favorecedores y también algunos no tan favorecedores a su medio. El conocimiento matemático impulsa el razonamiento, la reflexión y la lógica.
A continuación, presta mucha atención en el siguiente caso:
Al revisar su libro de texto, Joshua leyó lo siguiente:
Dada la siguiente ecuación, plantea un problema que se pueda resolver con ella:
x + 2x = 24
¿Qué problema o situación plantearías?
Analiza cómo Joshua, realizó la propuesta en su libro de texto de matemáticas de segundo de secundaria.
Joshua tiene dos amigos que son hermanos. Así que pensó en relacionar la edad de Ana y de su hermano David, con la ecuación. Y la escribió de la siguiente manera:
“Ana tiene el doble de la edad de su hermano David y la suma de sus edades es igual a 24”.
¿Cómo se puede conocer qué edad tienen Ana y su hermano David?
¿Consideras que es posible determinar la edad de Ana y la edad de David?
¿Cómo lo harías?
Para resolver el problema, primero se representa de manera algebraica la situación que modeló Joshua.
Con la literal x se representa a la incógnita, que en este caso corresponde a la edad de David, ésta también será útil para calcular la edad de Ana, pues en el planteamiento se da una condición: la edad de Ana es el doble de la edad de David.
Por lo tanto, en la siguiente tabla puedes observar cómo se pasa del lenguaje común al lenguaje algebraico para representar la situación:
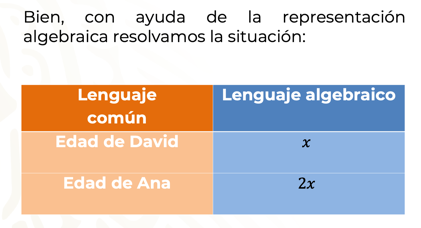
Entonces, al relacionar las condiciones de la situación, se verifica que se cumple con la ecuación lineal o de primer grado:
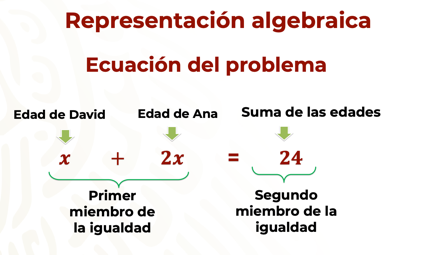
x que representa la edad de David, más 2x que representa la edad de Ana, es igual a 24, que es la suma de las edades.
Para resolver la ecuación, es decir, para calcular el valor de “x”, primero se reducen términos semejantes en el primer miembro de la ecuación, de este modo tenemos como resultado: 3x = 24.
Para calcular el valor de “x”, se puede interpretar esta ecuación de dos formas:
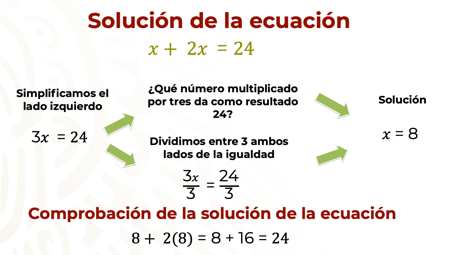
Para comprobar la solución de la ecuación y verificar que las edades de David y Ana son 8 y 16 respectivamente, se sustituye x por su valor numérico, y se resuelven las operaciones.
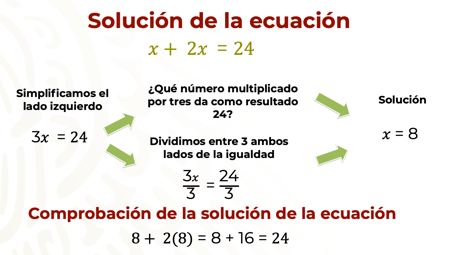
Entonces, ya sabes que David tiene 8 años y que Ana tiene 16 años. Has resuelto el planteamiento diseñado por Joshua.
Antes de continuar, recuerda a detalle algunos elementos que son necesarios para representar y resolver ecuaciones. Para ello, responderás qué es un coeficiente y repasarás los elementos de una ecuación de primer grado.
¿Qué es un coeficiente?
Un factor multiplicativo, es un número o constante que se encuentra generalmente a la izquierda de la literal, en este caso la incógnita, y que representa una multiplicación.
Por ejemplo:
- 5 veces la edad de una persona: 5x
El coeficiente de x es 5. - 3 veces el precio de un chocolate: 3y
El coeficiente de y es 3. - El área de un rectángulo de base 3x y de altura z: A = 3xz
El coeficiente de x es 3 y el de z es 1
Elementos de una ecuación de primer grado
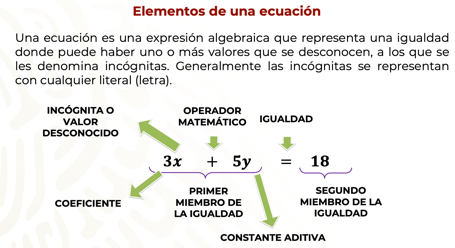
Una ecuación es una expresión algebraica que representa una igualdad donde puede haber uno o más valores que se desconocen, a los que se les denomina incógnitas. Generalmente las incógnitas se representan con cualquier literal (letra).
En una ecuación, a la expresión que se encuentra a la izquierda de la igualdad se le llama primer miembro y a la que está a la derecha, segundo miembro.
En la ecuación 3x + 5 = 18, el primer miembro es 3x + 5 y el segundo miembro es 18.
La incógnita o valor desconocido es x, el coeficiente es 3, y la constante aditiva es 5.
Elementos de una ecuación de primer grado
Una ecuación es una expresión algebraica que representa una igualdad donde puede haber uno o más valores que se desconocen, a los que se les denomina incógnitas. Generalmente las incógnitas se representan con cualquier literal (letra).
En una ecuación, a la expresión que se encuentra a la izquierda de la igualdad se le llama primer miembro y a la que está a la derecha, segundo miembro.
En la ecuación 3x + 5 = 18, el primer miembro es 3x + 5 y el segundo miembro es 18.
La incógnita o valor desconocido es x, el coeficiente es 3, y la constante aditiva es 5.
Ahora, observa y analiza el siguiente ejercicio:
Encuentra dos números cuya suma sea 37 y su diferencia sea 9.
Primero, analiza los elementos:
- Tienes dos valores por encontrar, es decir, los dos números que desconoces.
- Tienes dos igualdades, una que representa una suma, y otra que representa una resta.
- Por lo tanto, al tener dos igualdades tienes: dos ecuaciones, es decir, dos ecuaciones con dos incógnitas en cada ecuación.
- Al primer sumando se le restará el segundo.
Al representar algebraicamente la situación anterior, obtienes las siguientes ecuaciones:
Se usarán las literales “x” y “y” para representar a las incógnitas.
Primera y segunda condición:

Al par de ecuaciones que representan la situación se les conoce como sistema de ecuaciones lineales 2 x 2.
Realiza algunos intentos:
Busca números que cumplan con las condiciones dadas en el problema.
Por ejemplo:
Primer intento.

20 y 17, la suma de estos números es igual a 37
¿Pueden ser 20 y 17 soluciones del sistema de ecuaciones?
No, porque, aunque la suma de 20 + 17 es igual a 37, no cumplen la segunda condición, es decir, la diferencia de estos números no es 9. Porque 20 – 17 = 3.
Segundo intento.

21 y 12. Con estos números se cumple con la segunda condición, pero no pueden ser solución del sistema de ecuaciones porque la suma es igual a 33.
Estás dos parejas de números tampoco cumplen con las dos condiciones del problema.
Tercer intento.
Ahora prueba con los siguientes números: 23 y 14.

Observamos que, la suma de ellos es: 23 + 14 = 37 y su diferencia es 23 – 14 = 9
Has llegado a la solución. Los números que cumplen con las dos condiciones del problema son 23 y 14.
El procedimiento que se utilizó para encontrar los números que dan solución al problema propuesto es conocido como ensayo y refinamiento, al ir probando distintas parejas de números, hasta encontrar los valores numéricos de las incógnitas que cumplen con las condiciones del problema y con ello llegar a la solución.
Sin embargo:
¿Piensas que haya otra forma de resolver problemas que impliquen dos ecuaciones con dos incógnitas en cada ecuación?
En matemáticas hay diferentes maneras de resolver los planteamientos, y en este caso, otra manera es utilizar un registro tabular o tabla de datos.
La representación de datos en una tabla es útil para organizarlos y sistematizarlos, como se muestra.
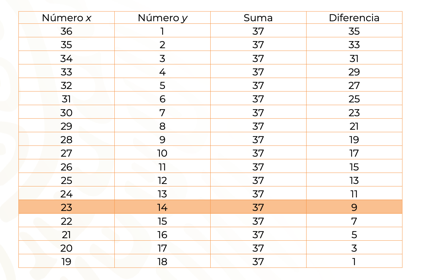
Se colocan los posibles valores del número “x”, así como los posibles valores del número “y”, mismos que su suma sea 37, y su diferencia sea 9.
La primera pareja de números es 36 y 1, suman 37, pero la diferencia no cumple con la condición dada.
La segunda pareja de números, 35 y 2, suman 37, pero la diferencia no cumple con la condición dada, y así sucesivamente hasta que se identifica la pareja de números que cumple con las dos condiciones del problema, que son 23 y 14.
A continuación, analiza otro problema e intenta resolver la siguiente situación. Después, valídala.
Las compras en el mercado
La señora Angélica fue al mercado y compró 2 kilogramos de tomate y 1 kilogramo de cebolla, y pagó $55.00, en total.
En el mismo puesto, la señora Silvia compró 1 kilogramo de tomate y 2 kilogramos de cebolla, y pagó $50.00.
¿Cuál es el precio de un kilogramo de tomate?
¿Cuál es el precio de un kilogramo de cebolla?
Para resolver este tipo de problemas, es necesario conocer otro método, el cual profundizarás durante las siguientes sesiones y se le llama sistema de ecuaciones simultáneas de 2 x 2, es decir, son dos ecuaciones y dos incógnitas.
Presta mucha atención al planteamiento de un sistema de ecuaciones 2×2 que representa el problema propuesto, para saber cuánto cuesta un kilogramo de tomate y un kilogramo de cebolla.
Primero se establece el sistema de ecuaciones lineales que represente el problema, para validar su postura. Para ello, “x” será la cantidad de jitomate en kilogramos y “y” la cantidad de cebolla.

El costo de los dos kilogramos de tomate, que es dos “x”, más el costo del kilogramo de cebolla, que es “y”, es igual a 55, que es lo que la señora Angélica pagó.
El costo del kilogramo de tomate que es “x”, más el costo de los dos kilogramos de cebolla que es dos “y”, es igual a 50, que es lo que la señora Silvia pagó.
Y es así como se determinan las dos ecuaciones que forman el sistema de ecuaciones lineales 2 x 2.
2x + y = 55
x + 2y = 50
Una vez determinado el sistema de ecuaciones lineales 2 x 2, se debe encontrar el valor de “x” y de “y”, que satisfagan ambas igualdades en las ecuaciones.
Es así como se representa algebraicamente la situación.

Ahora, usa una de las técnicas que hay para determinar los valores de las incógnitas en un sistema de ecuaciones 2 x 2, esta técnica es conocida como ensayo y refinamiento. Mediante la estimación numérica asigna números hasta que se encuentra la respuesta correcta.
En búsqueda de las soluciones del sistema de ecuaciones:
“x”, representa el costo del kilogramo de tomate.
“y” representa el costo del kilogramo de cebolla.
Intenta resolver las ecuaciones con:
x = 15
y = 25.

Analiza las ecuaciones y trata de aproximarte, para ello, asigna diferentes valores a “x” y a “y”, sustituye las incógnitas por los valores asignados y comprueba si se cumple la igualdad en ambas ecuaciones.
Inténtalo ahora con otros valores para “x” y “y”.
¿Qué valores encontraron para “x” y “y”?
¿Cuánto cuesta un kilogramo de cebolla y cuánto un kilogramo de tomate?
Una vez que hayas encontrado la solución, compruébala.
Es importante realizar la comprobación de los valores de las incógnitas en un sistema de ecuaciones lineales.
- Comprobar las soluciones en un sistema de ecuaciones 2 × 2, es verificar que los valores encontrados para las incógnitas hacen que se cumpla la igualdad en ambas ecuaciones.
- Para ello, se reemplazan las incógnitas por sus valores numéricos en ambas ecuaciones y verificamos que se cumpla la igualdad.

Ahora puedes responder las preguntas:
¿Cuánto cuesta un kilogramo de cebolla y cuánto un kilogramo de tomate?
Un kilogramo de tomate cuesta 20 pesos y un kilogramo de cebolla cuesta 15 pesos.
Resuelve un último problema.
Una maestra les propuso a las y los estudiantes que plantearan un problema que se pudiera representar y resolver con el siguiente sistema de ecuaciones lineales 2 x 2:
Ecuación 1x + y = 47
Ecuación 2x – y = 3
¿Qué contexto podrías utilizar para representar el sistema de ecuaciones?
Escribe en tu cuaderno un problema que se resuelva con el sistema de ecuaciones expuesto.
¿Cuáles son las soluciones del sistema de ecuaciones?
Observa las propuestas que hicieron dos alumnos y cómo resolvieron el sistema de ecuaciones. En este caso, se cambiará del lenguaje algebraico al lenguaje común.
Diana:
En una tienda tienen perfumes de dama y de caballero almacenados en una caja. En total tienen 47 perfumes, el número de perfumes para dama rebasa al número de perfumes para caballero en tres piezas. ¿Cuántos perfumes hay de cada tipo?
Si los perfumes de dama se representan con la literal “x”, y los de caballero, con “y”, se tiene que:

Efraín:
Entre Isaac y Gabriel tienen 47 carros de juguete, de colección. Si Isaac tiene 3 carros más que Gabriel, ¿cuántos carros tiene cada uno?
Se representa con “x” a los carros de Isaac y con y” a los carros de Gabriel, se tiene que:

Ahora, observa cómo resolvió el sistema de ecuaciones Diana:

Diana después de dos pruebas, encontró una solución en su tercera opción.
Ahora, observa cómo lo resolvió Efraín.

Se utilizaron diferentes contextos y se obtuvieron las mismas soluciones del sistema de ecuaciones:
x = 25
y = 22
Además, con el procedimiento de Efraín, aprendiste otra manera de resolver un sistema de ecuaciones lineales 2 x 2, con el apoyo de un registro tabular.
También conociste cómo usar la técnica del ensayo y refinamiento, pero imagina que tienes que encontrar la suma de dos números que den 36 254 y la diferencia sea 29 256.
¿Cómo se resolvería?
Observa el siguiente ejemplo sobre cómo solucionar este tipo de problemas:

Al representar algebraicamente la situación, se establecen dos ecuaciones, con dos incógnitas en cada una. Como se mencionó antes, a este tipo de ecuaciones se les conoce como sistema de ecuaciones simultáneas de 2 x 2, es decir son dos ecuaciones y dos incógnitas.

Donde “x” y “y” representan las incógnitas y a, b, d, y e, representan sus coeficientes, los cuales deben ser los valores que satisfacen ambas igualdades.
Se usa una llave para identificar que ambas ecuaciones corresponden a un sistema 2 x 2.
Ahora que ya sabemos qué es un sistema de ecuaciones lineales 2 x 2
¿Cómo se pueden determinar los valores de “x” y de “y” para que se cumplan ambas igualdades?
Para ello debes tener muy claro que: resolver un sistema de ecuaciones lineales con dos incógnitas, significa encontrar los valores de las incógnitas que permiten que se cumpla la igualdad de cada ecuación del sistema.
Al resolver el sistema de ecuaciones lineales 2 x 2 anterior, las soluciones son:

“x” = 32 755 y “y” = 3 499, porque la suma de 32 755 y 3 499 es 36 254, y su diferencia es 29 256, como puedes ver en la imagen anterior al comprobar las soluciones del sistema.
Poniendo en juego el cálculo mental y escrito, se desarrollan habilidades. Así como en el pasado los seres humanos lo hacían y como leíste en el extracto del autor Everardo Lara González, en la lectura que realizaste al inicio.
El reto de hoy:
Consulta tu libro de texto de Matemáticas, segundo grado, para repasar lo referente a los sistemas de ecuaciones lineales 2 x 2.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/