Desarrollo del binomio al cuadrado II
Desarrollo del binomio al cuadrado II
Aprendizaje esperado: resuelve problemas que implican el uso de ecuaciones de segundo grado.
Énfasis: resolver problemas cuadráticos usando factorización.
¿Qué vamos a aprender?
En sesiones anteriores has realizado factorizaciones utilizando técnicas como binomios conjugados, binomios con factor común, diferencia de cuadrados.
Resolverás problemas cuadráticos utilizando la técnica del desarrollo del binomio al cuadrado.
En caso de que no cuentes con el libro de texto, tienes la opción de consultarlo a través de la página de la Comisión Nacional de Libros de Texto Gratuitos.
Procura recrear en tu cuaderno las figuras y las soluciones que se presentarán.
No olvides registrar tus dudas, inquietudes y anotaciones respecto a esta lección. Podrás apoyarte en tu libro de texto para consolidar los aprendizajes.
¿Qué hacemos?
Conocerás a un personaje que dejó huella en la historia de las matemáticas, cuando escuches su nombre te darás una idea de donde proviene, él vivió en el año 720 de nuestra era, hace unos 1280 años y fue astrónomo, geógrafo y por supuesto un gran matemático: Al-Khwarizmi, como su nombre es tan distintivo pueden suponer su procedencia.
Su origen es árabe, él escribió un libro de álgebra en el cual resolvía seis tipos de ecuaciones, dichas ecuaciones se construyen con tres tipos de cantidades raíces, cuadrados de raíces y números; esto es, x, x^2 y números.
Al analizar parece ser lo que conoces como lenguaje común, observa la siguiente tabla donde se representan las ecuaciones en comparación con las expresiones actuales.
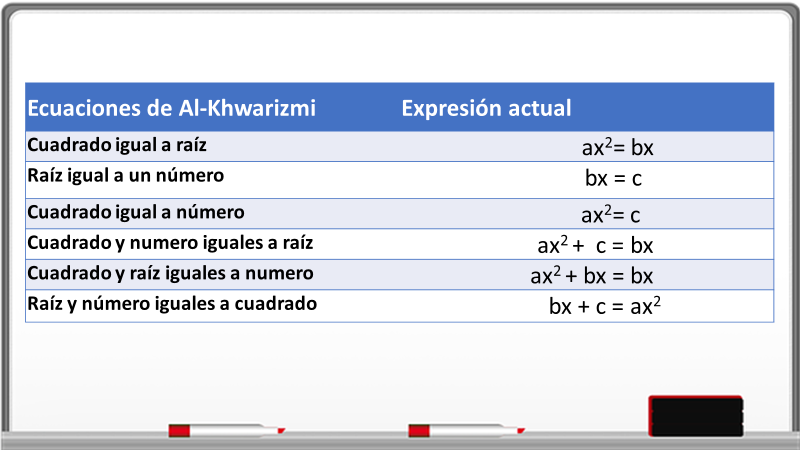
¿Reconoces alguna de las expresiones actuales, es decir las de la columna derecha?
Existen ecuaciones de segundo grado o también llamadas cuadráticas. Esto indica que desde hace tiempo se han utilizado las ecuaciones cuadráticas para resolver situaciones o problemas donde la aritmética tiene poco alcance o definitivamente no tiene forma de resolverlas.
Remóntate a 2000 años antes de nuestra era, a la cultura babilónica. Entre los vestigios de esta cultura se encontró una tablilla cuneiforme en donde, hay evidencia de la solución de un problema con ecuaciones de segundo grado y ésta es:

Como puedes darte cuenta, al analizar el problema escrito en la tablilla, es fácil de interpretar lo que se quiere calcular —además de involucrar a un polígono—, el cuadrado ¿Será mera coincidencia o desde hace mucho tiempo los problemas son iguales o parecidos a los que se tienen en la actualidad?
Aprenderás a utilizar una técnica para resolver este tipo de problemas que te permiten calcular las raíces de la ecuación. ¿Cómo lo resolvían los babilonios? No se tiene respuesta a esa pregunta, pero conocerás una técnica para resolver problemas de esa índole.
En fin, sean iguales o parecidos los problemas que se planteaban hace tiempo, es precisamente lo que aprenderás, el cómo resolverlos. Utilizarás la técnica de factorización a partir del desarrollo de binomio al cuadrado.
Anteriormente, has utilizado diferentes técnicas y has representado geométricamente, mediante un rectángulo, la factorización de expresiones algebraicas.
Ahora utilizarás el cuadrado como la figura para representar el binomio al cuadrado.
En años anteriores aprendiste los productos notables, en esta sesión ocuparás los conocimientos que tengas, para esto analiza el siguiente video del minuto 4:40 a 9:17.
- Binomios al cuadrado
Con la información del video puedes enunciar que:

A esta expresión algebraica se le llama Trinomio cuadrado perfecto. Recuerda esta regla ya que será de gran utilidad para esta sesión.
Realiza la primera actividad.

Como puedes darte cuenta, todo lo que has aprendido en años anteriores se va ocupando para obtener otro conocimiento que te permitirá resolver problemas más complejos.
Hasta aquí has realizado un repaso de algunos contenidos específicos que te ayudarán en tu aprendizaje. Es momento de resolver ejercicios de factorización utilizando la técnica del binomio al cuadrado.
Resuelve la siguiente ecuación por factorización. Pero antes de resolverla debes de saber si la expresión algebraica es un trinomio cuadrado perfecto ¿Cómo lo puedes saber?

Una vez que compruebas que es un trinomio cuadrado perfecto, procede a factorizarlo; es decir, lo escribes como el producto de dos factores y en este caso los factores son binomios.
Continúa resolviendo la ecuación cuadrática.
Una forma para resolver la ecuación es a partir del valor absoluto del término independiente que es 16; es decir, no tomas en cuenta su signo ¿Cuáles serían sus divisores?
Por supuesto son: 1, 2, 4, 8, 16.
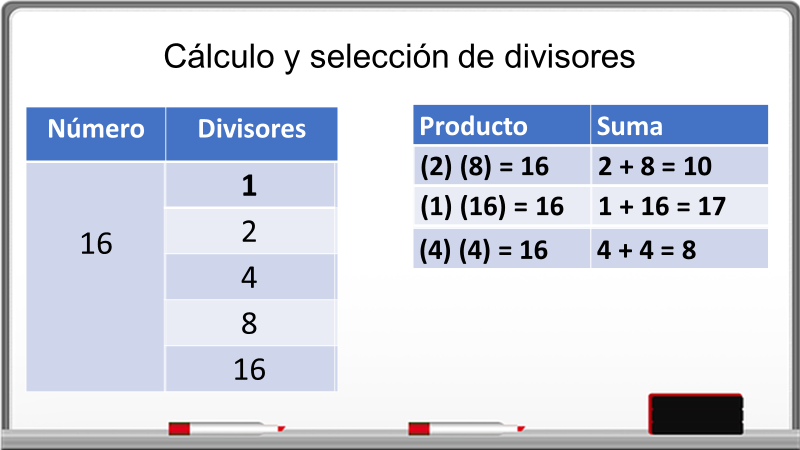
Ahora selecciona aquellos valores cuyo producto sea 16 que es el término independiente y, que al mismo tiempo estos dos valores sumados den como resultado 8 que es el coeficiente del término lineal.
Si ocupas los números 2 y 8, al multiplicarlos si obtienes 16, pero si lo sumas el resultado es 10 y requieres que sea 8, por lo que no son los valores que cumplan las condiciones.
Ahora considera 1 y 16, su producto es 16, pero sumados dan 17, tampoco cumplen con la segunda condición.
Tomas los números 4 y 4, al calcular su producto es 16 y sumados dan 8, ¿por qué será?
Recuerda lo que observaste en el video anterior. Estás utilizando la técnica de binomio al cuadrado, por lo que gráficamente la ecuación representa un cuadrado y esto indica que debes utilizar los mismos valores, esta información será útil para los próximos ejercicios y problemas.

Ya se encontró una expresión equivalente a la ecuación. Ahora sigue buscando la solución a la misma. El siguiente paso es igualar el producto de los binomios a 0, tal como estaba la ecuación.
Para que la ecuación sea igual a cero, implica que (x+4) ^2 es igual a cero; es decir, (x+4) = 0, quita los paréntesis.
Para despejar a x sumarás el inverso aditivo de 4 de cada uno de los miembros de la ecuación, quedando al final x = -4.

El resultado es 4 negativo. El 4 negativo que se obtuvo, representa el valor de la solución o raíz de la ecuación, en otras palabras, has resuelto la ecuación, pero ¿cómo saber si el resultado es correcto?
Para saber si el valor calculado de x es correcto, es necesario que realices la comprobación; es decir, sustituyes el valor de la incógnita en la ecuación y se realizan operaciones para determinar si se conserva la igualdad.
Realiza la comprobación. En la comprobación, sustituyes el valor de la incógnita que es x = -4 en la ecuación, realiza operaciones y observa si se conserva la igualdad.

Como puedes ver, se conserva la igualdad, por lo que la solución de la ecuación es correcta.
Ahora resuelve una ecuación en la que su término lineal (el que tiene la incógnita con exponente 1) es negativo.

En esta ocasión debes de calcular divisores positivos y negativos. Te preguntarás el porqué de los signos, si observaste la ecuación a resolver, el término lineal tiene signo negativo, ese es el motivo por el que estás considerando valores negativos. Recuerda, sólo utilizarás divisores cuya suma tenga como resultado 12 negativo y que su producto sea igual a 36.

De la tabla de divisores que se muestra, ¿cuáles cumplen con las condiciones mencionadas? Son 6 y 6 negativo, intenta con estos valores negativos y positivos.
Al multiplicar seis por seis, sean positivos o negativos, el resultado es 36, pero también necesitas que sumados sean igual a 12 negativo, por lo que 6 negativo es el valor que necesitas.
Al realizar la operación, 6 negativo y 6 negativo son los valores cuyo producto es igual a 36, y su suma es igual a 12 negativo, por lo que la factorización queda:

Como pudiste darte cuenta, en esta ecuación se calcularon divisores positivos y negativos para poder factorizar, en comparación con la ecuación anterior donde todos sus signos eran positivos.
El producto de los binomios obtenidos se iguala a 0, tal como la ecuación original. Al multiplicarse, queda un binomio al cuadrado. Para que el binomio al cuadrado sea 0, esto implica que x-6 = 0.

Despejando a “x”, obtienes su valor.
El resultado es 6, ahora falta saber si satisface a la ecuación, para ello realiza la comprobación
En la comprobación sustituyes el valor de la incógnita que es x=6 en la ecuación, realiza operaciones y observa si se conserva la igualdad.

Como puedes observar, se conserva la igualdad, por lo que la solución que calculas de la ecuación es correcta. Con esto terminas los ejercicios, ahora resuelve los problemas utilizando este método de factorización.
Resuelve el siguiente problema, donde se requiere no sólo de factorizar.
Una arquitecta que busca siempre la armonía entre la naturaleza y los espacios construidos elaboró un boceto para un proyecto de condominios horizontales en un terreno cuadrado como el que se muestra en la figura.
A fin de determinar la medida ideal del espacio que ocuparán los condominios, plantea el modelo matemático x^2 – 100x + 2500=1225 que representa el área total del terreno a partir del boceto que hizo.
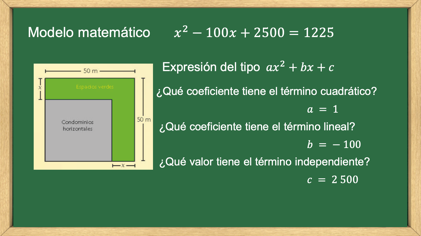
La expresión del modelo matemático es del tipo ax^2 + bx+ c. Las letras a, b y c representan números reales, positivos o negativos, x representa la incógnita, es decir el valor a calcular cuando se resuelva la ecuación.
¿Qué número representa a la letra a?
Efectivamente a = 1
¿Qué número representa b?
Para b = – 100
¿Qué número representa c?
Para c = 2500
Sabes que se trata de una ecuación cuadrática completa ya que tiene los tres términos, cuadrático, lineal, e independiente.
Una vez que tienes el trinomio cuadrado perfecto podrás factorizar y calcular el valor de la incógnita.

¿Qué pareja de números al ser sumados su resultado es igual a 100 negativo?
Podría haber varias parejas de números que cumplan con esa condición, es decir, podría haber varias parejas de números, por ejemplo:
Si sumas:
-10 – 90 = -100
-75 – 25 = -100
-44 – 66 = -100
Puedes encontrar muchas combinaciones de pares de números que al ser sumados te den como resultado 100 negativo. Sin embargo, también es necesario que ese par de números al multiplicarse den como resultado el valor de “c”, que en este caso es 2500.
Si obtienes el producto de los pares de números que se mencionaron con anterioridad, quedaría de la siguiente manera:

Y como podrás darte cuenta, ninguno da como resultado 2500.
Tomando en cuenta los valores anteriores, ¿cuáles son esos dos números cuya suma sea el valor de b (-100) y como producto el valor que corresponde a c (+2500)?
Efectivamente, los números que al sumarse dan como resultado 100 negativo y al multiplicarse dan como resultado 2500 son: 50 negativo y 50 negativo, porque:
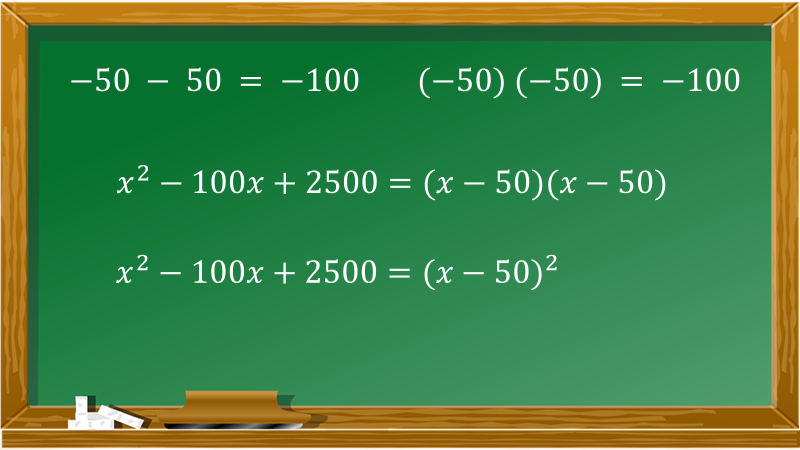
Con lo obtenido no resuelves el problema, ¿cuál es el área de los condominios y de los espacios verdes?
¿Qué valor no has utilizado? Efectivamente 1225, porque la ecuación se iguala a este valor. Para resolver este problema utilizarás la factorización de la siguiente forma:
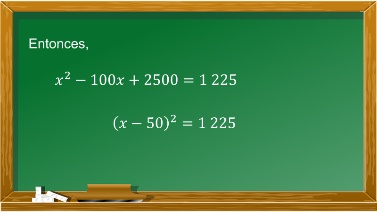
El producto de la diferencia de dos binomios se puede expresar como un binomio al cuadrado:
(x – 50) (x – 50)=(x-50)2
Por lo que el binomio al cuadrado se iguala a 1225: (x-50)2 = 1225
Como te diste cuenta en la expresión anterior (x-50) ^2 = 1225, la factorización que es otra forma de escribir la ecuación x^2 – 100x + 2500, se iguala al valor 1225 y con esto podrás calcular las diferentes áreas del terreno.
Ahora resuelve la ecuación que construiste para calcular cuántos metros cuadrados tendrán cada sección. Para resolver la ecuación primero hay que despejar la incógnita. Para esto empieza quitando el cuadrado, empleando la operación inversa de éste, es decir, la raíz cuadrada, pero para conservar la igualdad, debes aplicarla en ambos miembros de la ecuación.

Raíz cuadrada de (x – 50) ^2 = raíz cuadrada de 1225.
Realizando operaciones obtienes:
El cuadrado del binomio se cancela con la raíz cuadrada.
La raíz cuadrada de 1225 es 35 y queda: x – 50 = más-menos 35, recuerda que la raíz cuadrada de un número puede ser positivo o negativo.
Calculando los valores:
Para despejar “x”, se suma 50 a cada miembro de la ecuación para mantener la igualdad.
Para x1:
x – 50 + 50 = 50 + 35 y obtienes el valor para x1
x2 = 85.
Para x2:
x – 50 + 50 = 50 – 35
y obtienes el valor para x2
x2 = 15
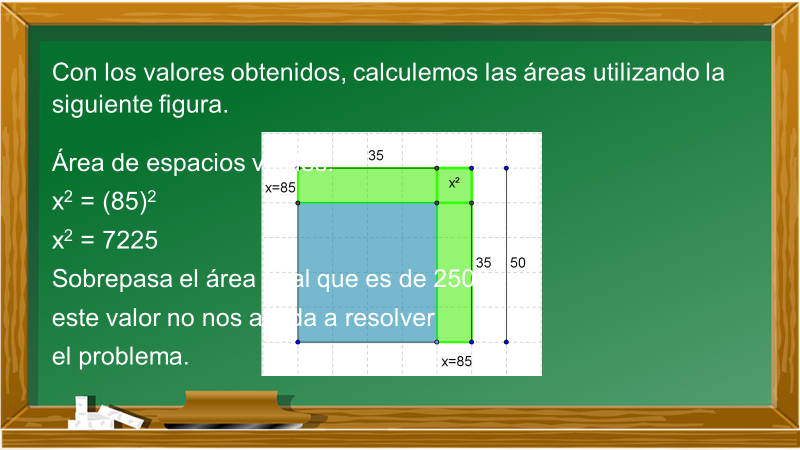
Utiliza el valor x1 = 85 y los sustituyes en las diferentes áreas de la figura.
Área de espacios verdes.
x^2 = (85) ^2
x^2 = 7225
Como puedes observar, al calcular el valor de x = 85, sobrepasa el área total, que es de 2500, esto quiere decir que este valor no ayuda a resolver el problema.
Utilizarás el valor de x2 = 15.
Área de espacios verdes:
x^2 = (15) ^2
x^2 = 225
Área de los 2 rectángulos:
(x) (35) = (15) (35) = 525
(2) (525) =1050
Sumas áreas verdes:
225 + 1050 = 1275
Área para condominios:
(35) (35) = 1225.
Con estos valores resuelves el problema, calculando las dos áreas.
Áreas verdes tienen un área de 1275 ucuadradas.
Áreas para condominios 1225 u cuadradas.
Sumadas dan un total de 2500 u cuadradas.
Ya aprendiste a utilizar método de factorización de un binomio al cuadrado.
El reto de hoy:
Para resolver dudas o ejercitar lo aprendido te puedes apoyar en tu libro de texto, en la página de Internet de Telesecundaria o cuando regreses a tu plantel pedir asesoría a tu profesor.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: