Construcción de polígonos regulares

Viernes

25

de noviembre

Segundo de Secundaria

Matemáticas

Construcción de polígonos regulares

Aprendizaje esperado: deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares.

Énfasis: resolver problemas de construcción de polígonos regulares con instrumentos geométricos a partir de varios datos.

¿Qué vamos a aprender?

Profundizarás en la resolución de problemas a partir de la construcción de polígonos regulares, utilizando instrumentos geométricos. Además, conocerás cómo localizar el centro de un pentágono usando mediatrices de los lados y bisectrices de los ángulos.

¿Qué hacemos?

Analizarás la siguiente situación:

En la clase de Formación Cívica y Ética, la maestra les pidió a sus alumnos elaborar un proyecto que consiste en identificar en cada miembro de su familia un valor universal o una cualidad que los caracterice, y entregárselos como reconocimiento. Para ello, cada estudiante entregará tarjetas en forma de polígonos regulares que incluyan al centro el valor que los caracterice.

Problema José

José, un estudiante de segundo de secundaria, pretende construir triángulos equiláteros de 10 centímetros de lado para este proyecto.

¿Cómo puede José construir cada uno de esos triángulos equiláteros con el uso de regla y compás?

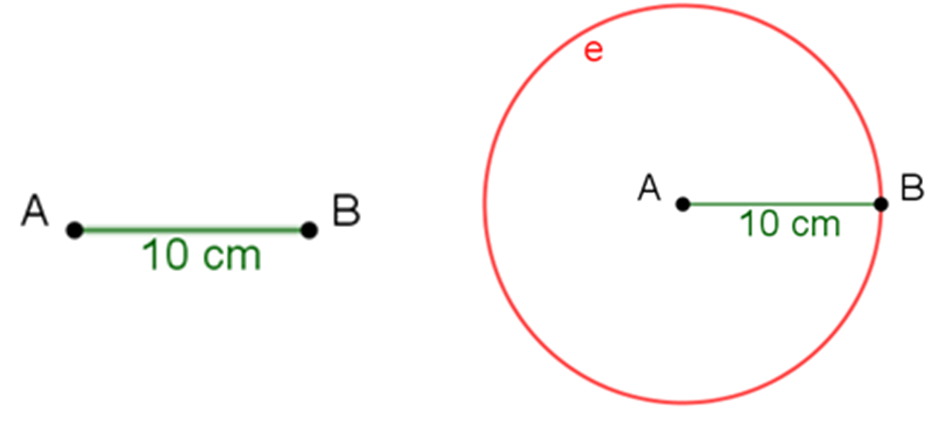
Ahora, constrúyelo. Traza un segmento de recta A-B que mida 10 cm.

Se sabe que los lados del triángulo deben ser iguales.

¿Cómo puedes asegurarte de que todos los lados tengan la misma longitud?

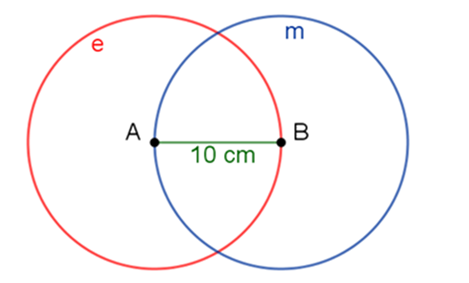
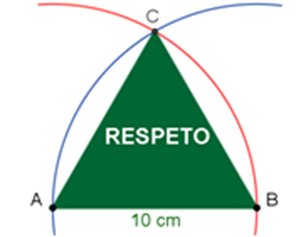
Usa el compás. Abre el compás a una longitud de 10 centímetros y traza la circunferencia “e”, tomando como centro el punto A del segmento A-B.

De esta forma, cualquier segmento que vaya de un punto de la circunferencia “e” hasta el punto A, tendrá una longitud de 10 centímetros. Asimismo, al trazar la circunferencia “m” de 10 centímetros de radio con centro en el punto B, cualquier punto de ésta, también tendrá una longitud de 10 cm hacia el punto B.

Observa que en el punto de intersección C de las circunferencias “e” y “m”, sus radios son de 10 cm.

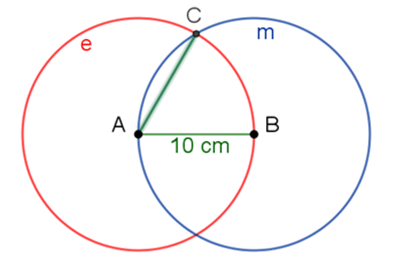
Al trazar los segmentos C-A y C-B, has construido el triángulo equilátero de 10 centímetros de lado.

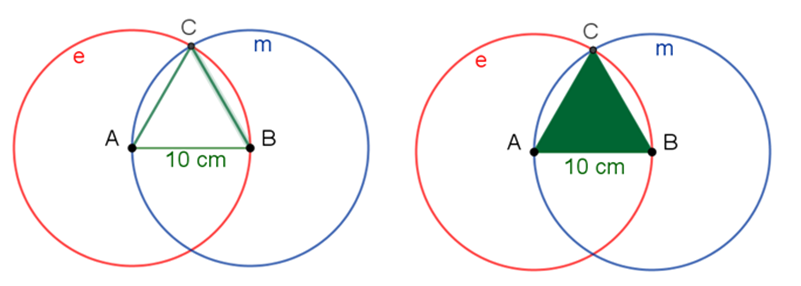
Ahora sólo le falta a José recortarlo e incluir la leyenda de un valor que caracterice a cada miembro de su familia. Él decidió anotar, para su mamá, “el respeto”, ya que ella es muy respetuosa y le ha inculcado a José el respeto a los demás y a sí mismo.

Problema Ana

Ana, por su parte, quiere usar cuadrados inscritos en una circunferencia de 6 cm de radio.

Los compañeros de clase le han propuesto que utilice las diagonales en la construcción de sus cuadrados.

¿Cómo puedes trazar las diagonales usando sólo regla y compás?

Realiza la construcción de Ana.

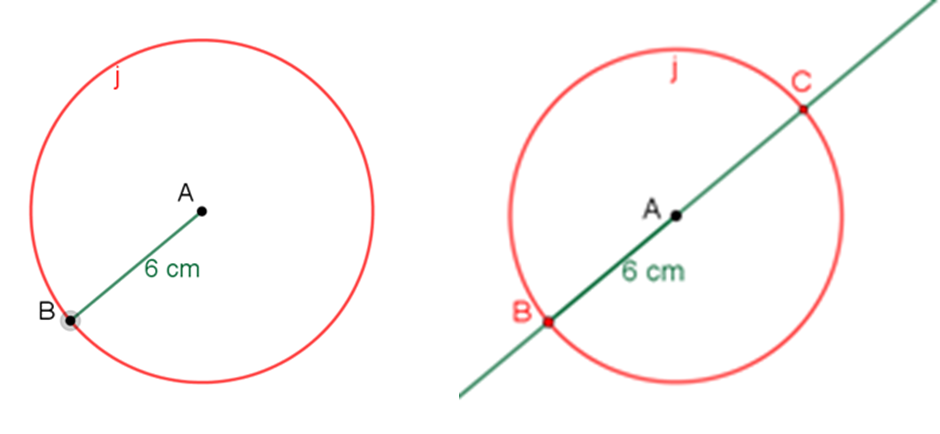
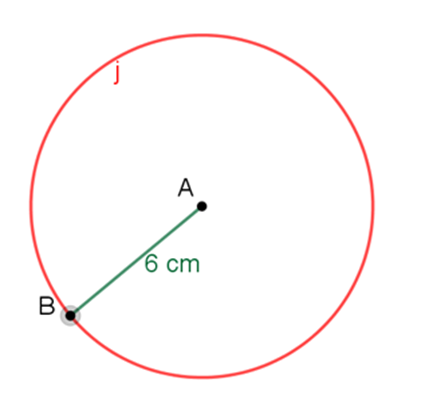
Se traza la circunferencia “j” de 6 centímetros de radio, tomando como centro al punto A. Después, se toma un punto cualquiera de la circunferencia “j” y llamado B.

Si B será un vértice del cuadrado, ¿cómo puedes trazar las diagonales usando sólo regla y compás?

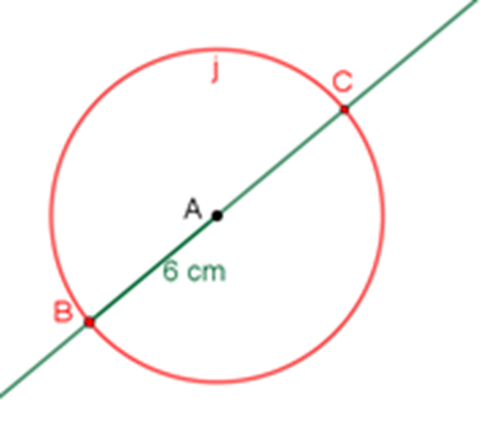
Al prolongar el segmento A-B de forma que interseque a la circunferencia “j” en el punto C, hallarás una de las diagonales del cuadrado, que es ahora el segmento B-C.

¿Cómo se traza la otra diagonal con regla y compás?

Traza la mediatriz del segmento B-C. Recuerda que la mediatriz es una recta perpendicular a un segmento y, además, pasa por su punto medio. En este caso, la mediatriz debe ser perpendicular a B-C y pasar por el punto A, que es el centro de la circunferencia “j” y el punto medio del segmento B-C.

Para trazar la mediatriz del segmento B-C, primero traza la circunferencia “m” abriendo el compás a un radio de 12 centímetros, tomando como centro el punto B.

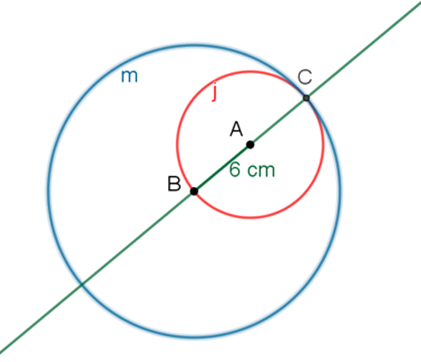
Después, traza la circunferencia “d”, abriendo el compás a un radio de 12 centímetros, tomando como centro el punto C.

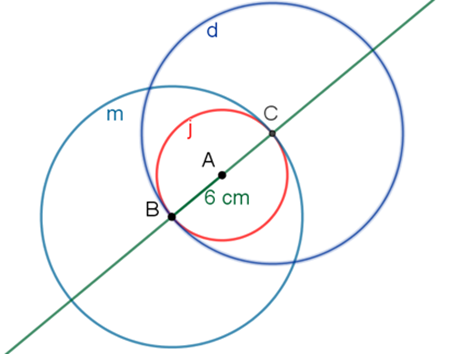
Las circunferencias “m” y “d” se intersecan en los puntos D y E por donde pasará la mediatriz de B-C.

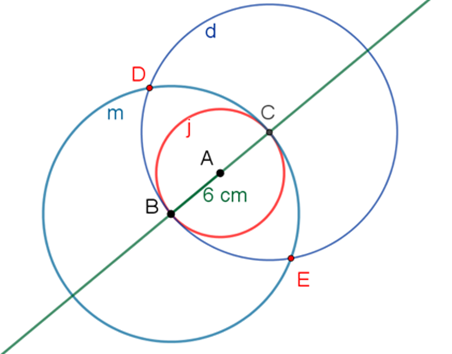
Al trazar el segmento D-E, te darás cuenta de que éste forma parte de la mediatriz del segmento B-C.

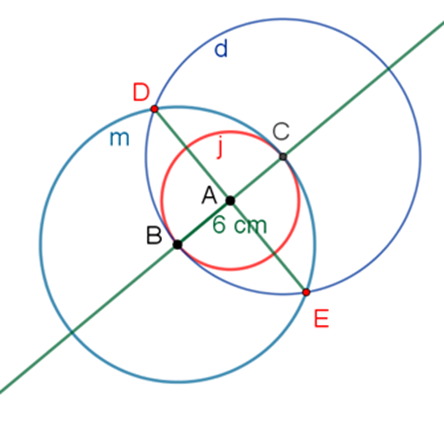
Las intersecciones del segmento D-E, con la circunferencia “j”, es decir, los puntos F y G, serán también vértices del cuadrado inscrito en la circunferencia “j”.

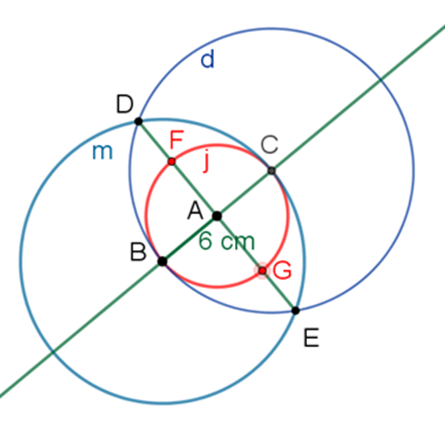
Al trazar los segmentos B-F, F-C, C-G y G-B, se forma el cuadrado de Ana.

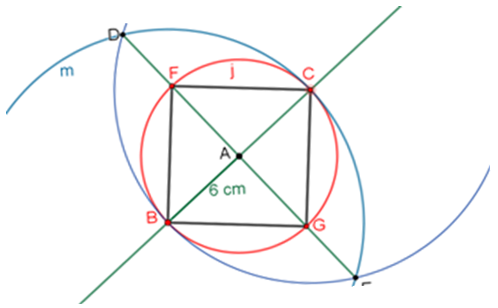
Puedes darte cuenta en el cuadrado de Ana que la longitud de cada lado es mayor que la longitud del radio.

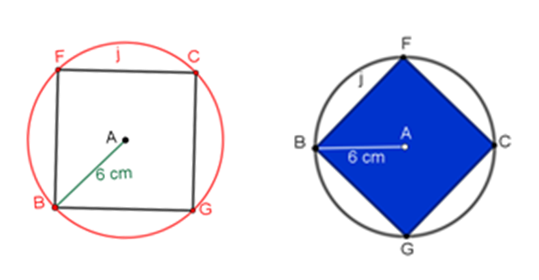
Finalmente, sólo falta que Ana lo recorte y anote el valor o la cualidad que reconoce en cada miembro de su familia. Ella identifica en su papá la justicia, anotándolo en el cuadrado.

Cada integrante del grupo de José y de Ana eligieron diferente polígono regular para su proyecto y diferentes formas para trazarlos.

Problema Luisa

Luisa optó por construir pentágonos regulares de 10 cm de lado.

¿Cómo puedes trazar un pentágono de 10 cm de lado?

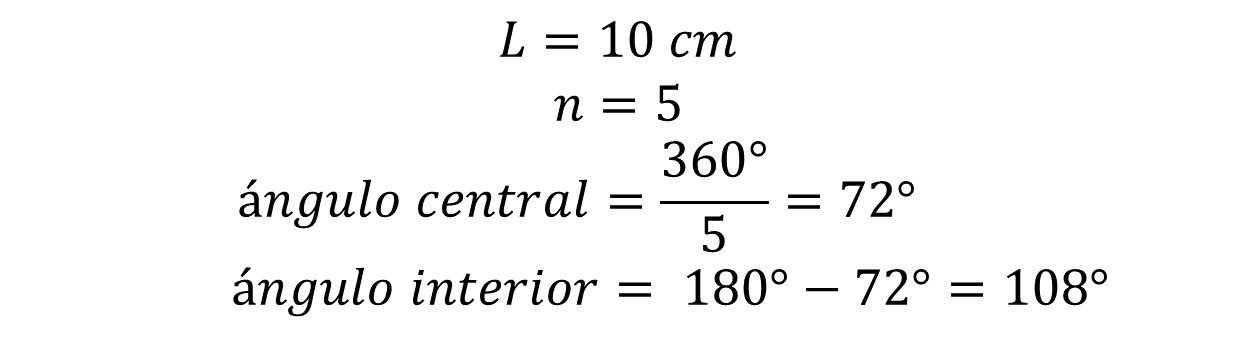
Ayúdale a Luisa a trazar su pentágono. Primero, examina:

¿Cómo puedes trazar un pentágono de 10 centímetros de lado?

Elige, ya sea el ángulo interior o el ángulo exterior.

Un pentágono tiene 5 lados y su ángulo central se obtiene al dividir 360 grados entre 5, es decir, 72 grados. Para encontrar el ángulo interior, a 180 grados se le restan 72 grados, porque son suplementarios, y se obtienen 108 grados.

Ahora, elige el ángulo interior.

Comienza a trazar el segmento A-B de 10 centímetros.

Ahora, usando el transportador, mide un ángulo interior de 108 grados sobre el segmento A-B utilizando como centro o vértice el punto A, y traza una semirrecta para formar ese ángulo.

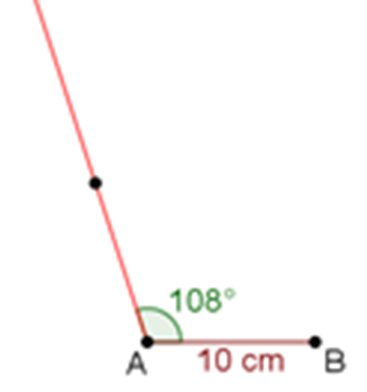
Para asegurarte de que el lado tenga igual longitud que el lado AB, abre el compás a 10 centímetros y marca la circunferencia “c”, considerando como centro el vértice A. La intersección de la circunferencia “c” con la semirrecta indica el tercer vértice del pentágono, este es el vértice E.

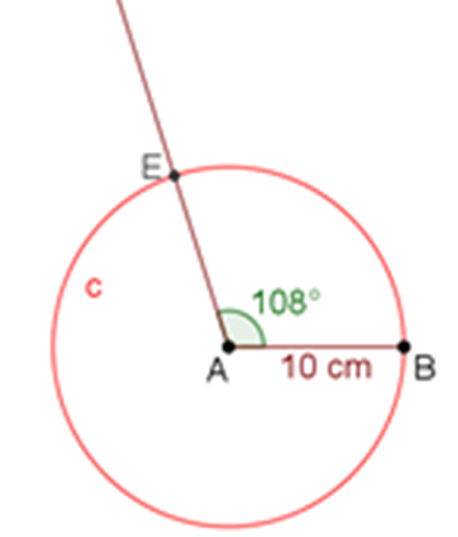
¿Cómo se pueden trazar los vértices C y D que faltan para completar el pentágono?

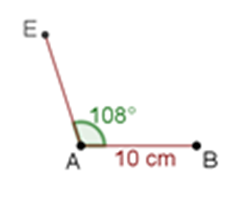
Continúa con el mismo procedimiento, midiendo cada uno de los ángulos interiores, para encontrar el punto D. Mide sobre el vértice E el ángulo interior de 108 grados, traza la semirrecta y localiza el vértice D.

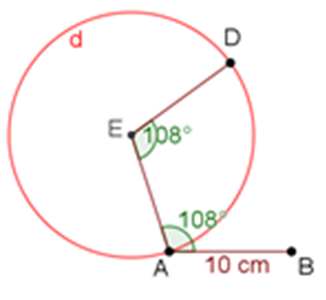
Para hallar el punto C, usa el compás, abriéndolo a una longitud de 10 centímetros, marcando las circunferencias “p” y “k”, tomando como centro los puntos D y B, respectivamente.

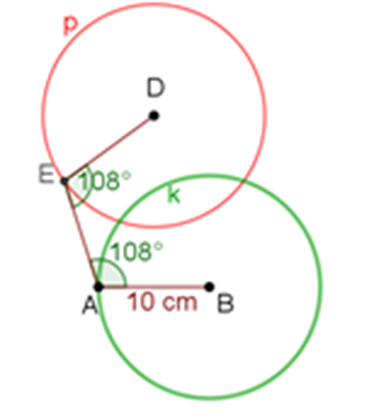
El punto C corresponde a una de las intersecciones de las circunferencias “p” y “k”.

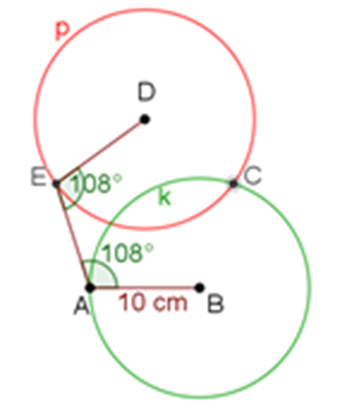
Una vez localizado el punto C, traza los segmentos D-C y C-B para terminar la construcción del pentágono.

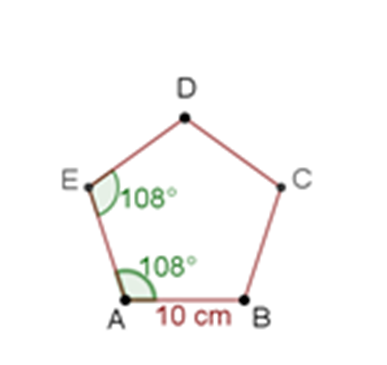
Has concluido la construcción del pentágono regular. Ahora, a Luisa se le ha ocurrido construir rehiletes en lugar de tarjetas para regalárselos a sus familiares.

Los rehiletes son juguetes compuestos por una varilla de madera que, en la parte superior, tienen sujeta al centro una figura de papel, celofán, cartón o cualquier otro material ligero, que gira con el viento. Esta figura será un pentágono regular en el caso de Luisa.

¿Cómo puedes encontrar el centro del pentágono?

Con el punto de intersección de las bisectrices de dos ángulos interiores se puede encontrar el centro. Luisa considera que es mejor trazando dos de las mediatrices de los lados del pentágono.

Traza las mediatrices de los segmentos D-E y D-C.

Primero, para trazar la mediatriz del segmento D-E, marca las circunferencias “e” y “q”, de 10 centímetros de radio, tomando como centro el vértice E y después el vértice D. Traza la mediatriz “m” que pasa por los puntos H y G, que son las intersecciones de las circunferencias “e” y “q”.

Mediatriz del DE

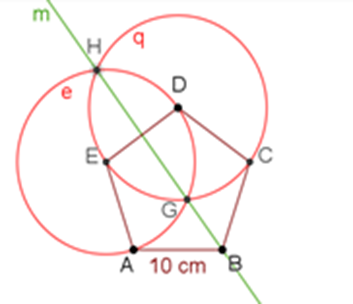
Ahora, traza la mediatriz del segmento D-C. Para ello, marca las circunferencias “q” y “r”, de 10 centímetros de radio, tomando como centro los vértices D y C. Localiza sus intersecciones correspondientes, que son los puntos “j” y “k”, y traza la mediatriz “n” que pasa por los puntos “j” y “k”.

Mediatriz del DC

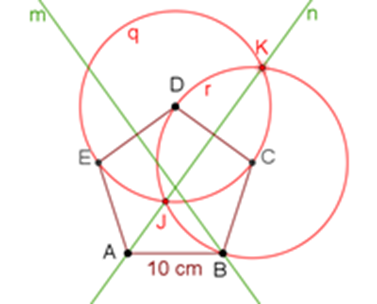
Luisa asegura que el punto de intersección de las mediatrices “m” y “n” es el centro del pentágono O.

Punto de intersección O

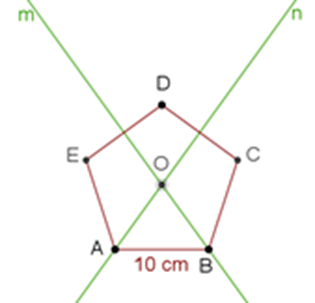
¿Cómo se puede asegurar de que el punto O es el centro del pentágono?

Traza la circunferencia circunscrita del pentágono tomando como centro el punto O. La circunferencia circunscrita “s” debe intersecar a todos los vértices del pentágono.

Circunferencia circunscrita “s”

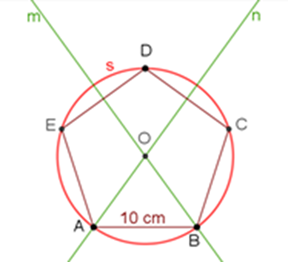
Al abrir el compás desde el centro O hasta el vértice A y trazar la circunferencia “s”, ésta cruza a todos los vértices del pentágono. También, la longitud de un lado es mayor que la longitud del radio.

Luisa ha podido trazar un pentágono regular de 10 centímetros de lado usando el ángulo interior para ello.

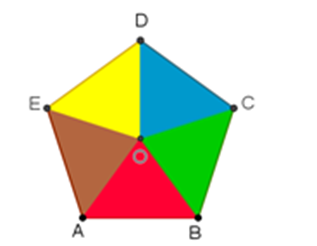
Además, encontró el centro del pentágono para poder construir un rehilete pentagonal usando las mediatrices de los lados D-E y C-D.

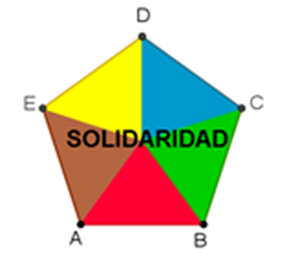
Luisa decidió regalarle uno de los reguiletes pentagonales que construyó a su amigo Pedro con la leyenda de solidaridad, porque él siempre la apoya en sus clases.

Problema Pedro

Pedro se ha quedado intrigado de saber si puede encontrar el centro del pentágono.

• Utilizando las bisectrices de los ángulos A y B.
• La bisectriz es la recta que divide un ángulo en dos ángulos iguales.

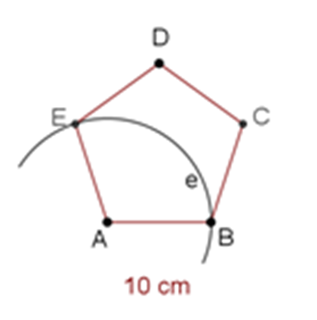
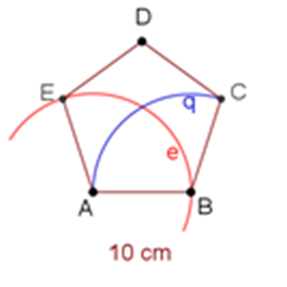
Para trazar la bisectriz del ángulo A, Pedro traza el arco “e”, con una abertura del compás de 10 centímetros, tomando como centro el punto A, de tal forma que interseque a los vértices E y B.

Arco “e”

Con esa misma abertura del compás, ahora tomando como centro el punto B, traza el arco q.

Arco “q”

Después, apoyándote en el punto E, con la misma abertura del compás, traza el arco “r”.

Arco “r”

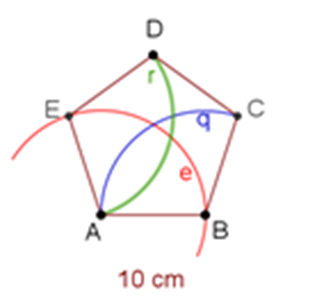
Traza la recta que pasa por los puntos de intersección de los arcos “r” y “q”, es decir, traza la bisectriz “y” del ángulo A.

Bisectriz “y” del ángulo A

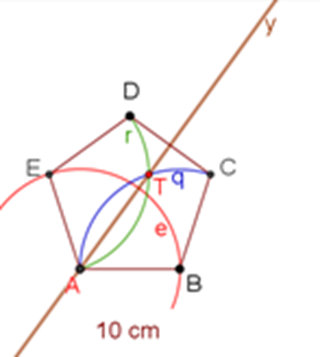
Repite este procedimiento para marcar la bisectriz del ángulo B.

Bisectriz “x” del ángulo B

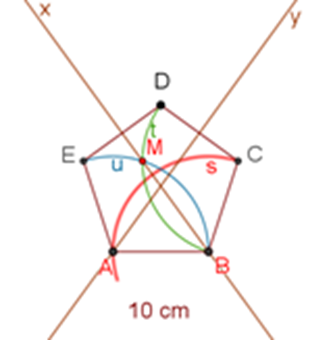
Marca el arco “s”, de 10 centímetros, intersecando a los vértices A y C del pentágono, tomando como centro el punto B. Con la misma abertura del compás de 10 centímetros, tomando como centro al vértice C, traza el arco “t” desde el vértice “D” hasta el vértice “B”. De la misma forma y con la misma abertura del compás de 10 centímetros, tomando como centro al vértice A, traza el arco “u” desde el vértice “E” hasta el vértice “B”. Posteriormente, traza la bisectriz “x” del ángulo B marcando la recta que pasa por los puntos de intersección de los arcos “t” y “u”.

Pedro asegura que el centro del pentágono O es el punto de intersección de las bisectrices “x” y “y”.

Para comprobarlo, Pedro marca la circunferencia circunscrita del pentágono y ésta, en efecto, interseca a todos los vértices del pentágono.

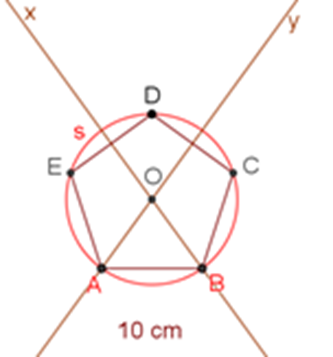
Pedro y Luisa han realizado dos construcciones diferentes para encontrar el centro del pentágono.

Analiza ambos trazos para el pentágono.

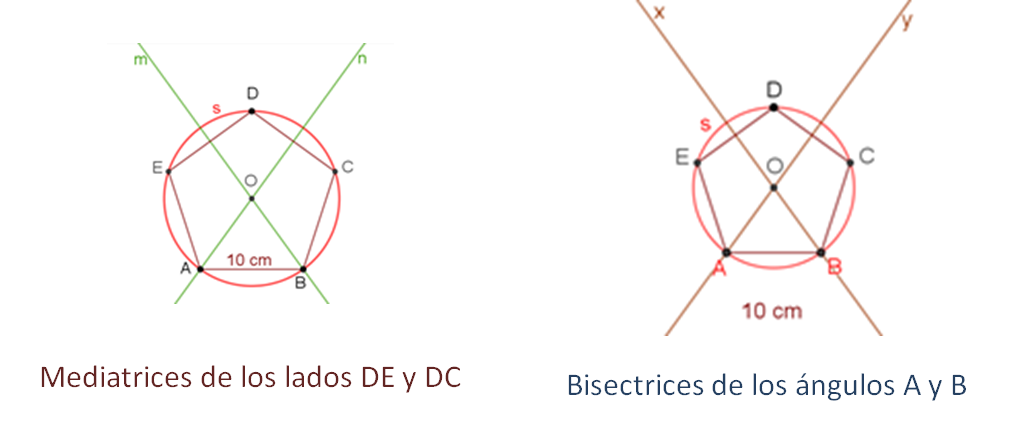
¿Cómo son las mediatrices de los lados DE y DC al compararlas con las bisectrices de los ángulos A y B?

• La mediatriz “m” del segmento (DE) corresponde a la bisectriz “x” del ángulo B.
• La mediatriz “n” del segmento (DC) corresponde a la bisectriz y del ángulo A.

Problema Arturo

Arturo ha decidido, para este proyecto, construir hexágonos regulares. Arturo recibe diferentes recomendaciones de sus compañeras y compañeros para la construcción de los hexágonos.

• José dice que puede trazar seis triángulos equiláteros.
• Ana le indica que puede usar sus diagonales.
• Luisa le recomienda usar uno de sus ángulos interiores.
• Pedro asegura que puede trazarlo usando el ángulo exterior.

¿Cómo se puede trazar un hexágono regular de 8 centímetros de lado?

Arturo decide construir su hexágono regular utilizando el ángulo exterior y corroborar quién de sus compañeros tiene razón.

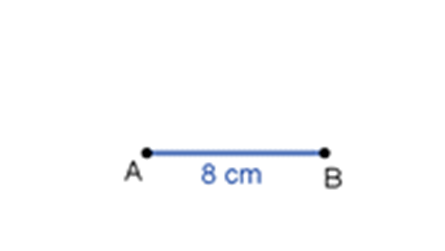
Para construirlo, traza el segmento de recta A-B de 8 cm.

El ángulo exterior es de 60 grados, prolonga el segmento A-B para medir con un transportador el ángulo exterior de 60 grados, considerando el punto B como vértice.

Ahora mide el ángulo exterior de 60 grados y marca una semirrecta del punto B al punto P que marcó con el transportador.

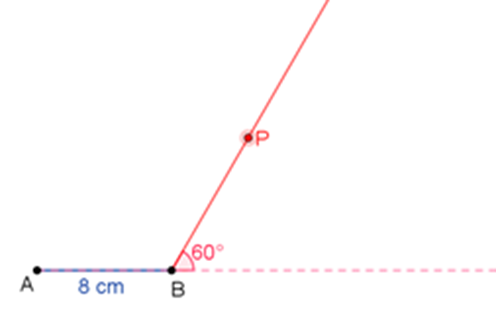
¿Qué debe hacer Arturo para que el lado que pasará por la semirrecta BP mida también 8 centímetros?

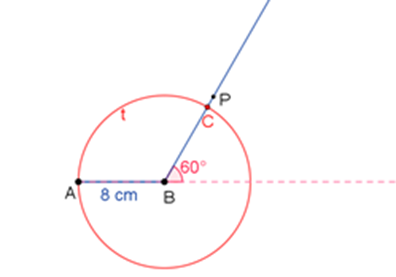
Ahora, usa el compás a una abertura de 8 centímetros y, tomando como centro el vértice B, traza la circunferencia “t” de forma que interseque a la semirrecta B-P en el punto C.

Verifica que el ángulo interior A-B-C sea de 120 grados.

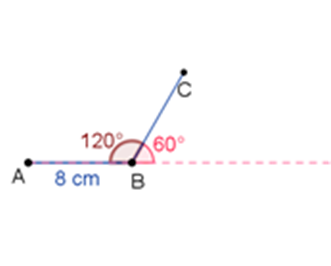
¿Cuáles son los siguientes trazos que debe hacer Arturo para completar su hexágono?

Encontrar el centro del hexágono, ya que, con dos de sus lados al trazar sus mediatrices, se puede encontrar el centro y, con él, encontrar sus vértices.

Mediatrices de los segmentos AB y BC

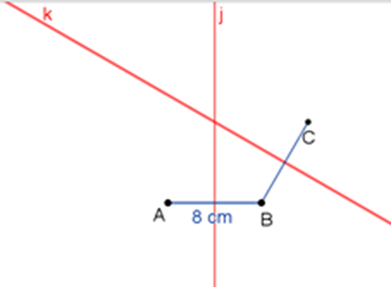
Traza las mediatrices de los segmentos A-B y B-C. En el punto de intersección de las mediatrices “j” y “k” se localiza el centro del hexágono. Posteriormente, traza la circunferencia “m”, ya que los vértices del hexágono intersecan esa circunferencia.

Circunferencia “m”

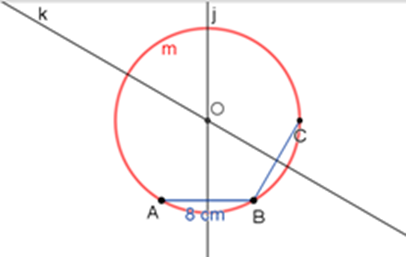
¿Cómo puede Arturo localizar los vértices D, E y F para terminar de construir el hexágono?

Se abre el compás con una abertura de 8 centímetros y, tomando como centro el punto C, traza la circunferencia U intersecando a la circunferencia “m” en los puntos B y D.

Circunferencia “u”

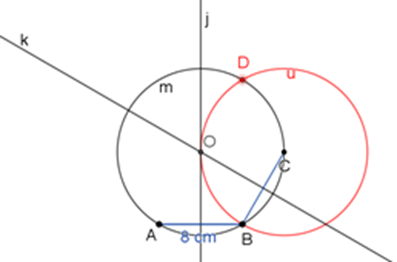
Reflexiona:

¿Por qué la circunferencia “u” también coincide con el centro del hexágono?

Esto quiere decir que el radio de esa circunferencia también mide 8 centímetros.

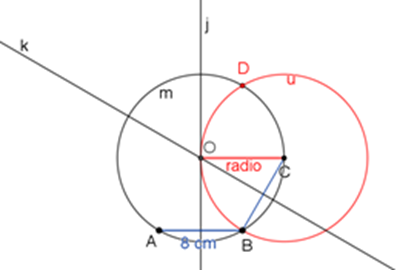
Se comprueba que, en efecto, el hexágono está formado por triángulos equiláteros porque el radio es igual al lado del hexágono.

Para proseguir los trazos del hexágono, continúa trazando el segmento D-C.

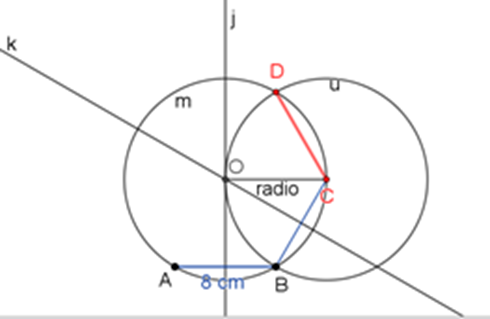
Posteriormente, para localizar el vértice F, marca la circunferencia “v” con una abertura de 8 centímetros, tomando como centro el punto A.

Circunferencia “v”

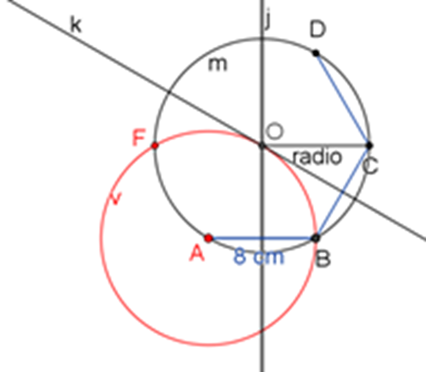
El punto de intersección de la circunferencia “v” con la circunferencia “m”, le llama vértice F. Traza un segmento de recta desde el punto A hasta el punto F.

Segmento de AF

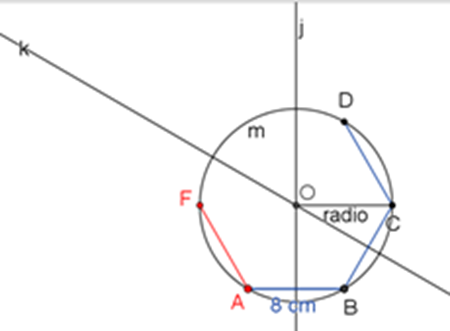
Finalmente, traza la circunferencia “e”, tomando como centro el punto D, con una abertura del compás de 8 centímetros.

Segmento de DE

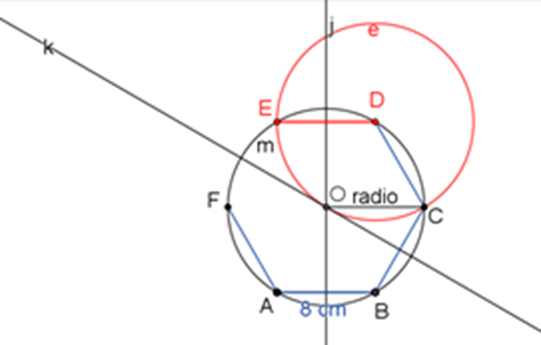
El punto de intersección de las circunferencias “e” y “m”, lo denomina el vértice E. Después marca el segmento E-F para terminar el trazo.

Segmento de EF

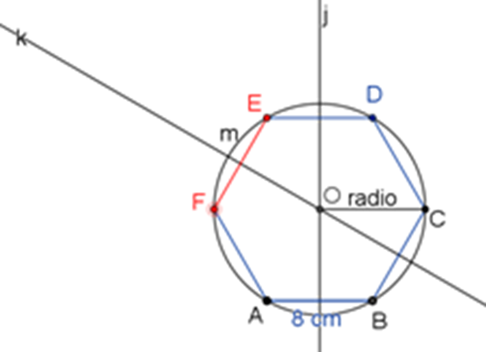
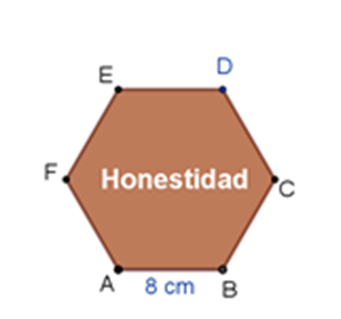
Una vez que Arturo terminó de construir el hexágono, consideró que era importante reconocerle a su hermano el valor de la honestidad.

Reflexiona acerca de las construcciones que se han realizado.

Analiza los trazos del pentágono y del hexágono.

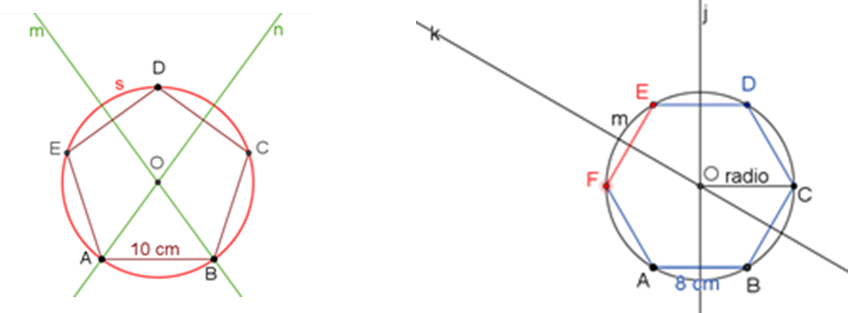
La mediatriz de un lado en un polígono regular, ¿siempre interseca a uno de sus vértices?

Se puede predecir en qué polígonos regulares las mediatrices intersecan a los vértices. La mediatriz “m” del pentágono interseca al vértice B, así como la mediatriz “n” interseca al vértice A. Pero esto no ocurre en el hexágono, la mediatriz “j” del segmento E-D también es la mediatriz del segmento A-B, así como la mediatriz del segmento E-F también es mediatriz del segmento B-C y no pasan por ningún vértice.

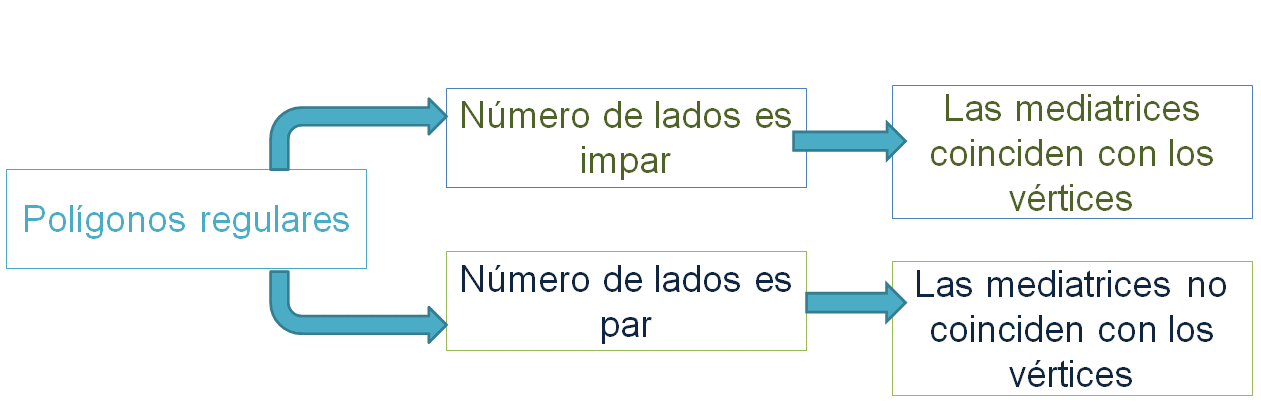
En polígonos regulares, cuando el número de lados es par, las mediatrices de los lados no coincidirán con alguno de los vértices. Asimismo, las mediatrices de los lados de un polígono regular coincidirán con algunos de sus vértices cuando el número de lados es impar.

Por lo tanto, se puede construir un polígono regular utilizando diferentes datos, como la longitud del lado del polígono regular, el ángulo interior o el ángulo exterior.

También has encontrado el centro de algunos polígonos regulares usando la mediatriz en un caso, o la bisectriz en otro.

Ahora reflexiona en qué otras situaciones puedes utilizar estas construcciones.

En la clase de Ciencias con énfasis en Física, el maestro solicitó un proyecto de óptica relacionado con la luz. Uno de los equipos encontró el disco de Newton y quiere construirlo.

Newton quería demostrar que la luz se descomponía en los colores del arcoíris.

El disco de Newton es un dispositivo circular dividido en siete sectores circulares con los siete colores fundamentales del arcoíris, que al girar se combinan para formar el color blanco.

Observa cómo la resolvieron algunos alumnos.

Araceli, una de las integrantes del equipo, decide trazar a la circunferencia “s” de 15 centímetros de radio en una cartulina blanca.

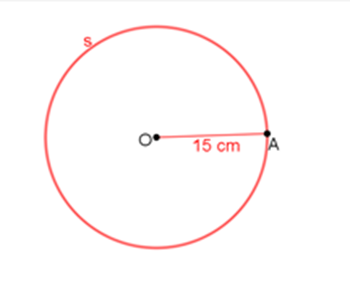
Reflexiona:

¿Cómo se divide el círculo en siete sectores iguales?

Para calcular el ángulo central, se divide 360 grados entre 7, que es aproximadamente 51.43 grados, esto quiere decir que la medición será aproximada.

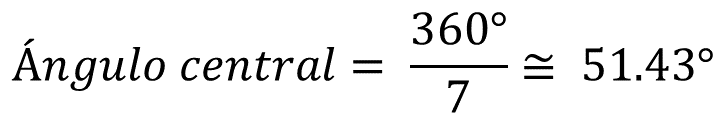
Araceli mide el ángulo central de aproximadamente 51.4 grados con el transportador marcando los radios A-O y B-O que lo forman.

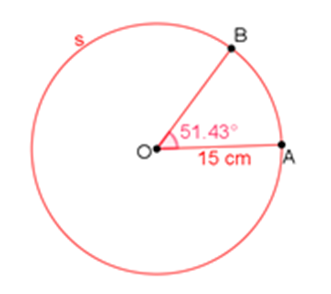
Después, con el compás mide la abertura desde el punto B hasta el punto A. Con esa abertura, tomando como centro el punto B, marca un arco de forma que interseque a la circunferencia “s” en el punto C.

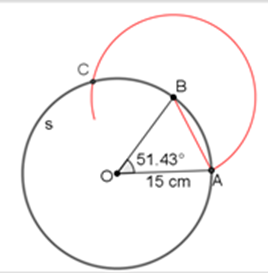
Repite este procedimiento hasta llegar al punto A sin modificar la abertura del compás.

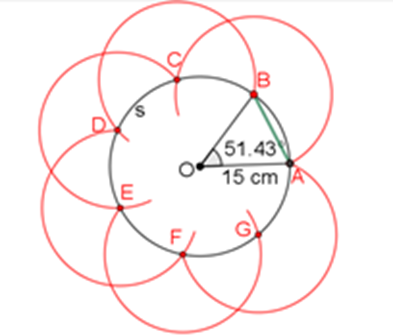
Marco traza los radios O-C, O-D, O-E, O-F y O-G.

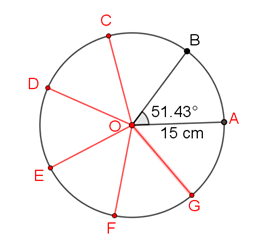
Es tiempo de colorear de acuerdo con el orden de los colores del arcoíris: rojo, naranja, amarillo, verde, cian, azul y violeta.

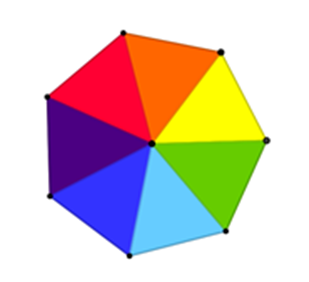
Ahora, en el centro del heptágono, coloca un hilo de cáñamo (también puede ser un pedazo de estambre), de forma que al girarlo en un sentido y estirarlo, éste gire rápidamente en sentido contrario.

¡Haz tu propio disco de Newton y verifica lo que sucede!

Recapitulando, en esta sesión:

• Se construyó un triángulo equilátero con regla y compás.
• Elaboraste un cuadrado inscrito en una circunferencia usando sus dos diagonales.
• Construiste un pentágono regular usando su ángulo interior.
• Localizaste el centro de un pentágono regular usando las mediatrices de los lados.
• También se localizó el centro de un pentágono regular trazando las bisectrices de sus ángulos.
• Aprendiste que, en un polígono regular de número de lados impar, la bisectriz de un ángulo corresponde a la mediatriz de uno de sus lados.
• Se construyó un hexágono regular usando el ángulo exterior y un heptágono usando el ángulo central.

Recuerda que este es un material de apoyo y puedes consultar otras fuentes para complementar lo que aprendas aquí.

El reto de hoy:

Construye un octágono regular inscrito en una circunferencia de 10 cm de radio y un eneágono regular de 10 cm de lado, usando el ángulo exterior, y localiza su centro.

Después describe el procedimiento de construcción de cada polígono.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/