Construcción de gráficas circulares
Aprendizaje esperado: recolecta, registra y lee datos en gráficas circulares
Énfasis: construir gráficas circulares a partir de recolectar y registrar información en tabla (frecuencias absolutas).
¿Qué vamos a aprender?
Obtener información, organizarla y estudiarla es también un aspecto del que se encargan las matemáticas. Y en esta sesión se hablará del gráfico circular, también conocido como gráfico de sectores o en un ambiente más coloquial, gráfica de Pastel.
Se le conoce como gráfica de pastel porque asemeja a un pastel rebanado en diferentes partes. No olvides que para tomar la sesión y no perder detalles debes tener a la mano:
Tu cuaderno de la asignatura, o en su defecto hojas de reúso, lápiz, goma, compás, un transportador y colores.
¿Qué hacemos?
Cuando puedes acceder a datos de un objeto de estudio en específico, la organización y presentación de estos te brindan una gran oportunidad de conocer y entender de mejor manera su funcionamiento.
Por ejemplo, en la mercadotecnia, al elaborar una encuesta o al tener el registro de ventas, se puede tener un mejor análisis al ordenar la información.
Y como ya sabes, la rama de las matemáticas que se dedica al estudio, organización y análisis de datos es la estadística. En esta sesión te enfocarás en la gráfica circular.
¿Qué elementos consideras que son indispensables para construir una gráfica circular?
Observa la siguiente imagen.
Imagina tener esta gráfica circular, muy colorida, pero no muestra ninguna información.
Las gráficas por si mismas brindan información sobre alguna situación, pero es necesario saber el objeto de estudio.
Ahora observa la siguiente imagen.
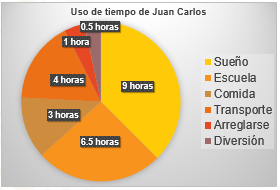
Ahora es más entendible, la gráfica trata del uso del tiempo de Juan Carlos, por los rótulos se observa que se tratan de horas y diferentes actividades como el sueño, la escuela, comida entre otras.
Esta gráfica muestra las actividades de Juan Carlos en un día, en ella se demuestra que la mayor parte de su tiempo está destinado al sueño y la escuela, en total estas dos actividades requieren 15.5 horas del día
Al sumar las horas de todas las actividades es 24, alumnas y alumnos si sumas las horas de la comida, transporte, arreglarse y diversión que es 3 + 4 + 1 + 0.5 se obtiene 8.5 horas y le añades los 15.5 del sueño con la escuela es 24 horas.
Es decir, la gráfica en su totalidad representa un día entero.
Muy buena observación, debes tener en cuenta que el total del estudio está representado por el círculo completo, es decir, en este caso particular este círculo representa las 24 horas del día. Ahora completa una tabla de datos con la información de la gráfica ya que esto ayudará a entender la forma que se sigue para la construcción de una gráfica circular.
Haz la tabla, de acuerdo a la gráfica puedes hacer dos columnas, en la primera anotarás la actividad, en la segunda las horas que marca la gráfica. La primer actividad es Sueño con 9 horas, después la escuela con 6.5, y la comida con 3 horas.
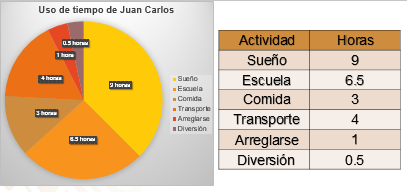
El transporte va con 4 horas, arreglarse con 1 y la diversión tiene 0.5 horas.
Si tienes en cuenta que es una circunferencia la que va a ser el modelo para la gráfica, hay que considerar que cada actividad debe ser representativa en su sector, de tal forma que la circunferencia completa equivalga a las 24 horas de un día, es decir, cada sector debe ser proporcional a la información que representa, en este caso, una hora debe ser la veinticuatroava parte del círculo.
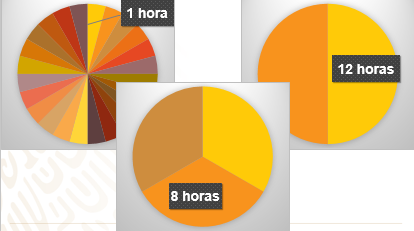
Por ejemplo 12 horas debe ser la mitad de la circunferencia o también 8 horas debe ser la tercera parte de la circunferencia.
Porque 8 es la tercera parte de 24. Y la forma más práctica para poder elaborar la gráfica circular sería utilizar el transportador.
Y se tienen que trazar los sectores de acuerdo con el ángulo que le corresponde, para conocer el ángulo puedes establecer un relación de proporcionalidad entre el total de los datos y los 360° que mide una circunferencia completa. Esto te ayudará a determinar la medida de cada uno de los sectores circulares que tendrá la gráfica.
Agrega otra columna a la tabla para poder establecer la medida de estos ángulos.
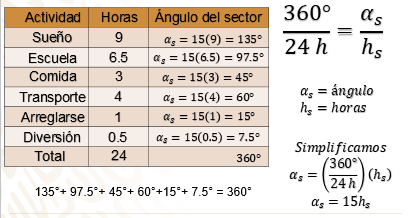
Para conocer la medida del ángulo se establece la proporción 360° sobre 24 h que es igual al ángulo del sector sobre las horas de la actividad. Simplifica y se tiene que el ángulo del sector correspondiente a una hora es igual a 15 grados, es decir, cada ángulo es 15 veces las horas de la actividad.
Entonces en cada caso multiplicarás el tiempo de cada actividad por 15, así para el sueño son 9 horas que al multiplicar por 15 es igual a 135, que representa la medida del ángulo correspondiente, 135 grados.
En la escuela invierte 6.5 horas y al multiplicar por 15 es igual a 97.5 grados.
Para la comida son 3 horas y al multiplicarlo por 15 obtienes el ángulo es de 45 grados.
En el transporte Juan Carlos emplea 4 horas. Multiplicas 4 por 15 y obtienes 60 grados.
En el concepto de arreglarse es 1 hora, lo multiplicas y queda un ángulo de 15°
En diversión únicamente es 0.5 horas y al multiplicar por 15 se queda con 7.5°
Ten en mente que la sumatoria de todos los ángulos de cada sector, deberá ser de 360°
Haz la suma para ratificar este valor:
135°+ 97.5°+ 45°+ 60°+15°+ 7.5° es igual a 360°
Esta tabla tan detallada permite saber cómo obtener la medida de los ángulos al construir una gráfica circula.
Este tipo de tablas que son comúnmente utilizadas en la estadística reciben el nombre de tabla de frecuencia.
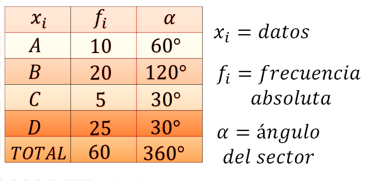
Ya que mayoritariamente se registra las veces que sucede algún objeto de estudio.
Las tablas de frecuencia incluyen básicamente los datos a estudiar representados por x subíndice “i”, frecuencia absoluta que se anota como f subíndice “i” e incluirás una columna con la medida del ángulo del sector circular, para poder construir las gráficas circulares.
¿Sobre qué podrías hacer una gráfica circular?
Se pueden estudiar muchas situaciones, pero no todas pueden ser abordadas mediante un gráfico circular. Piensa en la siguiente situación.
Pon atención y registra los datos que consideres importantes.
Miguel consiguió un permiso para vender en el carnaval de su comunidad por lo que ha decidido hacer una encuesta con amigos y personas en la comunidad para saber qué tipo de puesto le conviene poner.
Al agrupar los datos obtiene la cantidad de personas que prefieren asistir a un determinado tipo de puesto, estos son los resultados:
Canicas 95 personas, comida 125 personas, Aguas 62 personas, Globos 78 personas.
Parece que realizó la encuesta a varias personas, este tipo de datos puedes observarlos en una gráfica circular. Puedes hacer la tabla con 6 filas y 3 columnas:

La primera fila será de los encabezados, así sabrás de que trata cada columna. La primera será de los datos, que en este caso es el tipo de puesto y lo anotas como “x” subíndice “i”, la segunda columna será la frecuencia absoluta, de cada dato, y la representas como “f” subíndice “i” por último anotarás alfa, que representará la medida del ángulo del sector circular correspondiente.
A partir de la segunda fila anotarás el nombre del tipo de puesto que registró y la frecuencia absoluta, en este caso el orden en el que colocarás el tipo de puesto no es relevante, aunque se puede organizar anotando en primer lugar el que obtuvo mayor frecuencia
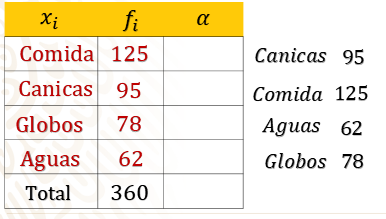
De los datos el que tiene mayor frecuencia es el puesto de comida con 125, después las canicas con 95, sigue el juego mecánico con 78 y por último 62 del agua.
De los datos el que tiene mayor frecuencia es el puesto de comida con 125, después las canicas con 95, sigue el juego mecánico con 78 y por último 62 del agua
La última fila será donde apuntes el total, que al hacer la suma se obtiene 360.
Esto es muy conveniente, ya que al ser en total 360 encuestados, al establecer la proporción con los 360° tendrías que cada encuestado representaría 1° en la gráfica.
Esto va a simplificar mucho el llenado de la siguiente sección de la tabla, que corresponde al ángulo del sector y así poder hacer nuestra gráfica circular:
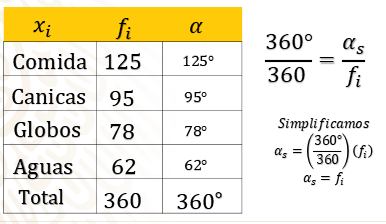
Para completar la tabla realiza la proporción directa 360° entre 360 que es igual al ángulo del sector entre la frecuencia absoluta. Puedes comprobar que lo que es cierto ya que al dividir 360° entre 360, el cociente es uno. Por lo que al despejar el ángulo del sector circular queda igual a la frecuencia absoluta.
Así entonces los sectores circulares serán de 125° para comida, 95° para la canica, 78° los globos y 62° las aguas, en total 360°
Ya tienes la medida de los ángulos, ahora para construir la gráfica circular, puedes trazar un círculo con un radio de 8 cm, y empezar a marcar los ángulos de cada sector.
Prepara tu compás y transportador ya que los utilizarás.
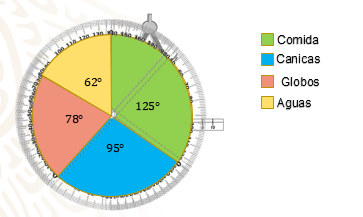
Primero traza la circunferencia y marca el radio como punto de referencia para trazar el primer ángulo que es de 125°, este sector lo colorearás y anotas el rotulo correspondiente. Ahí donde terminó el sector de la comida, alineas el trasportador y marcas el siguiente ángulo que corresponde a 95°, del puesto de las canicas, también coloreas el sector y anotas su rótulo. El procedimiento se va repitiendo, vuelves a posicionar el transportador donde finalizó el sector de las canicas y ahora marcarás 78 grados y sólo resta el sector de las aguas con 62 grados.
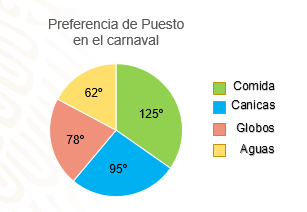
Ya tienes la gráfica circular de la encuesta realizada por Miguel, que refleja de forma clara cuál es la elección más alta en la encuesta que realizó. Así puede tomar una decisión más informada.
Aunque Miguel consideró que no tenía la suficiente información y quiso complementarla indagando sobre la cantidad de puestos que hay de cada uno. Y decidió hacer con los datos otra gráfica circular para comparar y así tomar su decisión.
Los datos que consiguió es la siguiente:
De Comida hay 12 puestos, de canicas son 18, de globos 15 puestos y aguas 3.
Con estos datos puedes hacer tu tabla, recuerda ordenarás las frecuencias de mayor a menor.
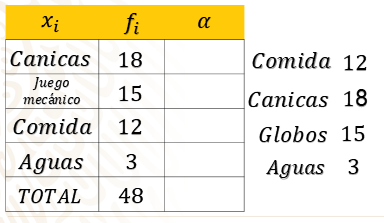
En primer lugar, están las canicas con 18 puestos, después los juegos mecánicos con 15 puestos, la comida con 12 le sigue y por último el puesto de agua con 3
Recuerda que se concluye esta columna sumando los valores de la cada una de las frecuencias absolutas, que en este caso es de 48 puestos en total.

Con la frecuencia absoluta anotada podemos comenzar a hacer el cálculo de la medida del ángulo del sector circular. Establecemos la proporción 360° sobre 48 igual al ángulo del sector sobre su frecuencia absoluta.
Al despejar el ángulo del sector queda el producto de 360° sobre 48 que multiplica a la frecuencia absoluta, obtenemos el cociente y obtienes 7.5, lo que significa que a cada puesto le corresponde un ángulo de 7.5 grados.
Así para las canicas multiplicas 7.5 por 18 obtienes 135 grados para el sector, para los globos el ángulo es de 112.5 grados; para la comida de 90 grados y finalizas para las aguas, de 22.5 grados.
Haces la suma de los ángulos obtenidos y se confirma que el total es 360 grados.
Ya tienes todo lo necesario para construir la gráfica circular.
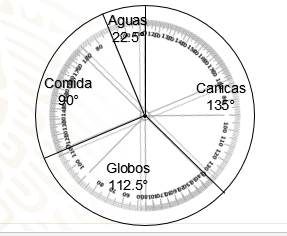
Como verás en la imagen ya tienes marcado el centro, la circunferencia y su radio. Vas a marcar los 135° de las canicas, después, marca un ángulo de 112.5°; prosigue con la comida cuyo sector es de 90° y el sector faltante corresponde a los puestos que habrá de agua.
Así como se muestra, puedes anotar los rótulos sobre su mismo sector circular, acompañado por la medida de ángulo.
Es muy importante lo que se menciona sobre los rótulos, ya que toda gráfica debe ser acompañada de los datos que dan origen a su construcción, de lo contrario podrías cometer errores de interpretación.
Miguel terminó sus gráficas y así es como le quedaron.
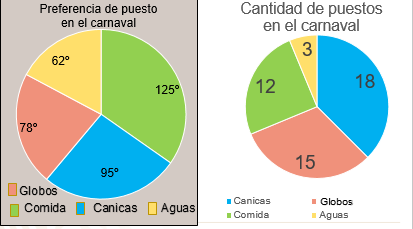
Como podrás observar, del lado izquierdo está la encuesta que realizó a personas de la comunidad sobre sus preferencias de compra al ir al carnaval, y en la segunda, la gráfica muestra la cantidad de puestos que se han puesto con anticipación en el carnaval.
Está muy bien el detalle en el que utilizó el mismo color en ambas gráficas y así puedes identificar y comparar más fácilmente la información.
Estos elementos son de suma importancia ya que, al ser un gráfico, los recursos visuales son de suma importancia. Pero falta responder la pregunta que está buscando Miguel,
¿Qué tipo de puesto le conviene poner?
Se puede decir que hay que buscar un elemento que tenga un sector grande del lado izquierdo pero pequeño del lado derecho, para que así tenga alta demanda y poca competencia.
Observa otro caso donde la gráfica circular fue de utilidad para el registro de datos.
Perla tiene a su cargo la cocina económica de su mamá, las ventas no han sido buenas y en ocasiones se ha quedado con los platillos que prepara para la comida. La cocina vende dos modalidades, la comida a la carta que es preparada al momento y la comida corrida que es un platillo diferente que se prepara con anticipación. A Perla le conviene vender la comida corrida, ya que así la atención es rápida y el costo de preparación se reduce. pero necesita preparar lo suficiente para que no se quede con comida. Durante una semana Perla llevó el registro de las ventas obteniendo la siguiente tabla de resultados
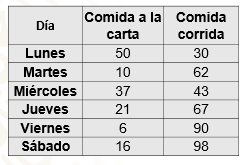
En la tabla que hizo Perla, en la primera columna anotó lo días de la semana, en la segunda columna correspondiente a la venta de la comida a la carta, los valores son, 50, 10, 37, 21, 6 y 16.
Para la tercera columna que representa la venta de comida corrida se registró, 30, 62, 43, 67, 90 y 98
Por los tipos de datos podrás hacer unas gráficas circulares que ayuden a Perla a analizar la información de mejor manera para tomar decisiones.
Podrías hacer la gráfica circular de las ventas de comida corrida ya que le interesa más a Perla este tipo de ventas.
Realiza primero la tabla de frecuencia ordenada esta vez por día.
La tabla sería idéntica a la tabla de registro de perla sólo agregarás la última columna con la que obtendrás el ángulo del sector.
En la primera columna colocas los días de la semana y en la segunda, las frecuencias absolutas, 30, 62, 43, 67, 90 y 98, correspondientes a casa día
Ahora para poder encontrar el ángulo del sector, hay que obtener el total y establecer la proporción.
La adición de las frecuencias absolutas obtienes 390, y para la proporción puedes obtenerla dividiendo 360° entre 390, al simplificar se tiene que a cada comida corrida vendida le corresponde un ángulo de 12 treceavos de grado.
El ángulo se obtendrá multiplicando los 12 treceavos por la frecuencia absoluta de cada día, en el primer caso es de 30, lo escribes en forma de fracción y quedaría 12 treceavos por 30 sobre uno, multiplico directo,12 por 30 que es 360 y 13 por 1 que da 13, obtengo la fracción 360 treceavos, como número mixto sería 27 enteros 9 treceavos en grados. Para el martes al resolver las operaciones correspondientes, obtienes un ángulo de 57 enteros con 3 treceavos de grado.
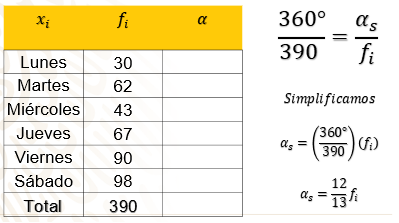
Para el miércoles se vendieron 43 comidas, lo que representa un ángulo de 39 grados y 9 treceavos; el jueves el valor es de 67, al multiplicarlo por los 12 treceavos se obtiene
61 grados y 11 treceavos.
El viernes la frecuencia es de 90, y le corresponde un ángulo de 83 grados 1 treceavo.
Por último, el sábado hay 98 comidas, que les corresponde un ángulo de 90 grados y 6
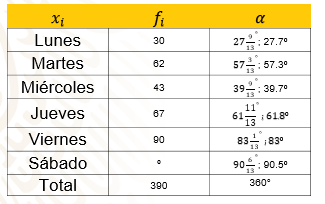
Ahora observa la tabla completa, como las medidas representan números mixtos, y para poder medir los ángulos con el transportador, puedes redondear las medidas a una cifra decimal. La medida no será exacta, pero habrá una mínima variación, que no será notoria.
Para el lunes son 27° y 9 treceavos, lo escribes como 27.7º; el martes son 57° con 3 treceavos, 57.2º; en el miércoles hay 39° y 9 treceavos, 39.7º. El jueves son 61 grados con 11 treceavos; 61.8º; el viernes el ángulo es de 83° y 1 treceavo; 83º y para el sábado, 90° con 6 treceavos 90.5º, que suman 360º.
Con estos datos ya tienes lo suficiente como para poder hallar los ángulos de cada sector.
Sigue los procedimientos vistos antes, traza ángulos adyacentes al anterior hasta completar la gráfica.
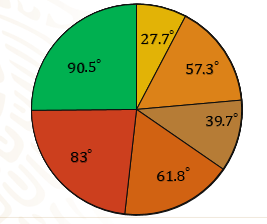
Observa la gráfica cómo quedó con todo y sus rótulos, con la información puedes observar que los lunes y miércoles la venta de comida corrida es menor, también es visible que el viernes y sábado las ventas son las más altas.
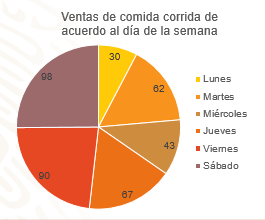
Sería recomendable para Perla que cambie el platillo que hace los lunes y miércoles para su comida corrida, tu ¿qué le recomendarías?
Perla podría hacer más encuestas para conocer que platillo les gustaría probar a los comensales que visitan el lunes y miércoles o incluso repetir el platillo del viernes o sábado alguno de esos días.
La gráfica circular ofrece una forma práctica, de acceder a la información de alguna situación, pero su interpretación y utilidad radica en que el observador tenga la posibilidad de interpretarla.
Siempre y cuando la gráfica cuente con todos los rótulos necesarios, ya que, si no los tiene, la gráfica no podría ser interpretada correctamente.
El reto de hoy:
Estos fueron solo unos ejemplos de la construcción, y uso de la gráfica circular, nota que para su construcción te apoyas en la tabla de frecuencia, la cual aún tiene muchos datos que ofrecer y su manejo es importante en el campo de la estadística, revisa tu libro de texto, seguro encontraras más situaciones interesantes y seguramente profundizarás en el estudio de la gráfica circular.
Realiza las actividades que contiene tu libro de texto.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/