Conociendo las ecuaciones cuadráticas
Conociendo las ecuaciones cuadráticas
Aprendizaje esperado: resuelve problemas que implican el uso de ecuaciones de segundo grado.
Énfasis: justificar operaciones inversiones.
¿Qué vamos a aprender?
Estudiarás las ecuaciones de segundo grado o cuadráticas de la forma más sencilla, la Ax2 + B = 0, explorarás con soluciones personales, y conocerás las operaciones inversas necesarias, formalizarás su solución y resolverás problemas.
También conocerás los elementos que las componen y resolverás problemas con métodos propios. En esta sesión necesitarás tu cuaderno, un lápiz y una regla.
¿Qué hacemos?
¿Te gustan los cuentos? Lee con atención la narración del siguiente cuento.


Una ecuación, es una igualdad entre dos expresiones (miembros de la igualdad) que contienen una o más literales llamadas incógnitas, es decir, una cantidad desconocida.
Observa las siguientes situaciones.
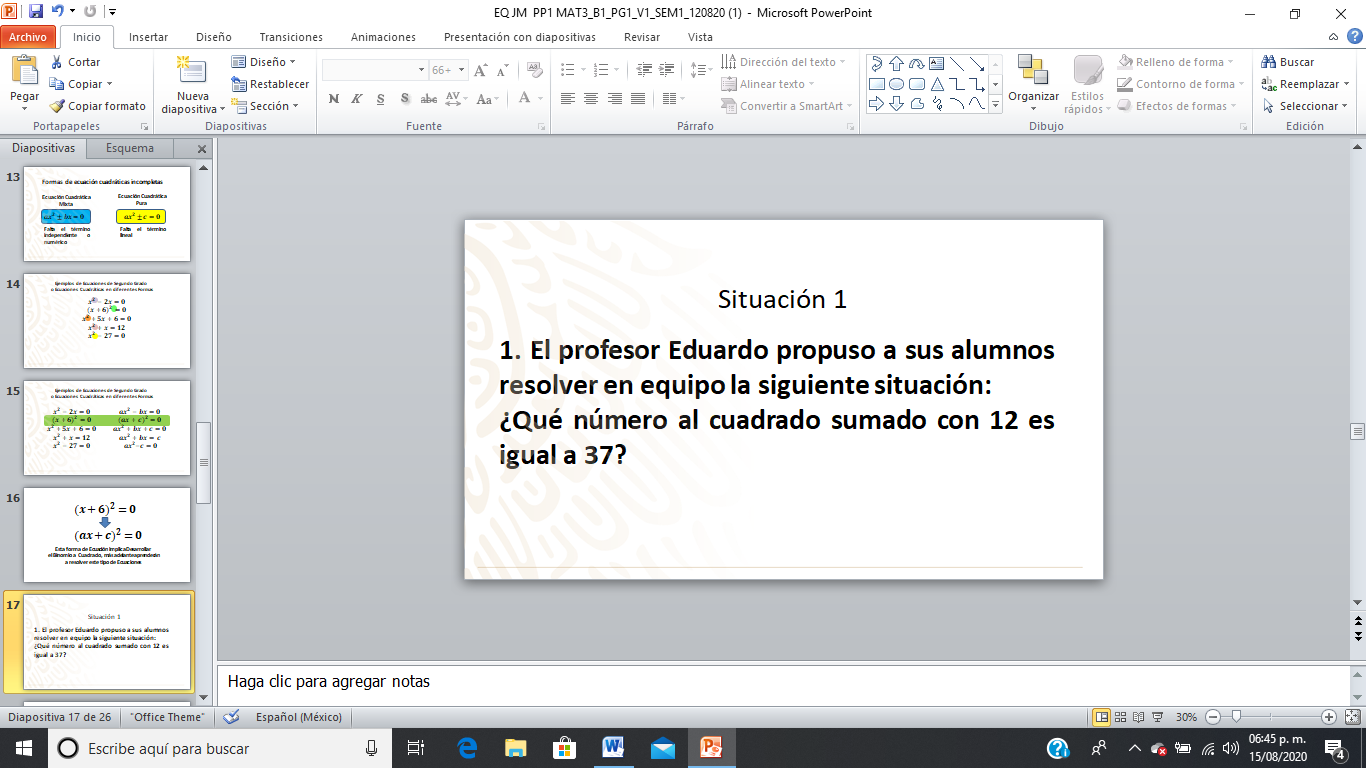
¿Cómo resolverías la anterior situación utilizando algún procedimiento ya aprendido? ¿Qué es lo primero que harías?
Una alumna del equipo 1 propuso que primero hay que plantear la ecuación necesaria para resolver el problema, ella pasó al pizarrón y escribió la siguiente ecuación:
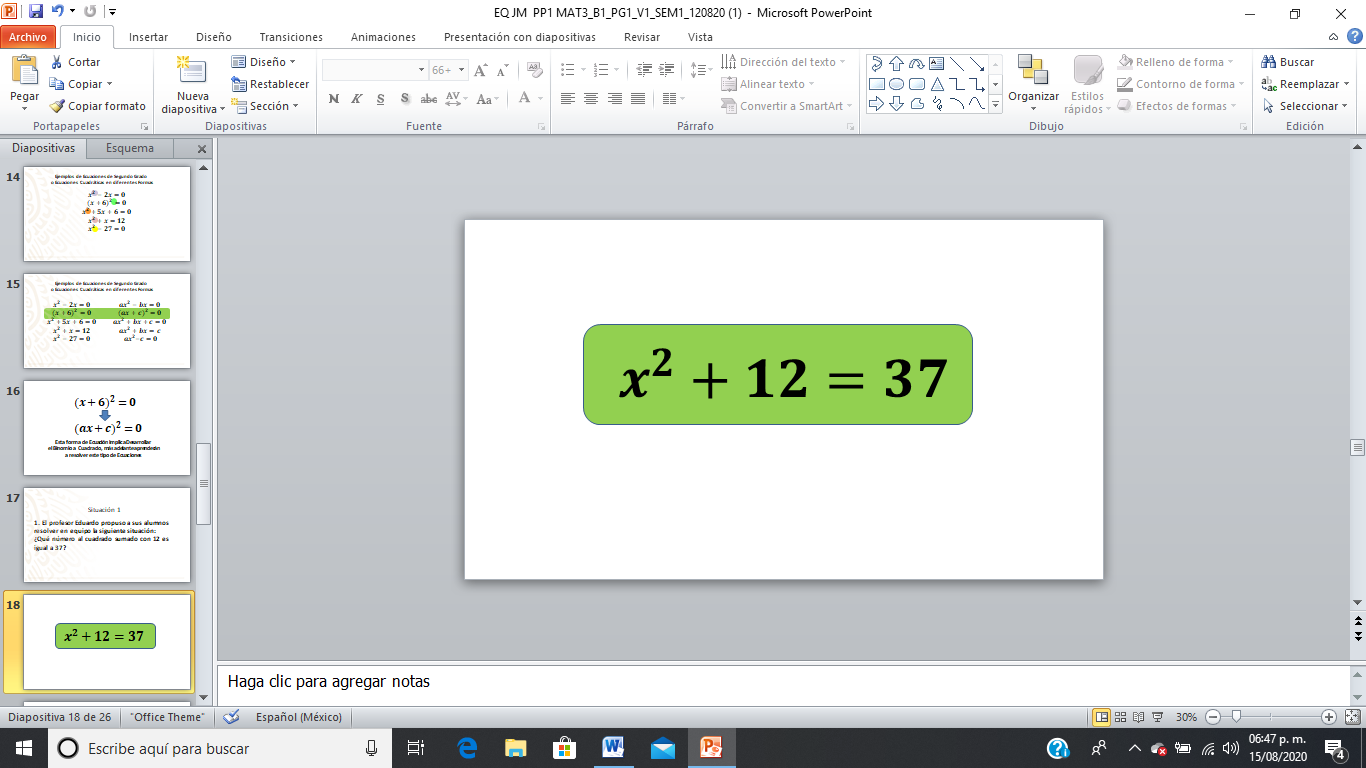
Una vez planteada la ecuación los alumnos de cada equipo comenzaron a analizar cómo resolver la ecuación propuesta. Después de un tiempo, uno de los alumnos integrante del equipo 5 expuso ante sus compañeros cómo resolvieron la ecuación planteada.
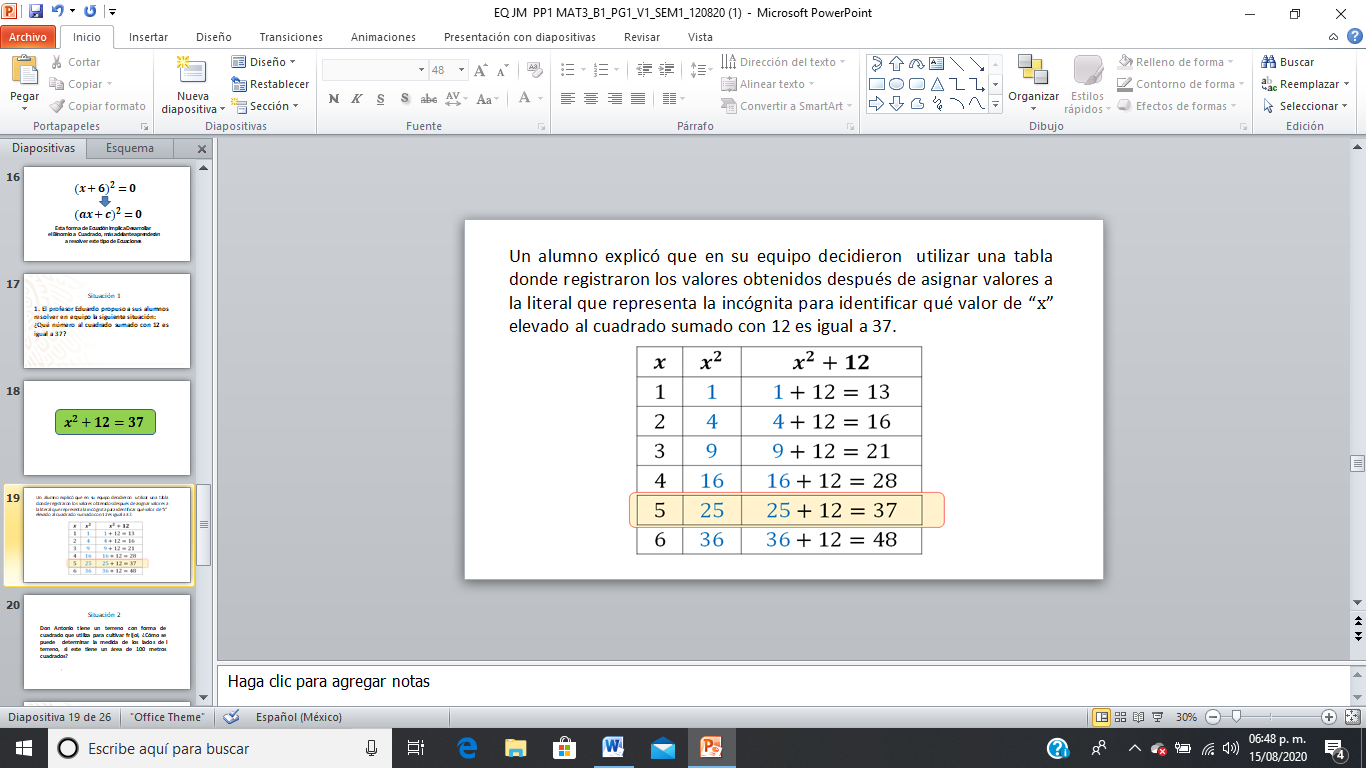
Como puedes observar en la tabla cada valor asignado a la incógnita equis es elevado al cuadrado y luego se suma 12, este procedimiento lo efectuaron hasta encontrar el valor de la incógnita que hace verdadera la igualdad. Los alumnos del maestro Eduardo encontraron que la incógnita es igual con 5.
Ahora, lee y analiza la siguiente situación:
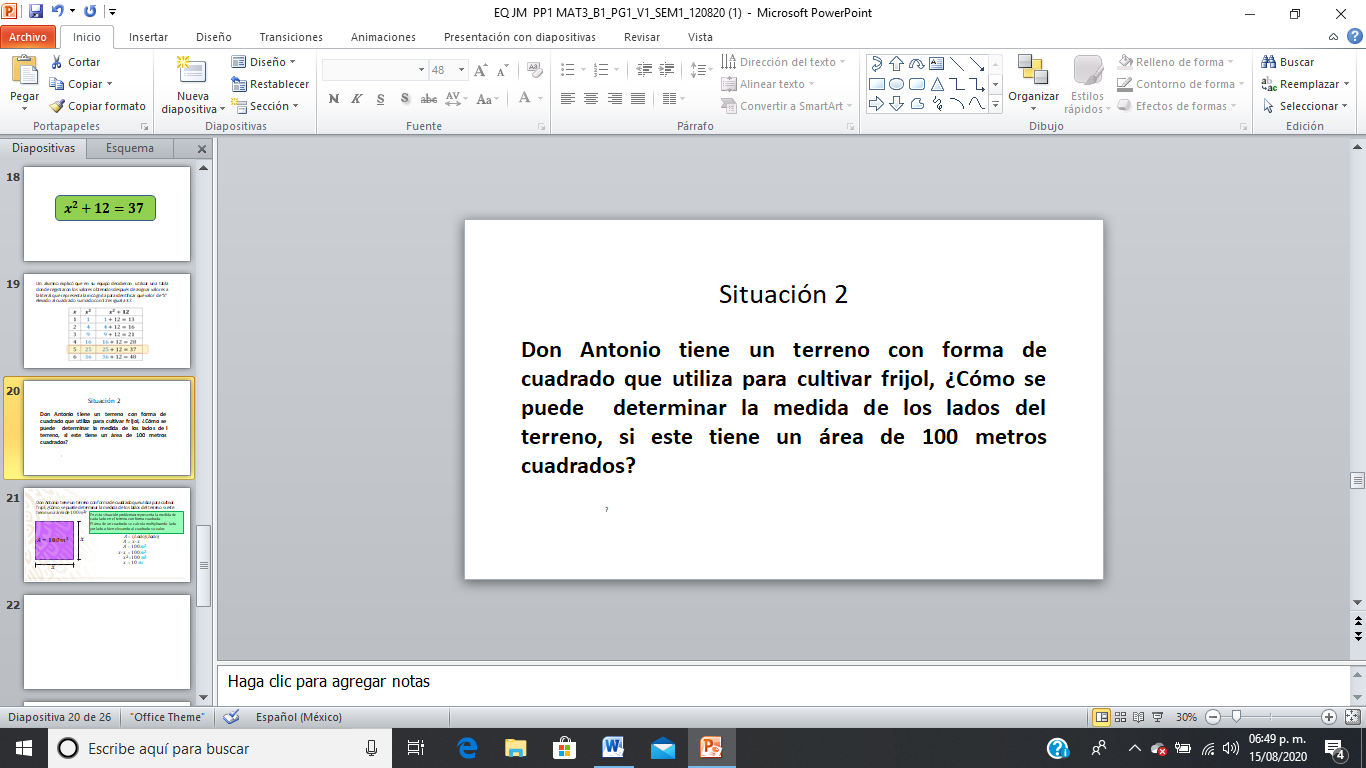
Observa el análisis y la resolución de la situación propuesta.
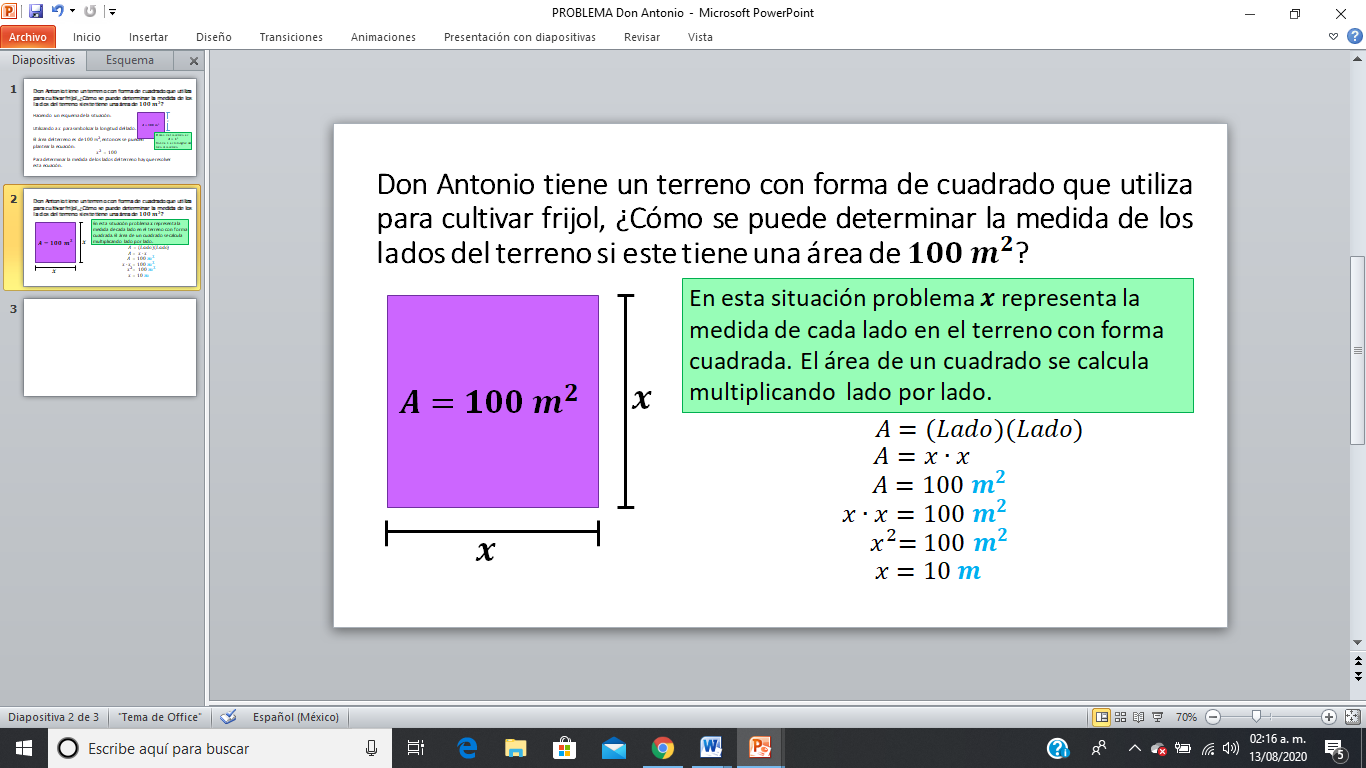
Para resolver situaciones como esta en matemáticas es muy útil modelar o representar de manera gráfica los datos, en este caso puedes dibujar un cuadrado, sabes que la medida de su área es 100 metros cuadrados, pero desconoces la medida de cada lado, entonces le puedes llamar equis porque es un dato desconocido.
Recuerda que el área de un cuadrado se calcula multiplicando lado por lado, aunque también en ocasiones sea base por altura, largo por ancho.
Aquí la reflexión se centra en que tengas en cuenta que el número que multiplicado por sí mismo y cuyo producto es 100 metros cuadrados es 10 metros el cual corresponde a la medida de cada lado del cuadrado.
Observa la siguiente situación es muy sencilla.
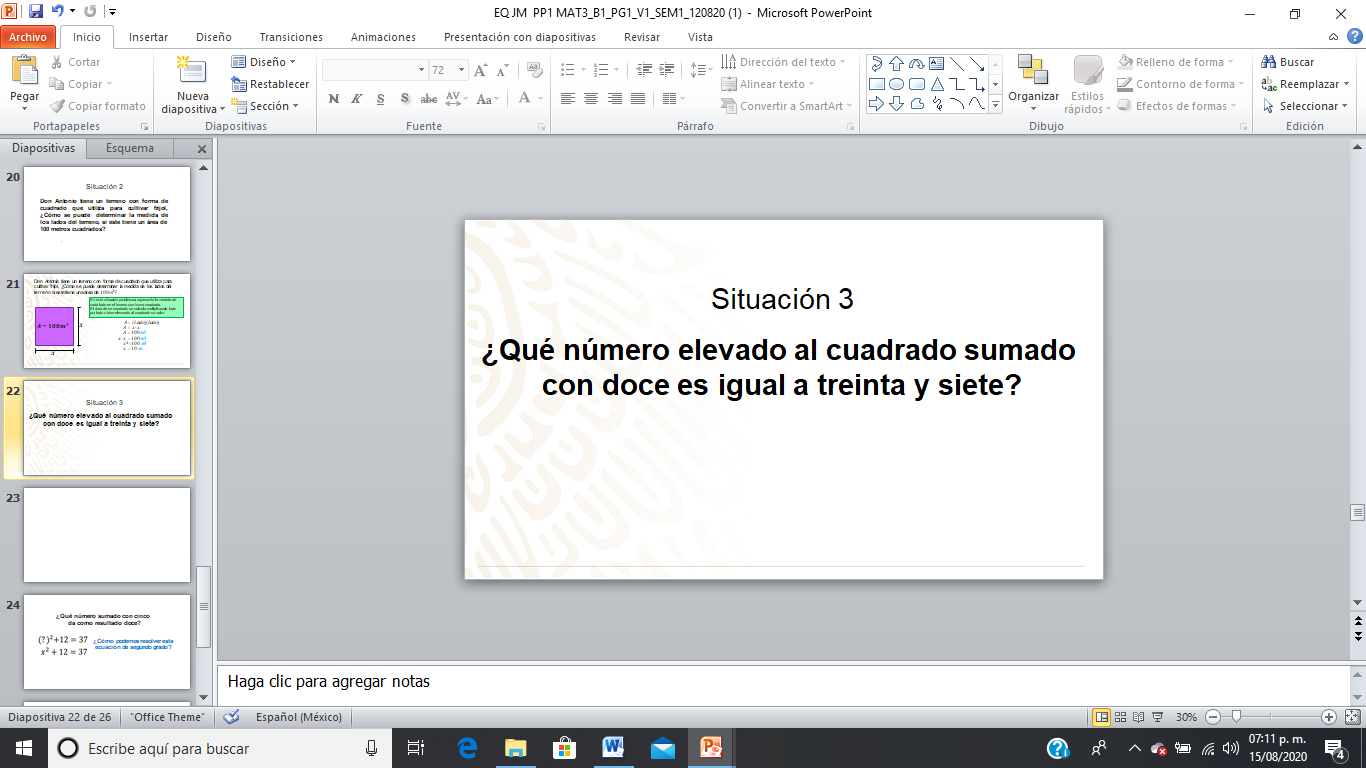
Como puedes observar la situación planteada requiere de determinar ¿Qué número elevado al cuadrado sumado con doce es igual a treinta y siete? Piensa ¿Cuál es la ecuación que modela esta situación?
La ecuación es:
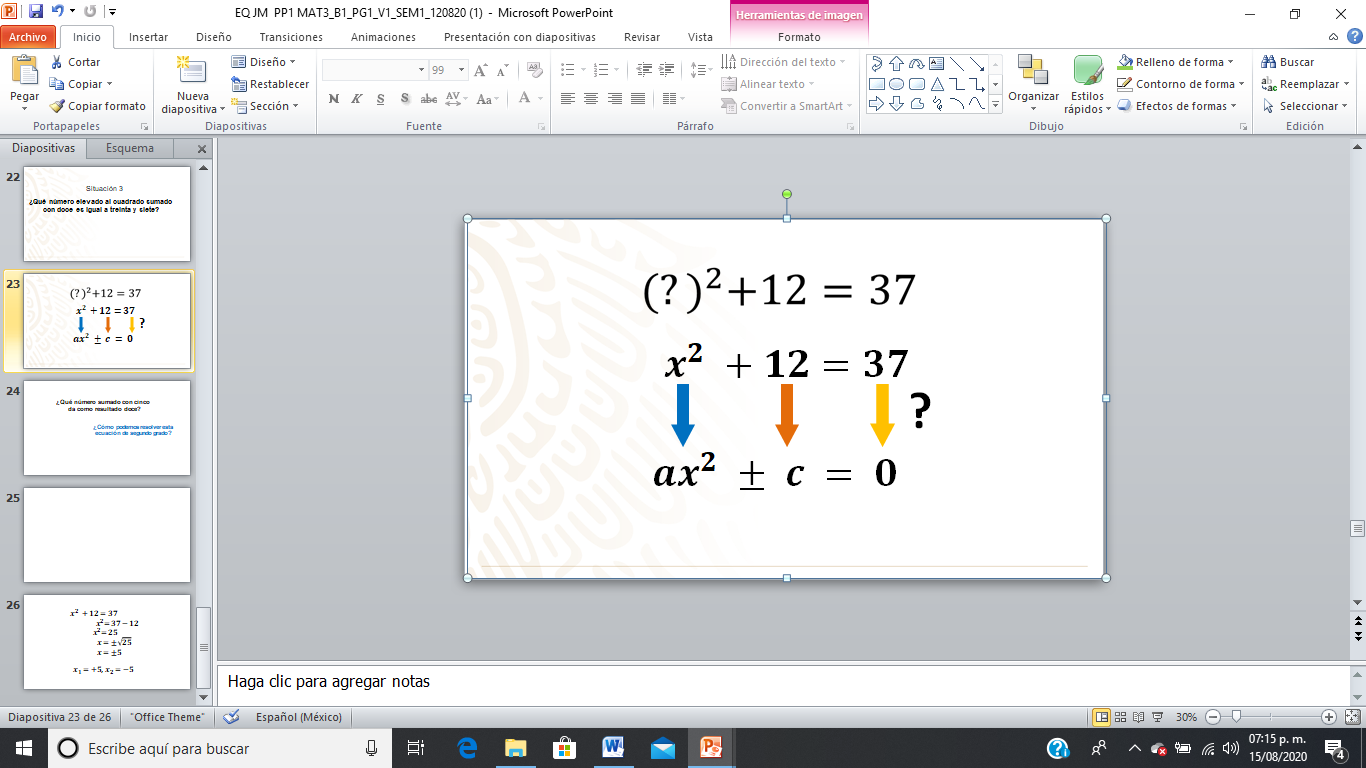
¿Qué observas de diferente en esta ecuación comparada con la forma ? La expresión del primer miembro no está igualada con cero, ¿Qué harías para que sea similar a la forma: ?
Necesitas transponer o cambiar el 37 que está en el segundo miembro al primer miembro, luego, una vez que la ecuación queda expresada similar a la forma:
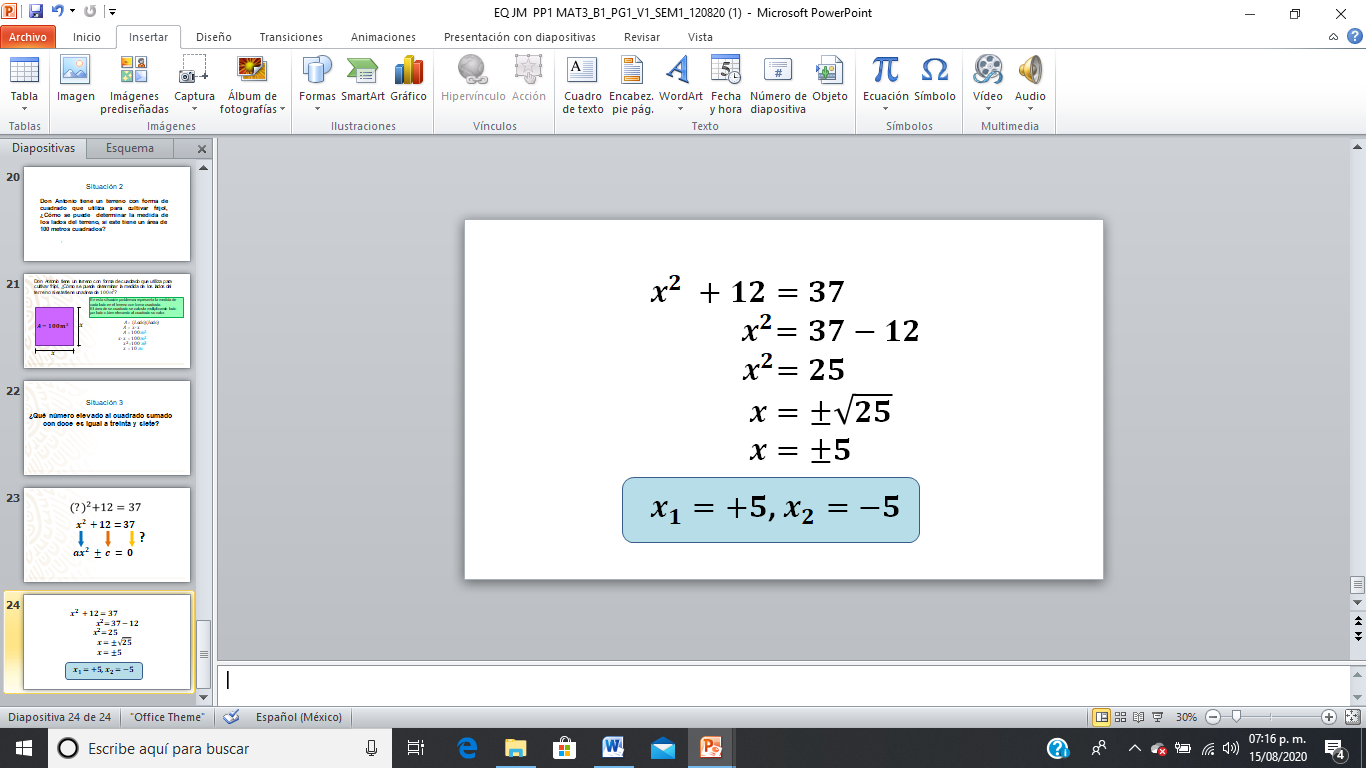
Procede a resolverla despejando la incógnita.
Recuerda que despejar la incógnita requiere que cambies de lugar o de miembro al 25 que está restando al otro miembro, después hay que pasar el exponente dos de la equis indicando la raíz cuadrada del 25 que está en el segundo miembro. ¿Qué valor obtuviste?
Ahora bien, otra forma es la siguiente:

Resuelve los siguientes ejercicios de ecuaciones de segundo grado considerando identificar la forma de cada una para determinar el procedimiento de resolución:
Conocerás el juego del Ajedrez,

Esta dinámica, se desarrolla sobre un tablero, se lleva a cabo entre dos personas, donde cada jugador cuenta con dieciséis piezas que pueden desplazar con ciertas reglas sobre el tablero. El juego se define cuando un jugador consigue que el rey del rival no pueda evitar un movimiento de captura, dicha jugada se le conoce como jaque mate.
Resuelve el siguiente problema:
Se quiere construir un tablero para jugar ajedrez, si quieres que cada casilla tenga 3 cm por lado, ¿De cuánto tendría que ser el tablero? Recuerda que un tablero de ajedrez tiene 8 casillas por lado.
- Reflexiona sobre cómo podrías resolver este problema.
Para comenzar puedes dibujarlo en tu cuaderno, y hacer las anotaciones que necesites. ¿Qué datos debes conocer? ¿Los tienes? ¿Lograste resolverlo?
Considera lo que significa elevar al cuadrado: es multiplicar un número por sí mismo, es decir, si tienes un solo elemento, significa multiplicar 1×1, pero si estas unidades son geométricas, se forma un cuadrado, si se eleva al cuadrado dos, tres, cuatro, tienes cuadrados con base y altura 2, 3 y 4.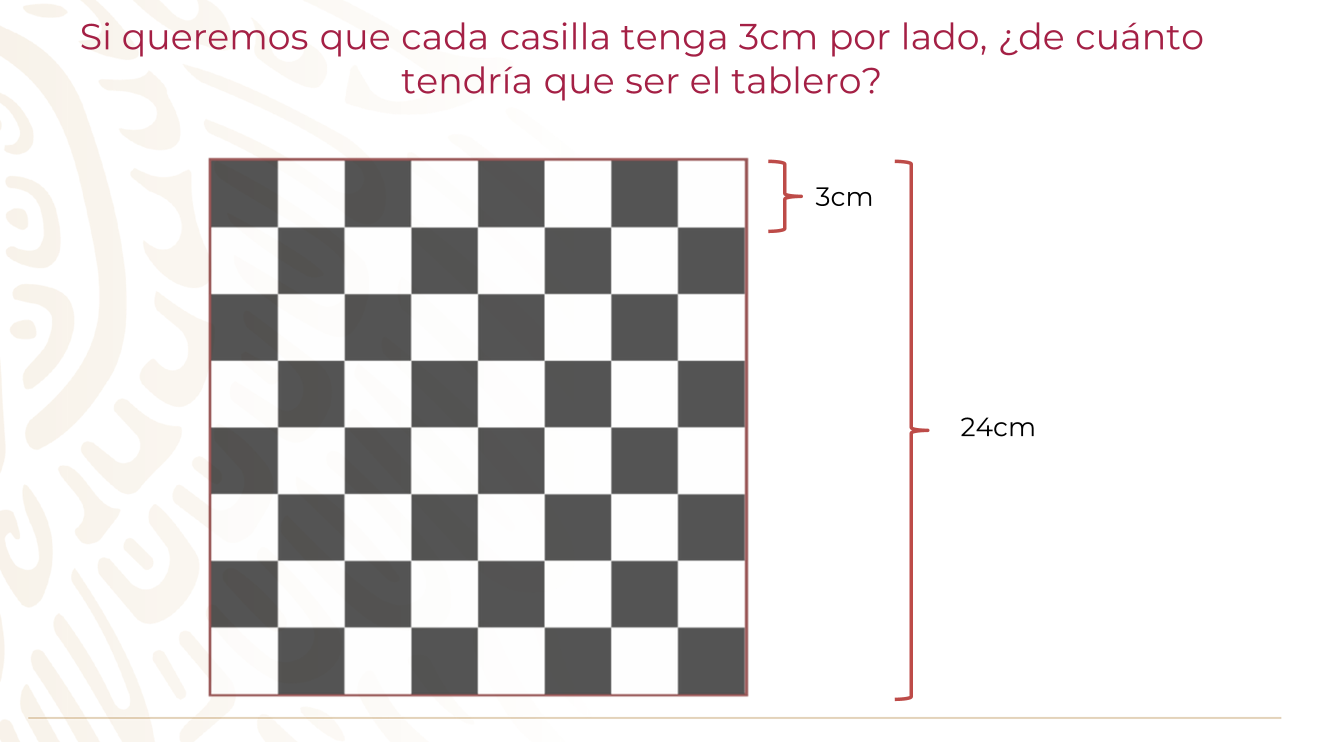
- Resuelve:
Sabes dos cosas, que cada casilla mide 3 cm por lado, y que el tablero de ajedrez tiene 8 casillas por cada lado entonces:
Un lado del tablero mide: 24 cm
Recuerda que para obtener este valor solo debiste haber multiplicado los 3 cm que mide de cada lado de la casilla por las 8 casillas. Ahora tienes que determinar cuánto mide el área del tablero.
Si ya tienes un lado y es un cuadrado, recuerda que, para obtener el área de ese cuadrado, solo debes multiplicar lado por lado, es decir 24 cm por 24 cm.
Y obtienes que el tablero que necesitas construir tendría que ser de 576 cm2. - Ahora bien vas a calcular, cuál sería el área de una de las casillas que forma el tablero.
Para calcular el área de cada casilla, sabes que mide 3 cm por lado, por lo que su área es de 9 cm2. ¿Qué estrategia utilizaste para llegar al resultado?
Conocerás otra manera de resolver este ejercicio.
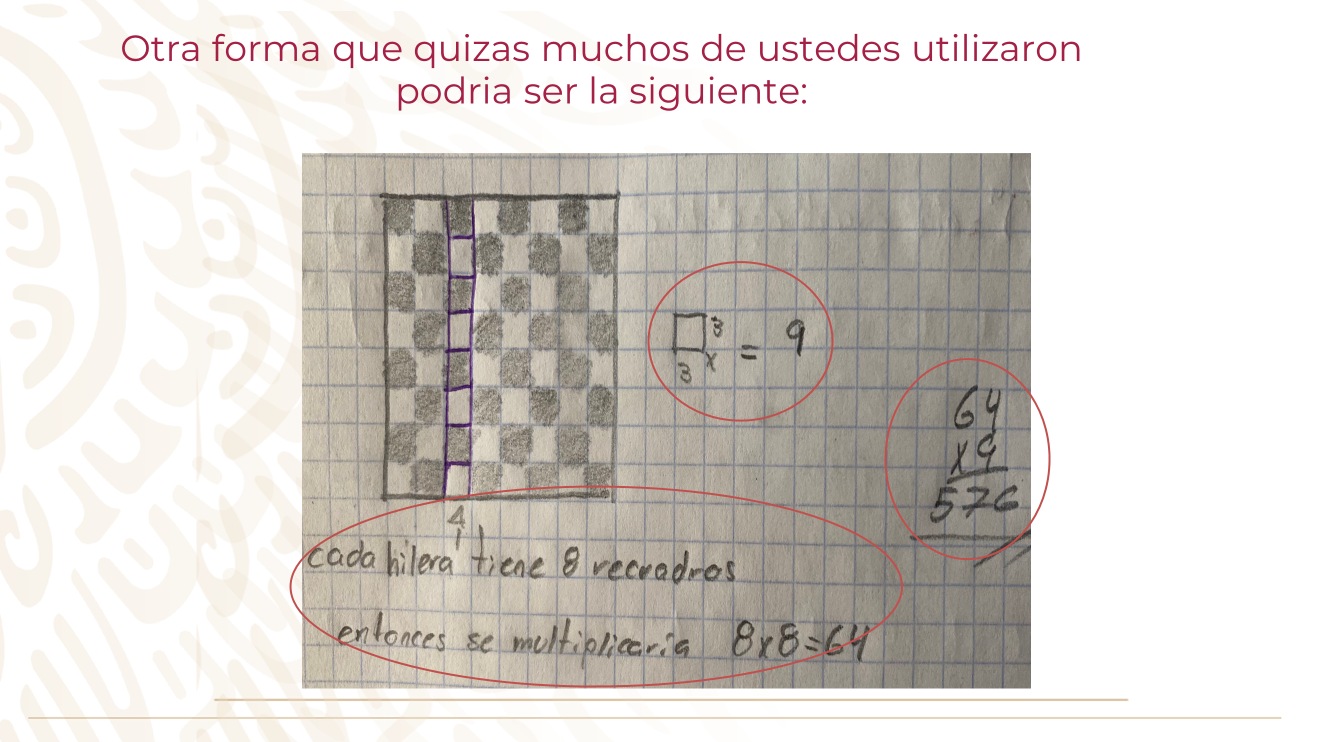
Calculaste primero, el área de una casilla, si sabes que un lado del cuadrado mide 3 cm, entonces, se obtiene multiplicando 3 cm x 3 cm y obtienes que el área mide 9 cm2.
Por otro parte sabes cada lado del tablero tiene 8 casillas y como es un cuadrado en total tendrías 64 casillas en el tablero. Por lo tanto, si multiplicas las 64 casillas por el área de cada casilla que es de 9 cm2 obtienes que el área del tablero sería de 576 cm2.
Ahora bien, ¿Cómo le harías para construir tu propio tablero de ajedrez?
¿De cuánto tendrían que ser las medidas de sus lados si quisiera que el tablero midiera 64 cm2?
¿De cuánto tendrían que ser las medidas de sus lados si quisiera que el tablero midiera 121 cm2?
Resuelve las preguntas anteriores:

¿De cuánto tendrían que ser las medidas de sus lados si quisiera que el tablero midiera 64 cm2?

¿De cuánto tendrían que ser las medidas de sus lados si quisiera que el tablero midiera 121 cm2?
Ahora bien, tomando en cuenta todos estos elementos:
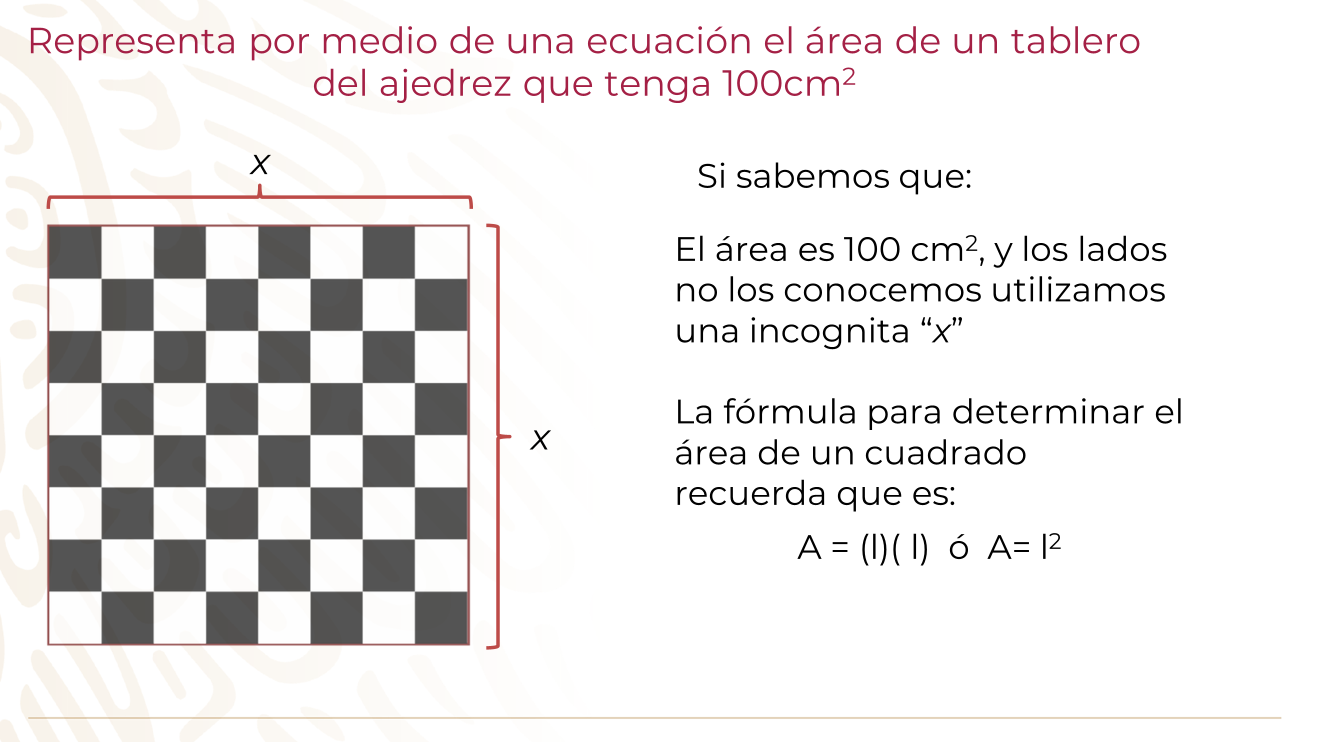
¿Cómo podrías representar por medio de una ecuación el área de un tablero de ajedrez que tenga 100cm2?
Inténtalo tienes todos los datos para poder formarla.
- Observa si llegaste al mismo resultado:
- El área es 100 cm2, y los lados no los conoces, por lo que utilizas una incógnita “x”.
- Como sabes que estás trabajando con áreas de cuadrados, utilizas la fórmula para determinar el área de un cuadrado recuerda que es: A = (l)(l) ó A= l2

- ¿Qué números multiplicados por sí mismo, dan como resultado 100cm2?
Haz ahora un truco de magia, utilizando las matemáticas:
Sigue las indicaciones y realiza las operaciones que se te vayan indicando.



Hazlo ahora con el número que desees:
- Piensa en un número (el que tu prefieras).
- Enseguida multiplícalo por 4.
- Réstale el número 3.
- A tu resultado multiplícalo por 2.
- Súmale el número 6.
- Y por último divídelo entre el número que pensaste.
¿Volviste a obtener 8?
Magia, ¿verdad?
Recuerda que una ecuación, es una igualdad entre dos expresiones que contienen una o más literales llamadas incógnitas, es decir, una cantidad desconocida que se puede calcular.
Seguramente recurriste a tu habilidad de cálculo mental, para identificar qué número multiplicando por sí mismo da como resultado cien en la situación problema propuesta.
Es importante que tomes en cuenta que resolver una ecuación de segundo grado implica calcular qué valores tiene la incógnita y que estos hagan verdadera la igualdad.
Busca en tu libro de texto problemas y ejercicios similares a los que estudiaste y los resuelvas. Recuerda que compartir es la mejor forma de reforzar lo que has visto.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: