Congruencia de triángulos en cuadriláteros
Congruencia de triángulos en cuadriláteros
Aprendizaje esperado: resuelve problemas de congruencia y semejanza que implican, utilizar estas propiedades en triángulos o en cualquier figura.
Énfasis: resolver problemas que impliquen las propiedades de congruencia de cuadriláteros.
¿Qué vamos a aprender?
Te sugerimos tener a la mano tus anotaciones de la clase anterior.
¿Recuerdas que es un cuadrilátero?
¿Qué hacemos?
Los cuadriláteros son polígonos con 4 lados, 4 ángulos y 4 vértices. A los cuadriláteros solo es posible trazarles 2 diagonales, recuerda que las diagonales son los segmentos que unen dos vértices no consecutivos.
La suma de los ángulos interiores de un cuadrilátero es 360°, una manera de mostrar que esto es cierto es trazando a cualquier cuadrilátero una diagonal, observa: ¿Cuántos triángulos se forman? dos y si la suma de los ángulos interiores de un triángulo es 180°, entonces de 2 triángulos son 360°.
Los cuadriláteros se clasifican en paralelogramos, trapecios y trapezoides, observa las características que tienen cada uno de ellos.
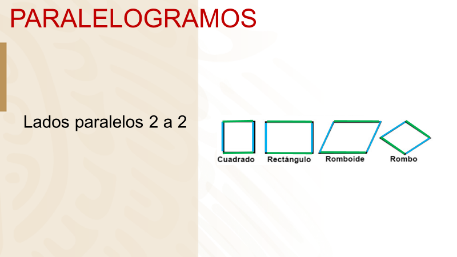
Paralelogramos: Cuadriláteros con 2 parejas de lados paralelos iguales.
Observa las parejas de lados paralelos iguales.
Los paralelogramos son el cuadrado, rectángulo, romboide y rombo.
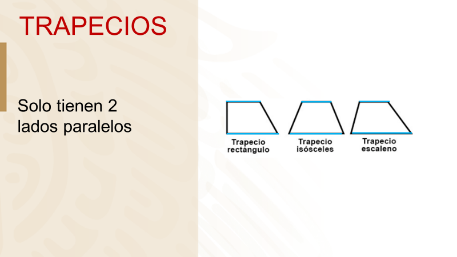
Trapecios: Cuadriláteros que solo tienen 2 lados paralelos. ¿Puedes notar sus 2 lados paralelos?
Los trapecios son 3: Trapecio rectángulo (tienen un ángulo interior de 90°), Isósceles (dos de sus lados son iguales) Escaleno (todos sus lados son diferentes.
Y los trapezoides: Son cuadriláteros sin lados paralelos.
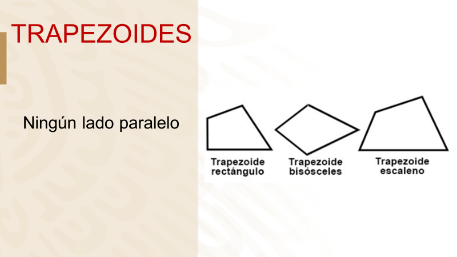
Ya aprendiste la clasificación de cuadriláteros ahora analizarás sus diagonales, recuerda que el segmento que une dos vértices no consecutivos de un polígono recibe el nombre de diagonal.
Observa el siguiente video para consolidar lo anterior.
- Propiedades de los paralelogramos.
https://www.youtube.com/watch?v=cFAalCAY3XE
Contesta las siguientes preguntas:
- ¿Cuántas diagonales puedes trazar en cualquier cuadrilátero?
- ¿En qué cuadriláteros las diagonales son perpendiculares, es decir forman ángulos de 90°?
Si trazas las 2 diagonales de los paralelogramos, trapecios y trapezoides, ¿En qué cuadriláteros las diagonales son perpendiculares, es decir forman ángulos de 90°?
Responde, ¿En qué cuadriláteros las diagonales son perpendiculares? En el cuadrado y el rombo, las diagonales forman ángulos de 90° en consecuencia son perpendiculares.
- ¿En qué cuadriláteros las diagonales son iguales?
Los paralelogramos al trazar sus diagonales estas son iguales.
Te sugerimos resolver el siguiente problema.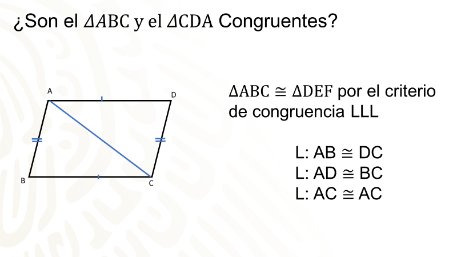
Recuerda que en sesiones anteriores has estudiado uno de los criterios de congruencia de triángulos.
Observa que el polígono ABCD es un romboide, el romboide se encuentra dentro de los paralelogramos por lo tanto tiene 2 pares de lados paralelos e iguales.
AD BC y AB DC
AC es una diagonal del romboide.
Por las propiedades del romboide se puede determinar que AB DC y AD BC
Observa que AC es el mismo lado para el y el
Por lo tanto, por el criterio LLL porque:
AB DC
AD BC
AC AC
¿Te diste cuenta de que sin conocer sus medidas pudiste determinar que ambos triángulos son congruentes? Para eso sirven los criterios de congruencia.
Para reforzar, resuelve otro problema con cuadriláteros.
Pedro les dio a sus hijos (Camila y Mauricio) un chocolate en forma de trapecio, le pidió a Mauricio que lo repartiera, y él decidió dividirlo como se muestra en la figura.
Le dio el trozo 1 a Camila y él se quedó con el trozo 2, pero Camila muy enojada le reclamó diciéndole que la repartición no había sido igualitaria, porque a ella le tocó menos chocolate.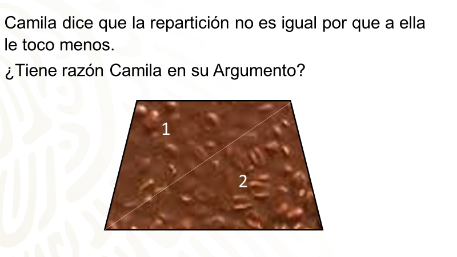
Observa con atención. - ¿Qué tipo de cuadrilátero es el chocolate?
- Por ser un trapecio, ¿Cuáles lados son iguales?
- ¿Son congruentes ambos trozos?
- ¿Tiene razón Camila?
Resuelve.
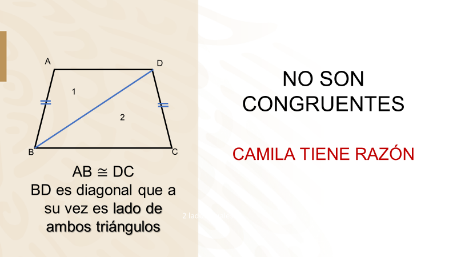
Sabes que el chocolate es un trapecio por lo tanto solo tienen 2 lados paralelos BC.
También sabes que AB DC por ser un trapecio isósceles.
Puedes ver que el segmento BD es una diagonal del trapecio.
Con la información que tienes se puede determinar qué, el o los triángulos 1 y 2 son congruentes.
¿Hay condiciones para determinar si son congruentes por el criterio LLL?
La respuesta es: No, porque solo conoces que AB DC y BD que es la diagonal del trapecio, a su vez es lado de ambos triángulos, es decir, ambos triángulos solo tienen 2 lados iguales, por lo tanto, ambos trozos de chocolate no son congruentes y Camila tiene razón.
Resuelve otro problema.
¿Es el triángulo AEB congruente con el triángulo CED?
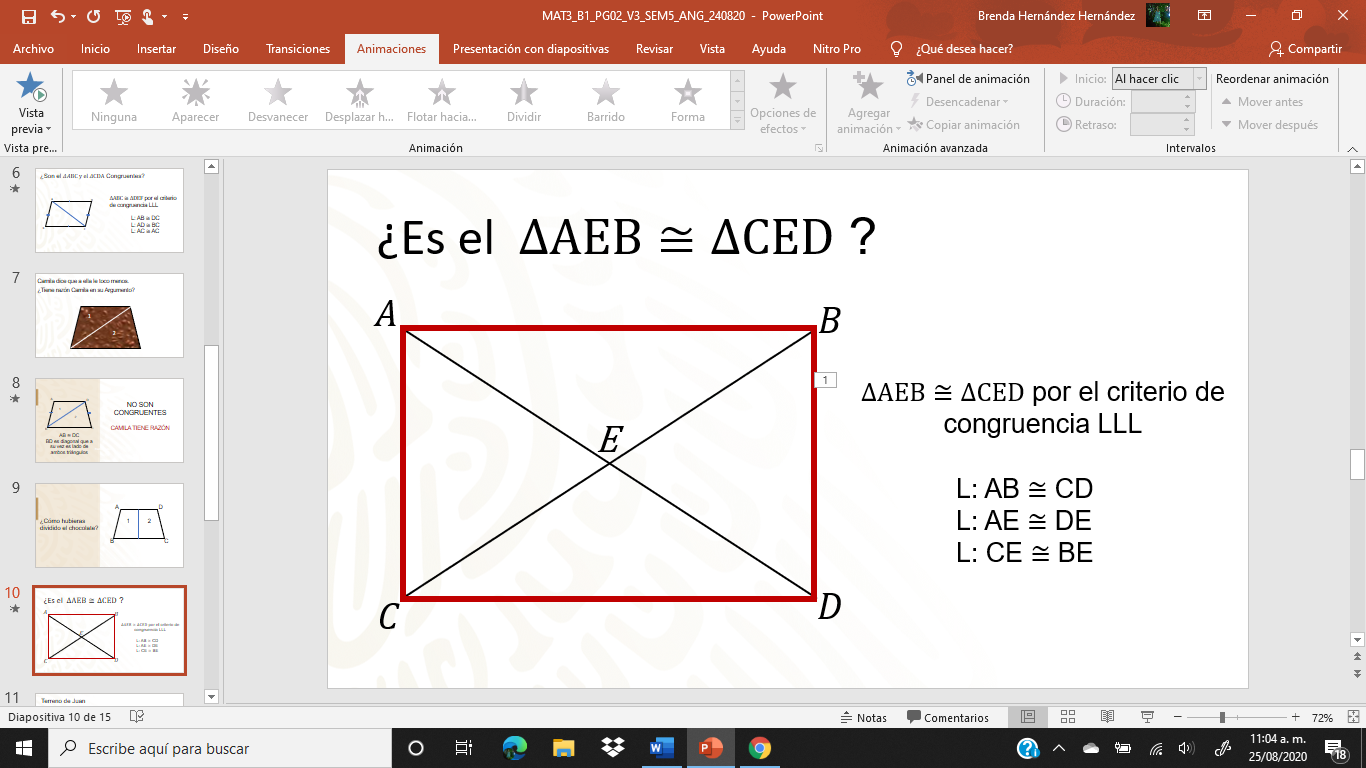
Para poder determinar si son congruentes, tienes que identificar algunas propiedades del rectángulo, observa, ABCDE es un rectángulo, éste pertenece a los paralelogramos, por lo tanto, tiene 2 pares de lados paralelos e iguales, entonces AB es igual a CD, también observa que AD es una diagonal del rectángulo y CB es también diagonal del rectángulo, ambas diagonales, son iguales y se cortan en su punto medio, es entonces que AE es igual a DE y CE es igual a BE, por lo tanto ambos triángulos tienen sus 3 lados iguales, esto quiere decir que:
por el criterio de congruencia LLL
L: AB CD
L: AE DE
L: CE BE
¿Te diste cuenta de que, sin conocer sus medidas, pudiste determinar que son congruentes haciendo uso de las características y propiedades de los cuadriláteros?
Observa otra situación apegada a la vida real:
Nahomi tiene un terreno que tiene la forma de un cuadrilátero, quiere construir su casa dentro del terreno de modo que ésta sea un cuadrilátero cuyas esquinas son los puntos medios de cada lado del terreno.
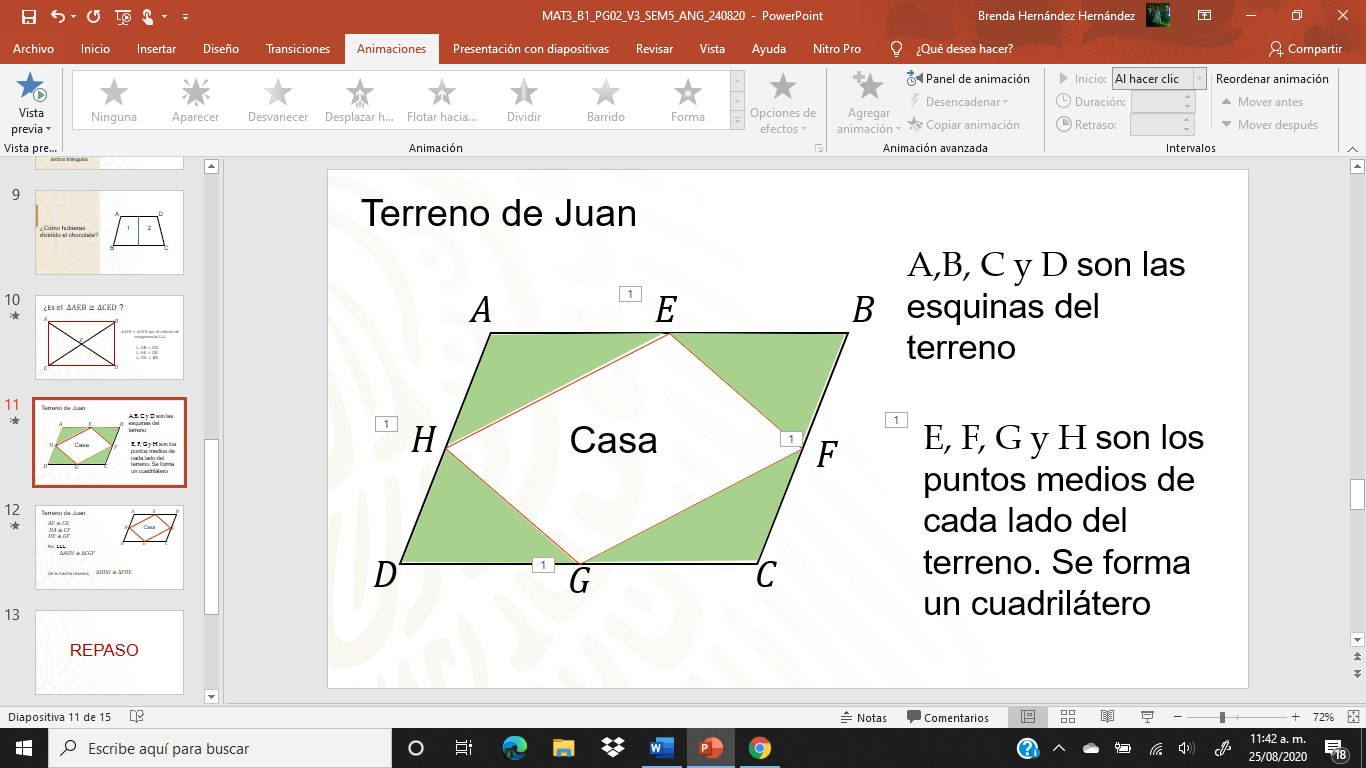
Observa que en el terreno ABCD, dentro hay un cuadrilátero EFGH, que será la casa, los puntos EFGH son los puntos medios de los lados del terreno. A Nahomi le interesa saber cómo quedan las demás partes del terreno, es decir, si el resto del terreno son triángulos iguales.
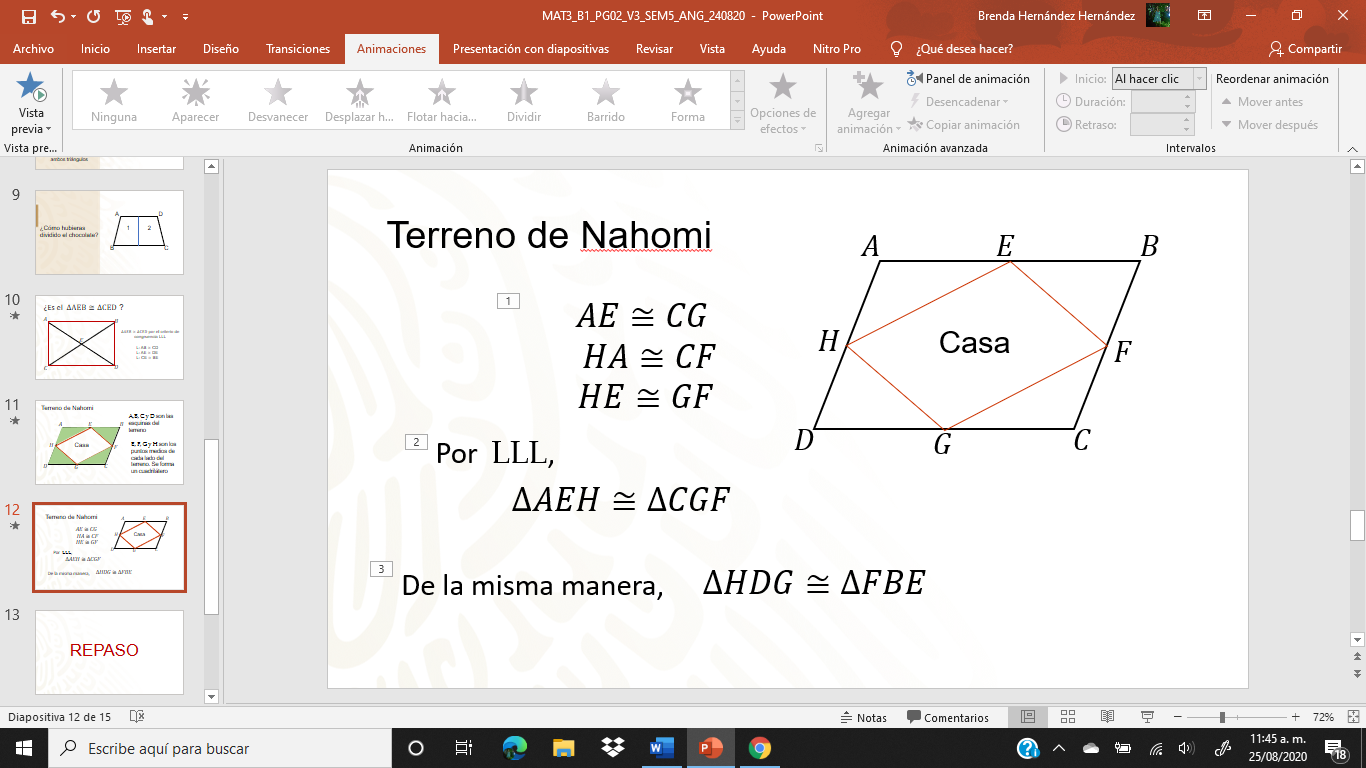
Debido a que ABCD y EFGH son cuadriláteros se tiene que:
Por lo tanto, ambos triángulos son congruentes por el criterio LLL
De igual manera entonces
Lo que se le puede decir a Nahomi, es que los terrenos que quedan después de diseñar la casa son dos parejas de triángulos congruentes opuestas entre sí. Se verá muy bonita la casa una vez construida, y si esos triángulos de terreno Nahomi pone pasto y arbolitos quedara aún más bonita.
Para reforzar los conocimientos adquiridos realiza un repaso:
Los cuadriláteros son polígonos con 4 lados, 4 vértices y 4 ángulos, y la suma de sus ángulos interiores es 360°
Los cuadriláteros se clasifican en:
- Paralelogramos: Cuadriláteros con 2 parejas de lados paralelos.
- Trapecios: Cuadriláteros que solo tienen 2 lados paralelos.
- Trapezoides: Cuadriláteros sin lados paralelos.
- Diagonal: Segmento que une dos vértices no consecutivos de un polígono.
En los cuadriláteros solo es posible trazar 2 diagonales.
Te sugerimos realizar un crucigrama. Recuerda que para armarlo debes descubrir las palabras que se entrecruzan, a partir de definiciones dadas.
Crucigrama: Palabras que se entrecruzan.
Tienes 5 fichas, en ellas se marca si el concepto que leerás corresponde a una fila o columna, es decir, horizontal o vertical, mientras lees el enunciado debes descubrir el concepto al que hace referencia.
1 VERTICAL
Cuadriláteros que solo tienen 2 lados paralelos.
Trata de recordar cuales son esos cuadriláteros.
Cuadriláteros que solo tienen 2 lados paralelos, “Trapecios”.
2 VERTICAL
Polígono con 4 lados, 4 ángulos y 4 vértices, y la suma de sus ángulos interiores es 360°
¿Qué nombre recibe ese polígono?
Excelente, “Cuadrilátero”.
3. HORIZONTAL
Segmento que une dos vértices no consecutivos de un polígono.
Diagonal es la respuesta.
4. HORIZONTAL
Cuadriláteros sin lados paralelos ¿Cuál es ese cuadrilátero?
Son los “Trapezoides”.
Ultima ficha para completar el juego.
5. HORIZONTAL
Cuadriláteros con 2 parejas de lados paralelos.
Muy bien, son los “Paralelogramos”.
¿Lograste resolver el crucigrama?
El reto de hoy:

Revisa en tu libro de texto de matemáticas la clasificación y propiedades de los cuadriláteros. Si es posible elabora un resumen o un mapa conceptual, en tu cuaderno de apuntes.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: