Congruencia de triángulos
Congruencia de triángulos
Aprendizaje esperado: resuelve problemas de congruencia y semejanza que implican utilizar estas propiedades en triángulos o en cualquier figura.
Énfasis: resolver problemas que impliquen las propiedades de congruencia de triángulos
¿Qué vamos a aprender?
Considerarás los conceptos de congruencia y semejanza en triángulos y cuadriláteros, observarás sus características y resolverás problemas. También, considerarás uno de los criterios que asegura la congruencia y otro que asegura la semejanza.
El propósito es definir la congruencia e identificar los criterios de congruencia de triángulos, en específico de un primer criterio de congruencia.

¿Qué hacemos?
Lee la siguiente reseña del autor Norton Juster, La recta y el punto, un romance matemático.

El libro trata de la historia de una línea recta que se enamora de un punto. Pero el punto encuentra a la línea aburrida y convencional, y se fija en un garabato. La línea se esfuerza y un día logra variar su forma. Es entonces que el punto se da cuenta de que el garabato -símbolo de la libertad y la diversión- es tan sólo caos y pereza. Así que lo abandona y elige a la recta, pronto la recta y el punto empiezan a hacer muchas figuras juntos, gracias a lo cual logran vivir, si no dichosos para siempre, al menos razonablemente felices.
La idea es que imagines la historia que lees y que potencies tu imaginación y creatividad.
La Recta y el Punto
“Había una vez una sensata línea recta, perdidamente enamorada de un punto:
- Tú eres el principio y el fin, el eje, el núcleo y la quinta esencia – le decía con ternura, pero el frívolo punto no estaba ni un poquito interesado, pues sólo tenía ojos para una línea curva, alegre y desparpajada, y con la cabeza hueca.
Iban juntos a todos lados.
Cantando y bailando y divirtiéndose y muriéndose de risa y quién sabe qué más… - Ella es tan alegre y libre, tan desinhibida y llena de vida
- Le dijo fríamente el punto a la recta.
-Y tú eres tiesa como un palo:
Aburrida, convencional y frustrada.
Rígida y estricta. Pasiva, tímida y amargada.
Oprimida, reprimida y reseca. - Mira, chiquita, regresa cuando te hayas enderezado un poco -agregó la curva con una risita rasposa, mientras perseguía al punto sobre el pasto.
¿Por qué me expongo a esto? -replico la recta
sin mucha convicción-. Merezco un trato mejor.
Yo sé lo que quiero…
¡Yo sí tengo dignidad!
Pero eso fue un triste consuelo para la desgraciada recta.
Cada día estaba más y más de malas.
Incluso dejó de comer y de dormir, y muy pronto, estaba completamente al margen.
Preocupadas, sus amigas
Se dieron cuenta de lo terriblemente flaca y pálida que la recta se había puesto, e hicieron lo posible por alegrarla. - Él no te merece.
- Le falta profundidad.
- Ya ves que todos son iguales.
¿Por qué no te busca un lindo trazo recto y sientas cabeza?
Pero la recta apenas prestaba atención a lo que le decían.
Lo viera por donde lo viera,
El punto le parecía perfecto.
Desde arriba
De perfil
De frente
Ella descubría en él cualidades que nadie podía imaginar.
-Es más guapo que cualquier otro trazo que haya visto- suspiraba la recta
Sus amigas movían la cabeza desesperanzadas.
Aunque respetaban sus sentimientos, se daban cuenta de que la cordura de la recta estaba rompiéndose por el punto más débil.
Y la recta se pasaba las horas soñando con el voluble punto e imaginándose a sí misma como la encarnación de todo lo que él admiraba.”
Si puedes lee el libro completo, lo puedes encontrar en la colección de los libros del rincón.
Para aprender a identificar los criterios de congruencia de triángulos, es necesario que actives tus conocimientos previos para que sea más sencillo de comprender el aprendizaje esperado.
Recuerda que la nomenclatura en matemáticas son símbolos para designar elementos, por ejemplo:
Los puntos o vértices de una figura se denotan con las letras mayúsculas del abecedario, como se observa en el rectángulo.
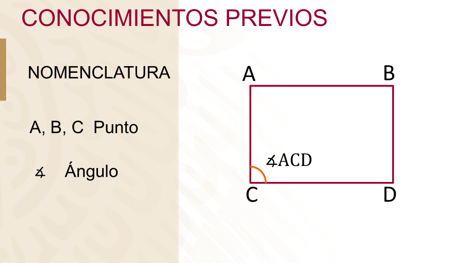
El símbolo para nombrar a un ángulo siempre se antecede a los vértices que forman al ángulo, por ejemplo, en la imagen se ha marcado el ACD
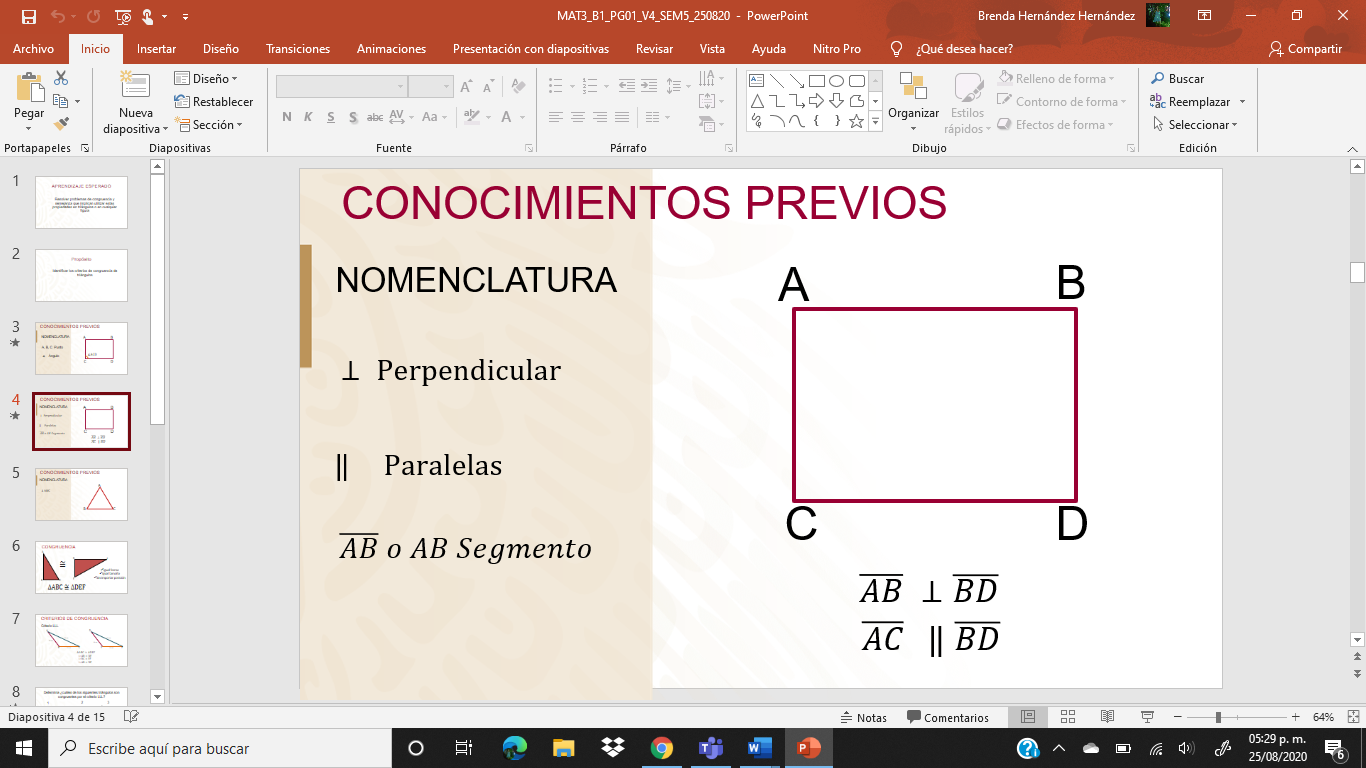
El símbolo de paralelas siempre se utiliza entre las rectas o segmentos de recta que son equidistantes, es decir, la distancia entre una y otra es la misma, de modo que al prolongarlas estas jamás se juntan, por ejemplo, ACBD.
Segmento, para representarlo se utilizan las letras de los dos puntos en que ésta comprendido, a veces se utiliza una barra arriba de las letras.
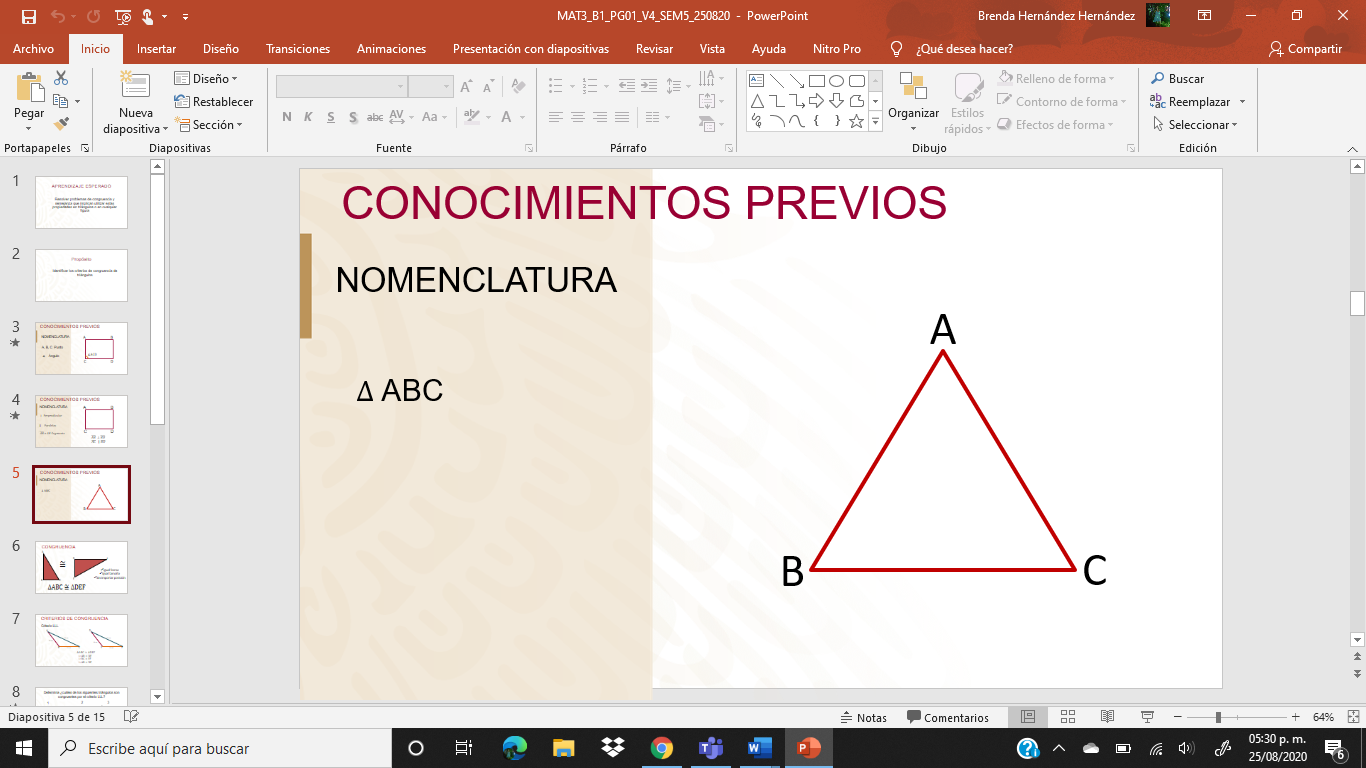
Triángulo, el símbolo se antecede a los 3 tres vértices que componen al triángulo, por ejemplo: ABC.
Además de la nomenclatura algo que debes recordar son los triángulos, éstos son figuras planas de 3 lados, 3 ángulos y 3 vértices. Recuerda, la suma de sus ángulos interiores es 180°
Observa el siguiente video:
- Suma de ángulos interiores de triángulos
https://youtu.be/JNpp2OmP13I D
Otra manera de mostrar la suma de los ángulos interiores de un triángulo es la siguiente: dibuja un triángulo y marca su altura (la altura es la línea perpendicular que une un vértice con su lado opuesto), ahora haz coincidir los tres ángulos del triángulo con ese punto. Observa cómo se forma un ángulo de 180°.
Recuerda los triángulos se clasifican según sus lados y según sus ángulos. Por sus lados encuentras al triángulo Equilátero (todos sus lados son iguales), Isósceles (tienen 2 lados iguales) y Escaleno (los 3 lados son distintos).
Según la medida de sus ángulos se clasifican en: Acutángulos (tienen los 3 ángulos agudos, es decir menor de 90°), Rectángulo (tienen un ángulo interior recto es decir de 90°) Y Obtusángulo (tiene un ángulo interior obtuso, es decir, mayor de 90°).
Una vez que has activado los conocimientos previos que te servirán a la comprensión del tema ahora estudiarás la congruencia en triángulos.
En matemáticas cuando dos figuras tienen la misma forma y mismo tamaño, se dice que son Congruentes, es decir:
- Dos segmentos de recta son congruentes si tienen la misma medida.
- Dos ángulos son congruentes si tienen la misma medida.
En consecuencia: dos triángulos son congruentes si las medidas de sus lados y ángulos son iguales.
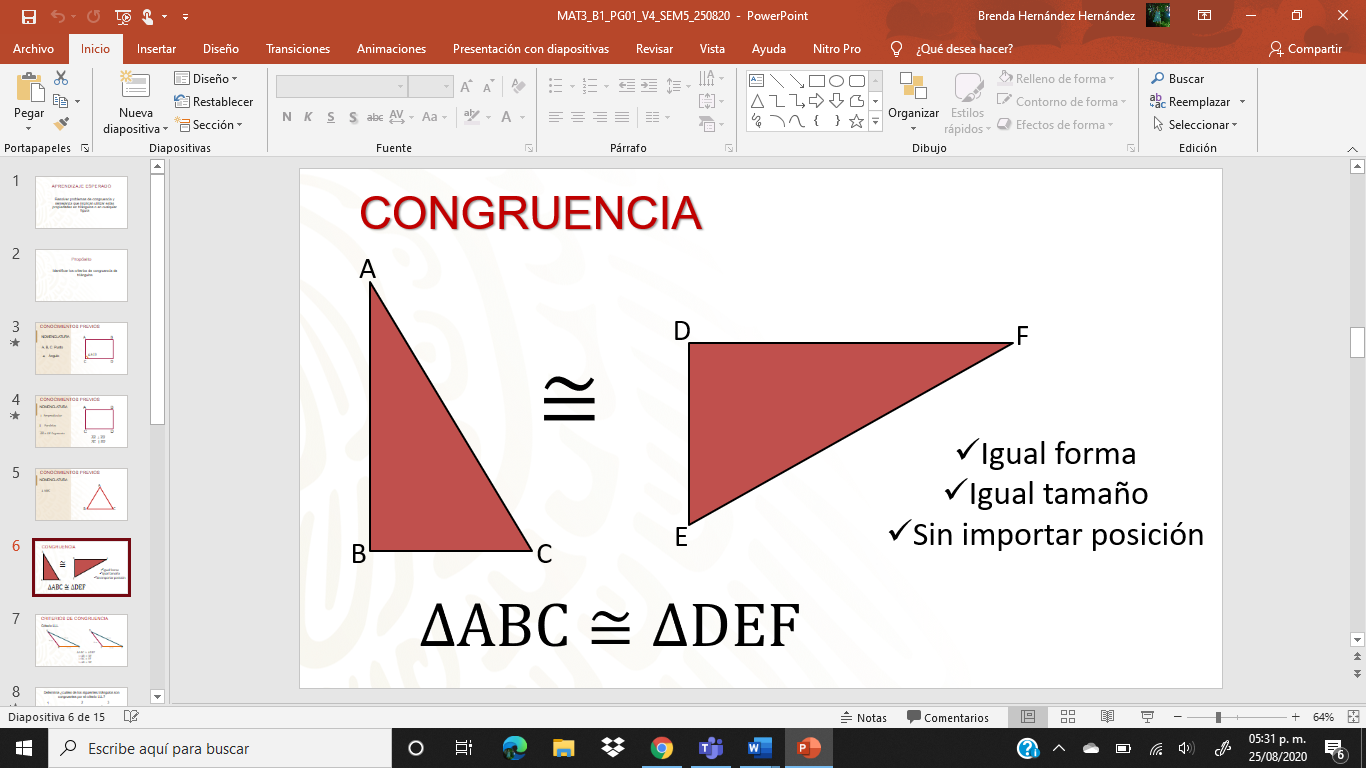
Este par de triángulos son congruentes y se utiliza un símbolo formado por un signo igual y una ese invertida, como la que utilizas en la letra ñ, este símbolo sirve para representar la congruencia, aquí observas que ambos triángulos tienen la misma forma y el mismo tamaño, aunque su posición sea diferente. Ambos son congruentes.
Observa cómo se utiliza la nomenclatura para escribir que esos triángulos son congruentes: ABC DEF
¿Puedes determinar si 2 triángulos son congruentes, sin medir sus lados o ángulos y sin sobreponer uno con otro? Sí es posible, con los criterios de congruencia, pues estos nos sirven para establecer que dos triángulos son congruentes con un mínimo de condiciones Estos criterios son 3, pero en sólo verás uno, el criterio lado-lado-lado, o bien, LLL.
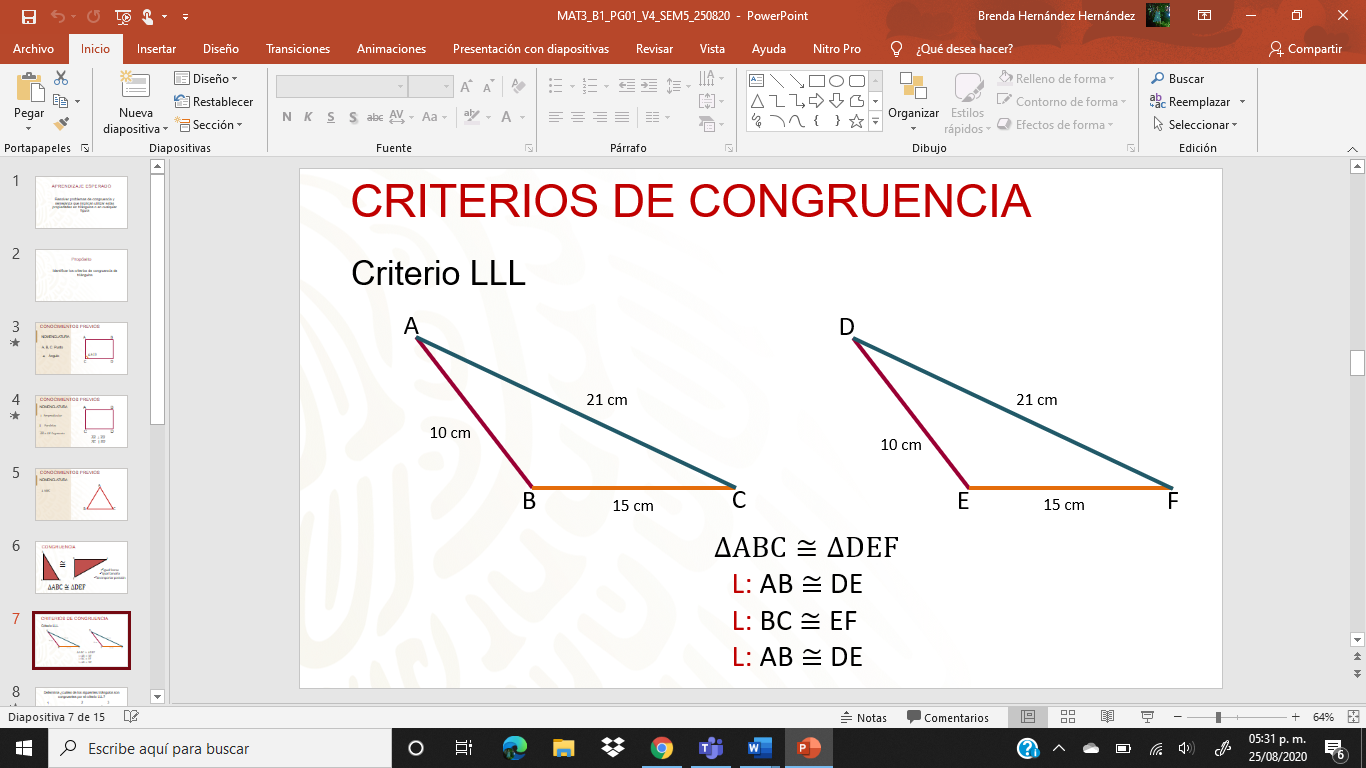
Observa: ¿Serán los triángulos 1 y 2? ¿o serán el 1 y 3? ¿o el 2 y 3? Observa las medidas de los lados y recuerden que para que dos triángulos sean congruentes por LLL, deben tener sus 3 lados homólogos correspondientes iguales.
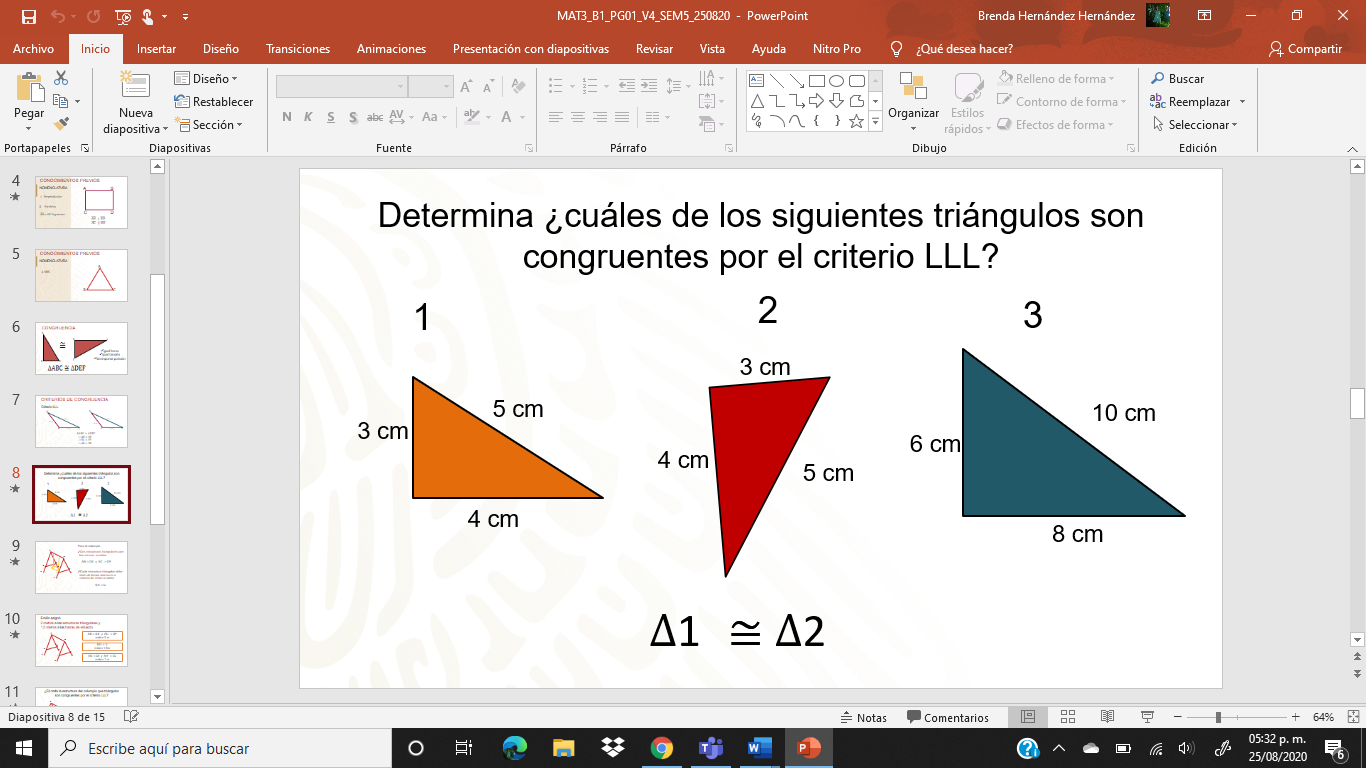
La pareja de triángulos congruentes son el triángulo 1 y 2, pero ¿por qué el triángulo 3 no es congruente con 1 o 2? Es porque, aunque tengan la misma forma, las medidas de sus lados homólogos correspondientes, no son iguales.
Resuelve el siguiente problema:
Gerardo es herrero y le encargaron construir un columpio, para calcular sus costos hizo un esquema y se lo entregó a Emilio su ayudante y le dijo:
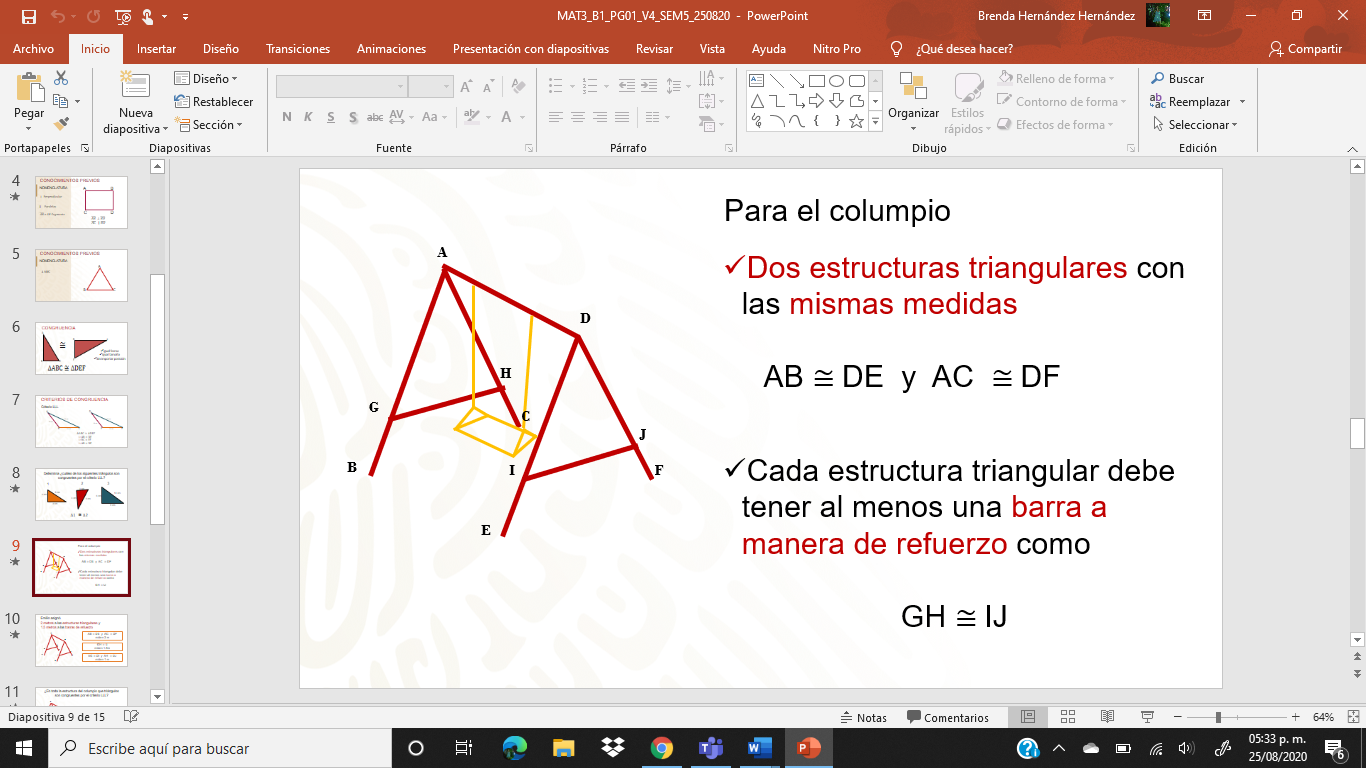
Emilio realizó la siguiente estructura, de acuerdo con la descripción de Gerardo y:
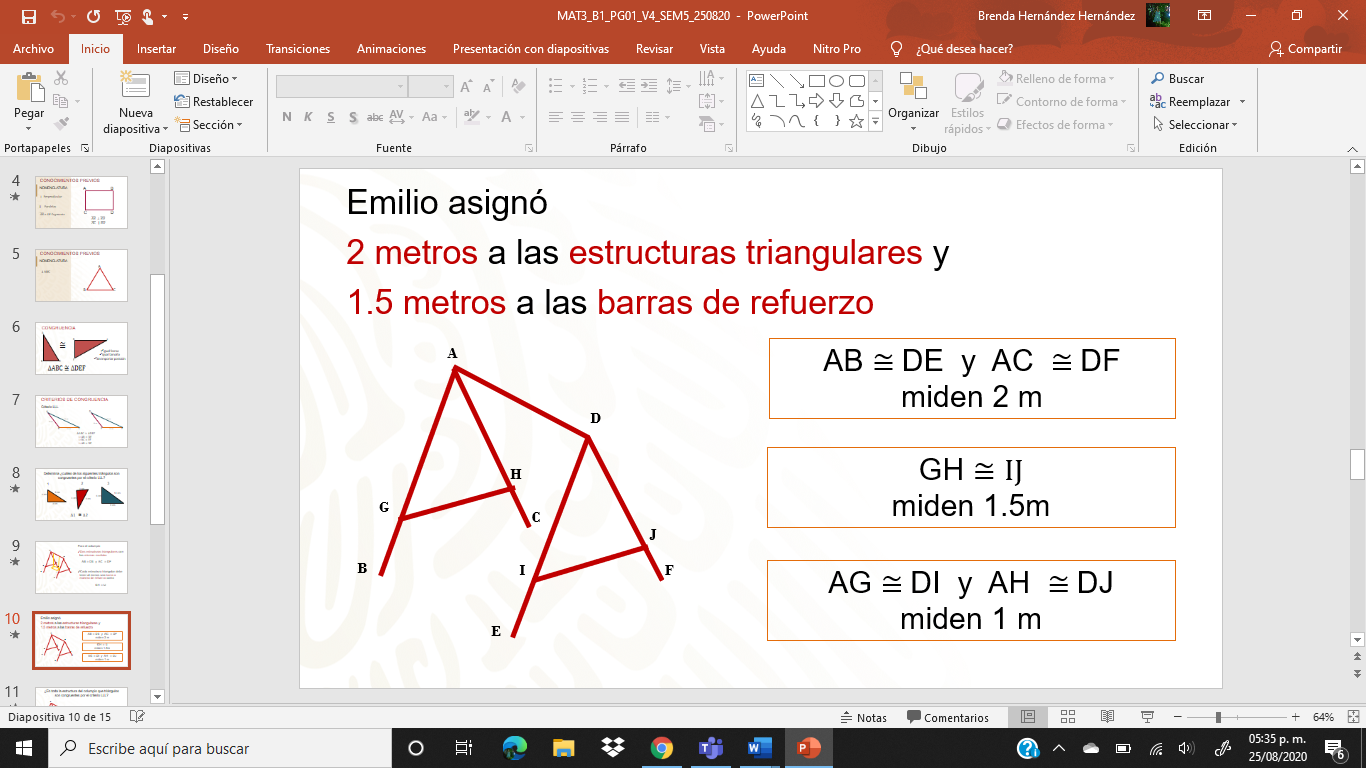
Observa la estructura del columpio ¿Cómo son entre sí las estructuras ABC y DEF, ambos triángulos son congruentes? ¿Podría determinarse que ambos triángulos son congruentes por el criterio LLL?
Sí son congruentes porque, aunque desconoces el valor de CB y de EF, estos deben ser congruentes y paralelos a los soportes JH, IJ de lo contrario el columpio tendría falta de equilibrio o estabilidad.
¿En toda la estructura del columpio encontraste otros triángulos congruentes por el criterio LLL? Observa nuevamente la estructura del columpio.

¿Qué triángulos son congruentes por el criterio LLL?
Así es por que tiene sus tres lados homólogos correspondientes iguales, es decir:
GH
AG DI
AH DJ
Ahora, si alguien dice que, LLL es un criterio de congruencia, también lo es LL. ¿Será eso cierto?
Considera una circunferencia cuyo radio desconoces, C es el centro de la circunferencia y a su vez éste es uno de los vértices de los triángulos ACB y ECD. Observa que CB, CA, CD y CE tienen la misma longitud puesto que estos son a su vez radios de la circunferencia.
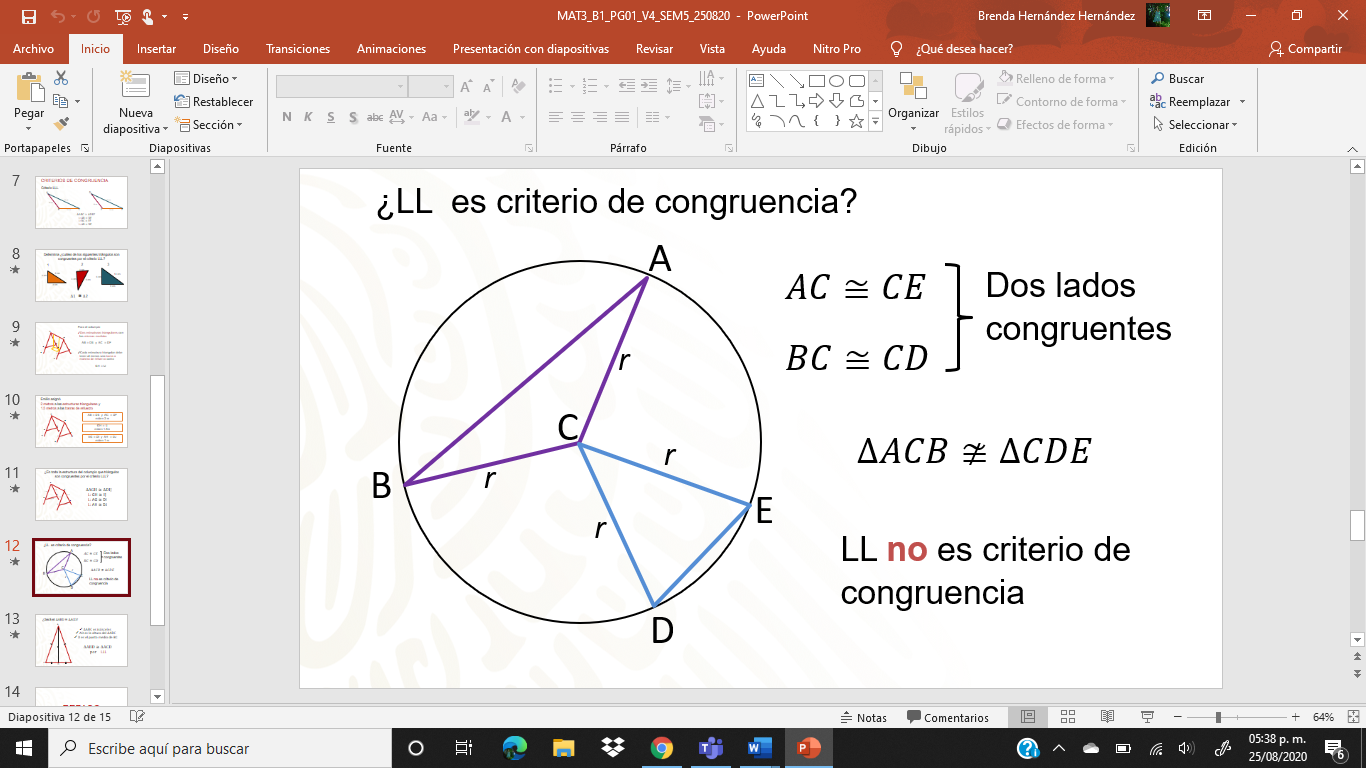
Sin embargo, aunque ambos triángulos tengan 2 lados iguales, estos no pueden ser congruentes ya que su tercer lado homologo correspondiente, que es BA y DE respectivamente, no mide lo mismo. Esto lleva a que LL no es un criterio de congruencia.
Pudiste observar que para probar que LL no es un criterio de congruencia, ocupaste un ejemplo en donde se observó que se cumplía la congruencia de lados, pero no la congruencia de 2 triángulos. Esto es lo que se denomina un contraejemplo, es decir, un ejemplo que prueba la falsedad de un enunciado.
Con esto queda probado que no se puede determinar que 2 triángulos son congruentes por tener 2 lados iguales. Resuelve un último problema:
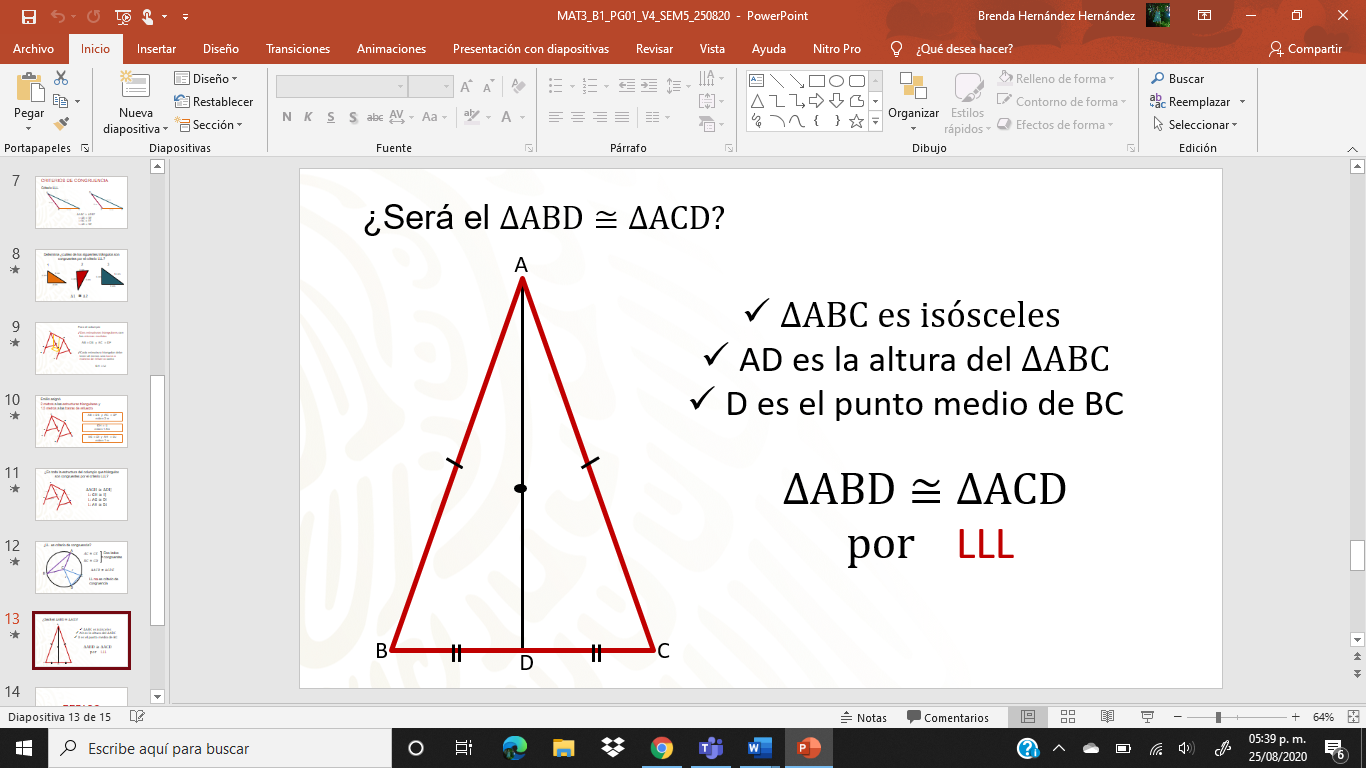
¿Será el ?
La información con la que cuentas es que , recuerda que el triángulo isósceles tiene 2 lados iguales. También te indica que AD es la altura del , sabes que la altura es el segmento que une un vértice con el lado opuesto y ésta a su vez es perpendicular.
Y como último dato indica que D es el punto medio de BC, es decir divide en dos partes iguales al segmento BC. ¿Con la información dada podrías determinar que el triángulo ABD es congruente con el triángulo ACD?
Marca los lados homólogos correspondientes iguales, con base a la información antes dada.
AB es igual AC por ser los lados de un triángulo isósceles
AD que es la altura del triángulo isósceles, que es a su vez lado del triángulo ABD y lado del triángulo ACD. Por último, si D es punto medio de BC, entonces BD y CD son iguales. Por lo tanto, el ABD es congruente con el triángulo ACD por el criterio LLL, es decir tienen sus tres lados iguales.
Ahora observa a tu alrededor. ¿Tienes algunos triángulos cerca o algo que forme la figura de un triángulo?
Si lograste encontrar algunos, pregúntate: ¿Son triángulos congruentes?
Recuerda algunos de los términos aplicados, te sugiero que los escribas en tu cuaderno con tus propias palabras
Nomenclatura: son símbolos para designar elementos de figuras geométricas.
Clasificación de triángulos: Los triángulos son figuras planas de 3 lados, 3 ángulos y 3 vértices, la suma de sus ángulos interiores es 180°, estos se clasifican según sus lados en Equilátero (todos sus lados son iguales), Isósceles (tienen 2 lados iguales) y Escaleno (los 3 lados son distintos).
Según la medida de sus ángulos están el triángulo Acutángulo (tienen los 3 ángulos agudos es decir menor de 90°), Rectángulo (tienen un ángulo interior recto es decir de 90°), Obtusángulo (tiene un ángulo interior obtuso es decir mayor de 90°).
Congruencia: dos figuras son congruentes si tienen las mismas forma y tamaño, sin importar su posición
Criterios de congruencia: Los criterios de congruencia sirven para establecer que dos triángulos son congruentes con un mínimo de condiciones.
Realiza un ejercicio de cálculo mental, recuerda que el cálculo mental es parte fundamental de las matemáticas, ya que es una estrategia para desarrollar el pensamiento numérico y además ayuda a mejorar la concentración y la agilidad mental.
La actividad que realizarás es la siguiente:
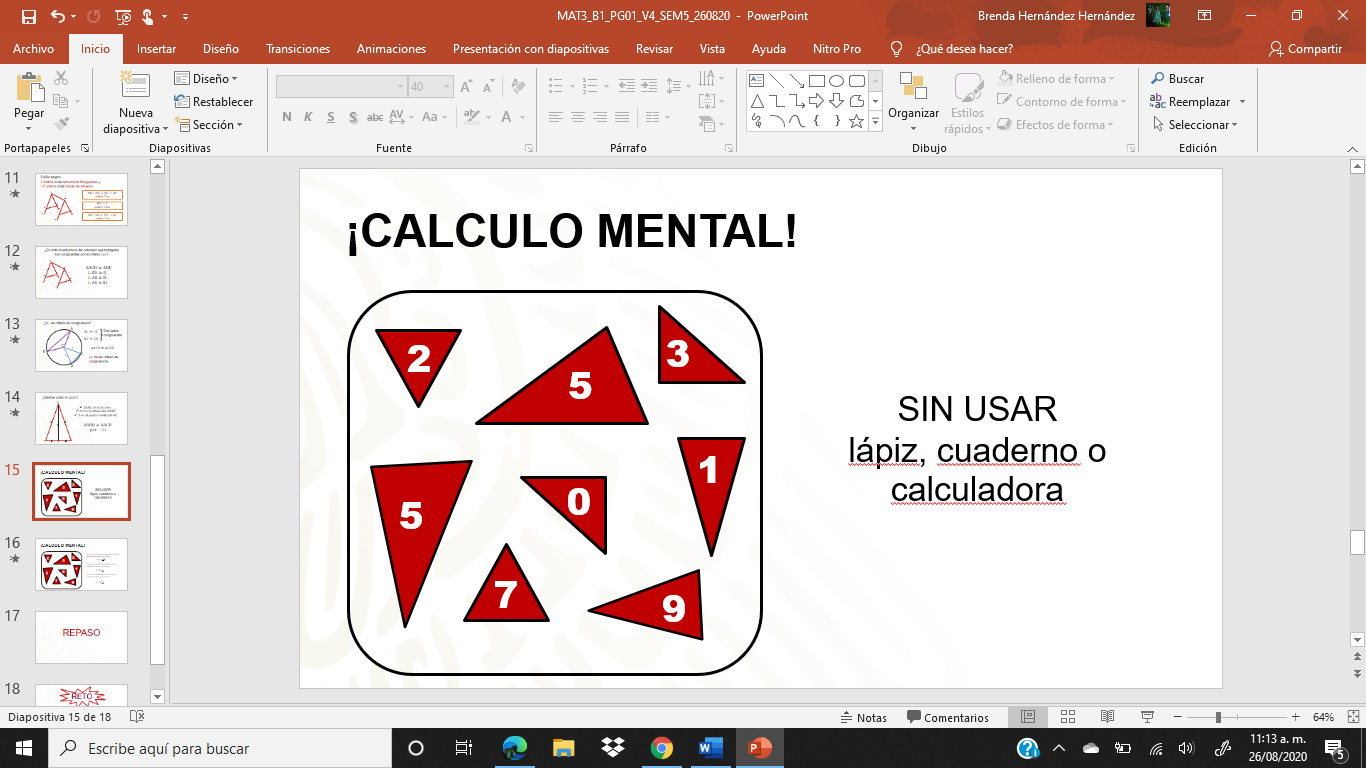
Observa que hay varios triángulos y estos tienen dentro un número.
Multiplica la cantidad que esté dentro de la pareja de triángulos isósceles. Entonces deberás buscar la pareja de triángulos isósceles y realizar la operación, es decir, multiplicar las cantidades que estén dentro de esos triángulos, si observas los triángulos que son isósceles tienen el número 9 y el 1, la respuesta a la multiplicación es 9, ese resultado lo mantendrás guardado en tu mente de modo que cuando leas los siguientes enunciados sumarás los resultados de cada uno de ellos, al final si identificaste los triángulos y realizaste las operaciones correctas, tendrás la misma respuesta. Recuerda que el resultado final es la suma de las respuestas de los enunciados.
Realiza la actividad sin necesidad de usar lápiz, cuaderno o calculadora, esto es cálculo mental.
Multiplica la cantidad que este dentro de la pareja de triángulos equiláteros. ¡Guarda el resultado en tu mente!
Siguiente: Suma la cantidad que esté dentro de la pareja de triángulos rectángulos. ¡Guarda el resultado en tu mente!
Último enunciado: divide la cantidad que este dentro de la pareja de triángulos escalenos. Recuerda que el resultado final es la suma de las respuestas de los 3 enunciados.
¿Lo tienes? El resultado final es 18
¿No obtuviste 18?, observa que sucedió:
Multiplica la cantidad que está dentro de la pareja de triángulos equiláteros
2×7=14
Suma la cantidad que está dentro de la pareja de triángulos rectángulos
3+0=3
Divide la cantidad que está dentro de la pareja de triángulos escalenos
5 5 = 1
Si sumas los resultados de los enunciados, tienes que 14+3+1=18
Cuando tengas oportunidad practica el cálculo mental, ya que mejorarás la concentración y la agilidad mental.
Recuerda que 2 figuras son congruentes si tienen misma forma y mismo tamaño, aunque presenten diferente posición.
Ten en cuenta que existen 3 criterios de congruencia que sirven para establecer que dos triángulos son congruentes con un mínimo de condiciones, y hoy te enfocaste solamente en uno, que es: el Criterio LLL: Dos triángulos son congruentes si tienen los tres lados iguales
Además, usaste un contraejemplo para probar que LL no es un criterio de congruencia.
Observa el siguiente video para consolidar los aprendizajes adquiridos:
- Propiedades de los cuadriláteros
El reto de hoy:
Serán dos retos: el primero:
Por ejemplo, las ventanas, los platos, libros. Anota en tu cuaderno todas las que encuentres, se te sugiere que antes escribas la fecha y el título de la lección, que fue “Congruencia de triángulos”.
El segundo reto, es revisar en tu libro de texto el aprendizaje aprendido, con la finalidad de que profundices en lo aprendido.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: