Comportamiento gráfico de una función lineal
Comportamiento gráfico de una función lineal
Aprendizaje esperado: lee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.
Énfasis: analizar las diferentes representaciones de una relación lineal. Partir del análisis de la gráfica.
¿Qué vamos a aprender?
Analizarás las diferentes representaciones de una relación lineal cuando conoces una de ellas, en este caso, la representación gráfica.
Es importante que, vayas realizando las distintas actividades y ejercicios, así como tomar notas en tu cuaderno de lo que aprendes, además, tus dudas en torno a esta sesión.
Necesitarás: cuaderno, regla y lápiz o bolígrafo.
La pregunta en esta sesión si a partir de una gráfica lineal, ¿puedes obtener la ecuación que define a la línea?
¿Qué hacemos?
La representación gráfica de una ecuación permite hacer una comparación visual rápida para el análisis de una o varias magnitudes con respecto a otra magnitud.
Inicia con la siguiente situación:
Aurelio trabaja en una ensambladora de automóviles y se dedica a conectar el equipo de audio. Para ganar el bono de productividad que otorga la empresa al final de cada mes, debe instalar al menos 132 equipos.
La gráfica muestra cuántos automóviles ha equipado en el mes. Considera que este mes trabajará 22 días y que el trabajo es constante.
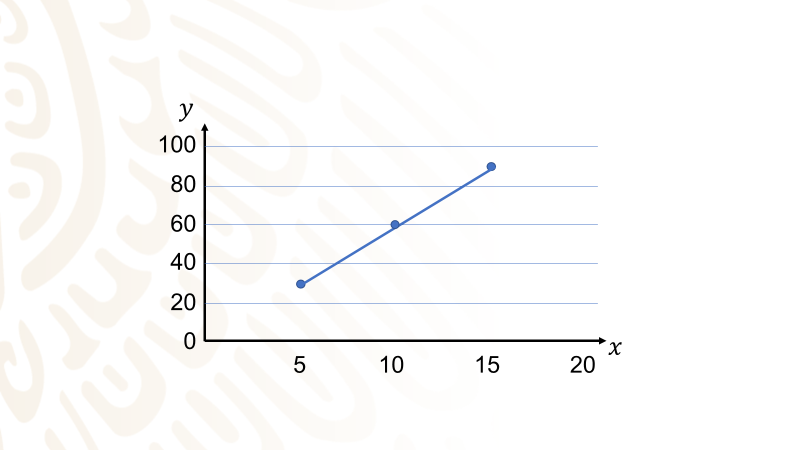
Agrega los títulos correspondientes a la gráfica. ¿Cuáles son esos?
Primero, el título de la gráfica: “Automóviles equipados en el mes”. Luego, el título del eje de las abscisas, que dice lo que mide y cómo lo mide: se mide el mes y es por día.
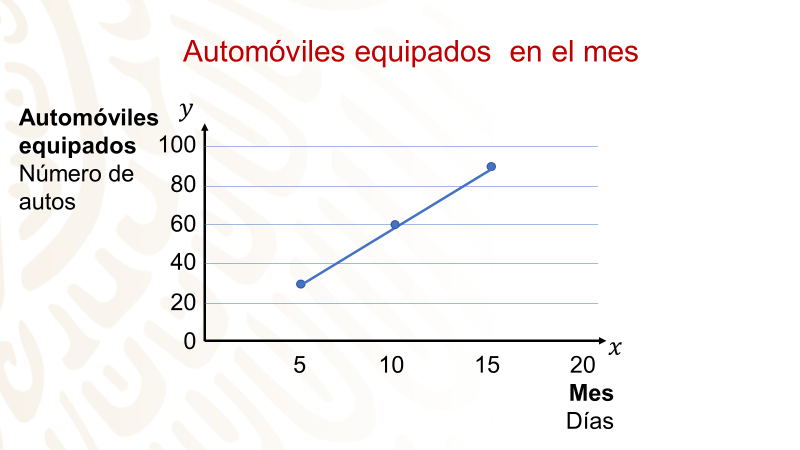
Finalmente, el título del eje de las ordenadas: se miden los automóviles equipados y es por número de equipos.
Según la gráfica y los días que trabajará en el mes, ¿Aurelio llegará a la meta de 132 equipos? ¿A cuántos automóviles les conecta el audio en un día?
Para saber si Aurelio llegará a la meta de 132 equipos, puedes hacer un pronóstico rápido extendiendo la línea hacia arriba y señalando en el eje de las ordenadas el 132.
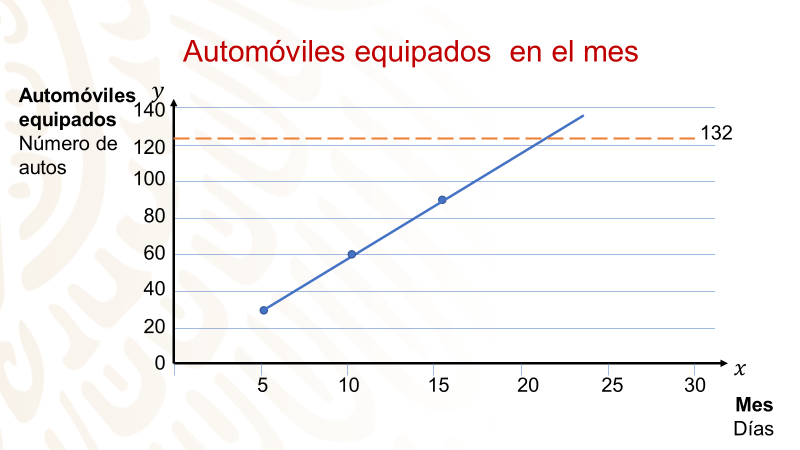
Y parece que Aurelio alcanza la meta. Ahora comprueba si es así. ¿Cómo?, analizando la razón de cambio.
Primero trata de contestar a la segunda pregunta.
Con respecto a la pregunta de cuántos automóviles Aurelio les conecta el audio en un día, localiza las coordenadas que se presentan en la gráfica. ¿Cuáles son?
Se tienen de la gráfica los siguientes datos: a los 5 días ha equipado 30 automóviles, a los 10 días se han equipado 60 automóviles, a los 15 días se han equipado 90 automóviles.
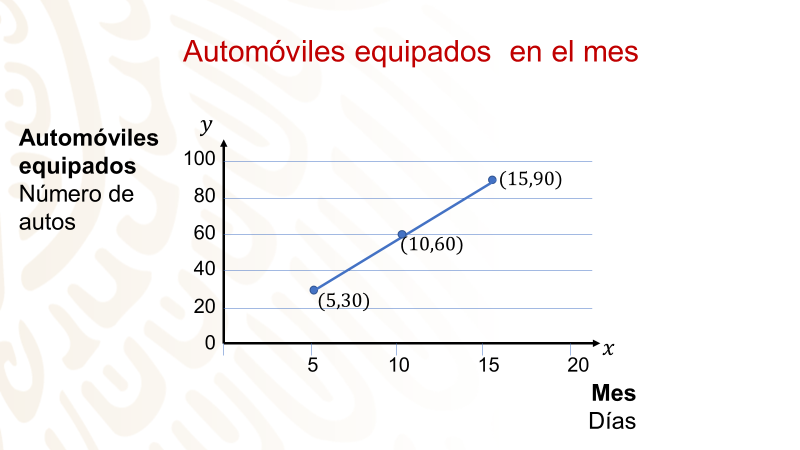
Con los datos conocidos puedes elaborar un registro tabular.
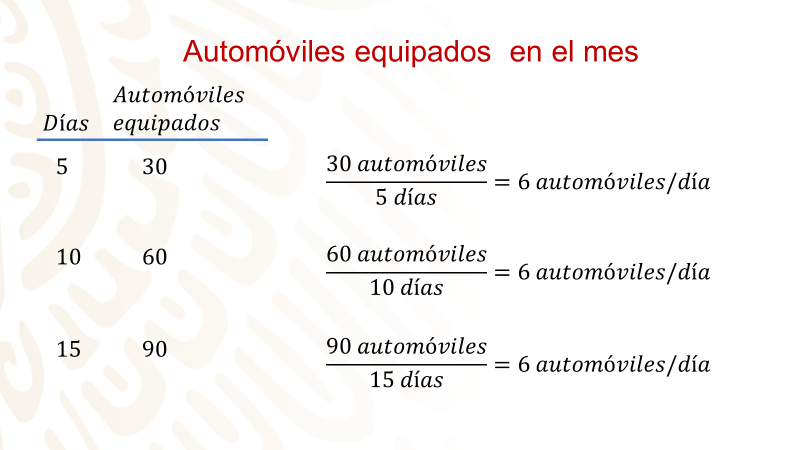
Esto te ayuda a ver la relación que existe entre las dos cantidades: tienes que, si equipan 30 automóviles en 5 días, esto implica equipar 6 automóviles por día. Y esta es la razón de cambio. También con los otros datos se obtiene el mismo resultado.
Ahora, con base en lo anterior, de las siguientes ecuaciones, ¿cuál representa los datos que se encuentran en la tabla?
Las ecuaciones son:
y = 2x + 3
y = 6x
y = 2x – 3
La pregunta, otra vez: ¿cuál representa los datos que se encuentran en la tabla?

Así es: y=6x
Esta ecuación se ajusta a los datos.
Cuando “x” vale 5, “y” es igual a 30.
Cuando “x” vale 10, “y” es igual a 60.
Cuando “x” vale 15, “y” es igual a 90.
Y observas que, para encontrar esta relación, se consideran las dos magnitudes involucradas y la relación que las define, en este caso, la razón de cambio.
Así: y = (razón de cambio) (x)

Entre los resultados que se pueden inferir al encontrar la ecuación, es el valor de “y” cuando x = 0. ¿Cuál es este valor? “0”.
Existen varias situaciones que pueden ser modeladas por este mismo tipo de gráfica y de representación algebraica. Observa:
La siguiente es la gráfica que representa la distancia recorrida (representada con la letra “y”) por una moto de carreras en función del tiempo (representado con la letra “x”). La moto va a una velocidad constante y en determinado momento llega al punto “A” (20, 50)
¿Cuál es el valor de la ordenada del punto cuya abscisa es 20? Es decir, cuando x = 20
¿Y cuándo x = 0? y = 0
¿Cuál es la razón de cambio de la gráfica? Otra forma de preguntar es:
¿Cómo varía la gráfica desde la coordenada (0,0) a la coordenada (20,50)? Esa razón de cambio la llamarás “m”, y es la diferencia de las coordenadas en “y” entre la diferencia de las coordenadas en “x”
Esto es, la diferencia de las coordenadas en “y” es que, de cada coordenada, tomas los valores de “y”, y haces la diferencia, en este caso, es 50-0
De manera semejante, la diferencia de las coordenadas en “x” es que, de cada coordenada, tomas los valores de “x” y haces la diferencia, en este caso, es 20-0
Así, la razón de cambio “m” es igual a 50/20, o lo que es lo mismo, 5/2
¿Cuál es la expresión algebraica que corresponde a esta gráfica?
Con el valor de “m”, tienes que la expresión algebraica que corresponde a esta gráfica es: y = (5/2)x
Resuelve el siguiente crucigrama.
Este es un crucigrama de 6 preguntas. Tres horizontales y tres verticales.
Comienza con la primera pregunta.
Horizontal 1. Considerando la gráfica, se tiene que por 3 playeras se pagan $456, ¿cuánto se debe pagar por 5 playeras del mismo tipo y calidad?
Ya tienes una coordenada. Otra coordenada es responder cuánto es el precio de comprar 0 playeras: es cero.
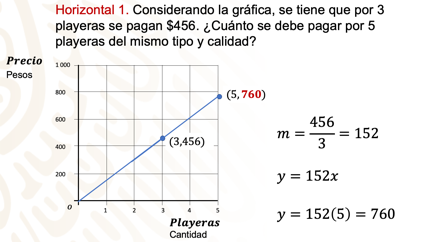
Así, tienes dos coordenadas: (0,0) y (3,456).
“m” es igual a 456/3, que es igual a 152.
Así, la expresión algebraica que define esta situación es:
y = 152x; si x = 5, entonces, el precio a pagar y = 760.
Escribe el resultado.
Resuelta la primera línea horizontal.
Horizontal 2. La gráfica representa una máquina que produce 1 000 tortillas cada 5 minutos, ¿cuántas obtiene por minuto?
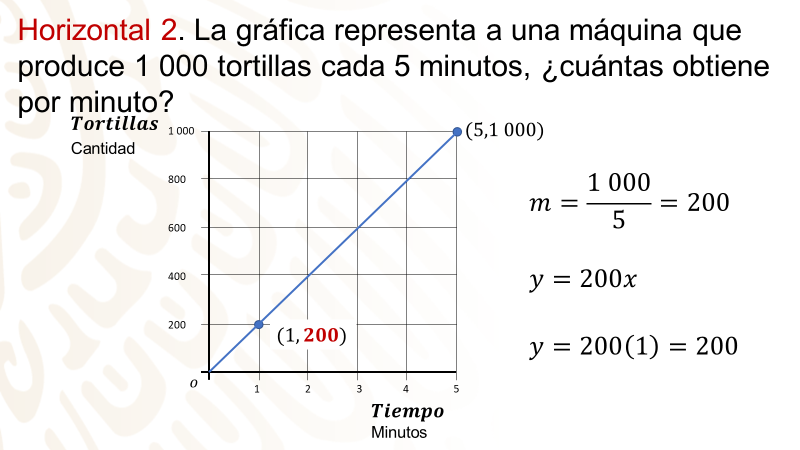
Ya tienes una coordenada; otra coordenada es responder: ¿cuántas tortillas la máquina ha producido cuando el valor del tiempo es 0? Son cero tortillas.
Así, tienes dos coordenadas: (0,0) y (5,1000)
“m” es igual a 1000/5, que es igual a 200
Así, la expresión algebraica es: y = 200x, si x = 1, entonces, y = 200.
La máquina produce 200 tortillas por minuto.
Escribes el resultado en el crucigrama.
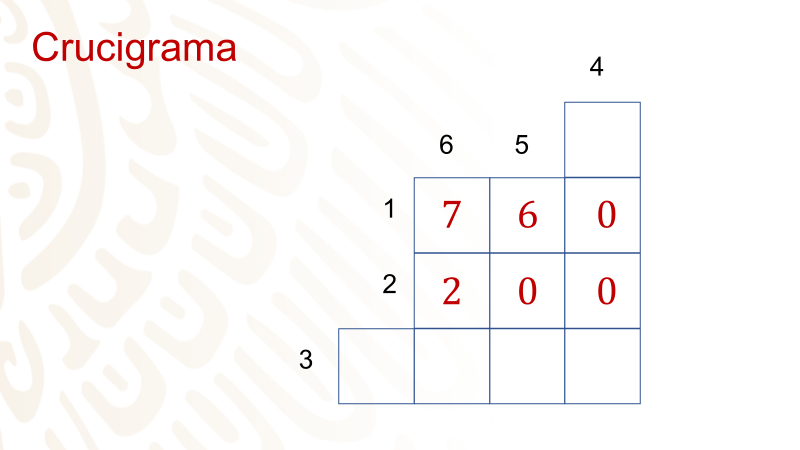
Resuelta la segunda línea horizontal. Pasa a la siguiente.
Horizontal 3. La gráfica representa un terreno que mide 120 metros cuadrados y se paga un impuesto de $950, ¿cuánto se debe pagar por un terreno, en las mismas condiciones, que mide 230 metros cuadrados?
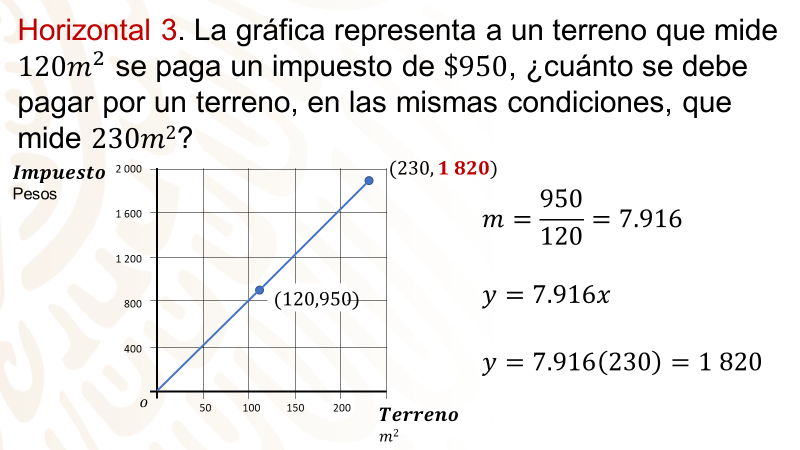
Cuando no se tiene ningún metro cuadrado de terreno, no hay ningún impuesto por ello.
Así, tienes dos coordenadas: (0,0) y (120,950).
“m” es igual a 950/120, que es igual a 7.916.
Así, la expresión algebraica es:
y = 7.916x, si x = 230, entonces, y = (7.916)(230), que es igual a 1 820.
Por un terreno de 230 metros cuadrados se paga de impuesto $1 820.
Escribe el resultado en el crucigrama.
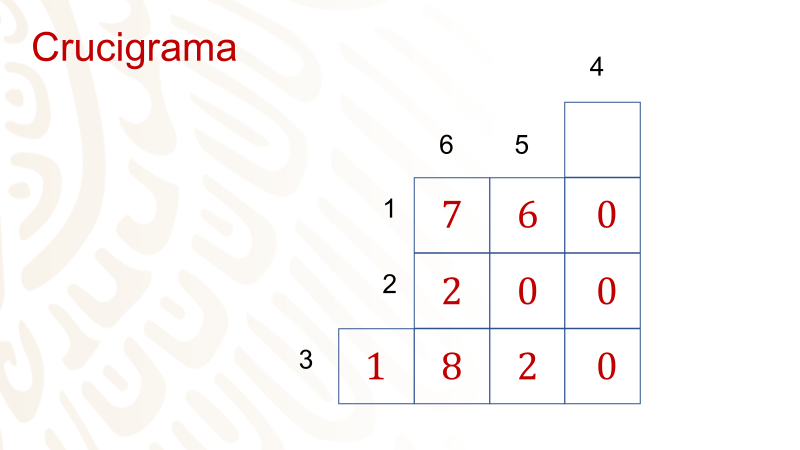
Ya terminaste con las preguntas horizontales. Pasa a las verticales.
Vertical 4. La gráfica representa la producción de 200 focos en 3 minutos, ¿cuántos focos se producen en una hora?
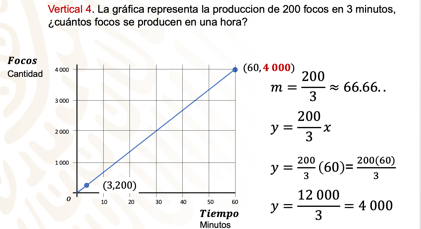
Cuando no se ha empezado a usar la máquina, no hay focos producidos.
Así, tienes dos coordenadas: (0,0) y (3,200).
“m” es igual a 200/3, que es aproximadamente igual a 66.66. Ocuparás la expresión fraccionaria.
Así, la expresión algebraica es:
y = (200/3)x, si x = 60, entonces, y = (200/3)(60) que es igual a 12 000/3, que es igual a 4 000.
Se producen 4 000 focos en una hora.
Escribe el resultado en el crucigrama, pero ahora en las verticales.
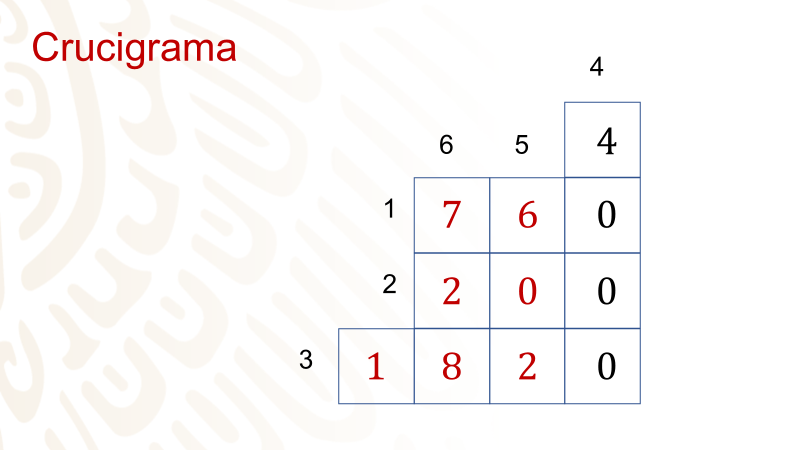
Pasa a la siguiente pregunta.
Vertical 5. La gráfica representa la expresión y=5x. Si y = 3010, ¿cuál es el valor de “x”?
No hay que buscar a “m” como en las preguntas anteriores, pues ya lo tienes.
¿Cuánto vale “m”? 5
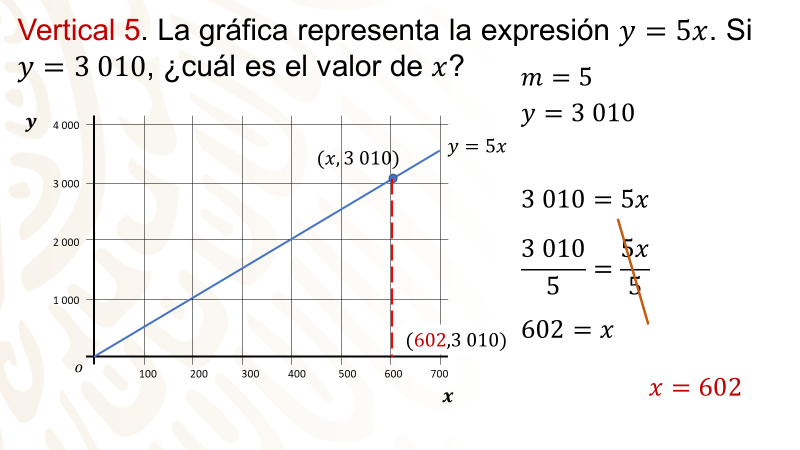
Y también sabes cuánto vale “y”
Para resolver esta pregunta hay que despejar “x”. Establece lo que tienes: 3 010 = 5x
A
ambos miembros de la ecuación los dividirás entre 5 para despejar “x”
Tienes que 3 010 entre 5 es igual a 602 y 5x/5 = x. Así, 602 = x, o lo que es lo mismo: x = 602
Pasa a la siguiente pregunta.
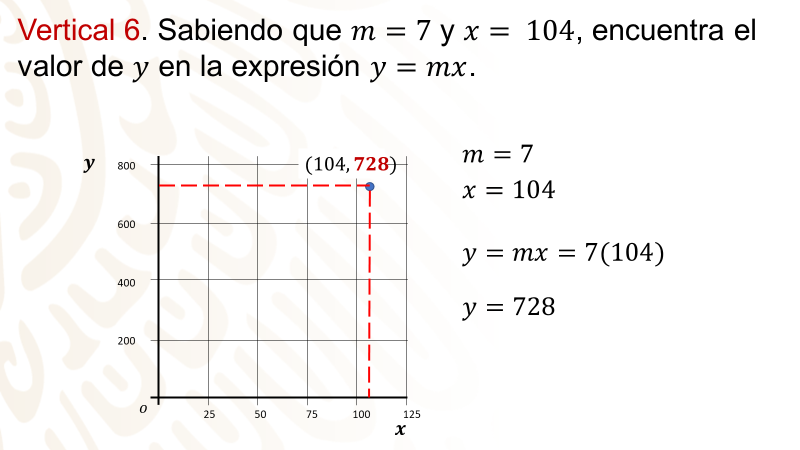
Vertical 6. Sabiendo que m=7 y x=104, encuentra el valor de “x” en la expresión: y=mx
Lo que se pide es encontrar el valor de “y”, con y=mx, y cuando m=7, x=104
Lo que haces es sustituir los valores en la ecuación. Así, y=4(104), que es igual a 728
Observa que el valor obtenido corresponde a lo ya escrito.
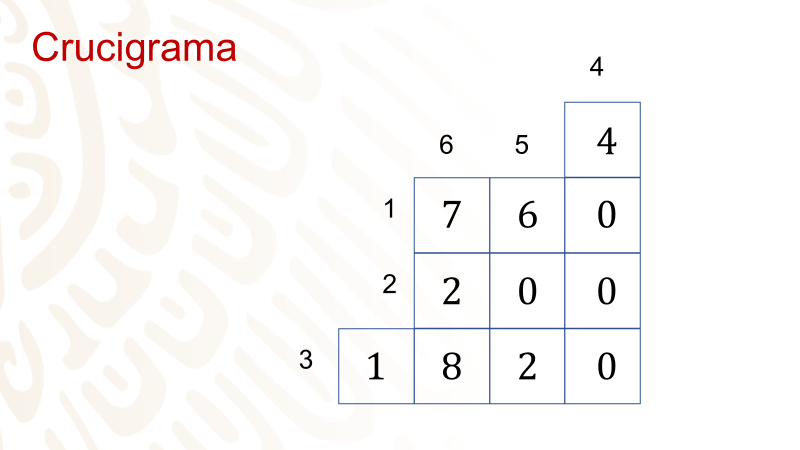
Has completado el crucigrama.
Ahora considera otro tipo de situación. Considera la expresión algebraica de la situación de las edades.
Observa la edad de Luis respecto a la de su hija Diana. Luis tiene 50 años y su hija Diana, 20. ¿Qué edad tenía Luis cuando su hija nació?
La respuesta es una diferencia de edades: la edad de Luis menos la edad de Diana, esto es, 50 menos 20 que es igual 30.
Así, Luis tenía 30 años cuando nació Diana.

¿Qué expresión algebraica representa la relación entre la edad de Luis con respecto a la edad de Diana?
La expresión correspondiente a la situación de las edades se obtiene de que, al restar la edad de Diana de la edad de Luis, se tiene que y-x= 30, es decir: y=x+30

¿Qué significa esta expresión en función de lo que indica el problema?
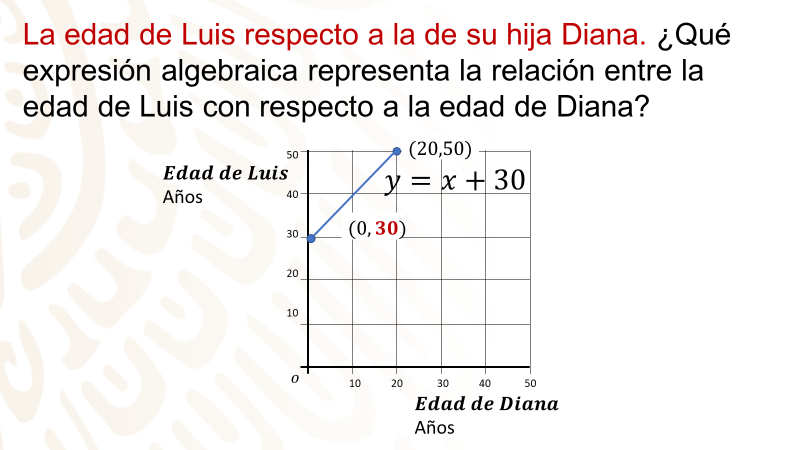
La edad de Luis siempre es mayor que la edad de Diana por 30 años, como se observa en la gráfica. Esta gráfica es diferente a las primeras que consideraste.
Aquí se agrega una cantidad a la ecuación. ¿Qué hace esta cantidad agregada a la gráfica?
Supón que la ecuación sea: y=x ¿Cuánto vale “m”? “m” vale 1. Al sumarle 30, ¿qué pasa con la gráfica?
Observa primero en una tabla. Compara las dos ecuaciones: y=x y y=x+30. Es lo que se esperaba: los valores de “y” aumentan en 30.
Ahora observa las gráficas.
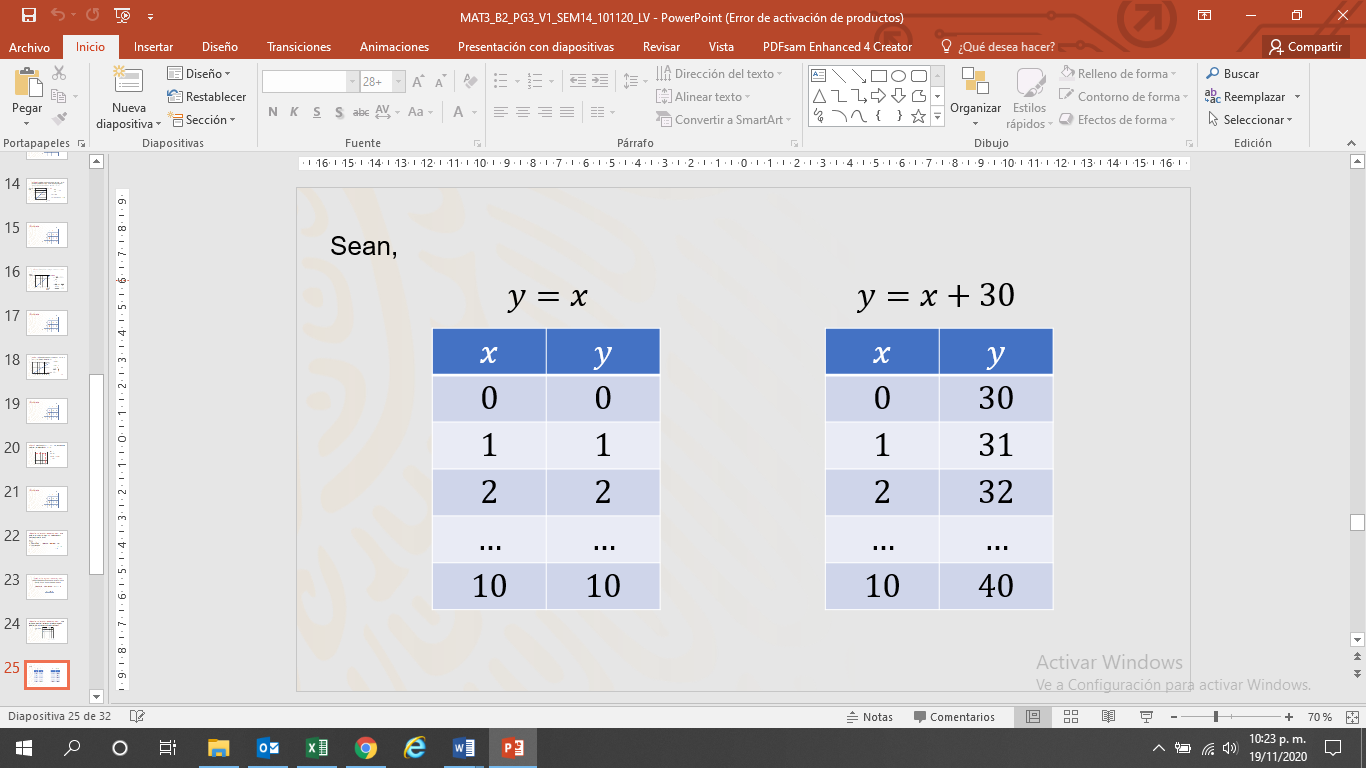
Ambas tienen el mismo valor de “m”; esto es, la relación entre las magnitudes es la misma.
Pero la segunda ecuación, y=x+30, está recorrida en 30 con respecto al eje de las ordenadas.
Mientras en la primera ecuación, cuando la coordenada x=0, la coordenada y=0; en la segunda ecuación, y = 30
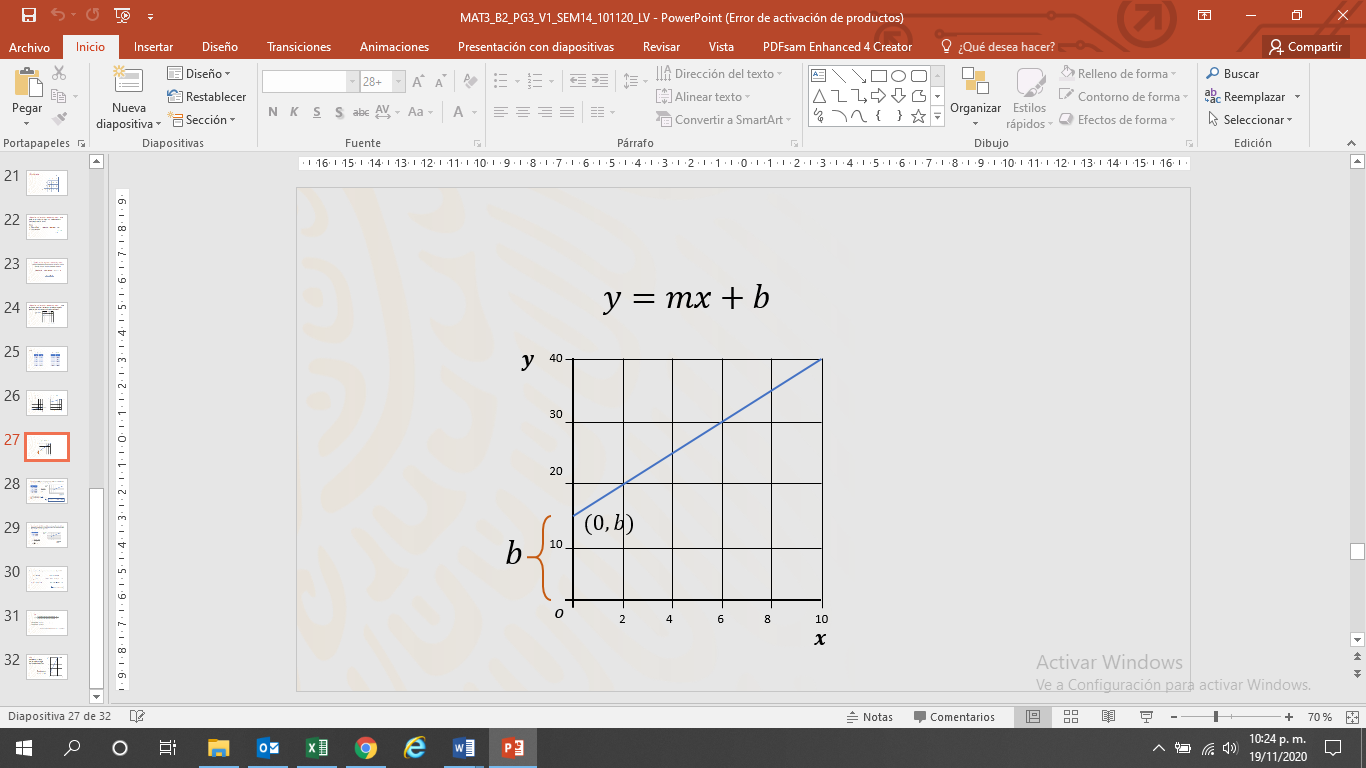
A este tipo de gráficas se les conoce como de la forma y=mx+b, y al valor de “b”, que es la ordenada al origen cuando x=0
+
Un taxi cobra $8.50 por el banderazo (costo fijo al iniciar el viaje) más $3.50 por cada kilómetro recorrido.
La tabla que se presenta a continuación representa esta situación.
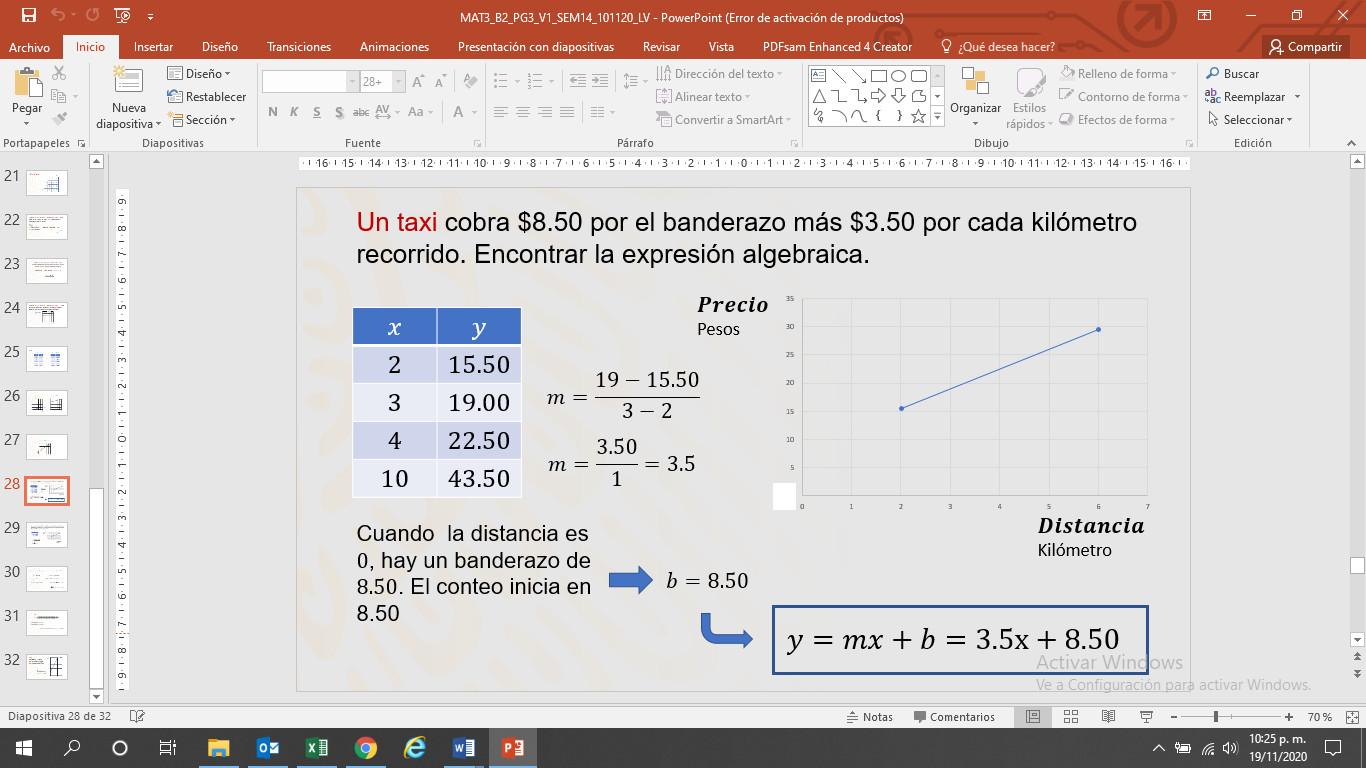
Con los datos de la tabla se puede elaborar la gráfica. Con dos de las coordenadas se puede encontrar la razón de cambio “m”
Así, “m” es igual a la diferencia de la entrada “y” en las dos coordenadas entre la diferencia de la entrada “x” en las dos coordenadas.
Escoge las dos primeras coordenadas: (2,15.50) y (3,19.00)
Entonces, m= (19-15.50) / (3-2), que es igual a 3.50
En la gráfica observas que la línea no pasa por el origen.
El banderazo implica que el conteo no inicia en “0”, sino en 8.50. Esto es: b=8.50
Por lo tanto, la expresión algebraica que representa la situación es:
y=mx + b = 3.5x+8.50
A estos datos y a esta gráfica los puedes asociar a otra situación.
Observa:
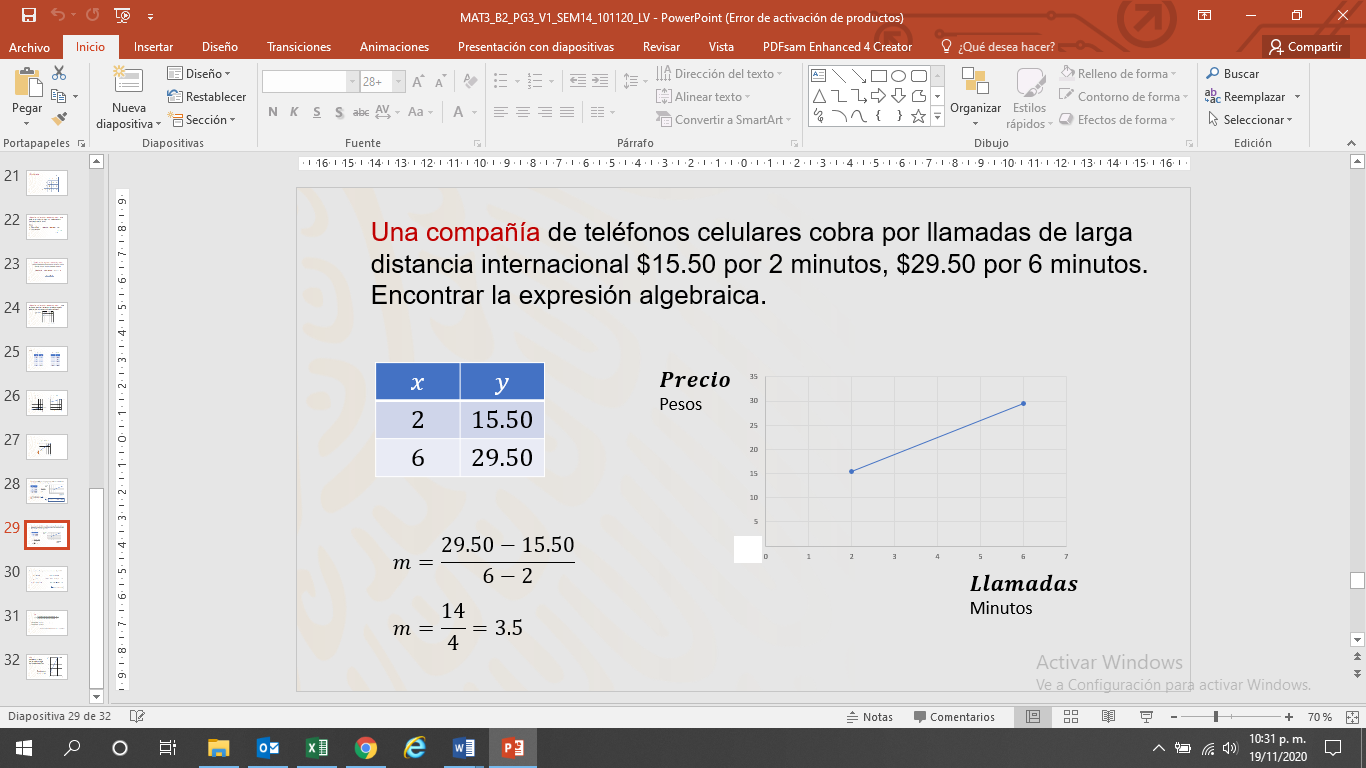
Con los datos de la tabla se puede elaborar la gráfica.
Con las coordenadas se puede encontrar la razón de cambio “m”
Así, “m” es igual a la diferencia de la entrada “y” en las dos coordenadas entre la diferencia de la entrada “x” en las dos coordenadas.
Las dos coordenadas son: (2,15.50) y (6,29.50). Entonces, m= (29.50-15.50)/(6-2), que es igual a 14/4, que es igual a 3.50
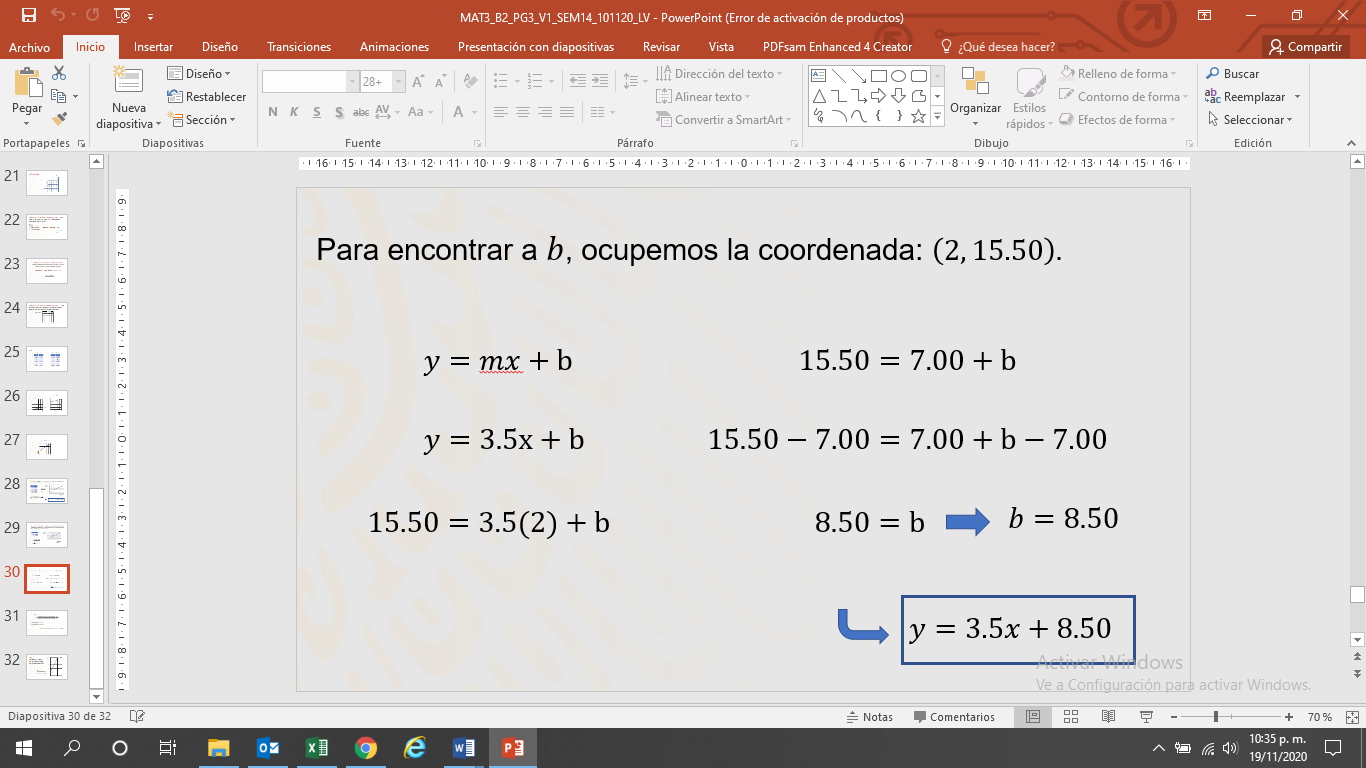
Para encontrar el valor de “b”, considera que ya conoces lo que vale “m” y también el valor de “y” cuando “x” toma el valor de 2 o 6
Entonces, sustituyes a “m” en la forma general: y=mx+b
Entonces, y = 3.5x + b
Toma los valores de la coordenada: (2,15.50). Y sustituye en la forma general:
Entonces, 15.50 = (3.5) (2) + b
15.50 = 7.00 + b
Ahora despeja “b”. En ambos miembros de la ecuación tienes que restar 7, y tienes:
15.50-7 = 7 + b – 7 y 8.5 = b, o lo que es lo mismo, b = 8.50
Por lo tanto, la expresión algebraica que representa la situación es:
y = mx + b = 3.5x + 8.50
¿Te gustaría ver una aplicación de lo que has estudiado en un fenómeno físico?
Observa el siguiente video del minuto 11:21 al 12:49, en donde se menciona otra característica de las gráficas lineales
- Relaciones funcionales, expresiones algebraicas y gráficas.
En el video se hace mención de una gráfica con valores decrecientes. Esto es, cuando se aumenta la variable independiente “x”, la otra variable, la dependiente “y”, disminuye.
Los casos que estudiaste son de gráficas con valores crecientes porque cuando “x” aumentaba, también lo hacía el valor “y”
Observa un poco más de “m”, ya que es una relación entre las dos variables.
En esta sesión definiste a “m” como el cociente de la diferencia de las coordenadas en “y”, y la diferencia de las coordenadas en “x” cuando se tienen dos coordenadas.
Sean:
Coordenada 1 (x1, y1), y
coordenada 2 (x2, y2)
Entonces:
“m” es igual a (y2 – y1)/(x2-x1)
Los casos que estudiaste fueron con “m” positiva.
Todas las gráficas estaban inclinadas a la derecha.
Los otros casos con “m” negativa las verás más adelante.
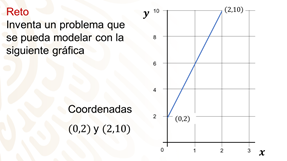
El reto de hoy:
Plantea un problema que se pueda modelar con la siguiente gráfica.
Las coordenadas que se conocen son: (0,2) y (2,10)
Para resolver dudas o ejercitar lo aprendido, te puedes apoyar en tu libro de texto.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: