Áreas
Áreas
Aprendizaje esperado: explora las características y propiedades de las figuras y los cuerpos geométricos.
Énfasis: calcular áreas.
¿Qué vamos a aprender?
La sesión tiene como propósito calcular el área de una figura dentro de otra área, y así alcanzar el Aprendizaje esperado: “Explora las características y propiedades de las figuras y los cuerpos geométricos”
Los materiales que necesitarás es tu cuaderno de apuntes, bolígrafo, lápiz y goma.
¿Cuál es la diferencia entre superficie y área?
¿Qué hacemos?
Una superficie es la región que se tiene por objeto medir, y el área se refiere a su medida, es decir, al tamaño de esa superficie.
Entonces, ¿cuál es la unidad de medida para el área?
La unidad de medida es el metro cuadrado. Por ejemplo, cuando un terreno tiene un área de 10 metros cuadrados, significa que dentro de este caben 10 cuadrados de 1 metro por lado.
Ya sabes calcular el área de algunas figuras geométricas. De este modo, se resuelven problemas calculando el área de dos o más figuras geométricas, considerando la relación que exista entre ellas.
Por ejemplo, cuando la región a medir no es convencional, es decir, que su forma no es geométricamente tradicional sean un cuadrilátero, un triángulo, un círculo o cualquier polígono regular.
¿Cómo se calcula el área de alguna de estas figuras?
Analiza las siguientes situaciones, en las que se debe encontrar el área de la región en color azul.
Observa que hay dos figuras: Un rectángulo delimitado en color verde y un triángulo dentro de él.
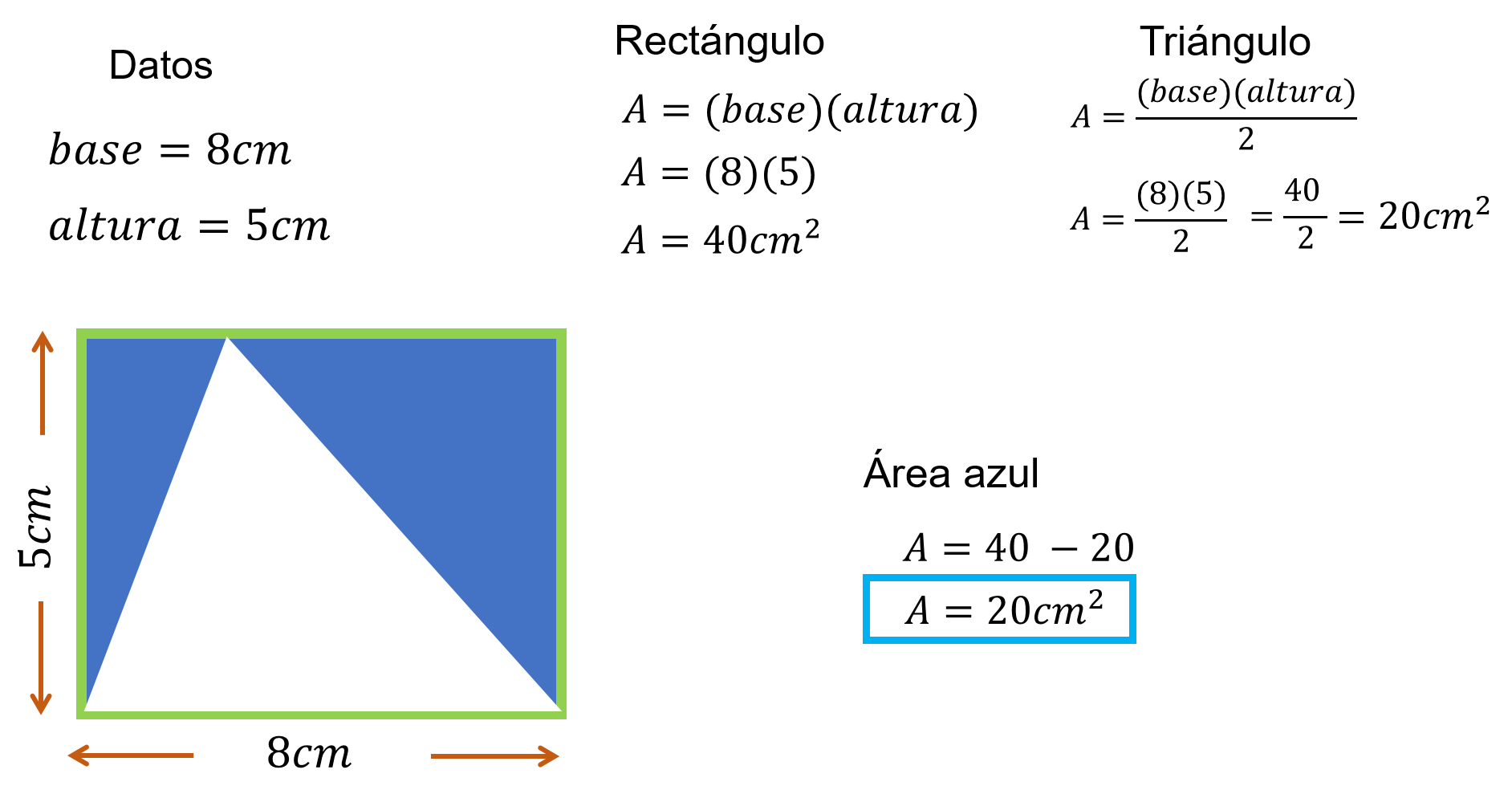
Para calcular el área de la región en color azul, primero se calcula el área del rectángulo para así restarle después el área del triángulo.
Los datos conocidos son: La base del rectángulo y del triángulo igual a 8 cm, y cuya altura en ambas figuras mide 5 cm.
¿Cuál es la fórmula para calcular el área del rectángulo y del triángulo?
El área del rectángulo es igual a base por altura, mientras que, para el triángulo, el área es igual a base por altura entre dos.
De este modo, puedes sustituir los valores en cada fórmula.
Para el caso del rectángulo, el área es igual a 8 por 5, igual a 40 centímetros cuadrados.
Y el área del triángulo es igual a 8 por 5 entre 2.
Al realizar la operación en el numerador, se tiene igual a 40 entre 2, con un área igual a 20 cm cuadrados.
Una vez calculadas las dos áreas, se realiza la resta en donde se ubique primero el área mayor, es decir, la del rectángulo menos el área menor, la del triángulo.
Así, el área sombreada es igual a 40 menos 20, igual a 20 centímetros cuadrados.
Es decir, el área de la región sombreada en color azul es igual a 20 centímetros cuadrados.
Se sabe que hay otras figuras para calcular el área en azul, ¿cuál es la siguiente?
Resuelve a continuación diversos tipos y casos de los cuales se tiene el trapecio ABCD del que se quiere encontrar el área de la región sombreada en color azul.
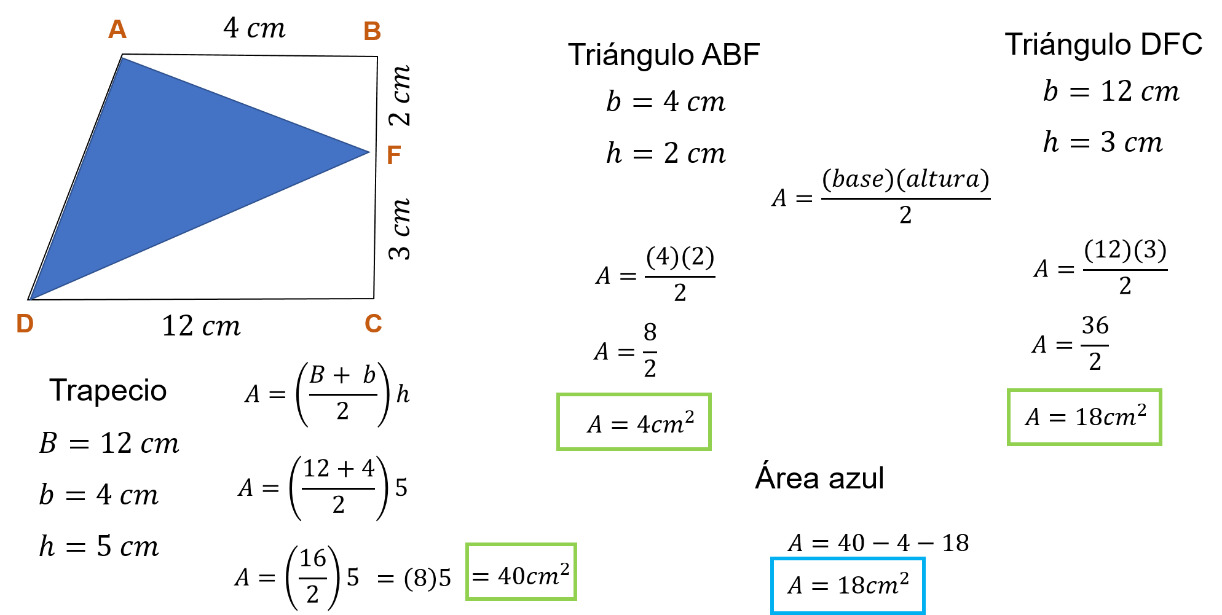
Se sabe que el segmento AB mide 4 cm, el segmento BF mide 2 cm, el segmento FC mide 3 cm y el segmento DC es igual a 12 cm.
Como primer paso, se identifican los datos:
En el trapecio, la base mayor mide 12 cm, la base menor mide 4 cm y la altura mide 5 cm.
Las medidas del triángulo ABF son: 4 cm de base y 2 cm de altura. Y del triángulo DFC, su base mide 12 cm y su altura 3 cm.
Ya sabes que la fórmula para el área del trapecio es igual a base mayor más base menor sobre dos, todo por la altura.
Y para el área de los triángulos es igual a base por altura entre dos.
Después, se calcula el área del trapecio que se le resta el área de los 2 triángulos ABF y DFC, para encontrar el área de la región sombreada en color azul.
Al sustituir los valores en la fórmula del trapecio, el área es igual a 12 más 4 entre 2, todo por 5
Se realizan las operaciones en el numerador, siendo el área igual a 16 entre 2, todo por 5.
Al resolver la fracción, se tiene igual a 8 por 5.
Y finalmente, el área del trapecio es igual a 40 cm cuadrados.
De este modo, se calcula el área del triángulo ABF que, al sustituir en la fórmula, se tiene que el área es igual a 4 por 2 entre 2.
Igual a 8 entre 2 y, por lo tanto, el área del triángulo ABF es igual a 4cm cuadrados.
Se tiene que el área del triángulo DFC es igual a 12 por 3 entre 2, igual a 36 entre 2. Por lo tanto, el área del triángulo DFC es igual a 18cm cuadrados.
Y se continúa para recuperar las áreas obtenidas:
El área del trapecio es igual a 40cm cuadrados; el área del triángulo ABF es de 4cm cuadrados, y el área del triángulo DFC es de 18cm cuadrados.
Y después, se agrupan así: Área del trapecio menos el área de los dos triángulos.
Es decir, 40 menos 4 menos 18, esto es igual a 18cm cuadrados.
Por lo tanto, el área de la región sombreada en color azul es igual a 18cm cuadrados.
Continúa con el siguiente ejercicio.
De nueva cuenta, se debe calcular el área de la región sombreada en color azul.
En esta situación se observan dos rectángulos, uno dentro del otro.

De este modo, se debe calcular el área del rectángulo mayor para restar el área del rectángulo menor.
Los datos conocidos son:
Para el rectángulo mayor, sus dimensiones son: La base es igual a 10cm y la altura es de 6cm.
Para el rectángulo menor, la base mide 4cm y altura 2cm. Y como ya se sabe, la fórmula del área del rectángulo es igual a base por altura.
Como en este caso se tienen dos rectángulos, se genera una única fórmula para encontrar el área de la región sombreada.
Es decir, en la fórmula del área del rectángulo primero se colocan los datos del triángulo mayor menos los datos del triángulo menor.
Entonces, el área es igual a 6 por 10 menos 2 por 4.
Aplicando la jerarquía de las operaciones se resuelven primero las multiplicaciones, seguida de la resta.
En consecuencia, el área es igual a 60 menos 8, teniendo que el área de la región sombreada en color azul es igual a 52cm cuadrados.
Resuelve el siguiente ejercicio.
En el rectángulo ABCD encuentren el área de la región sombreada en color azul.
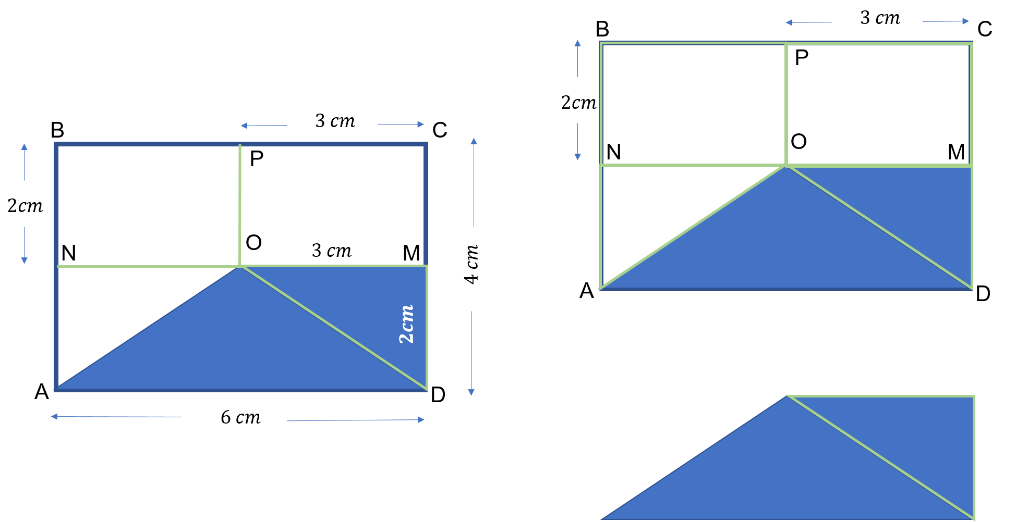
¿Cuáles figuras observas?
Es una imagen en la que, a primera vista, hay dos rectángulos y tres triángulos, pero si observas a detalle las secciones en color azul forman un trapecio.
Podrás encontrar que los dos triángulos sombreados forman un trapecio.
También se observó otro detalle: Las medidas de la base del trapecio y su altura no están explícitas en la figura, pero el segmento PC es igual al segmento OM, así como el segmento BN es igual al segmento MD. Para este caso, ¿los segmentos que son iguales miden lo mismo?
Si el segmento PC mide 3 cm, que es la mitad del segmento AD, que mide 6cm. Por lo tanto, el segmento OM también mide 3cm, que es la base menor del trapecio, y en el caso del segmento BN que mide 2cm, es la mitad del segmento CD de 4cm. Por lo tanto, el segmento MD mide 2cm, siendo éste la altura del trapecio.
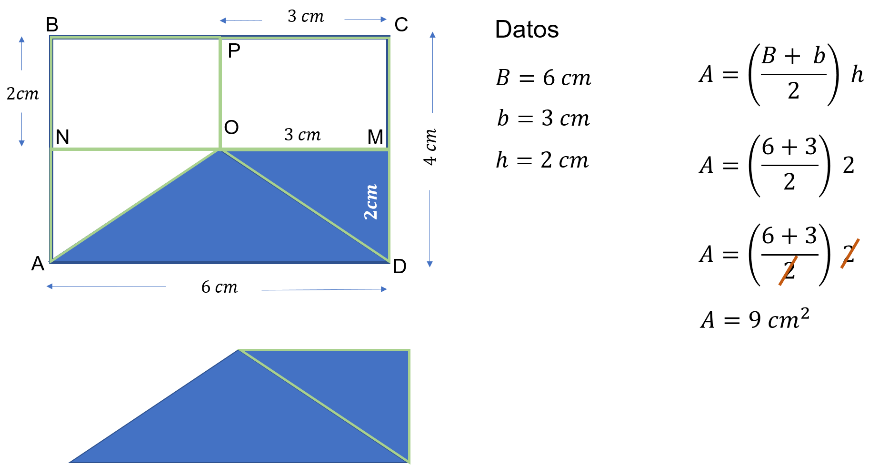
Así, los datos del trapecio son: Base mayor igual a 6cm; base menor igual a 3cm y la altura igual a 2cm.
Para calcular el área del trapecio, es igual a base mayor más base menor entre dos, todo por la altura.
Al sustituir los datos, el área es igual a 6 más 3 entre 2, todo por 2.
Y al analizar las operaciones, en el numerador se tiene que el área es igual a 9 entre 2, todo por 2.
Al eliminar los términos que multiplican y dividen, se tiene que el área es igual a 9 cm cuadrados.
Es decir, el área de la región sombreada en color azul es igual a 9 cm cuadrados.
Observa la siguiente figura y responde:
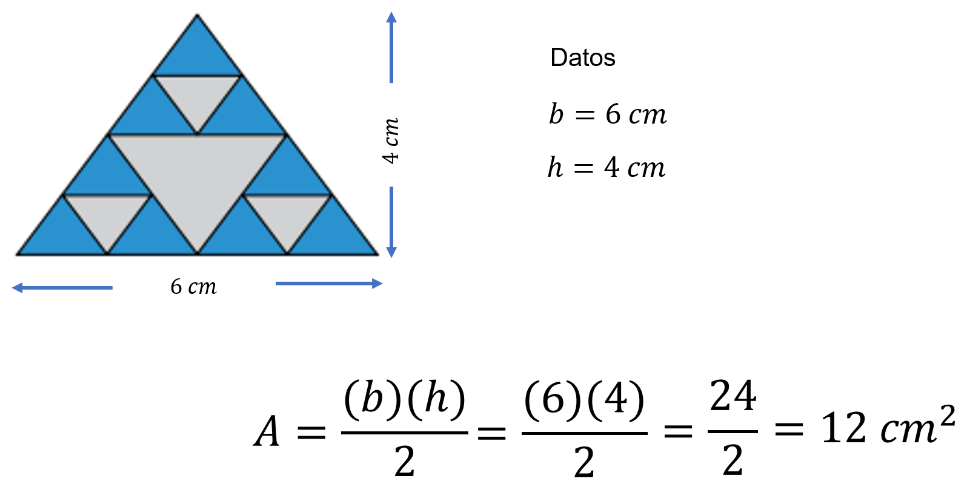
- ¿Cuánto mide el área del triángulo completo?
- ¿Cuánto mide el área de la región azul?
- ¿Cuánto mide el área de la región gris?
Para la primera pregunta, el área del triángulo completo es igual a base por altura sobre dos.
Es decir, 6 por 4, entre 2.
Al realizar las operaciones es igual a 24 entre 2; entonces el área del triángulo completo es de 12 cm cuadrados.
¿Cómo se calcula el área para la región azul? ¿Y cómo para la región gris?
Observa el triángulo gris mayor; éste es una cuarta parte del triángulo completo, es decir, caben cuatro triángulos grises en el triángulo completo.
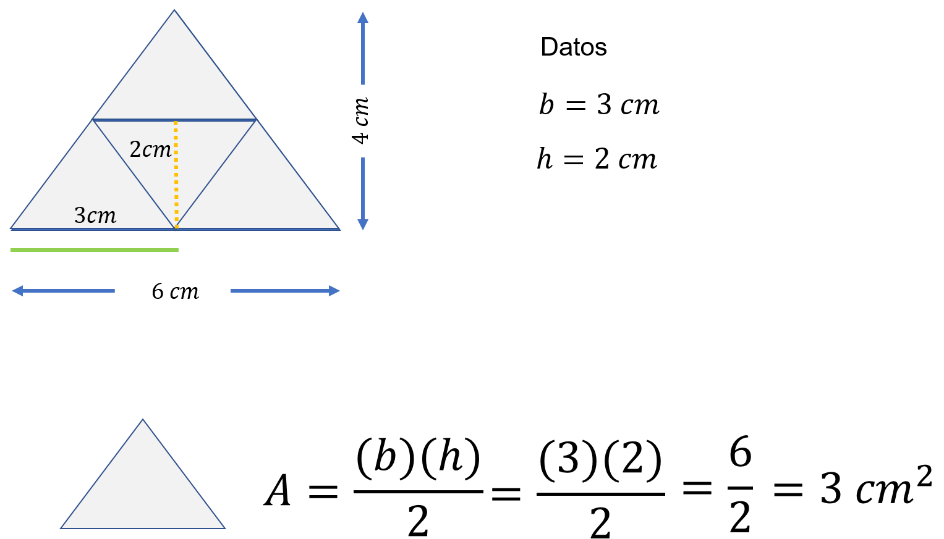
Su base mide 3 cm y su altura es de 2cm.
Pero ¿cuál es el área del triángulo gris?
Si su base mide 6cm y altura 2 cm, entonces el área es igual a 3 por 2 entre 2, que es igual a 6 entre 2.
Entonces, el área del triángulo gris grande es de 3cm cuadrados.
Sin embargo, todavía no es posible calcular el área de la región en azul dado que los triángulos azules son más pequeños.
De acuerdo con el razonamiento de los triángulos grises, se observa que los triángulos azules y los triángulos grises pequeños son iguales, y que éstos caben en un triángulo gris grande.
Entonces, se verifica cuántos triángulos azules pequeños caben en el triángulo gris grande: 1, 2, 3 y 4.
Pero ¿cuál es el área de un triángulo azul pequeño?

Su base ahora es la mitad del triángulo gris, y mide 1.5 cm; su altura también es la mitad del triángulo gris y mide 1cm.
Al realizar las operaciones, se tiene que el área es igual a 1.5 por 1, entre 2, es decir, 1.5 entre 2. Por lo tanto, el área del triángulo pequeño azul es igual a 0.75cm cuadrados.
Observa de nueva cuenta la figura: ¿Cuántos triángulos pequeños azules hay?
Son 1, 2, 3, 4, 5, 6, 7, 8… 9 triángulos azules pequeños en total, maestro.
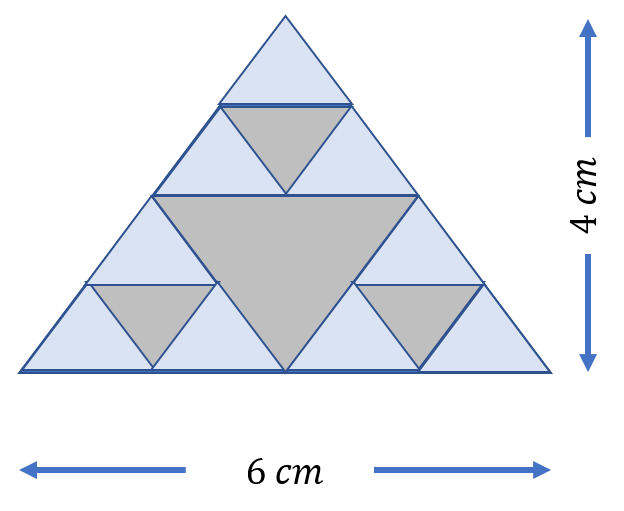
Ya sabes cuántos triángulos pequeños azules son y cuánto mide su área, ¿podrías responder la segunda pregunta?
Porque de este modo, se puede conocer el área de la región azul.
Si son 9 triángulos pequeños azules, y cada uno tiene un área de 0.75cm cuadrados, se multiplica 0.75 por 9 que es igual a 6.75cm cuadrados.
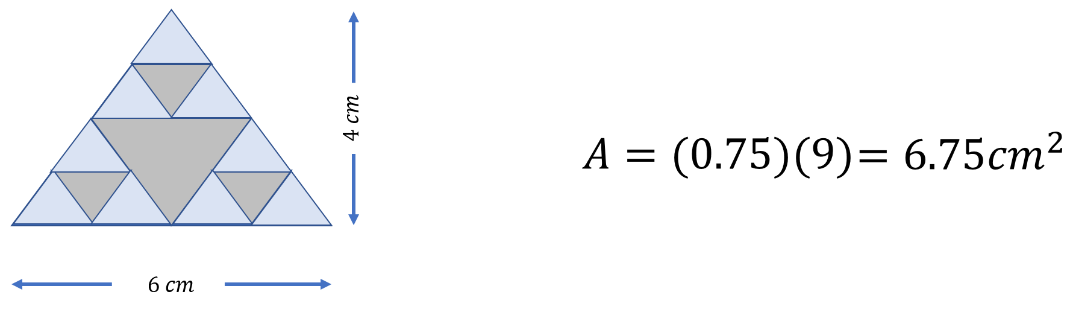
Sólo falta calcular el área de la región gris. Observa cómo se tiene un triángulo gris grande y tres triángulos grises pequeños que son iguales a los triángulos pequeños azules.
Así, el área de toda la región gris se calcula sumando el área de un triángulo grande gris de 3cm cuadrados, y 3 veces el área de un triángulo pequeño de 0.75cm cuadrados.
Es decir, 3 más “3 veces 0.75”, es igual a 3 más 2.25. Por lo tanto, el área de toda la región gris es igual a 5.25cm cuadrados.
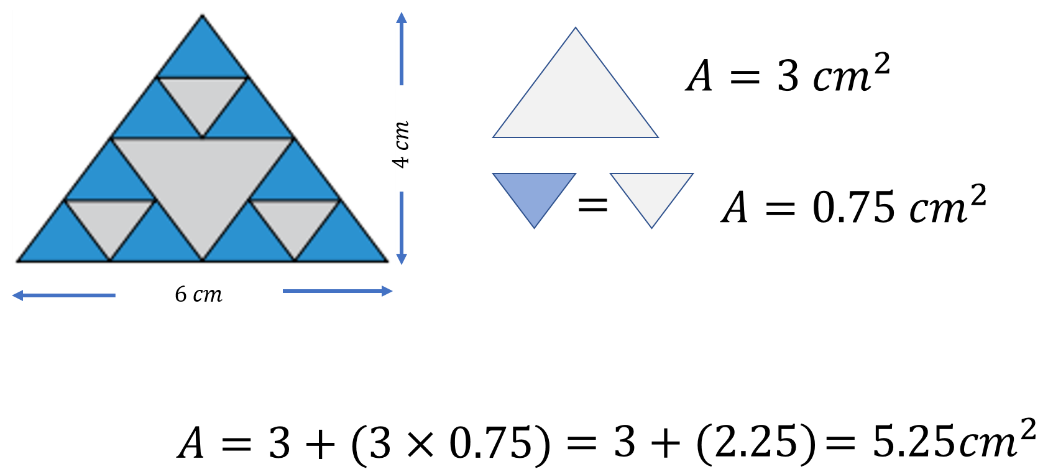
Como podrás darte cuenta el calcular áreas dentro de una figura parecía complejo, pero es cuestión de observar el acomodo de los triángulos y realizar las operaciones adecuadas para conseguir el resultado.
El conocimiento de la geometría permite calcular áreas dentro de otras figuras.
Resuelve otro ejercicio:
¿Cuánto mide el área de la región sombreada en color rojo? Para saberlo, primero se calcula el área del cuadrado y después, se resta el área de los dos semi círculos en color blanco.
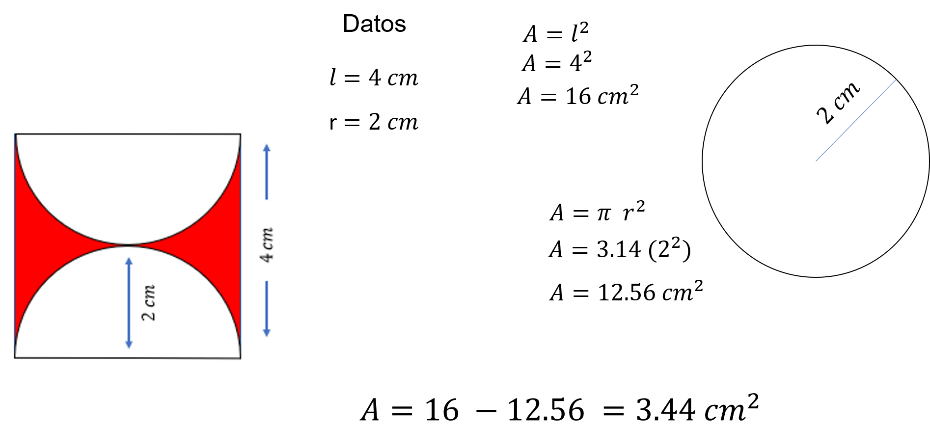
Los datos de la figura son: El lado del cuadrado mide 4 cm; el radio de los semi círculos mide 2 cm.
Al sustituir los valores en la fórmula para calcular el área del cuadrado se tiene:
Que el área es igual a cuatro al cuadrado.
Y elevando el término al cuadrado, el área del cuadrado es igual a 16 cm cuadrados.
Calcula el área de los semicírculos, es posible transportar los 2 semi círculos para formar un círculo completo.
Al aplicar la fórmula y calcular el área de la circunferencia, el área es igual a 3.14 por 2 al cuadrado.
Tras realizar las operaciones, se obtiene que el área de la circunferencia es igual a 12.56 cm cuadrados
Y finalmente, se calcula las diferencias entre el área del cuadrado y el área del círculo: El área es igual a 16 menos 12.56, es decir, el área de la región sombreada en color rojo es igual a 3.44 cm cuadrados.
Analiza el siguiente ejercicio.
¿Cuánto mide el área de la región sombreada en color rojo? En esta ocasión, los datos proporcionados en las figuras son: Lado del cuadrado mide 3 cm; el radio de la fracción de la circunferencia mide 1.5 cm.
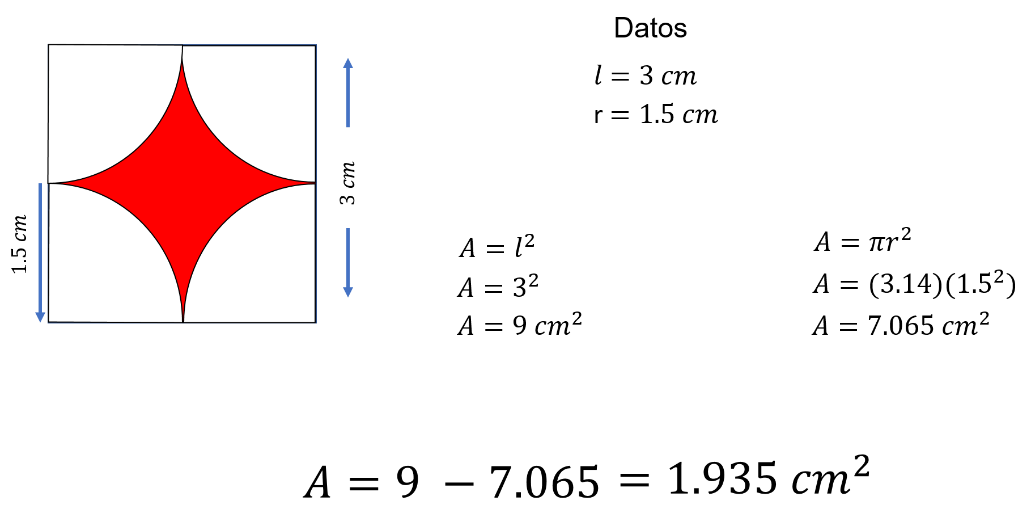
Para calcular el área sombreada en color rojo, se obtiene calculando el área del cuadrado y restándole el área de la región blanca, que está formada por cuatro cuartos de círculo, formando un círculo con diámetro de 3 cm.
Ya con esta información, se puede calcular el área del cuadrado. Al sustituir los datos en la fórmula, el área del cuadrado es igual a 3 al cuadrado. Tras realizar las operaciones, el área del cuadrado es de 9 cm cuadrados.
Observa que las cuatro esquinas del cuadrado —que tienen una cuarta parte de una circunferencia cada una—, forman un círculo completo.
La fórmula para calcular el área de la circunferencia, en este caso, es igual a 3.14 por 1.5 al cuadrado, teniendo como resultado 7.065 cm cuadrados.
Pero ¿cuál es la diferencia entre el área del cuadrado y del círculo?
El área del cuadrado es igual a 9 menos 7.065 del área del círculo, que es igual a 1.935 cm cuadrados.
Y finalmente, el área de la región sombreada en color rojo es igual a 1.935 cm cuadrados.
Observa la siguiente figura y responde.
¿Cuánto mide el área de la figura amarilla?
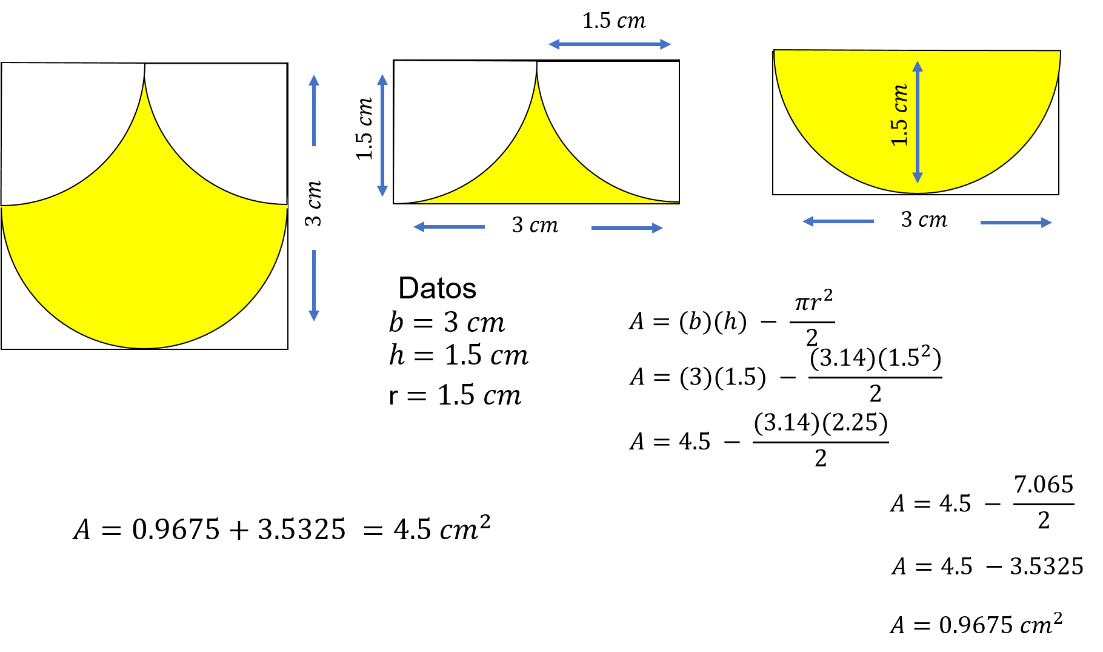
Una sugerencia es dividir el cuadrado de dos mitades con una línea horizontal que pase por el centro del cuadrado.
El área amarilla de la mitad superior del cuadrado es la mitad del cuadrado, menos un medio círculo que se forma al juntar los dos cuartos de círculo.
Y para este caso, los datos son:
La base del rectángulo mide 3 cm; la altura 1.5 cm y el radio de la circunferencia es de 1.5 cm.
Para calcular el área amarilla, se calcula el área del rectángulo formado, menos el área de la circunferencia.
Al sustituir los valores en la fórmula, el área es igual a 3 por 1.5, menos la mitad de la multiplicación de 3.14 por 1.5 al cuadrado.
Al resolver los primeros cálculos, el área es igual a 4.5 menos la mitad de 3.14 por 2.25.
Después se sigue con las operaciones, en la que el área es igual a 4.5 menos la mitad de 7.065
Es decir, 4.5 menos 3.5325.
Por lo tanto, el área de la primera sección superior es igual a 0.9675 cm cuadrados.
El área amarilla de la mitad inferior del cuadrado es un medio círculo. Asimismo, se puede reconocer que el cálculo de este semicírculo ya se realizó en el ejercicio anterior, al calcular la mitad de la circunferencia cuya área es igual a 3.5325 cm cuadrados.
Entonces, el área total de la figura amarilla es el resultado entre la suma del área superior más el área inferior. Es decir, el área es igual a 0.9675 más 3.5325, igual 4.5 cm cuadrados.
Ahora recapitula lo aprendido en la sesión.
Aprendiste a calcular áreas dentro de otras áreas. Es decir, áreas dentro de otras figuras, así como calcular áreas de regiones sombreadas dentro de estas mismas áreas.
Y como condición para realizar los cálculos, se deben de conocer las fórmulas del área de las figuras planas tales como el círculo, el cuadrado, el triángulo, y de otros cuadriláteros como el rectángulo y el trapecio.
Así también, estos conocimientos se aplican en el entorno cotidiano y profesional, por ejemplo: En la arquitectura o ingeniería, para la construcción de una casa, puentes y caminos que mantienen la comunicación en nuestro país.
Asimismo, piensa en qué otras áreas del conocimiento puedes emplear la práctica de las áreas.
Por ejemplo, ¿sabías qué? Desde el año 2000 antes de nuestra era, para evitar las invasiones de los bárbaros del norte, se construyó La Gran Muralla China de más de 6,000 km de longitud y 6 metros de altura. De este modo, ¿podrías calcular el área que tiene semejante estructura?

Asimismo, el astrónomo Johannes Kepler durante el Siglo XVII desarrolló un proceso de integración para calcular áreas y volúmenes relacionados con las leyes del movimiento planetario. Estos conocimientos le permitieron calcular, gracias a las observaciones de Tycho Brahe, la trayectoria de Marte en 1600.

Y como una situación adicional, en la ciudad de Cancún, uno de los principales centros turísticos de México y el mundo, es además una parte importante para la generación de empleos.

Entre las muchas actividades que se realizan, está la del mantenimiento a las albercas de casas y hoteles. Pero podrías pensar en las distintas áreas que cubre cada una de estas albercas.
Como se hace notar, el cálculo de las áreas ha favorecido los avances del ser humano en distintas disciplinas, apoyados de las Matemáticas, y en distintos escenarios sin importar su ubicación.
Por ello, es indispensable la práctica de las matemáticas, y hacer frente a las necesidades que se manifiestan en el presente.
El reto de hoy:
Resuelve otros casos planteados en tu libro de texto de Matemáticas, en el que encontrarás nuevas situaciones para poner en práctica tus conocimientos.
¡Buen trabajo!
Gracias por tu esfuerzo.