Aplicar procedimientos para dividir fracciones
Aprendizaje esperado: resuelve problemas de multiplicación y división con fracciones y decimales positivos.
Énfasis: multiplicar por el recíproco.
¿Qué vamos a aprender?
Aplicarás diferentes procedimientos para dividir fracciones en la resolución de problemas.
Desarrollarás tu pensamiento matemático, y profundizarás en cómo usar el procedimiento adecuado, según el problema multiplicativo que se te plantee.
¿Qué hacemos?
A continuación, observa algunos procedimientos para realizar la división de una fracción entre otra fracción.
Procedimientos para dividir fracciones.
Primer procedimiento.
El primer procedimiento es el de producto cruzado.
En el ejemplo “siete quintos entre tres medios” hay que tomar el numerador de la primera fracción y multiplicarlo de manera cruzada por el denominador de la segunda fracción. El producto se coloca en el numerador.
Después, se procede a multiplicar el denominador de la primera fracción por el numerador de la segunda fracción y el producto se coloca en el denominador.
El resultado es catorce quinceavos, que es una fracción propia.
Segundo procedimiento.
El segundo procedimiento es el conocido como “extremo por extremo y medio por medio”.
Si se sigue la lógica de que se trata de una división, primero se coloca “siete quintos” como numerador y “tres medios” como denominador.
Con este método, una vez que los acomodas, multiplica de extremo por extremo, colocando el resultado del producto en el numerador.
Después se multiplica medio por medio, y se coloca el resultado del producto en el denominador.
El resultado es la fracción propia “catorce quinceavos”.
Tercer procedimiento.
El tercer procedimiento es “el recíproco de la segunda fracción”.
Como aprendiste en la sesión anterior, dividir es lo mismo que multiplicar por el recíproco.
Para saber el resultado de una división de fracciones, se puede multiplicar el dividendo por el recíproco del divisor.
El recíproco de “tres medios” es “dos tercios”; se cambia la fracción y el signo de dividir, y se reemplaza por el signo de multiplicar.
Ahora, se multiplica siete por dos, y cinco por tres, y se obtiene el mismo resultado que con los procedimientos anteriores “catorce quinceavos”.
A continuación, profundizarás en lo siguiente: la división de una fracción entre un entero.
Procedimiento para dividir una fracción entre un entero.
Usa como ejemplo: “nueve cuartos entre tres”.
En este caso, el tres es el número entero: para representarlo como fracción, se le agrega un “uno” en el denominador; ya que tres entre uno es tres, ambas expresiones son equivalentes.
Ahora, como puedes ver, tienes una división entre fracciones.
Para resolverla, puedes usar los mismos procedimientos que aprendiste anteriormente.
Primer procedimiento.
En el primero, se multiplica de manera cruzada el numerador de la primera fracción por el denominador de la segunda fracción y el producto se coloca en el numerador. Después, se procede a multiplicar el denominador de la primera fracción por el numerador de la segunda fracción, y el producto se coloca en el denominador.
Con esto, obtienes como resultado “nueve doceavos”, que se puede simplificar, sacando la tercera parte de nueve y de doce, lo que da como resultado tres cuartos, una fracción propia.
Segundo procedimiento.
Si se usa el segundo procedimiento, se coloca nueve cuartos como numerador y el tres como denominador. Recuerda que debes escribir el tres como fracción, es decir, “tres sobre uno”.
Se multiplican los valores que están en los extremos, y el resultado del producto se coloca en el numerador. En este caso, se multiplica “nueve por uno”, y el resultado, nueve, se coloca en el numerador.
Después, se multiplican los valores que están en medio, y el resultado del producto se coloca en el denominador: “cuatro por tres igual a doce”; se coloca el “doce” en el denominador, y obtienes como resultado “nueve doceavos”, simplificando, se obtiene “tres cuartos”.
Tercer procedimiento.
Con el tercer procedimiento, del “recíproco de la segunda fracción”,
para dividir “nueve cuartos entre tres”, hay que multiplicar “nueve cuartos” por el recíproco de “tres”, es decir por “un tercio”.
Se multiplica nueve por uno, y se coloca el resultado “nueve” en el denominador; “cuatro por tres” da “doce”, y se coloca en el denominador. Simplificando el resultado “nueve doceavos”, se obtiene nuevamente “tres cuartos”.
Ahora estudiarás una nueva variante: la división de un decimal entre una fracción.
Procedimiento para dividir un decimal entre una fracción.
Usa como ejemplo lo siguiente:
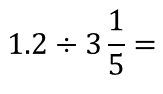
Primero, convierte el número decimal, en este caso 1.2, a fracción, para operar con fracciones.
Escribe el 12 en el numerador y lo divides entre 10, porque se tiene una cifra a la derecha del punto decimal, es decir, décimos.
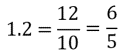
Después, simplifica la fracción 12/10 en este caso. Le saca la mitad al 12 y al 10, ya que el 2 es divisor de ambos, y queda la fracción 6/5.
Luego, convierte 3 1/5 a fracción impropia. Como ya sabes, el 5 multiplica al 3 y se le suma 1, lo que da como producto 16/5.
Ahora ya tienes los dos números en fracciones.
A continuación, realiza lo siguiente:
Actividad.
Concluye la operación anterior, 6/5 entre 16/5, usando los tres procedimientos que aprendiste anteriormente.
Procedimiento 1, producto cruzado.
Procedimiento 2, extremo por extremo y medio por medio.
Procedimiento 3, el reciproco de la segunda fracción.
Anota todas las operaciones necesarias y verifica tus resultados de los tres procedimientos para dividir fracciones.
El reto de hoy:
Realiza otros ejercicios de división de fracciones que se encuentren en tu libro de texto y comparte tus aprendizajes con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/













