Aplicación de los criterios de semejanza de triángulos
Aplicación de los criterios de semejanza de triángulos
Aprendizaje esperado: resuelve problemas de congruencia y semejanza que implican utilizar estas propiedades en triángulos o en cualquier figura.
Énfasis: aplicar los criterios de semejanza de triángulos.
¿Qué vamos a aprender?
Resuelve problemas de congruencia y semejanza que implican utilizar estas propiedades en triángulos o en cualquier figura.
Anteriormente aprendiste sobre congruencia y semejanza de figuras, especialmente de triángulos y cuadriláteros, pero… ¿dónde puedes utilizarlos en tu día a día?
Conocerás uno de los tres criterios de congruencia de triángulos, el que se conoce como Ángulo-Ángulo haciendo un énfasis en la relación de proporcionalidad de sus lados.
Comenzarás con un repaso del tema proporcionalidad, que te brindará información importante antes de entrar al contenido central.
Consideras un segmento de recta al cual denominarás segmento “a” y tiene una longitud de 10 centímetros, y de él mismo, desprendes otro segmento al cual llamarás segmento “b”, y que al copiar del segmento “a” como consecuencia mide también 10 cm de longitud, ambos segmentos son congruentes entre sí ya que tienen la misma forma y tamaño. Comprueba esto matemáticamente hablando: si obtienes el cociente de la medida de ambos segmentos, es decir, 10 centímetros que mide el segmento “a” entre los 10 centímetros que mide el segmento “b” obtienes como cociente el número 1.
Con esto puedes determinar que el segmento “a” es congruente con el segmento “b”, ya que el cociente obtenido de la división de sus medidas te da como resultado 1. Ahora, si aumentas el tamaño del segmento “b” al doble, es decir, en lugar de medir 10 centímetros ahora mide 20 y si realizas el mismo proceso para obtener el cociente encontrarás que 20 entre 10 nos da como resultado 2, es decir que el segmento “a” es el doble del segmento “b” y, por lo tanto, son proporcionales entre sí, ya que tienen las mismas características, pero la medida de uno es el doble de la medida del otro porque el cociente obtenido es mayor a 1.
Ahora al segmento “b” lo reduces hasta llegar a 5 centímetros y realizas la misma operación matemática, encontrarás que 5 entre 10 nos da como resultado 0.5, es decir que el segmento “b” es la mitad del segmento “a” porque el valor obtenido es menor a uno, es decir el segmento resultante es más pequeño.
Estos valores que encuentras al dividir las medidas de los segmentos es el factor constante de proporcionalidad o razón de proporcionalidad.
Cuando el valor del factor de proporcionalidad da como resultado uno, nos indica que ambas líneas son congruentes, es decir que tienen las mismas características y la misma medida, pero si el valor es mayor te indica que las líneas son semejantes ya que tienen las mismas características, pero una es mayor que la otra, si el resultado del coeficiente de proporcionalidad es menor a uno, te indica que la línea comparada es más chica por lo tanto también son semejantes, ya que conservan la misma figura.
Te sugerimos anotar la idea principal de este repaso, ya que con esta información te será más fácil comprender la semejanza en figuras más complejas.

Puedes observar los valores de proporcionalidad obtenidos y podrás comprobar que: cuando el factor constante de proporcionalidad es igual a uno las medidas obtenidas son congruentes, ya que tienen el mismo tamaño. Pero cuando el factor de proporcionalidad es mayor a uno, debes comprender que la figura con la cual se comparó es mayor que la figura original, es decir, es más grande, por lo tanto, son semejantes.
Al contrario, si el factor de proporcionalidad disminuye la figura comparada es más pequeña que la original. Por lo tanto, también es semejante.
La idea es que hayas recordado el concepto de proporcionalidad y hayas anotado la idea principal.
Continúa ahora con figuras un poco más complejas: “Los triángulos”.
Como sabes, cada triángulo está formado por 3 segmentos de líneas rectas, los cuales, al cruzarse entre sí, forman diferentes ángulos, en este caso se refiere específicamente a los ángulos internos, los cuales son un dato más para que puedas comparar los triángulos entre ellos y puedas deducir si son congruentes, semejantes o de plano no se parecen en nada.
Tienes un triángulo al cual denominarás “ABC”, recuerda la nomenclatura para denominar un triángulo.
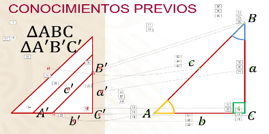
Así nombrarás a sus vértices “A”, “B” y “C”, además nombrarás también los segmentos que lo conforman con letras minúsculas para que las puedas distinguir segmento “a”, “b” y “c”.
Además, tienes también los 3 ángulos internos que forman parte de él, de amarillo tenemos el ángulo que se encuentra en el vértice A.
El ángulo formado por el vértice “B” y el ángulo formado por el vértice “C”. ¿Qué pasaría si copias este triángulo y además lo haces más pequeño?
¿Cómo podrías comparar ambos triángulos? Primero, deberías buscar los vértices correspondientes, por ejemplo, el vértice “A” correspondería ahora con el vértice “A” prima.
Le colocas una comilla y le denominamos “prima”, ya que es el correspondiente con el vértice “A” del triángulo original, esto es una forma de que los identifiques para no confundirte.
Busca ahora el vértice correspondiente a “B”, de esta forma ya tienes dos vértices identificados, lo llamarás “B” prima, por lo tanto, solo queda el vértice “C”.
Ahora tienes un triángulo más pequeño que el original al que denominarás triángulo “A’B’C‘“. Ya has encontrado los 3 vértices, ahora debes encontrar los lados correspondientes entre ambos triángulos.
El lado “a” lo denominarás ahora “a “ prima siguiendo el mismo procedimiento que hiciste con los vértices. El lado “b” con “b’” prima. Y el lado “c” con “c” prima.
Para finalizar, observa que los ángulos del triángulo “ABC” también tienen su ángulo correspondiente en el triángulo “A’B’C’”, observa el primero:
El ángulo formado en el vértice A corresponde con el ángulo formado en el vértice “A” prima y el ángulo del vértice “B“ con el vértice en “B“ prima y por supuesto el ángulo en el vértice “C“ y “C“ prima.
Con estos datos puedes comparar dos triángulos y descubrir si son congruentes, semejantes o de plano no tienen que ver uno con otro.
¿Qué hacemos?
Se enfatiza en los ángulos que los conforman, ya que ellos y la medida proporcional de los lados correspondientes te ayudarán a resolver algunos problemas de la vida diaria, como el que verás a continuación:
Lee el siguiente relato:
Cuando yo era adolescente era un poco inquieto, me gustaba correr y jugar, pero sobre todo probar cosas nuevas, así que un buen día en la casa encontré un bote de pintura en spray (bote de pintura), misma que mi papá había comprado para poder pintar el marco de una ventana, al tomarlo tuve la idea de pintar algo, pero dentro de la casa no encontré nada que se acomodara a mis gustos, quería que fuera algo grande y espectacular, así que salí al patio trasero… y al abrir la puerta… ¡Estaba ahí!, una gran barda pintada de color rojo que me invitaba a utilizar la pintura, no lo dudé y con calma destapé la pintura, la agité y la coloque en dirección a la barda ¡no lo pensé! y escribí una palabra que delataba al autor de los hechos: Jerry, como me decían mis amigos, lo disfruté tanto que lo remarqué hasta que se hicieron más grandes y negras las letras.
En la tarde cuando mi papá regresó de la fábrica donde laboraba recibió una gran sorpresa al asomarse al patio trasero y ver mi nombre pintado en la pared, se molestó tanto que levantó la voz para que yo acudiera a su encuentro, lo primero que me preguntó es que si yo había realizado tal acto de vandalismo en la pared, y al estar de pie frente a esa enorme pared roja y ver mi nombre pintado en ella no pude decir que no, mi padre muy molesto no me dijo nada, solo se metió a la casa y yo me quedé de frente a la pared viendo mi nombre con un gran remordimiento.
Más tarde fui a ver a mi padre y le pedí una disculpa, él me explicó que todos cometemos errores, lo importante era reconocerlos y después tratar de enmendarlos, por lo que decidí pintar la barda con mis propios métodos.
Como buen adolescente no tenía dinero para comprar la pintura que necesitaba para pintar la pared, así que antes que otra cosa me dirigí a la tienda de pinturas y le pregunté al encargado cuánta pintura requería para pintar una barda grande, este me preguntó: ¿Cuántos metros cuadrados mide la barda?
Yo le respondí que era muy alta y larga, sonrió y me dijo: “Ve a donde está la barda, mides el alto y el largo, lo que obtengas lo multiplicas para obtener el área, de esa forma sabes cuantos metros cuadrados de pintura necesitas”, y me mostró un bote de pintura y me dijo: “Esta es la pintura más barata que tengo y un litro te sirve para pintar 10 metros cuadrados, el litro te cuesta 80 pesos.
Regresé corriendo a la casa tratar de medir la barda. El largo lo medí exactamente 12 metros, pero el tratar de medir el alto fue imposible, ya que estaba realmente alta y en la casa no teníamos escalera, fui con mis vecinos y nadie me pudo prestar una, así que fui a recostarme en mi casa a tratar de pensar cómo medir el alto de la barda.
A la mañana siguiente, me asomé a la ventana de mi cuarto, que tiene vista al patio trasero, y observé con curiosidad que el sol brillaba fuertemente sobre la barda y que esta proyectaba una sombra sobre el patio,
Recordé entonces que la maestra de Matemáticas alguna vez nos puso problemas de sombras proyectadas en el piso o algo así, me fui corriendo a buscar mis cuadernos de tercero de secundaria y en los apuntes encontré unos ejercicios que nos puso en donde se podían obtener medidas de lugares inaccesibles solo con la luz del sol.
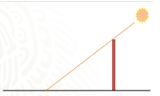
Traté de recordar lo que nos había explicado al ir leyendo los apuntes, pero no encontraba cómo lo había hecho, entonces recordé un problema que tenía un edificio y un poste que reflejaban la luz del sol en el piso y con esos datos podían obtener la altura del edificio sin tener que subirse ni arriesgarse a lastimarse en el intento.
La sombra que proyectaba la barda mediante los rayos del sol, la barda en sí y el suelo; formaban un triángulo, por lo que decidí poner en práctica lo que me había enseñado mi maestra, con mucha emoción fui a ver cómo estaba conformado el triángulo de forma física, llevé un metro para medir las distancias: 9.3 metros era la medida de la sombra del muro sobre el piso, pero algo me faltaba, no podía medir solo el lado de la sombra, algo más faltaba…
¡Algo más me faltaba!, ¡Contra qué lo compararía! Así que busque algo que pudiera mover y ponerlo como el poste del ejemplo del problema de la maestra, busque y busqué hasta que encontré un palo de escoba a la cual le retiré el cepillo, con gran disposición me lo llevé hacia la barda y descubrí que el sol ya había subido más por lo que la medida de la sombra ya no era la misma, me recordé: “El tiempo y el movimiento del planeta siguen su curso, lo tienes que hacer rápido, así que medí primero el palo de la escoba y encontré que exactamente tenía un metro y 19 centímetros, es decir 1.19 metros, pero algo me falta, regresé a mi cuaderno y vi que para que los triángulos fueran semejantes y poder calcular la medida de la barda los ángulos comprendidos entre el lado que es proporcional deben medir lo mismo.
Al medir el ángulo formado por la base del muro el suelo descubrí que medía exactamente 90°, por lo tanto, era un ángulo recto, así que el palo de la escoba debería formar un ángulo congruente con el formado por la pared y el suelo, así que desplacé el palo hacia la sombra que se formaba por la luz del sol sobre la pared haciendo que limitara exactamente con la coronilla superior y trate de formar un ángulo recto entre el palo de escoba y el suelo, como era demasiado trabajo tuve que pedir apoyo a mi hermano para que él lo sostuviera mientras yo tomaba las medidas necesarias.
Sólo me faltaba un ángulo más este ángulo era común a los dos triángulos que ya había formado. ¿Cuáles triángulos? El formado por la barda, el suelo y la sombra del sol y el formado por el palo de escoba, el suelo y la sombra del sol, procedí entonces a medir la base del triángulo mayor y me dio como resultado 8.41 metros después medí la base del triángulo menor y obtuve como resultado 1.75 metros. De esta forma ya había conseguido todas las medidas necesarias, ¿Qué me faltaba?
Realiza los cálculos: Sólo recuerda que el alto del palo de escoba era de 1.19 metros
Es importante obtener la proporcionalidad de los lados correspondientes de cada triángulo, en este caso de sus bases, entonces obtén el cociente de ellos, y divide 8.41 entre 1.75 y obtienes como resultado 4.8, que es el factor constante de proporcionalidad entre los lados correspondientes de ambos triángulos.
Como la altura del muro es el valor que desconoces, lo marcarás como una “x” para poder realizar las operaciones, así que tomas esta incógnita y la divides entre el valor del lado correspondiente del triángulo que es de 1.19 metros.
Y lo igualas a la constante de proporcionalidad que habías encontrado previamente, es decir 4.8. Ahora despejarás la incógnita, en este caso “x” para poder encontrar su valor, como la incógnita está dividiendo a 1.19 y deberás utilizar la operación contraria para poder despejar la “x”, lo que te lleva a multiplicar el segundo miembro de la ecuación por 1.19 y obtienes como resultado 5.71 que es en realidad la altura del muro que estás buscando.
Solo hace falta calcular la cantidad de pintura que va a necesitar y con ello calcular el costo de la travesura.
Si el largo de la barda era de 12 metros y su altura de 5.71, sólo debía multiplicar el largo de la barda por el alto, lo que da como resultado 68.52, pero como se está multiplicando metros por metros, la unidad resultante es metros cuadrados.
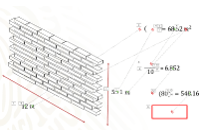
Ahora ya sabes que debe pintar 68.52 metros cuadrados, el vendedor de pinturas le dijo que un litro alcanzaba para 10 metros cuadrados, por lo que se divide 68.52 metros cuadrados entre 10 metros cuadrados que le indicaron para obtener cuántos botes de pintura requiere y ahora sabes que requiere 6.852 botes de pintura.
Pero cada bote cuesta 80 pesos, por lo que se requiere multiplicar para obtener el costo total de la pintura para poder pintar la pared que rayó. Requiere exactamente 548.16 pesos para comprar la pintura. El resultado final del problema es 548.16.
Pero como sabrás, no venden una fracción del bote, entonces se debe comprar completo, por lo tanto, son 7 botes de pintura a 80 pesos, me da en total 560 pesos sólo para la pintura, y eso sin contar el demás material como las brochas.
Todo esto porque no pensó antes de hacer las cosas y rayó una pared que no era suya.
Ahora un resumen de las cosas que realizó para tener claro que fue lo que se utilizó en cada caso.
Para poder medir distancias inaccesibles (como la del muro del problema) puedes utilizar la semejanza de triángulos, estos triángulos deben cumplir con ciertas características para que sean semejantes, en este caso se utilizó el criterio de semejanza ángulo-ángulo, es decir que los ángulos adyacentes a un lado proporcional sean iguales, aunque no es el único criterio ya que existen dos más.
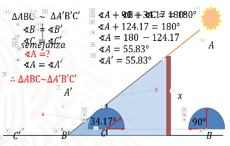
Para eso compara dos triángulos que se obtienen del problema que se planteó, pero, debe quedar claro por qué los dos triángulos son semejantes, de esta forma podrías comprender mejor el corolario que indica que “si dos pares de ángulos correspondientes de dos triángulos son iguales, entonces los triángulos son semejantes”, para eso elimina algunas partes de la imagen que observaste con anterioridad y encontrarás que tienes dos triángulos, los cuales vas a separar para que los puedas contemplar mejor.
Para que puedas identificarlos bien, utilizarás lenguaje matemático, y nombrarás cada vértice de cada triángulo con literales, por ejemplo, del triángulo más grande empezarás por el primer vértice y le pondrás A.
Al segundo vértice le pondrás B y al tercero le pondrás C.
De tal forma que tienes el triángulo ABC y se escribe en lenguaje matemático como triángulo ABC.
De la misma forma, ahora al triángulo más pequeño lo nombrarás según los vértices que corresponden en el triángulo mayor, el vértice A correspondería con el vértice A’ en el triángulo menor. De la misma forma el vértice B con el B’ y por supuesto el vértice C con el C’. Por lo que el triángulo resultante se denominará triángulo A’B’C’.
La idea es demostrar que ambos triángulos son semejantes, lo que se representa matemáticamente con la tilde invertida, pero por ahora la eliminarás hasta comprobar que realmente son semejantes ambos triángulos.
Lo primero que harás es usar un transportador para medir el ángulo en B y observa que mide exactamente 90°. Mide ahora el ángulo correspondiente en B, es decir B’ y observa que también mide 90°, por lo tanto, el ángulo en B es igual al ángulo en B’.
Ahora mide el ángulo en C, coloca tu transportador y mide exactamente 34.17°.
Con el mismo transportador mide ahora el ángulo en C’ y observa que mide 34.17°, por lo tanto, los dos ángulos son iguales.
Ya comparaste dos ángulos correspondientes de cada triángulo y observaste que miden lo mismo, pero falta el tercer ángulo, es decir, el que se encuentra en el vértice A y en A’ pero ya no lo medirás, ahora utilizarás un teorema que ya es conocido, y es aquel que dice: “La suma de los ángulos interiores de un triángulo es igual a 180°”.
Si sumas el ángulo en A más el ángulo en B + el ángulo en C debe dar en total 180°.
Ahora reemplaza el valor del ángulo en B por el que ya tenías que es 90° y el del ángulo en C por 34.17°. Suma los valores y obtienes 124.17°. Despeja el ángulo en “A” restándole a ambos miembros de la ecuación 124.17 y obtienes como resultado la medida del ángulo en A el cual tiene un valor de 55.83°, en el caso del triángulo A’B’C’ los valores de los ángulos son los mismos, por lo que el valor del ángulo en A’ es igual al valor del ángulo en A. Por lo tanto, matemáticamente has encontrado que en ambos triángulos los ángulos correspondientes miden lo mismo, por lo que deduces que son semejantes.
Probablemente pensaste que la geometría es difícil, sin embargo, está presente en el día a día, todos utilizamos algo que se llama razonamiento deductivo, el cual permite inferir respuestas desde observaciones comunes, así como cuando ves que el cielo se nubla, podrías pensar que hay una probabilidad que llueva, de la misma manera a lo largo de la humanidad diferentes pensadores y filósofos han ido acrecentando el conocimiento matemático. Realiza la siguiente lectura, es de tu libro de matemáticas de segundo grado para que conozcas un ejemplo:
“Eratóstenes fue un matemático, astrónomo, geógrafo y poeta griego. Fue llamado a Egipto, en el año 236 a. C., para que se hiciera cargo de la biblioteca de Alejandría, donde aprendió que Siena (hoy Asuán, en Egipto) está situada prácticamente sobre el trópico de Cáncer, y por esto, el día del solsticio de verano, a mediodía, los objetos no proyectan sombra.
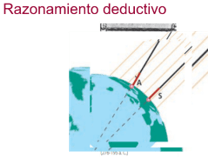
En Alejandría, en el solsticio de verano, Eratóstenes enterró una vara en el suelo y notó que, a pesar de ser mediodía, esta proyectaba sombra. Determinó, mediante un instrumento parecido al reloj solar, que el ángulo que se formaba entre la vara y los rayos del sol era de un cincuentavo de trescientos sesenta grados. Pensó que como el Sol se encuentra tan alejado de la Tierra sus rayos podían suponerse paralelos entre sí.”
“Eratóstenes mandó medir la distancia entre Siena (representado por una “S” y Alejandría (representada por una “A”), pero es probable que ya conociera ese dato. La distancia que utilizó para sus cálculos fue de 5 000 estadios. Esta distancia es la longitud del arco de circunferencia comprendido entre A y S.
Conociendo la medida del ángulo ACS y la longitud del arco AS, Eratóstenes pudo calcular la longitud de la circunferencia terrestre”
Sólo con la deducción matemática Eratóstenes pudo medir la distancia de la circunferencia de la tierra apoyado en la observación de fenómenos naturales que existían a su alrededor, en este caso de los rayos del sol, como lo hiciste en esta lección.
Te sugerimos que seas más observador con lo que ocurre a tu alrededor, analízalo y observa hasta dónde te conduce, te maravillarás de lo que puedes descubrir.
Para finalizar anota en tu cuaderno el criterio de semejanza de triángulos que trabajaste, lo conoces como el criterio ángulo-ángulo; en donde encuentras que: “Si dos pares de ángulos correspondientes de dos triángulos son iguales, entonces los triángulos son semejantes”. Si recuerdas este corolario te podrás ahorrar muchos cálculos en un futuro.

El reto de hoy:
Te recomendamos buscar en tu libro de texto de Matemáticas de tercer grado, problemas de semejanza de triángulos que utilicen el criterio ángulo-ángulo, los podrás encontrar en el Bloque I.
¡Buen trabajo!
Gracias por tu esfuerzo.