Yo también quiero una beca
Yo también quiero una beca
Aprendizaje esperado: calcula la media (promedio). Analiza su pertinencia respecto a la moda como dato representativo en situaciones diversas.
Énfasis: resuelve problemas que implican obtener la media aritmética (promedio), como un valor representativo.
¿Qué vamos a aprender?
Aprenderás a resolver problemas que implican obtener la media aritmética (promedio) como un valor representativo.
¿Qué hacemos?
En la sesión de hoy resolveremos problemas que implican obtener la media aritmética a la que todos conocemos comúnmente como promedio.
Comenzaremos resolviendo los problemas del desafío número 97 “Vamos por una beca” que se encuentra en la página 189 de tu libro de Desafíos Matemáticos.
https://libros.conaliteg.gob.mx/20/P5DMA.htm#page/189
La consigna dice:
En pareja resuelvan los siguientes problemas.
- Ernesto, Joaquín, Sara y Elisa están concursando por una beca para estudiar. Quien obtenga mínimo 8.2 de promedio obtendrá la beca. En la siguiente tabla se muestran las calificaciones que han obtenido en los cuatro bimestres.
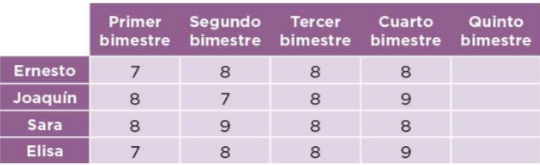
La pregunta con el inciso a) dice: Hasta el cuarto bimestre, ¿Quién tiene posibilidades de obtener la beca?
Vamos a calcular los promedios y resolvamos estos problemas.
¿Ya tienes alguna idea, de cómo resolverlo?
Lo primero que debemos hacer es conocer el promedio de cada uno de los alumnos.
¿Y cómo podemos calcularlo?
Debemos sumar las calificaciones de cada alumno y dividirlo entre 4 porque son 4 bimestres.
Empiezo con el de Ernesto, sumamos 7 más 8 más 8 más 8 y esto es igual a 31. Ahora dividimos 31 entre 4 y esto es igual a 7.75 por lo tanto, el promedio de Ernesto es 7.75
Ahora vamos a calcular el promedio de Joaquín. Sumamos 8 más 7 más 8 más 9 y esto es igual a 32. Ahora dividimos 32 entre 4 y esto es igual a 8.0 por lo tanto, el promedio de Joaquín es 8.0
Vamos a calcular el promedio de Sara. Sumamos 8 más 9 más 8 más 8 y esto es igual a 33. Ahora dividimos 33 entre 4 y esto es igual a 8.25
Para el promedio de Elisa, sumamos 7 más 8 más 8 más 9 y esto es igual a 32. Ahora dividimos 32 entre 4 y esto es igual a 8.0 por lo tanto, el promedio de Elisa es 8.0
Ahora contestemos. ¿Quién tiene posibilidades de obtener la beca? Si el promedio que se requiere es 8.2 de acuerdo con los promedios obtenidos hasta este momento, Sara sería la única con posibilidades de obtener la beca.
¿Por qué?
Porque su promedio es de 8.25 que es un poco más que 8.2
Continuemos con la siguiente pregunta dice así:
b) ¿Qué calificación como mínimo necesita obtener cada uno en el quinto bimestre para que le den la beca?
¿De qué manera, podríamos dar respuesta a esta pregunta?
Podríamos experimentar colocando una calificación probable en el quinto bimestre para cada alumno, de tal manera que alcancen el promedio de 8.2 requerido para la beca.
Empecemos con Ernesto. ¿Qué calificación deberá obtener en el quinto bimestre?
Vamos a probar con el número 9 de calificación en el quinto bimestre. Ahora, sumamos 7 más 8 más 8 más 8 más 9 y esto es igual a 40. Ahora dividimos 40 entre 5 porque son 5 bimestres y esto es igual a 8.0
¡Qué triste! No le alcanza.
Podemos intentar con 10 en el quinto bimestre, ahora, sumamos 7 más 8 más 8 más 8 más 10 y esto es igual a 41. Ahora dividimos 41 entre 5 porque son 5 bimestres y esto es igual a 8.2
Si Ernesto pone mucho empeño en la escuela seguro obtendrá 10 y de esta manera alcanzará el promedio de 8.2 que requiere para obtener la beca.
Entonces escribe que la calificación mínima que debe obtener Ernesto en el quinto bimestre es 10
La calificación que debe de obtener Joaquín en el quinto bimestre. Como ya sabemos su promedio de los 4 bimestres fue 8 entonces si obtiene en el último bimestre 8 el promedio no se modificará porque 8 más 8 es igual a 16 y 16 entre 2 es igual a 8
Pero, con 8.0 no le alcanza el promedio para obtener la beca, porque se necesita tener 8.2 de promedio.
Por eso intentaremos con 9 de calificación en el quinto bimestre. Sumamos 8 más 7 más 8 más 9 más 9 y esto es igual a 41. Ahora dividimos 41 entre 5 y esto es igual a 8.2
Por lo tanto, Joaquín necesita sacar 9 en el quinto bimestre para obtener promedio de 8.2 y así podrá alcanzar el promedio para obtener la beca.
Escribe 9 junto al nombre de Joaquín.
Vamos a calcular la calificación mínima que debe obtener Sara en el quinto bimestre.
Como ya vimos, Sara tiene un promedio de 8.25 hasta el cuarto bimestre. Si obtiene 8 en el quinto bimestre, sumamos 8 más 9 más 8 más 8 más 8 y esto es igual a 41. Ahora dividimos 41 entre 5 y esto es igual a 8.2
Por lo tanto, la mínima calificación que Sara debe obtener en el quinto bimestre para alcanzar la beca es de 8
Escribe 8 junto al nombre de Sara.
Pero podría también obtener 9 o 10 para que tenga un promedio más alto que 8.2
Recuerda que en el libro nos están pidiendo la calificación mínima que deben obtener en el quinto bimestre, para obtener el promedio de 8.2
Por eso le debemos poner a Sara 8 de calificación.
Continuamos con las calificaciones de Elisa.
Como ya sabemos el promedio de Elisa de los 4 bimestres fue 8 entonces si obtiene en el último bimestre 8 el promedio no se modificará porque 8 más 8 es igual a 16 y 16 entre 2 es igual a 8
Pero, con 8.0 no le alcanza el promedio para obtener la beca, porque se necesita tener 8.2 de promedio.
Por eso lo intentaremos con 9 sumamos 7 más 8 más 8 más 9 más 9 y esto es igual a 41 ahora dividimos 41 entre 5 y esto es igual a 8.2
Por lo tanto, el promedio final de Elisa sería 8.2 pero la calificación mínima que debe obtener en el quinto bimestre es 9
Escribe 9 junto al nombre de Elisa.
Vamos por el siguiente problema:
El problema 2 de tu libro de desafíos dice: que 10 estudiantes pesaron un objeto con el mismo instrumento y cada uno obtuvo un peso determinado que tenemos anotado abajo.
En el inciso a) nos preguntan cuál fue el peso mayor. ¿Cuál sería la respuesta?
Antes de comenzar a responder, podríamos ordenar los valores del menor al mayor o al revés, así nos será más fácil analizar esta información.
Del menor al mayor, 59, 59, 60, 60, 61, 61, 62, 62, 62, 64
Así ya tenemos la respuesta del inciso a) el mayor peso obtenido fue de 64 gramos.
También el inciso b) ya es fácil de responder, el peso menor es 59 gramos.
Ahora, ¿Qué podemos hacer para responder el inciso c)?
c) ¿Cuál sería la mejor estimación del peso real del objeto?
Podemos sacar el promedio de lo que todos obtuvieron y eso nos daría la mejor estimación del peso del objeto, que sería:
59 + 59 + 60 + 60 + 61 + 61 + 62 + 62 + 62 + 64 = 610
La suma de los 10 valores que obtuvieron nos da 610 luego hay que dividirlo entre 10 y nos da 61. Así que sería 61 gramos la mejor estimación del peso de ese objeto.
En la sesión de hoy aprendimos a resolver problemas que implican obtener la media aritmética o promedio. Seguramente tú obtuviste las mismas respuestas que nosotros, pero si aún tienen dudas, acude a tu maestra o maestro, para que te ayude a comprender mejor esto de los promedios.
¡Buen trabajo!
Gracias por tu esfuerzo.
Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas
