¿Y si necesitamos agrupar?
¿Y si necesitamos agrupar?
Aprendizaje esperado: desarrolla y ejercita un algoritmo para la división entre un dígito. Usa el repertorio multiplicativo para resolver divisiones (cuántas veces está contenido el divisor en el dividendo).
Énfasis: inicia la construcción de un algoritmo para resolver divisiones entre un dígito.
¿Qué vamos a aprender?
Desarrollarás y ejercitarás un algoritmo para la división entre un dígito. Usarás el repertorio multiplicativo para resolver divisiones, es decir, cuántas veces está contenido el divisor en el dividendo.
¿Qué hacemos?
Aprenderás como es el trabajo en equipo. Lee con atención.
María comenta que su primo se dedica a dar cursos y explica brevemente sobre los cursos.
La mayoría tienen que ver con el trabajo en equipo, la colaboración y temas relacionados.
Son temas muy interesantes e importantes, porque cada vez es más difícil que la gente quiera unirse para un fin común, para trabajar en equipo.
Por lo mismo siempre trabaja las actividades en equipos, para que además de aprender, puedan ponerlo en práctica.
Hasta aquí todo parece muy bueno, porque también en las escuelas el trabajo en equipo rinde buenos frutos y nos ayuda a desarrollar otras habilidades y hábitos independientes a los temas que se están trabajando, sin embargo, aún no encuentro la coincidencia con el título de la sesión.
¿Y si necesitamos agrupar? suena a lo que hace el primo de María. Él siempre divide el total de asistentes a sus cursos en equipos según el tema que va a desarrollar.
Ahora ya entendiste la coincidencia y, en efecto, hoy vamos a separar, agrupar y dividir.
Una vez que logremos distinguir lo que debemos hacer y cómo es mejor hacerlo, verás que es muy sencillo.
¿Eso significa que puedes ayudar a formar los equipos que le pidió su primo a María?
Sirve que con esos vas practicando.
Estas son las dos tarjetas que le dio su primo de María para ayudarle.
¿Qué te parece si comenzamos con la de letras rojas?

Es importante que practiques la formulación de problemas. ¿Puedes, con esta información, formularás uno?
Hay datos y además hay una interrogante, así que si se puede hacer.
El primo de María se llama: Sergio.

Exactamente eso es lo que queremos saber para ayudar a su primo Sergio.
Tendrás que agrupar a las y los 30 asistentes de 4 en 4 ¿De qué manera lo puedes resolver?
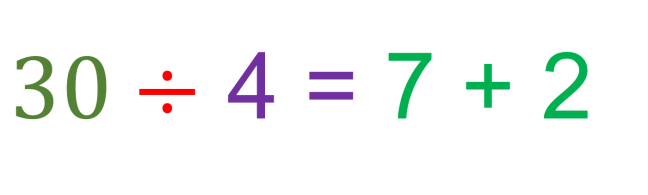
Puedes hacerlo mentalmente, sólo recordemos que para poder dividir es muy importante conocer y comprender las tablas de multiplicar.
Para resolver esta división debe encontrar un número que multiplicado por 4 sea 28 o que se acerque mucho, pero que te pase.
¿Qué número es ese?
4 x 1 = 4, 4 x 2 = 8, 4 x 3 = 12, 4 x 4 = 16, 4 x 5 = 20, 4 x 6 = 24, 4 x 7 = 28, es el 7, porque 4 por 7 son 28 y faltan dos para llegar a 30
¿Cuál sería entonces la respuesta a la pregunta?
La pregunta decía, ¿Cuántos equipos se formarán? Y su respuesta es 7 equipos.
En efecto, se van a formar 7 equipos, pero, ¿Qué hará con las dos personas que hay de más? pues son 30 los asistentes al curso.
Pues como dijo que no debían ser equipos con menos de 4 personas, entonces las dos personas restantes las podemos integrar una a cada equipo; así serán 7 equipos, pero habrá 5 equipos con 4 personas y 2 equipos con 5 personas, porque estamos incluyendo a las dos personas que hay de más.
Esa es la respuesta correcta, recuerda que siempre debe considerar tu total, que en este caso era de 30 personas inscrita al curso, siguiente tarjeta, la de letras moradas.

¿Puedes convertirlo en un problema?

. En este caso debes dividir 50÷9
9 = 6
Nuevamente busca un número que multiplicado por 9 sea 54 o que se acerque mucho al 54 sin pasarse. Voy a empezar desde 9 x 5 = 45, 9 x 6 = 54 es el 6
En cada equipo habrá 6 personas, terminamos de ayudar al primo de María y repasamos también algunos de nuestros temas de clase pues teníamos un conjunto, en este caso de personas, y las dividimos o agrupamos en conjuntos más pequeños.
¿Crees que existan otras formas de resolver estos problemas que no sea con cálculo mental?
Podríamos realizar una operación escrita.
El cálculo mental es una gran herramienta y debemos intentar usarla lo más que podamos para mejorar nuestras habilidades, pero hay situaciones en las que es muy complicado usarlo y es preferible hacer la operación escrita, por lo que es muy importante comprender el problema para decidir lo que vamos a hacer.
Para continuar con este tipo de situaciones necesitas abrir tú libro de desafíos matemáticos tercer grado en las páginas 156 y 157

https://libros.conaliteg.gob.mx/20/P3DMA.htm?#page/156
¿Lee la consigna?

¿Qué se te ocurre que podemos hacer para contestar la pregunta?
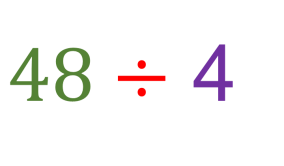
Pues dividir las 48 personas que llegaron en grupos de 4, es decir, podemos dividir 4, pero ¿Cómo resolvemos esa división?
- Observa, podemos hacerla por partes. Sabemos que si multiplicamos 4 por 10 son 40 y luego podemos dividir los 8 que hay de más entre 4 pero se te va a explicar cómo escribir la división con la galera.
¿Te refieres a poner la que llamamos “casita” para resolver la división? Así es.
Quizás se te haga más fácil acordarme de la “casita” de la división, pero ya sabes que su nombre es galera.
Perfecto. Anota en tu cuaderno la división 4 pero con la galera.
Dibuja la galera, luego adentro ponemos el 48 porque es el número que vamos a repartir y afuera el 4, porque es la cantidad de personas que debe ir en cada grupo.
Exacto el 48 es el número que se va a repartir así que va dentro de la galera, la cantidad entre la que se reparte va afuera, en el divisor y ahora mira, haremos la división por partes dijimos que 10 por 4 son 40 anotemos aquí el 40 y lo restamos a 48 son 8 con esos 8 todavía podemos hacer 2 grupos más, entonces anotamos aquí más 2 por 4 son 8 y los restamos a los 8 que teníamos, ya no sobró nada.
Mientras anota el nombre de cada parte de la división.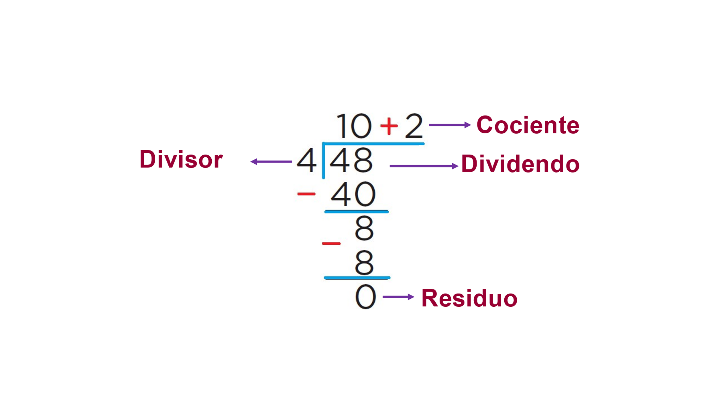
- Leerás un problema o situación y el número que repartes va anotado adentro de la casita, perdón de la galera.
Sí y afuera va el divisor, que es el número que está dividiendo al de número de adentro; es decir, el número que me indica entre cuántos se va a dividir el número que está adentro.
Adentro dividendo, afuera divisor. Damos por terminada la operación cuando el residuo, es decir, lo que sobra, es menor que el dividendo.
Una vez resuelta, encontramos que esto que está acá arriba se llama cociente y es una parte del resultado de la división y acá abajo encontramos el residuo, es decir los elementos que no alcanzaron a formar un nuevo grupo.
Entonces, adentro dividendo, afuera divisor, arriba cociente, abajo residuo.
Ahora cabe hacer la aclaración de que una división escrita con la galera, se lees al revés de cómo estamos acostumbrados, es decir, siempre leemos de izquierda a derecha, pero sería un error leerla así porque diríamos 4 entre 48 lo cual es falso ya que no estamos dividiendo 4 entre 48, sino al revés; entonces leemos de derecha a izquierda, es decir, 48 entre 4
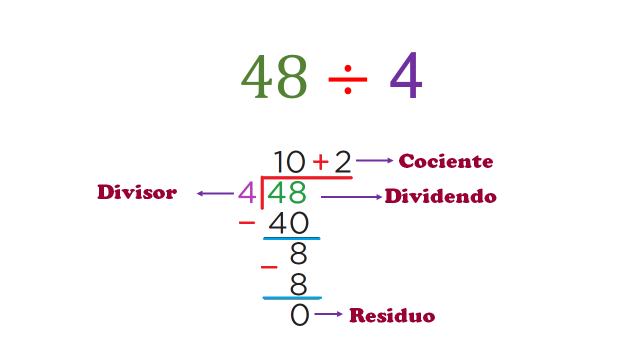
Si yo encuentro una división así 4 la puedo leer normal, cuarenta y ocho entre 4 pero al momento de acomodar en la casita, digo, de la galera, se lee al revés.
Entendido y explicado.
Entonces la respuesta a nuestro primer ejercicio sería 10 + 2
La respuesta sería: se formaron 12 brigadas. ¿Cómo podrías explicar la respuesta?
Son 12 brigadas, porque al multiplicar 4 trabajadores por 12 brigadas nos da como resultado 48 trabajadores.
Es correcto.
Ahora vamos con el ejercicio 2 a otra comunidad llegaron 53 trabajadores. ¿Cuántas brigadas de 4 trabajadores se podrán formar? Expliquen su respuesta.
Ahora dividiríamos 53 4
Otra vez el número que nos ayuda porque podemos multiplicar fácilmente por él es el 10
Lo colocamos como cociente y decimos 4 x 10 = 40 y hacemos la resta, nos sobran 13
Realiza la operación tomando en cuenta la imagen de referencia.
Con el 13 aún puedo hacer 3 grupos más, porque 4 x 3 = 12
En el cociente escribimos + 3 y abajo restamos 13 – 12 = 1
Eso significa que se formaron 13 brigadas, porque 4 x 13 = 52 y sobra un trabajador que no alcanza a formar una nueva brigada.
En este caso esa sería la respuesta ya que la pregunta es muy específica, ¿Cuántas brigadas de 4 trabajadores se podrán formar?
¿Hay casos donde podríamos tener otra respuesta?
Por ejemplo, si la pregunta no especificara diciendo “4 trabajadores”, tendríamos que incorporar al trabajador restante en alguna brigada, pero como aquí nos lo específica, no es necesario.
Entonces, si la pregunta no fuera así de específica, la respuesta puede ser: 12 brigadas con 4 trabajadores y 1 brigada con 5 trabajadores y lo explicaría diciendo que esto es porque 4 x 13 es 52 y sobra 1 trabajador que no alcanzó a formar otra brigada de 4 trabajadores y se puede incorporar a una brigada.
¿Cómo vas?
Te das cuenta que estas recordando temas vistos y comprendiendo cosas nuevas.
Pasa al ejercicio 3 que tiene nuevos retos para todos y todas.

Lee con mucha atención el ejercicio:
Lo que debemos hacer aquí son grupos de 3 con las 74 personas que asistirán, es decir 74 3 ¿Podrías hacer ahora tú la operación?
Dibuja la galera, pon el número que vas a repartir adentro que es el 74 y el 3 afuera, porque corresponde al número de personas que habrá en cada habitación y comenzamos a hacer la división.
¿Podemos hacer 10 conjuntos de 3?
Sí 3 x 10 es 30
Pero, en este caso falta mucho todavía para el 74 así que usaremos múltiplos de 10 para encontrar un número que se acerque más. ¿Se pueden hacer 20 equipos de 3?
Multiplica 3 x 2 = 6 y le agrega el 0 = 60 anota el 20 aquí y resta 60 a 74. Ve realizando la operación tomando en cuenta las operaciones de referencia.
74 – 60 = 14
Y con los 14 que restan se podrían hacer 4 grupos más porque 3 x 4 = 12 y sobran 2
¿Cuál sería entonces la respuesta?
24 habitaciones no, perdón, 25
¿Por qué 25, si el resultado fue 24?
Porque preguntan cuántas habitaciones necesitamos para alojar a todas las personas, eso quiere decir que se usarán 24 habitaciones para tres personas y en la última sólo habrá 2 personas, porque no podemos dejar sin habitación a esas personas que sobraron.
Mejor explicado imposible, jajaja. Exacto, hay casos donde repartimos frutas, por ejemplo, y podemos fraccionar las que sobren para repartir en partes iguales o dejarla sin repartir, pero en este caso no podemos dejar a dos personas sin habitación.

Entonces la respuesta es: Se necesitan 25 habitaciones para alojar a todas las personas.
Con la misma información resolveremos el inciso b

Como seguimos hablando de las mismas 74 personas, ahora dividiremos 74 7
Escribe de nuevo, dentro de la galera el 74 afuera el 3 y comenzamos. Ve registrando tus operaciones.
Usaremos nuevamente el 10 que nos facilita mucho las operaciones.
- x 10 = 70 así que en el cociente pondré el 10 y acá restaré 70 y me sobran 4
¿Cuántos equipos se pueden formar entonces?

Se podrán formar 10 equipos de 7 personas y 1 de 4 personas.
Así puedes expresar la respuesta ya que en esta ocasión no nos pregunta específicamente cuántos equipos de 7 personas se pueden formar.
¡Vamos por el último inciso de esta actividad!

Ahora dividimos 74 4
Traza la galera anotando adentro el dividendo que es 74 y afuera el divisor que es 4 y a resolver. Realiza las operaciones correspondientes:
4 x 10 = 40
Pon el 10 como cociente y abajo resto 74 – 40 = 34
4 x 5 = 20, 4 x 6 = 24, 4 x 7 = 28, 4 x 8 = 32, pondríamos + 8 como cociente también.
Aquí pon el + 8 y resto 34 – 32 = 2
Siguiendo la lógica que hemos usado, necesitamos 19 mesas para que todos y todas tengan lugar en una mesa.

Se necesitan 19 mesas. Ya que 18 estarán utilizadas en toda su capacidad, es decir con 4 personas y 1 sólo estará ocupada por dos personas.
Esta es una forma de resolver divisiones y esperamos te haya gustado mucho porque es bastante sencilla.
Es muy importante tener alternativas para llegar a los resultados correctos.
También debes de considerar construir y aplicar diferentes caminos que te permitan dar solución a situaciones, no debes perder de vista que también hay que explorar nuevas formas de llegar a los mismos resultados y usar los que se nos hagan más fáciles.
Y una cosa más, el dominar las tablas de multiplicar también te facilitará la resolución de problemas así que hay mucho que practicar.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas

