Y ahora, ¿cómo va? Sucesiones simples de figuras

Y ahora, ¿cómo va?

Sucesiones simples de figuras

Aprendizaje esperado: identificación de la regularidad en sucesiones compuestas con progresión aritmética, para encontrar términos faltantes o averiguar si un término pertenece o no a la sucesión.

Énfasis: identificar la regularidad en una sucesión compuesta formada por figuras. (1/2)

¿Qué vamos a aprender?

Aprenderás a identificar la regularidad en una sucesión formada por figuras.

¿Alguna vez has visto muñecas como las que se muestran en la siguiente imagen?

Estas muñecas se llaman Matryoshkas y son una artesanía que tiene la particularidad de que se encuentran huecas y en su interior albergan una nueva muñeca, y esta a su vez a otra, en un número variable que puede ir desde cinco hasta el número que se desee, aunque por la dificultad de tamaño, es raro que pasen de veinte.

Parece tal vez difícil querer ordenarlas, sobre todo porque son muchas. Sin embargo, si se pone atención en el tamaño de las piezas y se compara una figura con otra, lo que tienen igual y diferente, puedas encontrar la forma de ordenarlas más fácilmente.

En las Matemáticas se estudia algo parecido, se conoce con el nombre de sucesiones, progresiones o series y justamente ese es el tema que verás hoy.

¿Recuerdas que en el Jardín de niños en algunas ocasiones clasificaste u ordenaste piezas por su color o tamaño y las colocabas en un orden determinado?, pues eso es un ejemplo de una sucesión, progresión o serie.

Para empezar el trabajo del día de hoy, lee con atención lo que es una sucesión:

Una sucesión es un conjunto ordenado de elementos (números, letras, figuras, etc.) que responden a una regla de diseño o construcción. A los elementos de la sucesión se les llaman términos. Las sucesiones se construyen siguiendo una regla.

El día de hoy verás sucesiones de figuras, donde hay una regularidad, características o patrón de construcción de la sucesión que permite determinar todas las figuras que forman parte de la progresión; empezando por la que ocupa el primer lugar de la sucesión, luego la que ocupa el segundo, luego la que ocupa el tercero y así sucesivamente.

Se llama figura 1 o primer término a la que ocupa el primer lugar en la sucesión, figura 2 o segundo término a la que ocupa el segundo lugar, figura 3 o tercer término a la que ocupa el tercer lugar y así sucesivamente.

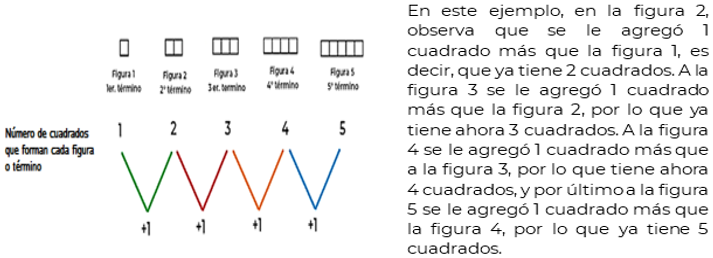
Observa el siguiente ejemplo con figuras construidas a partir de un cuadrado.

Analiza cómo se construyeron los términos de la sucesión, los cuales por cierto utilizan los números ordinales: 1°, 2°, 3°, 4°, 5°, 6°, etc., para indicar precisamente el lugar que ocupan en la serie:

El primer término, que representa la figura 1; está compuesto por un cuadrado; el segundo término, que representa la figura 2, está compuesto por 2 cuadrados; el tercer término, que es la figura 3; está compuesto por 3 cuadrados; el cuarto término que representa la figura 4, está compuesto por 4 cuadrados y el 5° y último término que lo representa la figura 5, está compuesto por 5 cuadrados.

Como puedes observar en la imagen, a cada término se le van agregando más cuadrados de manera que la figura incremente el número de ellos, y esta cantidad se obtiene al ir sumando una cantidad que puede ser en algunos casos constante, o sea la misma, al término anterior o figura anterior. En este caso, se agrega un cuadrado a cada término.

Esto se puede representar también numéricamente como una serie de números:

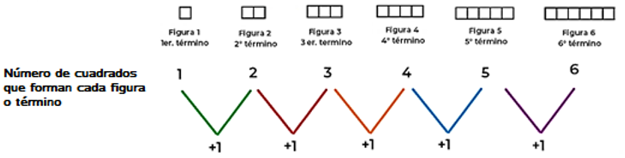
Seguramente ya observaste lo que se tiene que hacer para dibujar la sexta figura: debes aumentar en uno el número de cuadrados con relación a lo que se aumentó en la figura anterior.

Así que, ¿cuántos cuadrados se deben dibujar al quinto término, para obtener el sexto? La respuesta es: uno más

Este enunciado, en el que se indica lo que se debe hacer para construir cada uno de los términos de la sucesión, es la regla de construcción o diseño. Puedes escribirla entre comillas, siempre iniciando con una mayúscula, si quieres también puedes escribirla con un color distinto, subrayarla o resaltarla con marca texto, etc., de manera que la identifiques en tus notas con más facilidad y recordarla si vas a seguir obteniendo nuevos términos.

Ahora observa la siguiente figura:

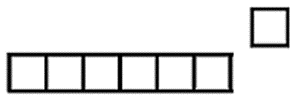
¿Cuántos cuadrados tiene?

¿Podría esta figura, ser el 7° término de la serie que has venido analizando?

Como ves, tiene 7 cuadrados y la figura anterior tenía 6 y, como se va agregando un cuadrado a cada término, puede ser que sí sea el séptimo. Sin embargo, observa con mucha atención si tiene algo distinto esta figura con relación a las anteriores.

Seguramente te habrás fijado que el séptimo cuadrado a la izquierda no se encuentra alineado al resto, esto hace que la figura no respete la posición de los cuadrados que se van agregando y por lo tanto no podría esta figura ser el 7° término de la sucesión.

Para que eso sea posible debe dibujarse unido al lado del último cuadrado del término anterior:

Es muy importante que además de identificar la regla de construcción, tengas muy claro la posición en la que debes agregar las nuevas figuras que formarán el término que vas crear; de manera que, considerando lo anterior se puede complementar la redacción de la regla de construcción o diseño, por ejemplo, de la siguiente manera:

Seguramente ya tienes una redacción propia para esta regla. La progresión quedaría dibujada correctamente hasta el séptimo término de la siguiente manera:

Esta actividad que acabas de realizar, te permitirá continuar con el trabajo de la sesión del día de hoy.

Si tienes libros en casa o cuentas con Internet, explóralos para saber más.

¿Qué hacemos?

Analiza la siguiente sucesión de figuras:

Asigna un número a cada figura según corresponda.

¿Cuál sería la figura 1 o primer término?… la que tiene un triángulo.
¿Cuál sería la figura 2 o segundo término?… la que tiene 4 triángulos.
¿Cuál sería la figura 3 o tercer término?… la que tiene 7 triángulos.
El cuarto término, ¿cuántos triángulos debe tener y cómo deben dibujarse?

Como te puedes dar cuenta, asignar el lugar a cada término de la sucesión fue relativamente fácil, ahora ¿Ya descubriste qué debes hacer para dibujar los términos que siguen?

Si aún no lo sabes, cuenta cuántos triángulos tiene el primer término, cuántos el segundo término y cuántos el tercer término.

Como seguramente ya te habrás dado cuenta debes incrementar el número de triángulos a medida que vas creando términos de la sucesión hacia la izquierda.

¿Cuántos triángulos debes agregar cada vez? Si calculaste correctamente, son tres triángulos cada vez, pero además es importante que tomes en cuenta la variación en la posición de los triángulos que se van a dibujar.

Con esa información ya puedes redactar una regla de construcción de la serie. Además, si te fijas es una serie creciente, porque cada nuevo término tiene más elementos que el anterior.

Una posible redacción de la regla de construcción o diseño puede ser la siguiente:

Tú puedes realizar una redacción propia de la regla de construcción

Si quieres determinar el cuarto término o figura, ¿cuántos triángulos deberá tener?, ¿cómo sería su representación? Dibújala.

Seguramente dibujaste la figura 4, con 10 triángulos y de la siguiente manera.

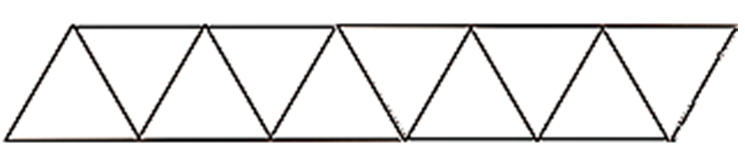
Y se puede observar que el patrón de crecimiento de los términos, indica que los triángulos que se agregan, se dibujan invirtiendo alternadamente la posición de su base.

La serie desarrollada hasta el 4° término se vería así:

Analiza la siguiente sucesión para seguir practicando: En la siguiente sucesión ¿Cuál será su regularidad?

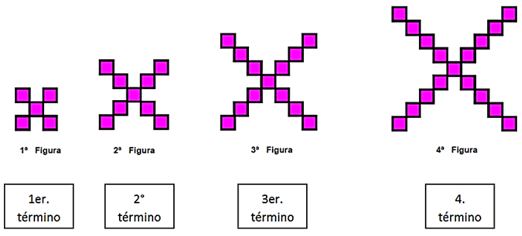
Seguramente contar muchos cuadrados te confunde un poco, qué tal si elaboras algún registro que te ayude a tener presente la información que vas encontrando, por ejemplo, al contar los cuadrados anotas cuantos tiene cada figura, de la siguiente forma:

Analiza: la figura 1 tiene 5 cuadrados, la figura 2 tiene 9 cuadrados, la figura 3 tiene 13 cuadrados y la figura 4 tiene 17 cuadrados. Por lo que la regla de construcción, regularidad o patrón de diseño, puede tener la siguiente redacción:

Analiza la siguiente sucesión:

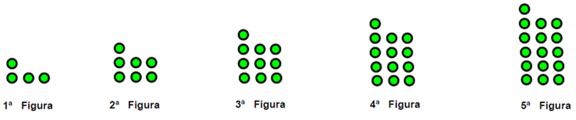
Al examinar las figuras, puedes observar que: la figura 1, tiene 4 círculos; la figura 2 tiene 7 círculos; la figura 3 tiene 10 círculos; la figura 4 tiene 13 círculos y la figura 5 tiene 16 círculos. Por lo que la regularidad o patrón de diseño, puede expresarse de la siguiente manera:

Examina una sucesión más. Obsérvala a continuación.

Como puedes ver, la figura 1 tiene 1 cuadrado; la figura 2 tiene 3 cuadrados; la figura 3 tiene 6 cuadrados y la figura 4 tiene 10 cuadrados. Por lo que la regularidad o patrón de diseño, es que:

Reflexiona sobre la siguiente situación:

¿Qué pasa si en una sucesión faltaran una o varias figuras? ¿Cómo puedes saber cuántos elementos las integran?

Para responder a estas preguntas, analiza el siguiente ejemplo:

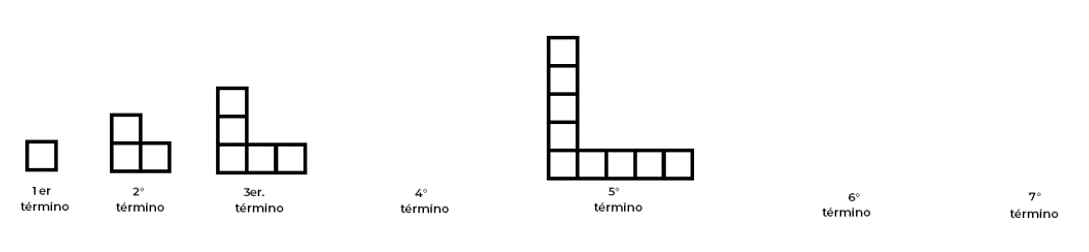
Como has hecho en los ejemplos anteriores, primero identifica la regularidad o el patrón de crecimiento: en la figura 1 hay un cuadrado, la figura 2 tiene 3 cuadrados, es decir dos más que la anterior; la figura 3, tiene 5 cuadrados, también dos más que la anterior. Entonces por lo que concluimos que la regularidad de diseño o construcción es:

Ahora ¿Cuántos cuadrados tendrá la figura 4?

Si la figura 3, tiene 5 cuadrados y si la regularidad va de dos en dos, se le agregarían dos cuadrados más; por lo que la figura 4 tendrá, 7 cuadrados.

Dibujada quedaría más o menos así:

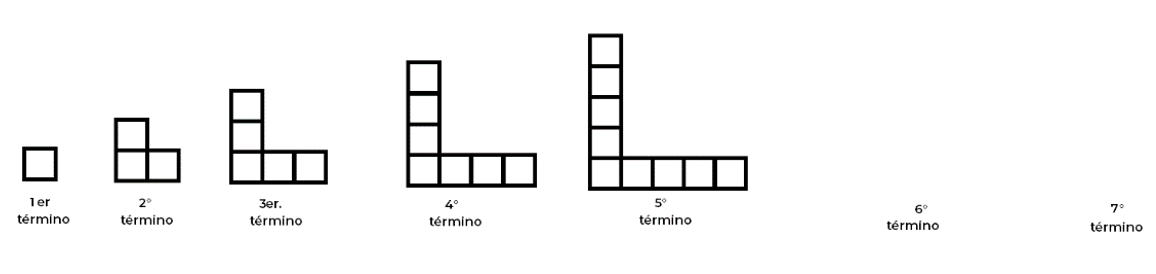
La figura 5, como puedes ver, tiene 9 cuadrados, entonces ¿Cuántos cuadrados tendrán las figuras 6 y 7?

Si la figura 5, tiene 9 cuadrados y le sumo 2, la figura 6 tendrá 11 cuadrados, y si a la figura 6 le sumo dos más, la figura 7 tendrá 13 cuadrados.

La sucesión, hasta la figura 7, quedaría de la siguiente manera:

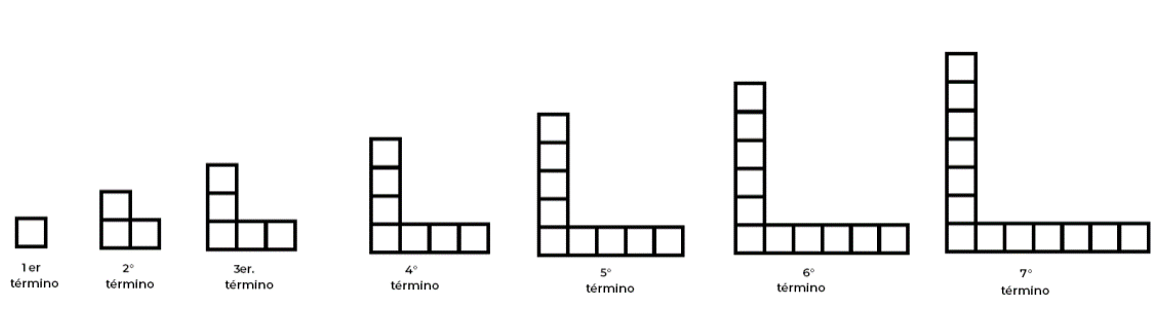
Analiza la siguiente sucesión de figuras:

¿Cuántos círculos tiene el 10° término, es decir, la figura 10?

Como en los ejemplos anteriores, si quieres seguir creando términos debes ir dibujando de acuerdo a un patrón o regla de construcción; para lo cual debes observar con mucho detenimiento las características de los términos ya dibujados.

En esta sucesión, el primer término está formado por 1 círculo, el segundo por 4 círculos, el tercero por 9, el cuarto término por 16, el quinto término por 25 y finalmente el sexto término por 36.

Recuerda que, si elaboras algún registro que te ayude a tener presente la información que vas encontrando, podrás tomar mejores decisiones para encontrar la solución. En este ejemplo, si acomodas los números anteriores tienes la siguiente serie:

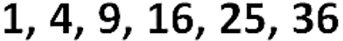
Al observar con atención los números presentados, ¿puedes identificar qué debes hacer con el primer número de círculos de la primera figura para poder dibujar la segunda?

Para comprenderlo mejor, observa cuántos círculos tiene cada una de las figuras en la base y en la altura de la figura:

¿Encontraste información nueva?, seguramente identificaste que a medida que hay un nuevo término a la derecha, la cantidad de círculos van aumentando 1, tanto en la base como en la altura de la figura, por lo que, ¿ya comprendiste cuál es la regla de construcción o diseño? La siguiente es una forma de expresarla:

Así, para responder a la pregunta de ¿Cuántos círculos tiene el 10° término o figura 10?, si observas con atención, el lugar que ocupa cada término coincide con el número de círculos que forman la base y la altura, por lo tanto, en la décima figura, la base del cuadrado tendrá 10 círculos y 10 círculos de altura, algo así:

Y si la nueva fila y la nueva columna deben completarse para formar un cuadrado, la figura 10 se vería de la siguiente manera:

Si ya comprendiste la regla ¿Cuántos círculos tendrán la base y la columna de la figura 15?

Analiza el siguiente ejemplo:

Como te puedes dar cuenta, en la parte de abajo, está la cantidad de círculos rosa que componen a cada término. ¿Puedes identificar la regla de construcción? ¿Qué va sucediendo con la cantidad de círculos a medida que van apareciendo los términos hacia la derecha?

Tal vez ya te identificaste que la regularidad o regla de construcción o diseño es:

Teniendo estos datos ¿Cómo podrías saber si la siguiente imagen pertenece o no pertenece a la sucesión?, toma en cuenta lo que ya sabes.

Haciendo el análisis, verás que sí pertenece a la sucesión éste término. Y sería el término 9. Esto se puede comprobar de dos maneras:

Dibujando la sucesión y tomando en cuenta el número de círculos que forma cada término
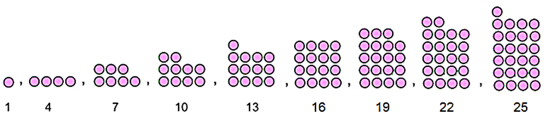
Analizando la serie de números: si los primeros 5 términos tenían 1, 4, 7, 10 y 13 círculos, los términos 6°, 7°, 8° 9° y 10° aumentarán en tres círculos cada uno, esto se puede observar mejor si aumentamos esa cantidad en cada caso: