Variaciones sobre un mismo tema
Variaciones sobre un mismo tema
Aprendizaje esperado: arma y desarma figuras en otras diferentes. Analiza y compara el área y el perímetro de la figura original, y la que se obtuvo.
Énfasis: identifica que el perímetro de una figura puede cambiar cuando se descompone en otras figuras, pero el área se conserva.
¿Qué vamos a aprender?
Recordarás las características de los polígonos, obtener el área y el volumen.
Aprenderás del origen del Tamgram y las figuras que se pueden formar con los 7 polígonos.
Formarás figuras distintas en las que cambia el perímetro pero el area se conserva.
¿Qué hacemos?
Conocerás un tema muy divertido e interesante que ya has trabajado con anterioridad, no solo en sexto grado, también en cursos anteriores, el área y el perímetro, ocurre algo interesnte que vas a trabajar en esta sesión.
El perímetro de una figura puede cambiar cuando se descompone en otras figuras, pero el área se conserva.
Siempre es interesante aprender cosas nuevas, recuerda que en una sesión anterior se trató el tema del perímetro, específicamente sobre el perímetro de un terreno que tenía que llenarse con cactus, y sobre las ofertas del cactus y la importancia de mencionar que el perímetro es el contorno de una figura.
Y así es, el perímetro es la suma de la longitud de cada uno de los lados de una figura, como estos son iguales mides en una sola dimensión. Recuerda también que en el área se miden dos dimensiones, el largo y el ancho de un polígono, cualquiera que sea, de manera que puedes obtener la superficie del polígono o la figura que estás midiendo.
Es importante que recuerdes lo que has aprendido, pero más importante aún, recordar cómo utilizar lo aprendido.
Es muy interesante conocer las historias que te cuentan sobre cosas que usas en el presente, pero fueron creadas y usadas en el pasado, el tamgram está compuesto por 7 polígonos.

Dos triángulos grandes, uno mediano y dos pequeños, dos cuadriláteros: un cuadrado y un paralelogramo, en total siete piezas.
Es importante mencionar algunas de las características que cumplen estas figuras que componen al Tangram, todas las piezas son simétricas, es decir si las cambias de posición siguen conservando su forma, a excepción del paralelogramo que si lo volteas cambia su orientación, por lo tanto el paralelogramo tiene dos opciones al utilizarse.
Esto de la geometría es muy interesante, entonces puedes formar además de figuras como personas, aviones y conejos, formas geométricas, como el cuadrado que se forma si juntas todas las piezas.
Puedes hacer un sinfín de formas geométricas y figuras de la vida cotidiana como lo proponían los chinos y como se ha estudiado desde hace muchos años. Hay otra característica que debes saber de los polígonos que conforman el tangram, los polígonos que hoy estás revisando, todos son convexos.
Recuerda que un polígono convexo, es aquel que todos sus ángulos internos son menores a 180° es interesante que conozcas todas las características que pueden tener los polígonos. Observa la siguiente imagen, te vamos a dar un dato más del Tangram.
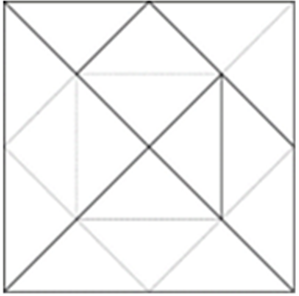
Si divides los polígonos del tangram puedes obtener 16 triángulos del tamaño de los dos más pequeños. ¿No te parece interesante? Seguramente ya quieres comenzar a formar figuras con el tangram.
Empecemos, y te pedimos por favor que vayas a a la página 155 de tu libro de desafíos matemáticos y recortes el Tangram que tienes ahí.

Comienza a armar una figura, pon mucha atención en la imagen tienes una figura que deberás replicar con tu tangram.

Necesitas los dos triángulos pequeños, el paralelogramo y el cuadrado. ¿Lograste replicarla? Has una figura más para poder comenzar con el desafío de hoy.

Ahora necesitas el cuadrado y los dos triángulos pequeños, ¿Listo? ¡Felicidades!
Ahora vas a comenzar con el desafío, y la consigna de hoy dice: Recorta las piezas del tangram de la página 155, reproduce las figuras que se muestran abajo y calcula su perímetro y área.

En casa ya tienes tu tangram recortado, empieza a armarlos, pero ¿Cómo sabrás las medidas de la figura? Puedes medir cada una de las figuras del tangram y así puedes sumar los lados que quedan en el contorno que es lo que forma el perímetro y de esa manera obtienes el perímetro de la figura que armaste. Comienza a medir cada una de las figuras.
Comienza a medir en tu libro las piezas del tangram, inicia con el paralelogramo que mide de un lado 4.2 y del lado más largo 6 cm ahora el triángulo 6 y de un lado 4.5 y del otro 4.5 cm.
No olvides colocar correctamente la regla para tomar correctamente las medidas, mientras lo haces te recordamos que debes obtener el perímetro de cada una de las figuras, corrobora que estén correctas.

Si ya tienes todas las medidas de cada uno de los polígonos del tangram, comienza con la figura más sencilla, el tangram armado como un cuadrado.
Ese será más sencillo porque las medidas de los cuatro lados son iguales entonces si tienes que el primer lado del triángulo morado mide 12 cm. los cuatro lados miden lo mismo ya que es un polígono regular, entonces 12 por 4 lados es 48 cm. El perímetro de esta figura es de 48 cm. ahora debes obtener el área. ¿Recuerdas la fórmula para obtenerla? La fórmula para obtener esta área: Lx L entonces será 12 por 12 es igual a 144 cm2 porque mides dos dimensiones largo y ancho, esto lo viste en la sesión en que medias las bases de los prismas.

¿Qué área obtuviste? ¿Tienes el mismo resultado? No olvides verificar tus respuestas y si es necesario corregir.
Ahora sigue con la próxima figura, ¿Qué te parece el gato? ¿Te gustan los gatos? Este ejercicio lo harás en tu libro, comenzarás sumando los lados 6 + 4.3 + 4.3 + 6+ y como el paralelogramo no está completo, entonces mide 1.7 cm + 4.3
El total es de 73.7 cm. como puedes observar, es muy grande el perímetro del gato comparado con el perímetro del cuadrado, el perímetro cambió mucho, al colocar los polígonos de diferente manera el perímetro cambia, entonces este puede variar dependiendo de la posición que tengan los polígonos que forman las figuras.
Cada vez que colocas los polígonos puedes colocar uno de sus lados afuera y medirá distinto.
Para que puedas obtener el área de esta figura, como no existe una fórmula para el área del gato debes obtener el área de cada una de las siete figuras e irlas sumando, así es lo mejor. Otra forma más sencilla es que consideres que si todas las figuras que forman el gato son las mismas que formaron el cuadrado, el área debe ser la misma, porque solo cambiaste de posición los polígonos, pero el área no la modificaste.
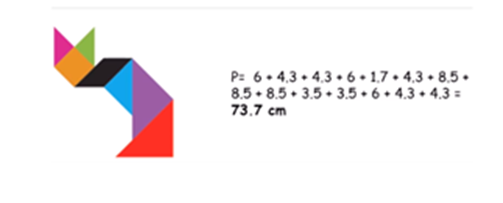
Sigues conservando la misma área ya que esta no se modifica al cambiar de posición, sus dimensiones son las mismas, por lo tanto como utilizaste los siete polígonos para formar el gato, el área es la misma del cuadrado 144cm2 y el perímetro de 73.7 cm.
El ejercicio que sigue será más sencillo, porque las áreas de las otras figuras serán las mismas solo tienes que medir el contorno para obtener el perímetro.

Ahora toca el ave, esta mide 12+4.2+4.3+4.3 da un total de 87.7 cm de perímetro y su área de 144cm2 como todas las figuras porque se conservan las áreas de todos los polígonos.
No olvides verificar que sean correctos, ya solo te queda una figura más por realizar.
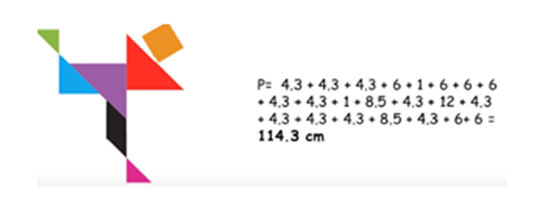
Es muy sencillo, sumas 4.3+4.3+4.3+6+1 da un total de 114.3cm este perímetro sí fue mucho mayor que los anteriores, pero el área sigue conservándose 144 cm2
Terminaste con el desafío de hoy y con la sesión también, hagamos un pequeño recuento de lo aprendido.
Recordaste las características de los polígonos, que pueden ser regulares porque todos sus lados son iguales.
Aprendiste también que cuando formas figuras distintas con los poligonos el perímetro de esta puede variar según la posición en la que lo coloques, pero su área se conserva.
Recordaste también que los polígonos te ayudan a formar cuerpos geométricos y las áreas de estos te ayudan a obtener el volumen.
Aprendiste muchas cosas nuevas, recordaste muchos momentos y aprendizajes de este ciclo y también de ciclos anteriores, además del reto de formar las figuras, pero sobre todo recordar la importancia del área, del perímetro y de conocer las fórmulas para obtenerlos.
Recuerda que todos los aprendizajes son importantes, pero el entusiasmo, la atención y constancia también lo son.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.