Un viaje por la región de las fracciones
Aprendizaje esperado: resuelve problemas que implican sumar o restar números fraccionarios con igual o distinto denominador.
Énfasis: resuelve problemas que impliquen sumar o restar fracciones cuyos denominadores son múltiplos uno de otro. Usa el cálculo mental para resolver adiciones y sustracciones con números fraccionarios.
¿Qué vamos a aprender?
Resolverás problemas que implican sumar o restar números fraccionarios con igual o distinto denominador.
¿Qué hacemos?
Continuarás con este viaje por contenidos estudiados que te permitirá fortalecer y afianzar los aprendizajes que adquirimos en quinto año.
Han estado muy interesantes los repasos que hemos hecho, porque así despejamos posibles dudas que hayan quedado el año pasado.
¿Qué te parece si iniciamos este viaje?
¿En esta ocasión a dónde iremos?
Iremos al mundo de EL SENTIDO NUMÉRICO y PENSAMIENTO ALGEBRAICO que, como recordarán, habíamos dicho que sería un mundo en el que estaríamos frecuentemente, ahí visitaremos la región de las fracciones y los decimales.
Abróchense los cinturones que allá vamos.
Ya estamos aquí y aprovecharemos para introducirnos un poco acerca de los números fraccionarios. Recuerdas, ¿Cuáles son?
Son los números que nos permiten expresar y representan partes de una cantidad entera.

El concepto de fracción se dice que viene de la traducción al latín que se hizo del libro de aritmética de Abu Abdallah Muḥammad, conocido como Al-Juarismi.
Fue un gran matemático persa que sentó las bases del álgebra y usó la palabra fractio para traducir la palabra árabe al-kasr que significa quebrar o romper.
También se considera que a él se debe la introducción de sistema de numeración que nosotros usamos y ya que estamos en el mundo de los números te podrás dar cuenta que los números naturales son muchos, son una infinidad, por ejemplo, cuando medimos o comparamos algo no suele constar de un número exacto de unidades, sino que, frecuentemente, hay que recurrir a partes o fracciones de esas unidades para dar una medida más exacta.
Se mencionó que eran una parte del entero, pero recuerdo que existen fracciones que representan más de un entero.
Por ejemplo, las fracciones mixtas o números mixtos que están formados por una parte entera y una fracción y que son equivalentes a lo que conocemos como fracción impropia.
En grados anteriores has estado trabajando con fracciones, números decimales y naturales.
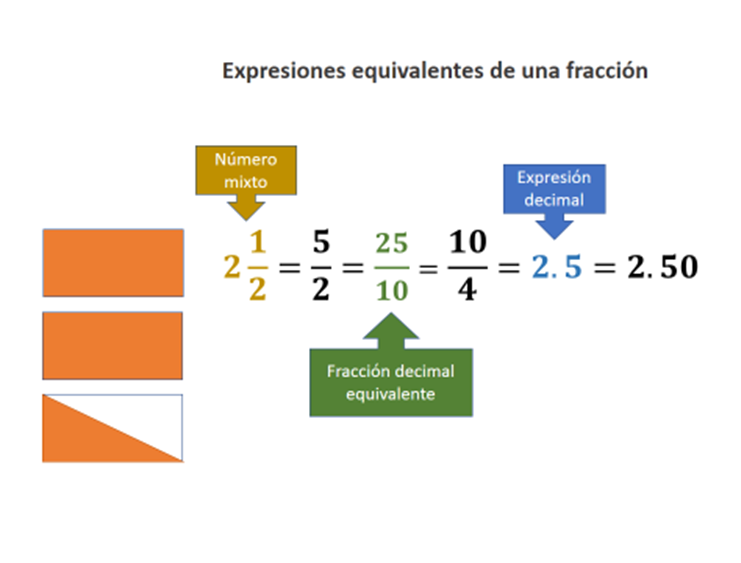

Y sabes que una fracción se puede expresar como un decimal o expresar con fracciones equivalentes.
Ya que estamos repasando podemos recordar que las fracciones que tienen como denominador 10, 100, 1 000, diez mil, etc., se llaman fracciones decimales.
Es importante que comprendas que puedes utilizar una expresión equivalente de una fracción o de un número decimal en todo momento y que eso les permitirá resolver diversos problemas.
Viajaremos en el tiempo para observar y recordar un fragmento de una sesión de Aprende en casa de quinto grado donde nuestros alumnos que ahora están ingresando a sexto tuvieron oportunidad de ver cómo se transforman las fracciones que tienen distinto denominador a fracciones equivalentes con igual denominador, para poder sumarlas o restarlas.
Eso sería muy bueno regresar en el tiempo para volver a ver un contenido de su clase del año pasado, seguro en algunas ocasiones quisiéramos poder revivir un momento.
Observa la sesión de la maestra Andrea y después retomemos su estrategia para verificar la equivalencia de fracciones y resolver otra situación.
- La gelatina de Mariana. Del 13´47” al 19´44”
https://www.youtube.com/watch?v=0jTkRGXZCXA
¿Qué te pareció, ya refrescaste tu memoria? Alguien que me había comentado que le interesaba recordar, en particular, acerca de cómo sumar o restar fracciones es Alejandra y hoy la invité a participar con nosotros.
Estábamos viajando en el tiempo para recordar cómo sumar o restar cuando las fracciones tienen denominadores diferentes.
Según recuerdo se convierten a fracciones equivalentes, pero con igual denominador.
Así es y una vez que tienen igual denominador, sólo queda sumar o restar los numeradores, de esa manera podemos resolver las sumas o restas de fracciones.
Y cuando los denominadores sean diferentes, una recomendación que no debemos olvidar es que debemos fijarnos si uno de ellos es múltiplo de otro u otros denominadores, porque eso nos permitirá expresar las fracciones en fracciones equivalentes a partir de ese denominador que es múltiplo de los otros. Hagamos una resta mentalmente les parece.
Pongamos a trabajar el cerebro.
Veamos si podemos lograrlo.
Ocho novenos menos dos tercios.
Se observa que 9 es múltiplo de 3 por lo que tengo que ver qué número multiplicado por tres me da nueve.
Es el 3
Entonces multiplicaremos numerador y denominador de la fracción dos tercios por 3 para obtener una fracción equivalente de expresada en novenos.
Entonces 2 por 3 es 6 ese es ahora el numerador y 3 por 3 son 9 así que la fracción equivalente a dos tercios es seis novenos.
De esa manera igualamos los denominadores de ambas fracciones a novenos.
Ahora podemos hacer la resta directamente fijándonos sólo en los numeradores, ocho novenos menos seis novenos.
Y nos da dos novenos.
Hacemos el mismo procedimiento para la suma que para la resta de fracciones.
Te propongo, si conservas tu libro de texto de Matemáticas quinto grado buscarlo. Yo sé que están emocionados por conocer y usar sus nuevos libros, pero una manera de viajar al pasado es retomando nuestro libro anterior y revisar las situaciones que resolvimos.
Cuando hojeamos el libro podemos recordar cómo y por qué anotamos una respuesta.
O nos permite volver a pensar de qué manera llegamos a ese resultado.
Nuestros libros anteriores se convierten en fuente de información para nosotros, por ejemplo, primer desafío del libro de quinto, justamente, corresponde a una situación que implica sumas y restas de fracciones.
Puedes comenzar leyendo la consigna de este desafío.
Lee el contenido de la tabla del desafío 1 ¿Cuánto es en total?
Para preparar sopas se empleó medio kilogramo de queso Oaxaca. Para quesadillas se empleó cuatro sextos de kilogramo de queso Oaxaca y medio kilogramo de queso Chihuahua. Para aderezos se usaron siete octavos de kilogramo de queso Chihuahua y para preparar botanas se usaron un tercio de kilogramo de queso Oaxaca y tres cuartos de kilogramo de queso Chihuahua.
¿Cuánto queso Oaxaca se usó al término del día?
¿Cómo podemos contestar esta pregunta?
Sumando todas las fracciones de la columna que dice queso Oaxaca.
Entonces qué cantidades debemos sumar.
Para preparar sopas se empleó medio kilogramo de queso Oaxaca más cuatro sextos de kilogramo para quesadillas más un tercio de kilogramo para botanas.
Y ahora, ¿Qué se hace?
Convertir a fracciones equivalentes y que tengan el mismo denominador, pero antes podemos identificar si un denominador es múltiplo de los otros denominadores y todos los convertimos a ese denominador.
En este caso el denominador que es múltiplo de los otros dos es el seis que representa sextos.
Entonces cuáles serían las fracciones equivalentes a un medio y a un tercio expresadas en sextos.
Un medio serían tres sextos.
Y de un tercio serían dos sextos.
Escribe la suma de fracciones en sextos.
Tres sextos de kilogramo más cuatro sextos de kilogramo más dos sextos de kilogramo.
Ahora sólo queda sumar los numeradores para dar el resultado en sextos.
El total es nueve sextos de kilogramo de queso Oaxaca.
Y de qué otra forma podemos expresar ese total.
El total es más de un kilogramo, entonces es un kilogramo y tres sextos de kilogramo.
Este resultado también es equivalente a un kilogramo y medio, porque tres sextos son equivalentes a un medio, como ya vimos.
Así que, en la cocina, siempre sabroso, emplearon un kilogramo y medio de queso Oaxaca.
De manera semejante podemos saber cuánto queso Chihuahua se utilizó.
Te invito a seguir contestando las otras preguntas de este desafío que implican sustracciones y adiciones con fracciones, para refrescar todo ese conocimiento que ya tienen, durante sus clases de sexto grado estaremos trabajando con este tipo de problemas y en particular la equivalencia de fracciones.
Ahora ya sabemos que las fracciones jugarán un papel importante en este curso.
¡Oh no! ¡Fracciones! mi quebradero de cabeza.
No, no te preocupes si vamos paso a paso lo vamos entendiendo mejor, además, debemos reconocer su importancia, porque recuerden que cuando hacemos cosas tan cotidianas como medir o comparar surge la necesidad de utilizarlas, por eso les quiero hacer un poco de historia sobre cómo surge su representación como partes de una unidad. Éstos se remontan a casi 4 000 años atrás, en la cultura babilónica. Los babilonios eran expertos en cálculos, y se considera que fueron ellos quienes por primera vez representaron y utilizaron las fracciones.
Las fracciones ya aparecen en los primeros textos matemáticos de los que hay constancia tiempo después. Quizás uno de los más antiguos y más importantes sea el Papiro de Rhind de Egipto, escrito hacia el año 1 650 a. C. y que se considera la mayor fuente de conocimiento de la matemática egipcia y, por eso, durante este ciclo escolar haremos referencia a ese documento y, también es una muestra de la importancia de conservar documentos, libros y, claro, actualmente videos y audios.
Las fracciones eran conocidas por los babilonios, egipcios y griegos.
Los egipcios resolvían problemas de la vida diaria mediante operaciones con fracciones, entre ellas la distribución del pan, el sistema de construcción de pirámides y las medidas utilizadas para estudiar la tierra.
Eso que mencionas lo podemos comprobar en numerosas inscripciones antiguas como el Papiro de Ahmes, en esta ocasión no viajaremos a Egipto, les tengo reservado para el final de la clase otro viaje, por el momento los invito a que viajemos a otra clase de quinto grado. - Frutas de temporada. Del 9´54” al 12´22”
https://www.youtube.com/watch?v=zn9BIBBajWA
Esta suma implicó hacer sumas y restas mentalmente, lo importante es ver la practicidad de igualar los denominadores con una fracción equivalente para que podamos resolver fácilmente una suma o una resta de fracciones.
Ahora veamos un problema que implica suma y resta de fracciones. - Frutas de temporada. Del 12´20” al 15´13”
https://www.youtube.com/watch?v=zn9BIBBajWA
Las fracciones nos permiten medir de una manera más exacta, al igual que los números decimales.
Cuando veamos fracciones con diferente denominador si ya sabemos su equivalencia podemos hacer las operaciones hasta mentalmente, pero si se nos complica podemos hacerlo en forma escrita.
Cuando debemos contar, medir o repartir y los números naturales no sean suficientes, podemos recurrir a los números decimales o a las fracciones, para representar todas las situaciones cotidianas y por eso tenemos este tipo de números. Conforme avancen en sus estudios conocerán otros números, mientras tanto, nosotros en sexto grado también continuaremos estudiando los naturales, decimales y fraccionarios.
Es muy interesante ver cómo desde la antigüedad existen estos números para resolver la necesidad de repartir dinero o tierras, y para pagar tributos o impuestos, esa relación entre la parte y el todo es la que expresamos con números decimales o con números fraccionarios.
Todos estos viajes a los conocimientos pasados nos permiten conocer de dónde salen los números que conocemos, cómo se generaron cómo se han usado, los tipos de problemas que han permitido resolver y cómo llegan hasta nosotros.
Viajar en el tiempo nos permite conocer desde qué épocas ya se empezaron a poner en práctica tantos conocimientos que en la actualidad nos permiten encontrar más fácilmente muchos resultados.
Anteriormente mencionamos que los primeros en emplear los números fraccionarios fueron los babilonios, los egipcios y los griegos, me gustaría que hiciéramos un último viaje.
Una ciudad del Mediterráneo en Egipto, que fue fundada por Alejandro Magno y conoceremos un poco acerca de quién fue Hipatia.


Hipatia estudió el movimiento de diversos cuerpos celestes.
En un documental mencionan como la primera mujer matemática y como dice Ale con estudios de astronomía.
Efectivamente sus aportes son muchos las y los invito a que conozcamos un poco acerca de su vida en la próxima sesión.
Las matemáticas están en muchas cosas que nos rodean.
Pues esto es sólo una probadita de todo lo que te espera este ciclo escolar.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Consulta los libros de texto en la siguiente liga.
