Todos dentro de la circunferencia
Todos dentro de la circunferencia
Aprendizaje esperado: cálculo de la longitud de una circunferencia mediante diversos procedimientos.
Énfasis: usar la relación entre la circunferencia y el diámetro para resolver problemas.
¿Qué vamos a aprender?
Recordarás y usarás lo que viste acerca de cómo calcular la circunferencia de un círculo.
¿Qué hacemos?
Vas a jugar “ahorcado” ¿Lo has jugado? Imagina que la elección de las letras la haces tú. ¡Comienza!
La palabra tiene 14 letras.

Es una palabra larga. La primera letra elegida es la letra A escribe la letra A en la última línea, la última letra de la palabra es una A
Ahora una E y hay 2 la octava y en la décima línea. Ahora una consonante, si eliges una, por ejemplo, la N y no hay ninguna en la palabra, entonces corresponde dibujar la cabeza del ahorcado. La otra consonante elegida es la R y sí, hay 2 en la tercera y en la novena posición. ¿Crees que tenga la letra O? No, no hay, entonces dibuja una línea que simule el cuerpo del ahorcado.
Aún faltan muchas letras, vocales también, entonces una letra I. Sí hay dos I, la segunda y la penúltima. A ver qué dice:
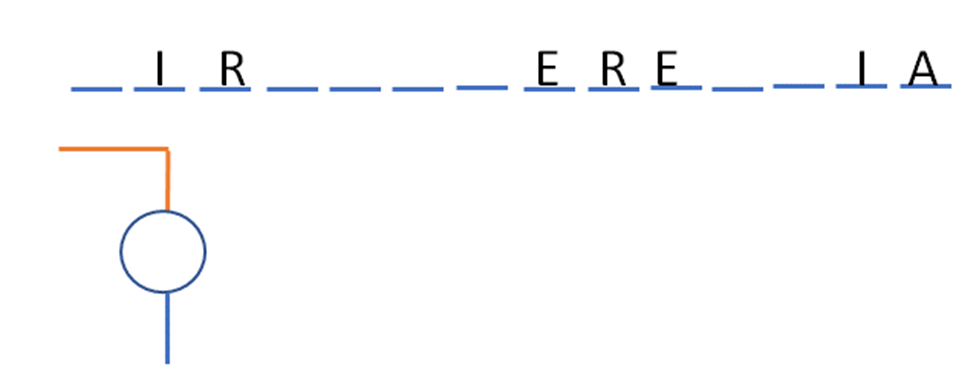
¿Ya encontraste la palabra? ¿No, qué te parece una L? No hay L dibuja un brazo al ahorcado.
Ahora hay que probar usando letras de conceptos matemáticos si de eso se trata la sesión, por el momento la siguiente consonante será N y es una consonante muy bien elegida porque la palabra relacionada con lo que hoy trataremos tiene dos N en la sexta y en la undécima línea.
¿Ya la pudiste relacionar con un concepto matemático? Ahora seguiría una D y como no hay D dibuja la otra mano, sólo faltan las piernas, así que trata de pensar conceptos matemáticos, la palabra está relacionada con la forma, el espacio y la medida.
Podría ser la letra C relacionada con el círculo, un concepto matemático.
Muy buena letra hay tres letras C es la primera letra, la cuarta y la antepenúltima.
¿Ya encontraste la palabra? Circunferencia.

En esta clase recordarás y usarás lo que viste acerca de cómo calcular la circunferencia de un círculo.
Recuerdas la receta que le dio el doctor compás al círculo que estaba angustiado al no saber con exactitud el valor de su circunferencia, ya que PI es un número con una cantidad infinita de cifras decimales, pero le recomendó que usará el valor aproximado de PI de 3.1416
Bueno, recuerda que el valor de la circunferencia de cualquier círculo lo puedes determinar multiplicando la medida de su diámetro por ese valor aproximado de Pi 3.1416 ya que la circunferencia mide, aproximadamente, tres veces su diámetro y un pedacito más que es inconmensurable, es decir, que no es posible medir de manera exacta.
¿Sabes qué quiere decir inconmensurable? Inconmensurable es una palabra que proviene del latín, incommensurabĭlis, es un adjetivo que significa enorme, que por su gran magnitud no puede medirse o es imposible de medir, en el caso de PI por lo menos hasta ahora no se conocen todas las cifras decimales que tiene. Recuerda que hay hasta concursos para decir el mayor número de cifras decimales de Pi.

https://libros.conaliteg.gob.mx/P6DMA.htm?#page/126
Y en el programa relacionado con el desafío 67 ¿Para qué sirve Pi? resolviste diferentes problemas, en uno faltaba el dato del diámetro, en otro tenías que obtener la circunferencia, y en otro recuerda que pusiste en juego más habilidades, porque determinabas las vueltas que daban las ruedas de una bicicleta en un determinado trayecto. Observa un poco de ese programa.
- Programa P6_35.89. #AprendeEnCasa III. 6º Primaria. Matemáticas. Pi, la letra y el número 26 de mayo 2021
https://www.youtube.com/watch?v=7mFliWuYUJ4
Recuento de lo que viste en las sesiones relacionadas con la medida de la circunferencia, el diámetro y PI ahora repasarás poniendo en práctica lo que aprendiste en esas sesiones.
Comienza leyendo una noticia tomada de una revista. Es un pequeño fragmento del artículo: “El cráter de la muerte”.
¿Qué te pareció? Estamos seguros de que te agradó, siempre es importante que se sigan analizando hallazgos que sucedieron hace millones de años.
Observa la forma que dejó el meteorito que se impactó, quedó un gran círculo, bueno, un gran hoyo, pero en la vista aérea se observa como un círculo.
El artículo decía que tiene un diámetro aproximadamente de 200 kilómetros, calcula la circunferencia de este cráter, ¿Recuerdas cómo se calcula? Aquí es cuando debes usar el valor aproximado de Pi que es 3.1416 porque debes multiplicar los 200 kilómetros de diámetro del cráter por el valor de Pi para obtener la medida aproximada de la circunferencia que dejó el cráter. Has el cálculo con ayuda de tu calculadora, pero antes has una estimación de la medida de la circunferencia. ¿Estás de acuerdo? Te ayudamos un poco.
Considera que 200 es dos veces cien, es decir, 2 por 100 entonces, ¿Podrías pensar en el doble de PI por 100? El doble de Pi es 6.2832 y ese número por cien, significa recorrer el punto decimal dos posiciones a la derecha, entonces es 628.32
Qué te parece si ahora lo compruebas con tu calculadora. Teclea 3.1416 por 200 y te da como resultado 628.32 entonces, en el contexto de lo ocurrido en la formación del cráter, la circunferencia que dejó el impacto del meteorito es de 628 kilómetros más 320 metros. ¡Qué grande!
Ahora leerás una versión de la leyenda “Los cráteres de la Luna”.
¿Qué opinas de esta leyenda? Es importante la reflexión del cuidado del ambiente y que la explotación de los recursos naturales debe ser sustentable, no podemos usar solo por usar. Te proponemos que ahora determines el diámetro de uno de los cráteres de la Luna.
Calcula el diámetro que tendrá uno de los cráteres de la Luna. El cráter Leibnitz mide 769.6920 kilómetros de circunferencia aproximadamente, ¿Cómo puedes obtener el valor de su diámetro? Recuerda que contestaste un problema parecido en uno de los desafíos, pero donde pudo haberte quedado muy clara la relación que existe entre la circunferencia y el diámetro fue cuando mediste la circunferencia y los diámetros de varios objetos circulares.
Recuerda que fuera cual fuera el objeto de forma circular que consideraras, al dividir la medida de su circunferencia entre el tamaño de su diámetro, siempre te daba como resultado un valor aproximado a 3.1416 así, por ejemplo, si ya sabes que la circunferencia se obtiene multiplicando el diámetro por 3.1416 entonces cuando falta el diámetro, si conoces la medida de la circunferencia, solamente debes dividir la medida de su longitud entre 3.1416
Divide en la calculadora los 769.6920 kilómetros entre 3.1416 te debe dar 245 kilómetros, entonces el diámetro del cráter Leibnitz que está en la Luna mide 245 kilómetros.
Observa la siguiente imagen, ¿La reconoces?
Es la rueda de la fortuna llamada la Estrella de Puebla, la viste en una de tus sesiones.
Ahora, lee la siguiente información.
Con esta información, contesta un último problema que dice así:
Para iluminar ambas circunferencias de la rueda se usaron 438.56736 metros de series de focos, ¿Con este dato podrías saber cuánto mide su diámetro?
De acuerdo con lo que has visto, primero tendrías que sacar la mitad de los metros de la serie de focos para saber el tamaño de la circunferencia de uno de los dos aros que forman la rueda donde se sostienen las sillas.
Has la operación con la calculadora, para saber cuánto mide la circunferencia 438.56736 entre 2 es igual a 219.28368 eso mide la circunferencia de cada uno de los aros y con ese dato puedes obtener el diámetro de una circunferencia, dividiendo 219.28368 entre 3.1416 que da como resultado 69.8
Justo esa es la medida del diámetro que tiene la rueda de la fortuna. Has puesto en práctica en este repaso lo que habías aprendido acerca de la relación entre el diámetro y la circunferencia.
Te tenemos preparada una cápsula que grabó Carola donde resolvió un problema en el que aplicó lo que aprendió en las clases sobre Pi y la circunferencia. Vamos a verla. - Cápsula de Carola.
(del minuto 21:56 al minuto 24:37)
Recuerda que debes poner en práctica tus conocimientos para que te permitan resolver problemas matemáticos tuyos o de tus familiares, así como reflexionar con otras personas las estrategias que podrías seguir, como lo hizo Carola.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas
