Tarjetas decimales

Tarjetas decimales

Aprendizaje esperado: uso del cálculo mental para resolver sumas o restas con números decimales.

Énfasis: ejercitar el cálculo mental de sumas y restas de números decimales y aplicar estrategias que les faciliten dichos cálculos.

¿Qué vamos a aprender?

Jugarás con el cálculo mental, pero no como estás acostumbrado (con números enteros). Ahora realizarás sumas y restas con números decimales. ¿Qué te parece?

¿Qué hacemos? 

Antes de conocer el juego vas a recordar un poco sobre los números decimales.

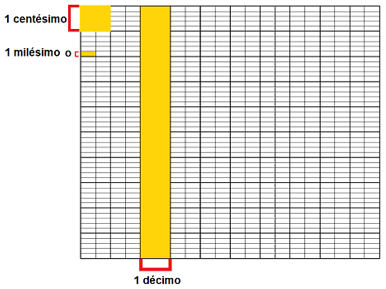
Recuerda que, en los números enteros, mientras más a la izquierda se encuentre un dígito, mayor es su valor posicional y, en el caso de los decimales, entre más cerca se encuentre un dígito del punto decimal su valor es más próximo a una unidad.

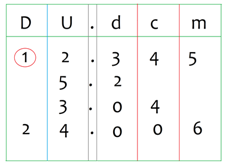
Por ejemplo, aquí el 1 tiene un valor posicional de 10.

En el caso de los decimales .3 o sea 3 décimos equivale por ejemplo a 30 centésimos o 300 milésimos.

Si quieres realizar sumas o restas, como, por ejemplo:

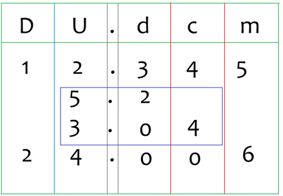
5.2 – 3.04 aparentemente no se puede porque te faltaría un digito, pero recuerdas. ¿Cómo puedes hacer esa resta?

Le puedes agregar a la derecha un 0 al 2 y quedará como 5.20 que es una escritura equivalente a 5.2

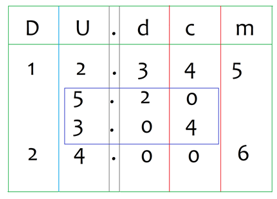
Ahora sí, puedes hacerlo mentalmente: como a 0 no le puedes quitar 4 entonces, toma 1 décimo que es igual a 10 centésimos y le resto 4 lo que te da 6 centésimos; ya no tienes 2 décimos porque tomaste 1, así que 1- 0 = 1 y por último 5 -3 = 2 y tu resultado sería 2.16

Recuerda, para realizar cualquier resta en la que intervengan números decimales, sólo debes alinear las cantidades con relación al punto decimal y hacer la operación como ya sabemos.

Ve a tu libro de texto “Desafíos Matemáticos” páginas 58 y vas a leer las indicaciones de lo que debes hacer.

En equipos nombren a un juez o árbitro en cada uno y jueguen lo siguiente con el material recortable, páginas 239 y 241.

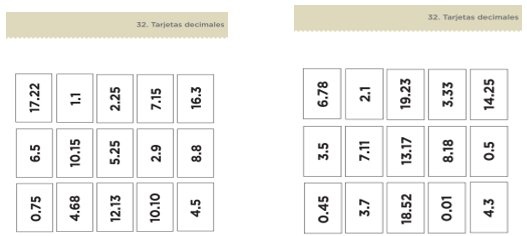
Cada equipo tiene dos mazos de 15 tarjetas cada uno. El árbitro colocará un mazo a su derecha y otro a su izquierda. Todas las tarjetas deben tener el número hacia abajo.

Muy bien, aquí tengo mis tarjetas recortadas, 15 en un mazo y 15 en el otro, uno a mi izquierda y otro a mi derecha con los números hacia abajo.

El árbitro tomará una tarjeta del mazo que está a su derecha y la mostrará al resto del equipo; después tomará una tarjeta del mazo que está a su izquierda y también la mostrará. Enseguida, otra vez volteará las tarjetas hacia abajo.

Aquí está mi primera tarjeta. ¿Qué número es?

Es .75 que se lee 75 centésimos.

Y esta es la segunda.

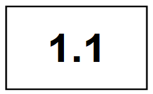
Esta tarjeta se lee como 1 entero, 1 décimo.

Continúo leyendo, “los demás integrantes del equipo harán mentalmente la operación que sea necesaria (suma o resta) para pasar del primer número mostrado el segundo.

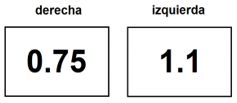
Esto quiere decir que debes analizar cuál número es menor y cuál mayor. ¿El primero (del mazo derecho) o el segundo (del mazo izquierdo)? así determinaremos si se realizará una suma o una resta.

Es muy fácil, el .75 es menor que 1.1

Entonces si quieres que de .75 se pase a 1.1 y ya sabes que el .75 es menor. ¿Qué operación debes realizar?

Se debe agregar, es decir vas a sumar.

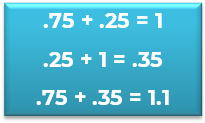
Si tienes .75 para llegar al entero debe sumar .25 y entonces te dará 1, pero quieres tener 1.1 así que tienes que sumar .1 más, por lo que .25 + 1 = .35

La respuesta es sumar a .75, .35 para pasar a 1.1

Eso que hiciste fue una descomposición aditiva, es decir representar un número, en este caso mediante la suma de otros dos. Yo terminaré de leer las indicaciones.

El primero que dé el resultado correcto se lleva las dos tarjetas, y ahora él será el árbitro. Para saber si el resultado es correcto, el árbitro puede hacer la operación con la calculadora o con lápiz y papel.

El juego finaliza cuando se terminan las tarjetas de los dos mazos, y gana quien haya logrado reunir más tarjetas.

Para saber si es correcto verificaras la operación.

Quiere decir que es correcto lo que nos dijiste, porque recordemos que 1.1 es igual que 1.10 o 1.100

Entonces, si esto no fuera un ejemplo. ¿Yo habría ganado las dos tarjetas y ahora me tocaría ser el juez?

Así es, tú puedes ser ahora el juez, ponemos las tarjetas hacia abajo y vamos a jugar con la ayuda de algunos niños y niñas que nos ven desde casa, para facilitar el proceso traigo sus nombres anotados en una tabla en la que iremos registrando la información necesaria.

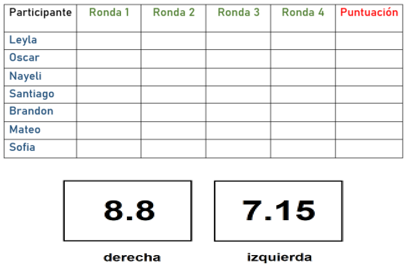
Es decir, que debes pasar del 8.8 al 7.15

Tienes las siguientes respuestas.

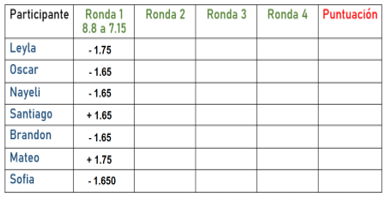
Tomaras las diferentes respuestas que dieron estos alumnos y alumnas y verificaremos quién tiene razón. Para empezar, veamos, ¿El número al que deseamos pasar, indicado en la segunda tarjeta, es mayor o menor?

Es menor.

Eso significa que al primer número debemos restarle una cantidad para obtener el número mostrado en la segunda tarjeta, por lo tanto, los que digan suma están descartados, y tenemos 3 respuestas diferentes indicadas con resta.

Realiza las 3 operaciones posibles para verificar la respuesta.

En estas tres operaciones ves espacios vacíos, en los que colocaras respectivamente un 0 ya que no afecta las cantidades representadas porque se trata de una escritura equivalente, así por ejemplo tienes 8 enteros con 8 décimos y al agregarle el 0 a la izquierda de los décimos, escribirías 80 centésimos ya que habrías dividido en 10 cada décimo, de manera que las operaciones quedarían así.

Al realizar la resta el resultado es.

7.05 ¿Este es el número al que deseábamos llegar? No.

Entonces descartamos esta respuesta. La siguiente operación es 8.8 – 1.65, vuelves a agregar el cero para no confundirte y realizas la operación, el resultado es 7.15 ¿Este es el número al que deseábamos llegar?

Sí, restar 1.65 es la respuesta correcta.

¿Estás seguro?

Ya dudé con su pregunta, déjame ver… oh ya entendí, dijimos que 8.8 es lo mismo que 8.80 u 8.800 eso quiere decir que la respuesta correcta es menos 1.65 o también puede ser menos 1.650 ya que 7.15 y 7.150 son la misma cantidad, escrita de forma un poco distinta.  Exacto.

Esto significa que tres alumnos proporcionaron respuestas correctas.

Así es, continua con la segunda ronda. Las siguientes tarjetas son:

Observa las respuestas de los alumnos y alumnas.

Tienes las siguientes respuestas.

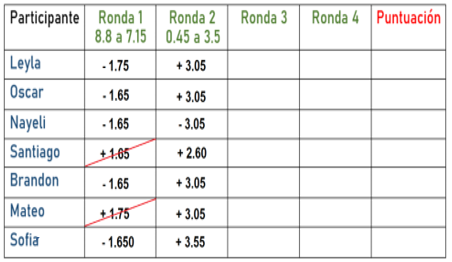
En esta ocasión como el segundo número, es decir, al que queremos llegar es mayor que el primero, debemos hacer una suma, así que, si alguien dijo resta, es errónea la respuesta.

De los que propusieron una suma, realizaremos las 3 operaciones posibles para verificar la respuesta.

3.50 ¿Este es el número al que deseabas llegar?

Sí, sumar 3.05 es la respuesta correcta.  ¡Exacto!

Finalmente es obvio que el resto de las operaciones nos dan un resultado distinto al que buscas.

Así es, vamos con la tercera ronda.

Pasaras del 0.5 al 7.11

Vamos con las respuestas de los alumnos y alumnas.

Tienes entonces las siguientes respuestas.

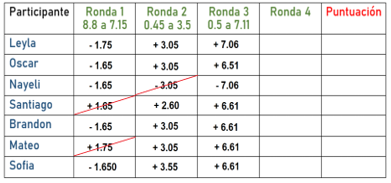
Nuevamente es una suma ya que el primer número es menor que el segundo, así que nuevamente descartamos las respuestas que dicen resta.

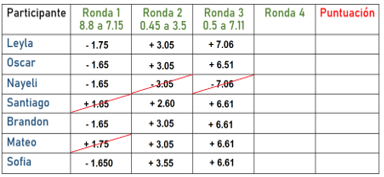
De los que propusieron una suma, realizarás las 3 operaciones posibles para verificar la respuesta.

En estas tres operaciones ves un espacio vacío en el primer sumando con relación al segundo, ahí puedes escribir un 0, ya que no afecta la cantidad representada porque se trata de una escritura equivalente; así tienes 5 décimos y al agregarle el 0 a la izquierda de los décimos, escribirías 50 centésimos, ya que habrías dividido en 10 cada décimo, de manera que las operaciones quedarían así.

7.56 ¿Este es el número al que deseábamos llegar? No.

Entonces descartas esta respuesta. La siguiente operación es 0.50 + 6.51 al realizar la operación, el resultado es 7.01 ¿Este es el número al que deseabas llegar? No.

Entonces descartas la segunda respuesta. La siguiente operación es 0.50 + 6.61 al realizar la operación, el resultado es 7.11 ¿Este es el número al que deseabas llegar?

Sí, entonces sumar 6.61 es la respuesta correcta.

Vas por la última ronda.

Queremos pasar de 3.7 a 2.25 vamos a ver qué nos proponen nuestros alumnos y alumnas.

Tenemos registradas las siguientes respuestas.

Bien, quieres pasar de 3.7 a 2.25 vas a ver qué nos proponen nuestros alumnos y alumnas.

Tenemos registradas las siguientes respuestas.

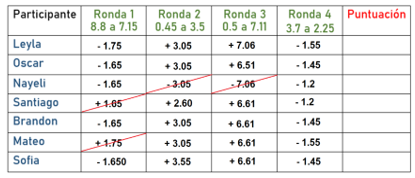
Analizaras, como has estado haciendo, si es suma o resta: si pasaras de 3.7 a 2.25 debes realizar una resta, ya que el segundo es menor.

Todas las niñas y los niños propusieron una resta, ahora vas a ver cuál es el resultado correcto.

En dos de las tres operaciones ves una diferencia de cifras con relación al minuendo, ahí puedes escribir un 0 ya que no afecta la cantidad representada porque se trata de una escritura equivalente, así tienes 7 décimos y al agregarle el 0 a la izquierda de los décimos, escribirías 70 centésimos ya que habrías dividido en 10 cada décimo, de manera que las operaciones quedarían así.

2.15 ¿Este es el número al que deseabas llegar? No.

Entonces descartas esta respuesta.

La siguiente operación es 3.70 – 1.45 al realizar la operación, el resultado es 2.25 ¿Este es el número al que deseábamos llegar?

Sí, entonces restar 1.45 es la respuesta correcta.

Ahora veremos quién fue la ganadora o el ganador.

Con cuatro aciertos, Brandon es el alumno que obtuvo más éxito al aplicar sus estrategias de cálculo.

El día de hoy ejercitaste el cálculo mental de sumas y restas de números decimales mediante un juego de tarjetas con números decimales.

Además, viste estrategias que nos pueden facilitar realizar dicho cálculo mental, espero puedan realizar este juego en casa con mamá, papá, hermanos, hermanas, para que todos practiquen el cálculo mental.

Los materiales se encuentran en su libro de texto, en los materiales recortables.

¡Buen trabajo!

Gracias por tu esfuerzo.