Sigamos dividiendo
Sigamos dividiendo
Aprendizaje esperado: conversión de fracciones decimales a escritura decimal y viceversa. Aproximación de algunas fracciones no decimales usando la notación decimal.
Énfasis: identificar que dividir el numerador entre el denominador es una manera de hallar la expresión con punto decimal de una fracción.
¿Qué vamos a aprender?
Aprenderas a realizar la conversión de fracciones decimales a escritura decimal y viceversa, también desarrollarás la aproximación de algunas fracciones no decimales usando la notación decimal, y podrás identificar que dividir el numerador entre el denominador es una manera de hallar la expresión con punto decimal de una fracción.
Vas a necesitar tu libro Desafíos sexto grado, desafío 56, página 113, tu cuaderno u hojas para tomar notas, lápiz, goma, sacapuntas y mucha disposición.
https://libros.conaliteg.gob.mx/P6DMA.htm?#page/113

¿Qué hacemos?
En esta sesión continuarás con el desafío de los listones, ¿Recuerdas qué características tenían las partes en las que cortamos cada tira? Sí, teníamos que dividir cada tira en partes iguales, por ejemplo, una tira de un metro de longitud la dividimos en 2 partes iguales y, otra más, en 4 partes, exacto, cortamos esos listones en medios y cuartos.
¿Y recuerdas también algo de lo que trató el video de la sesión pasada? Hablaba sobre fracciones decimales que son las que tienen como denominador 10, 100 o 1000. Bueno no sólo 10, 100 o 1000, también podría ser 10 000. 100 000, etc., y también se dijo que las fracciones decimales se pueden representar con números decimales. ¿Recuerdas algún ejemplo?
Por ejemplo.
Ambas se leen como un entero cinco décimos.
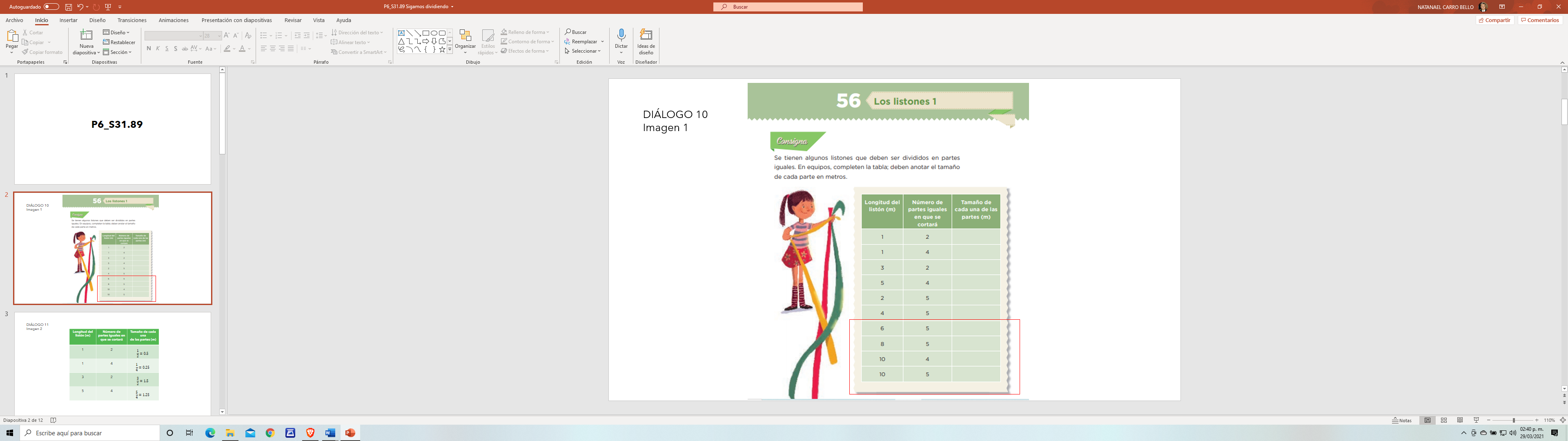
Esto se relaciona con el desafío número 56 llamado “Los listones 1” que ya habías comenzado a trabajar en la página 113

Recuerda que ya habías contestado los cuatro primeros renglones de la tabla.

Actividad 1
Comienza considerando la información de la fila 5

Dice que tomes 2 metros de listón y los partas en 5 partes iguales. En esta ocasión primero corta cada metro y luego divide cada metro en cinco partes iguales.
Recuerda que las 5 partes de cada metro deben tener el mismo tamaño, ya están aquí los dos metros divididos en cinco partes.
Cada parte corresponde a una quinta parte del metro, es decir, representan un quinto de metro.

Y como tienes dos metros de listón, ¿Cuántos quintos tienes en total? Tienes diez, diez tramos de 1 quinto de metro. Obtuviste diez quintos de los dos metros de listón.
¿Cuántas partes forman una quinta parte de los dos metros? Toma un quinto de cada metro y, tendrás ¡dos quintos!
Debes tomar una quinta parte de cada metro, para saber cuánto miden dos quintos de todo el listón que tenías inicialmente y que medía 2 metros.
¿Cómo piensas que se puede representar con otra expresión, la longitud de 2 quintos de este listón? Para encontrar otra forma de representarlo observa la imagen siguiente:

Cada metro equivale a 100 centímetros, si los divides en cinco partes iguales, cada parte entonces mide 20 centímetros, es decir, cada quinta parte del metro mide 20 cm, pero tienes que son dos quintas partes, porque eran dos metros, entonces serán 40 cm lo que mida la quinta parte de los dos metros.
Efectivamente, en este caso, 40 cm es equivalente a dos quintas partes de los dos metros originales, recuerda que, si quieres expresar estos 40 centímetros en metros, ¿Qué debes hacer? cuando se convierte una unidad de medida menor a una mayor, hay que dividir, entonces 40 centímetros los tendrías que dividir entre 100 para que la expresión quede en metros.
Así es, se puede decir 40 centímetros, o bien, 0.40 metros. ¿Recordaste cómo convertir los centímetros en metros? Anota en la tabla ambos resultados
Pasa ahora a la división que sigue.

Tienes ahora 4 metros de listón y se cortarán en 5 partes iguales, vas a cortar el listón. Ya sabes que una posible estrategia es dividir todo el listón en tiras de un metro y luego, cada metro en cinco partes iguales, así que vas a cortar los cuatro metros y luego cada metro lo partes en quintos, es decir, en 5 partes iguales.
Realiza los cortes y deja sobre la mesa acomodados los cuatro metros uno debajo de otro y toma los primeros pedazos de cada fila, de estos quintos debes tomar 4, es decir, uno de cada metro. Se tiene un quinto, más un quinto, más un quinto, más un quinto.


¿Cuatro veces un quinto? Así es, se tienen los 4 quintos de todo el listón, falta saber cuánto miden esos tramos. Debes saber cuánto miden estos tramos que se obtuvieron. ¿Cómo se te ocurre que podrías hacerlo?
Una forma de expresar la medida de los cuatro quintos juntos, ya observaste que una quinta parte del metro mide 20 cm, entonces si estás considerando 4 quintas partes, serían 80 cm.

Esa es una muy buena estrategia para saber cuánto miden, pero ahora faltaría expresar esa longitud en metros no en centímetros. Como es de una unidad menor a una mayor, hay que dividir, entonces tendrías que dividir 80 entre 100 y eso te da 0.80 metros.
Anota en la tabla cuatro quintos igual a 0.80
Otra forma en que se podría obtener este resultado se logra al considerar que 4 metros son lo mismo que 400 centímetros, entonces podrías dividir 400 entre 5 y obtener la longitud de cada tramo, que sería 80 centímetros. Ya sólo faltaría hacer la misma conversión que hiciste antes para convertir la expresión de centímetros a metros, ese procedimiento sintetiza todo lo que se ha hecho hasta ahora y, convertidos a metros son 0.80 metros.
También podrías escribir que es igual a ocho décimos así es 0.80 es igual que 0.8 recuerda que se pueden eliminar los ceros a la derecha de los decimales, siempre y cuando no haya otra cifra diferente después de esos ceros.
Ahora pasa a la siguiente división.

Dice que son 6 metros de listón divididos en 5 partes. ¡Otra vez quintos! Así es, pero analiza y observa qué diferencia se encuentra. En los anteriores había sido menor el número de metros de listón que el número de partes en los que se pedía que se dividieran, ahora 6 es mayor que 5
Empieza por cortar las tiras de un metro y luego cada una en 5 partes iguales. Realiza los cortes y acomódalos uno detrás de otro para que quede el metro completo.
Pero considera, si fueran 5 metros divididos entre 5 partes, ¿Cuánto mediría cada parte? Cada parte sería de un metro. Sin embargo, ahora debes tener 6 quintas partes, ¿Qué podrías hacer?

Puedes separar los cinco metros y el metro extra, es decir, el sexto metro, lo puedes cortar en 5 partes y cada quinto de metro lo repartes con los anteriores. Así ya tendrías 6 quintos. Los 5 quintos que tiene cada metro más, este quinto que estas repartiendo con cada uno para que sean 6 quintos.
Entonces con 6 quintos se forma un metro más un quinto.

¿Cómo expresaría esta cantidad con números decimales? Ya observaste que un quinto de metro son 20 cm, entonces puedes sumar 6 veces 20 cm, lo que da 120 cm.
Estos 120 cm cómo se expresan en metros, nuevamente divide 120 entre 100 y te dará 1.20 metros. Recuerda que también puedes expresarlo como 1.2 m.
1.20 m = 1.2 m
Actividad 2
Realiza las operaciones siguientes.
Actividad 3
Revisa la situación siguiente en la que puede ayudar lo que hoy has estado estudiando.
Para hacer una actividad en artes, un alumno necesita elaborar cuatro figuras con plastilina, pero para hacerlas sólo tiene tres barras de plastilina de color azul iguales y quiere la misma cantidad de plastilina para cada figura y que no sobre nada, para que todas las figuras le queden del mismo tamaño.
¿Cuánta plastilina tiene que ocupar para cada figura?
Ve por partes, ¿Qué es lo que vas a dividir?
¿Tres barritas de plastilina azul? Tienes que repartir tres barritas iguales entre cuatro figuras que vas a hacer.
- Barras de plastilina → 3
- Número de figuras → 4
¿Te recuerda algo este problema? Sí, eso se parece a lo que se ha hecho con los listones.
Entonces, ¿Crees qué podrás resolverlo de manera semejante a las situaciones del listón? ¿Cómo? cortando cada barra de plastilina en 4 partes iguales.

Después tomas un cuarto de cada una parte para cada figura que vas a hacer, entonces, ¿Cuánto utilizarás para cada figura? En cada figura usarás tres cuartos de plastilina, que también equivale a tres veces un cuarto.
Para cada figura vas a ocupar 3 cuartos de plastilina, así las figuras quedarán del mismo tamaño, porque en las tres usarás la misma cantidad de plastilina.
¿Cómo podrías saber qué cantidad de plastilina se usaría para cada figura antes de cortarla o sin hacer dibujos?
Después de trabajar con los listones te diste cuenta de que puedes hacer la división de 3 entre 4 da, tres sobre 4 que lo puedes escribir como fracción, pero también como número decimal y sería, cero punto setenta y cinco.

Lo puedes escribir como 3 cuartos o como número decimal y serían 75 centésimos, puede ser más fácil como 3 cuartos, porque sería difícil cortar 75 centésimos de plastilina.
Efectivamente, en este caso, conviene usar la expresión en forma de fracción, 3 cuartos de cada barra de plastilina se ocupan para cada figura, es decir, menos de una barra.
El reto de hoy:
Comparte con alguien cercano, lo que aprendiste al respecto de las fracciones que se obtienen cuando son mayores o menores que el entero. Explícale con alguno de los ejercicios realizados.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
