Separamos el pedido
Separamos el pedido
Aprendizaje esperado: identificación de escrituras equivalentes (aditivas, mixtas) con fracciones. Comparación de fracciones en casos sencillos (con igual numerador o igual denominador).
Énfasis: usa diversas formas aditivas para representar una fracción mixta.
¿Qué vamos a aprender?
Aprenderás cómo descomponer un número mixto en una suma de varias fracciones menores, así como diferentes maneras de representar un número mixto con ayuda de otros números.
¿Qué hacemos?
Para iniciar te platico que, he notado que hay temporadas en las cuales diversas tiendas tienen promociones económicas que son interesantes, en ocasiones incluso las ofertas son muy atractivas.
Comúnmente estamos acostumbrados a observar ofertas que brindan descuentos, o igual te proponen que si compras cierta cantidad de productos te regalarán uno extra, pero deja te comento que en una ferretería cerca de mi casa hay una oferta que justamente tiene que ver con la temática que vas a trabajar el día de hoy. Sabes, ¿Qué tiene de interesante la oferta?
La oferta es la siguiente: En la tercera compra que se haga de cemento, hay un regalo, es decir, si haces 3 pedidos de cemento, en el tercero que hagas, ¿Te dan un regalo?
Y justo me platicaban que un señor necesitaba 6 kg de cemento, pero que cuando se enteró de la oferta decidió hacer su pedido en 3 partes.
Entonces lamentablemente repartió los seis kg y medio en tres pedidos y te preguntarás, ¿Por qué lamentablemente? Porque cuando llegó a su domicilio se percató de que había cometido un error y no realizó de forma adecuada el pedido, pues la cantidad que necesitaba de cemento no era la que necesitaba.
¿Sabes qué cantidad fue la que solicitó en cada pedido? Para ello requirió de números mixtos.
Sí, de números mixtos.
Recuerda que los números mixtos son aquellos que contienen una parte entera y una parte fraccionaria.
Por ejemplo, si colocas 1 entero y ¿Aquí estarías hablando de un número mixto? Porque el uno está representando la parte entera y la parte fraccionaría es un medio.
Qué te parece si observas una imagen en la cual debes identificar los números mixtos.
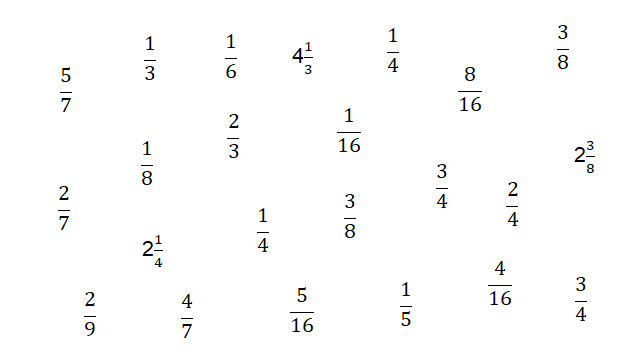
Puedes ver que en la imagen aparecen representadas varias cantidades, y el objetivo es que identifiques las que están representadas con un número mixto.
Pon mucha atención y veamos si encuentras algún número mixto entre todos ellos, concéntrate en buscar aquellos números fraccionarios que contengan una parte entera y una parte fraccionaria.
¿Ya encontraste la de 2?
Perfecto, entonces marca de rojo el número mixto encontrado.

Ahora, busquemos otro número mixto, ¿el? 4 Entonces, también márcalo con rojo y busca otro.
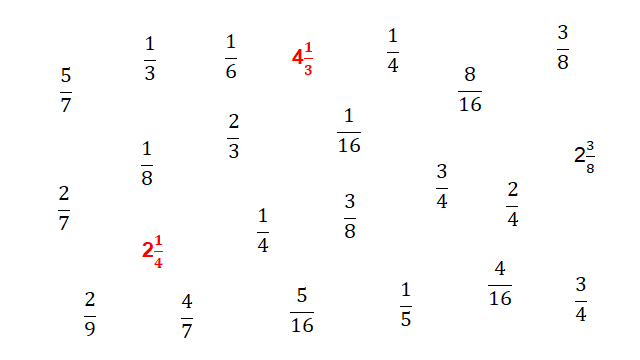
Encontraste el 2 Entonces hay que marcarlo igual con color rojo.
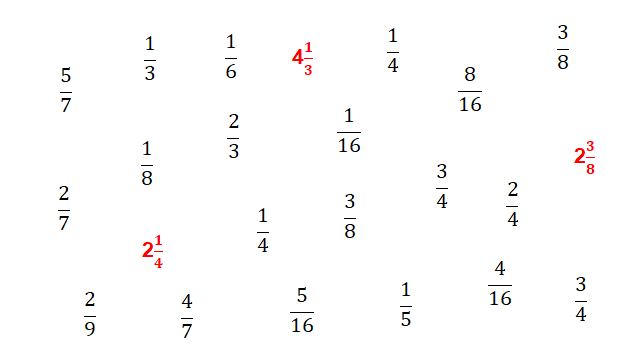
Entonces como ya tienes claro qué y cómo son los números mixtos, ¿Ya podrías decir cuáles son los tres pedidos de cemento que realizó el señor del que nos platicaba?
Cierto, el señor hizo los siguientes pedidos: El primero fue de 1, el segundo de 2 y el tercero de 1.
¿Alcanzas a ver el problema con los pedidos?
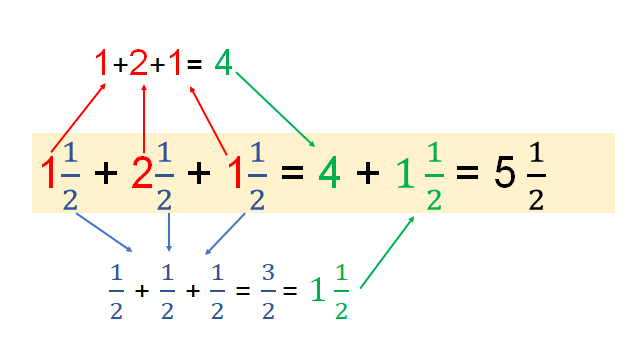
Si sumas los tres pedidos (1 + 2 +1 =) al realizar la suma tendrás que su resultado es tres medios. ( ahora suma los enteros y te da 4 enteros, en total son 4 enteros 3 medios (4) pero aún puedes convertir las fracciones en enteros, tienes tres medios, lo que es igual a un entero un medio.
Así que, al final en la suma de los tres pedidos da como resultado 5 enteros un medio (5 )
El señor realizó mal los tres pedidos, ya que el necesitaba seis kilogramos y medio, y una forma de cómo podría haber realizado su pedido para obtener la cantidad deseada, era que agregar un kilogramo más por lo que el pedido podría haber sido de un kilogramo y medio, otro de dos kilogramos y medio, otro más de dos kilogramos y medio, y todo eso junto da como resultado seis kilogramos y medio, que era la cantidad de cemento que el señor necesitaba.
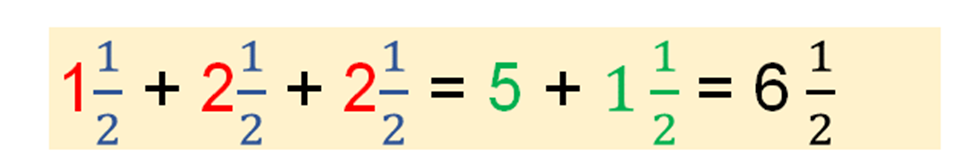
Entonces, qué opinas si ahora juegas a descomponer pedidos hechos a una ferretería, en otros tres más pequeños, así trabajas con números mixtos.
Aquí te dice artículo: Clavos pedido grande 5 kg entonces tienes que repartir el pedido grande en 3 más pequeños. ¿Qué te parece si inicias con un primer pedido de 2 kg?
El segundo pedido puede ser de dos kilogramos y un octavo (2 kg)
Ahora veamos cuánto llevas, si tienes el primer pedido de 2 kilogramos y el segundo de 2 kilogramos y un octavo; puedes sumar las dos cantidades y así saber cuánto llevas (2 + 2 = 4) muy bien, cuentas con cuatro kilogramos y tres octavos más un octavo son cuatro octavos, entonces llevas en total 4 kilogramos con cuatro octavos, y si el objetivo es cinco kilogramos con cuatro octavos tu tercer pedido sería de un kilogramo (+ 1 kg.)
Con eso completas la primera tarjeta, ahora observa en la imagen, otras formas de resolver este desafío.
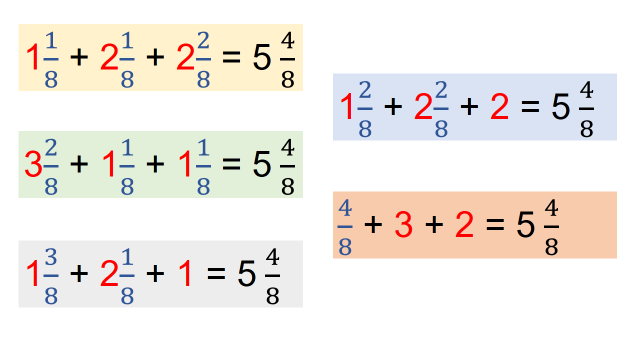
Observas que son muchas formas de resolver este desafío, hay muchas maneras de representar un número mixto con ayuda de otros números.
Ahora, estás listo para resolver los siguientes desafíos:
- Artículo: Cable telefónico. Pedido grande 9 m.
- Artículo: Lazo para tender. Pedido grande 7 kg.
- Artículo: Cáñamo. Pedido grande 8 m.
- Artículo: Tornillos medianos pedido grande 6 kg.
Recuerda las consignas que realizaste antes en tu libro de desafíos en la página 111
https://libros.conaliteg.gob.mx/20/P3DMA.htm

https://libros.conaliteg.gob.mx/20/P3DMA.htm?#page/111
Ese en que tenías varios recipientes y tenías que completar con ayuda de ellos un tamaño específico.
Ahora, qué opinas si repasas la actividad, resolviéndola nuevamente, pero ahora imagina que contarás con frascos con otras cantidades, de un cuarto, un medio, un litro y un litro y medio.
La consigna es: Coloca en el recipiente 2 litros, imagina que comienzas a vaciar un recipiente de 1 litros y a este también le agregas una de medio litro, por lo que llevas 2 litros y como ya sólo faltan tres cuartos de litro entonces, puedes vaciar tres recipientes de un cuarto y con eso ya completas la cantidad solicitada.
Esta actividad refuerza tu conocimiento de la manera cómo descomponer un número mixto en una suma de varias fracciones menores, justo como la primera actividad que realizaste.
Para continuar con tu aprendizaje, puedes jugar con tus familiares memorama de fracciones mixtas, tú puedes hacer tus propias tarjetas (10 tarjetas tamaño media carta).
Son 5 pares de tarjetas, en los cuales cada tarjeta contiene una suma de fracciones y, la tarjeta par solo es una fracción Mixta.
Ejemplo:
| 3 |
| 1 |
| 2 |
| 3 |
Tienes que buscar por un lado una tarjeta con una suma de fracción y la otra es el resultado en fracción mixta. Esperamos que te diviertas.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas
