Repartiendo problemas
Repartiendo problemas
Aprendizaje esperado: resolución de problemas particulares en tercios, quintos y sextos. Análisis de escrituras aditivas equivalentes y de fracciones mayores o menores que la unidad.
Énfasis: resolver problemas de reparto que implican usar y comparar fracciones (medios, cuartos, octavos; tercios, sextos, quintos, décimos).
¿Qué vamos a aprender?
Fortalecerás los conocimientos para resolver problemas con fracciones.
¿Qué hacemos?
Recordarás que, si divides un objeto o unidad en varias partes iguales, a cada una de ellas, se les denomina fracción.
Las fracciones están formadas por dos números: el numerador y el denominador.
El denominador indica el número total de partes iguales en que se divide la unidad.
El numerador indica las partes iguales que tomamos en cuenta del total en que dividimos el entero o unidad.
Ilustremos estos conceptos:
Observa el siguiente ejemplo: La mamá de Norberto elaboró una gelatina.

La repartió entre los 8 asistentes.
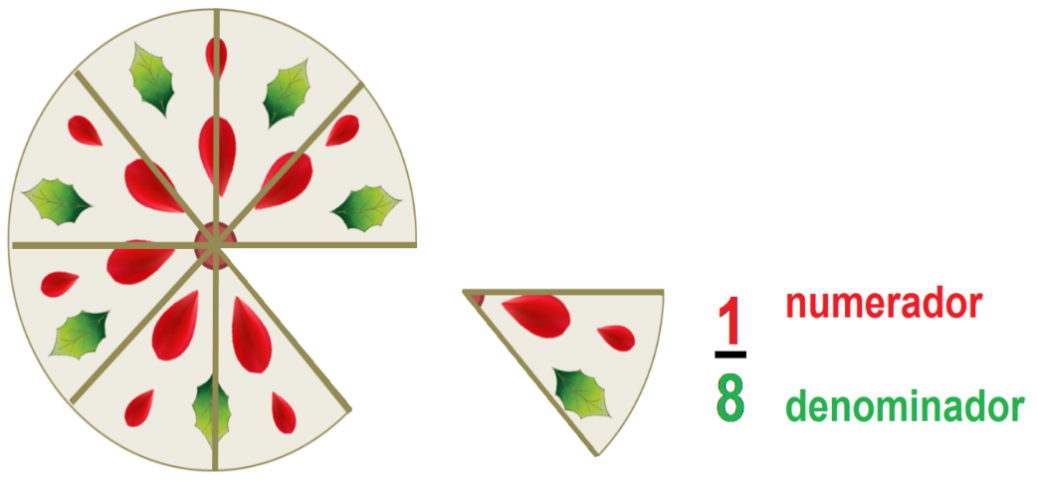
Apliquemos estos conceptos en las siguientes figuras, que ya se encuentran divididas, lo que harás en estos círculos será iluminar la parte que se indica en la fracción.
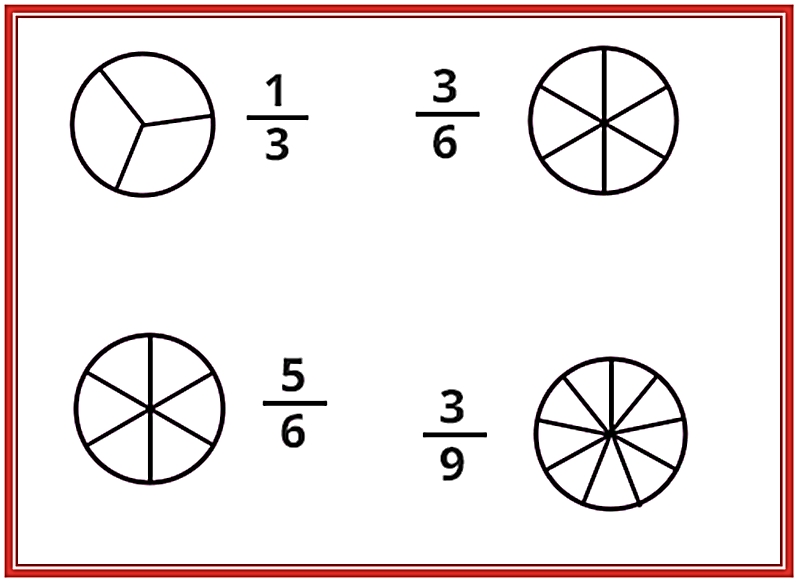
Atendiendo a lo que se indica, tendrías en cada círculo pintadas las siguientes partes:
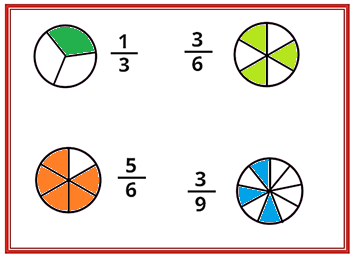
Estas fracciones indican tercios, sextos y novenos, es muy importante que recuerden que para su correcta lectura primero se pronuncia el numerador seguido del denominador por lo que la lectura correcta sería “un tercio, tres sextos, cincos sextos y tres novenos”.
Ahora trabajarás con fracciones que ya conoces, entre aquellas que tienen como denominador números que se obtienen multiplicando el 2 por un número determinado de veces y que se representa gráficamente al partir en mitades (mitad de une entero es un medio, la mitad de un medio es un cuarto, la mitad de un cuarto es un octavo, etcétera). También revisarás algunos números que son múltiplos de 3, esto es 6 o 9 por el momento.
Para esta actividad debes identificar cual es la información faltante y anotarla en el espacio que corresponde, para ello debes analizar en cada caso la parte que esta iluminada.
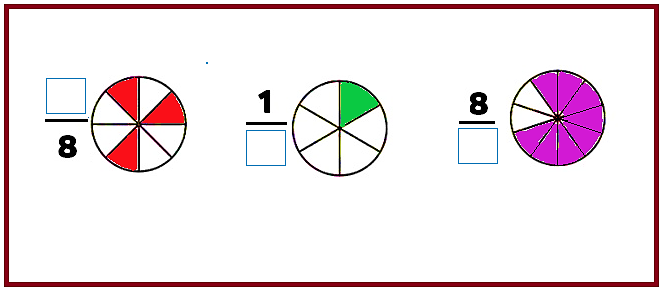
Como puedes observar, en el primer círculo debes indicar las partes que han sido pintadas, es decir, el numerador, en el segundo círculo debes indicar el denominador, es decir, en cuántas partes ha sido dividido el entero y en la tercera figura también debes indicar el denominador.
Así los números que indican la información correcta son:
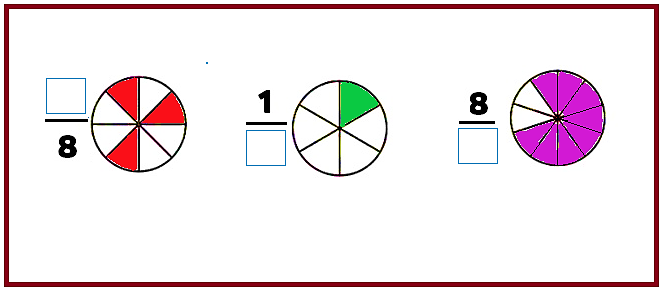
Así los números que indican la información correcta son:
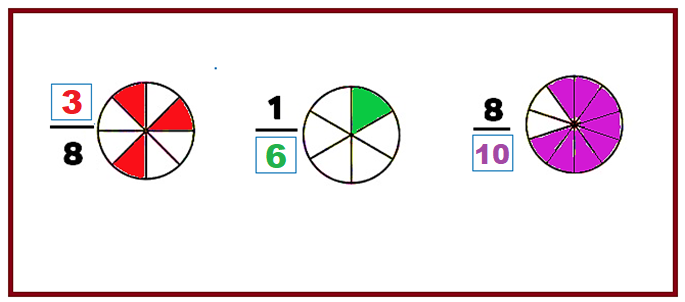
“Tres octavos”, “un sexto” y “ocho décimos”.
Ahora, si tienes las siguientes fracciones, ¿Cuál de las dos fracciones es mayor?
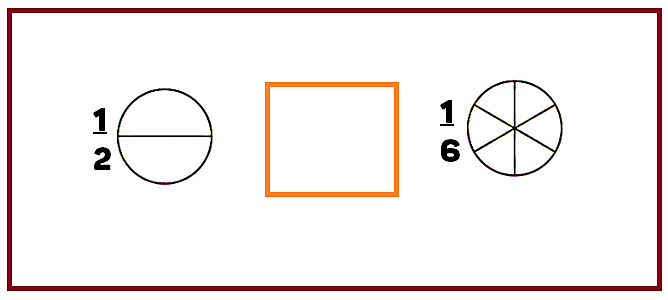
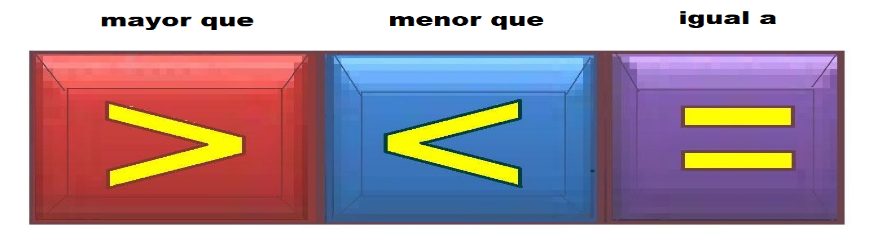
Recuerda que, para indicar estas relaciones de valor, utilizarás los símbolos Mayor que, Menor que e Igual.
Es importante recordar que un procedimiento que te puede ayudar a comprender mejor las relaciones de valor entre las fracciones es indicarlas de alguna forma en este caso pintando la parte indicada, así podemos observar que un medio es mayor que un sexto.
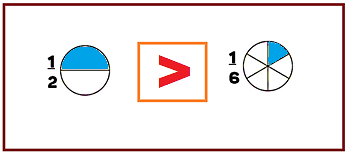
Compara otro par de fracciones.
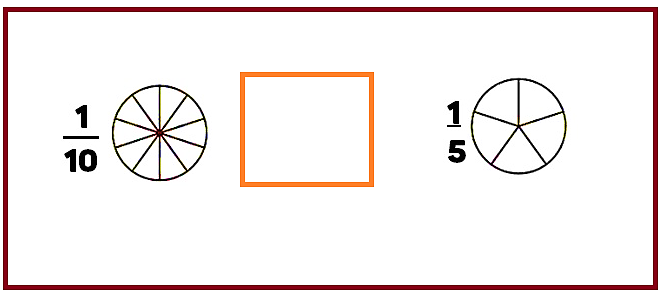
Después de iluminar las fracciones correspondientes, observa que un décimo es menor que un quinto.

Vas a iluminar la fracción que se indica en cada caso, y finalmente vas a decir cuál es menor. Las fracciones son:
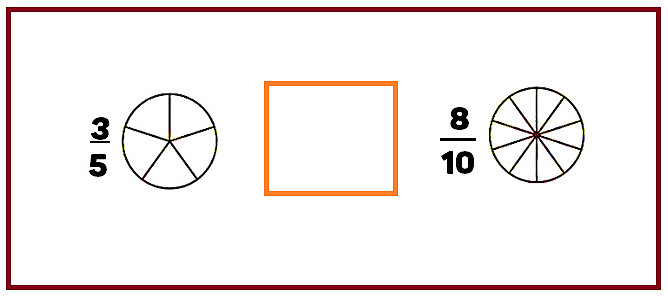
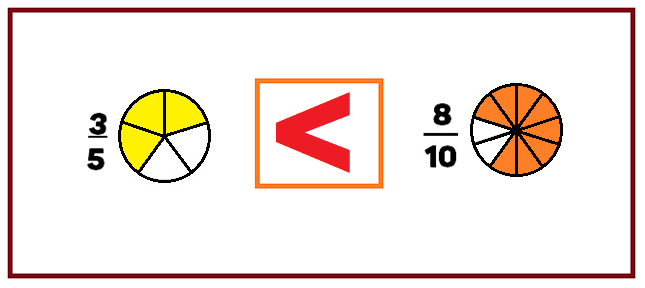
Después de iluminar las fracciones correspondientes, observa que tres quintos es menor que ocho décimos.
La siguiente actividad consiste en armar un memorama en el que debes relacionar 4 representaciones gráficas de fracciones con sus respectivas representaciones numéricas.
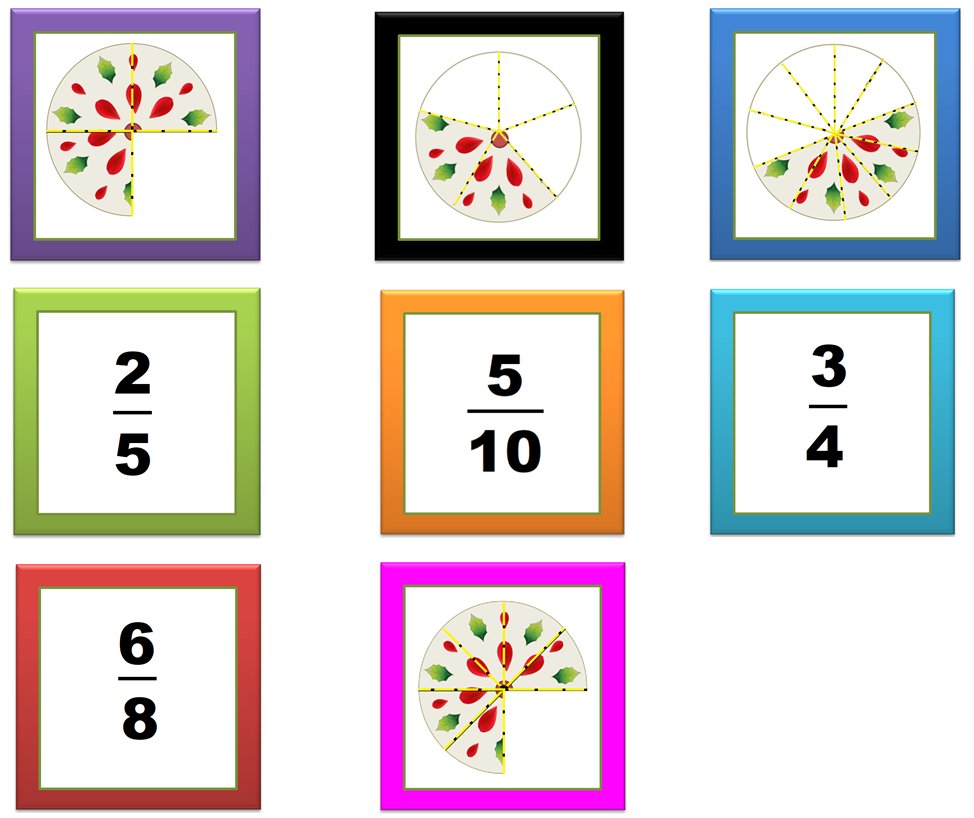
Tienes 8 tarjetas que debes recortar y colocar hacia abajo sobre una mesa por turno, (puedes invitar a un familiar) voltearás dos tarjetas, si ambas coinciden en representar la misma cantidad, las colocaras juntas, te anotarás un punto y tendrás el derecho de volver a sacar otro par; de no coincidir, las dejaras en su lugar hacia abajo y le tocará el turno al oponente. El juego termina cuando hayas asociado todos los pares correctamente.
Para finalizar, plantearás dos problemas, ve al primero.
En una reunión repartieron una gelatina. A Gabriel le dieron 2/6 de gelatina y a Ana 3/8 ¿A quién le dieron una porción mayor?, ¿Cómo puedes encontrar la respuesta correcta?

Puedes determinar una respuesta sobre poniendo las partes de gelatina.
Angélica preparó un pay que dividió en ocho partes, si su familia está formada por seis integrantes incluida ella, y cada uno comió una rebanada, ¿Qué parte del pay le tocó a cada uno?
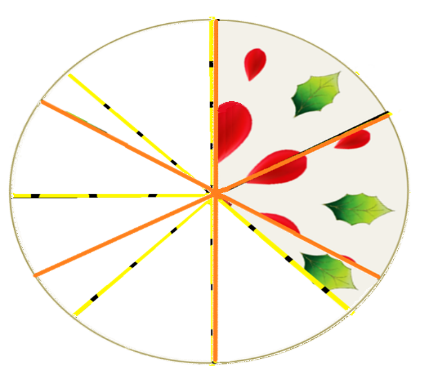
Como puedes apreciar en la imagen al sobreponer ambas fracciones 2/6 es menor que 3/8.
Debes tener presente que para utilizarla sobre la posición como un recurso de comparación entre fracciones nuestros enteros deben ser del mismo tamaño y las fracciones deben estar marcadas sobre el entero de forma pertinente.
Así que, respondiendo la pregunta; le dieron una mayor porción de gelatina a Ana.
Ve al último problema.

A cada uno le tocó 1/8 ya que lo que repartimos fue el pay que Angélica dividió en ocho partes.
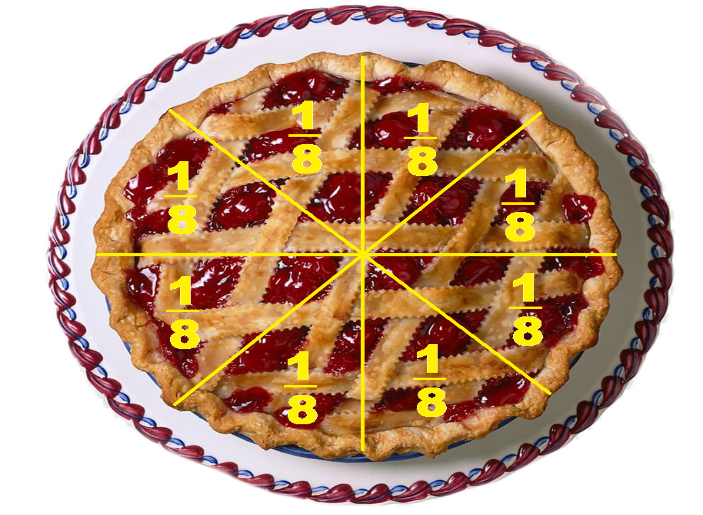
Así es, la respuesta es 1/8, este es un ejemplo de problemas que tienen datos de más, como el número de integrantes de la familia, por lo que es importante reflexionar sobre el tipo de información que la redacción nos proporciona y cómo esta información está relacionada con la pregunta planteada o entre sí.
Sin duda una reflexión muy importante.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
