Relación perímetro-área
Relación perímetro-área
Aprendizaje esperado: calcula aproximadamente el perímetro y el área de figuras poligonales mediante diversos procedimientos, como reticulados, yuxtaponiendo los lados sobre una recta numérica, etcétera.
Énfasis: distingue el perímetro y el área de figuras poligonales, mediante el trazo de polígonos que tengan la misma área y diferentes perímetros, igual perímetro y diferentes áreas, e igual perímetro y área.
¿Qué vamos a aprender?
Continuarás trabajando con el perímetro y el área de diferentes polígonos.
¿Qué hacemos?
Recuerda que, un polígono es una figura geométrica plana formada por varios segmentos de recta que delimitan una superficie.
En la imagen puedes observar algunas figuras que conoces, como un triángulo, un pentágono y un rectángulo. ¿Identificas las otras dos?
En la imagen hay figuras regulares y figuras irregulares, que son las que no tienen sus lados ni sus ángulos iguales, pero como puedes observar, todas están formadas por segmentos de recta, que son los que forman el perímetro de cada figura y que delimitan su área.
Observa la siguiente cápsula, para que comprendas un poco más los términos de perímetro y área.
- Cápsula de Don Leopoldo y Cupertino.
(del min. 3.50 al 9.08)
Ese es el tema que estudiarás este día, comenzarás por analizar lo siguiente:
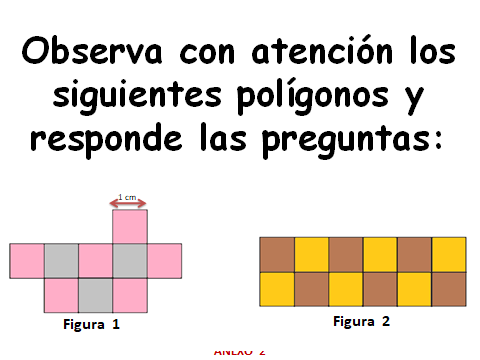
Recuerda que ya has usado unidades cuadradas para formar las figuras, pero hasta ahora no se ha determinado una medida para esa unidad, así que, se establecerá que la primera unidad de medida tiene un centímetro por cada lado. Observa con atención los siguientes polígonos y responde las preguntas.
Analiza con atención cada una de las imágenes que se muestran a continuación y trata de responder las preguntas ahí planteadas.
Debes contar cada una de las líneas de un centímetro que rodean la figura. ¿Ya terminaste de contar?
En ambas figuras el perímetro mide 16 centímetros.
Figura 1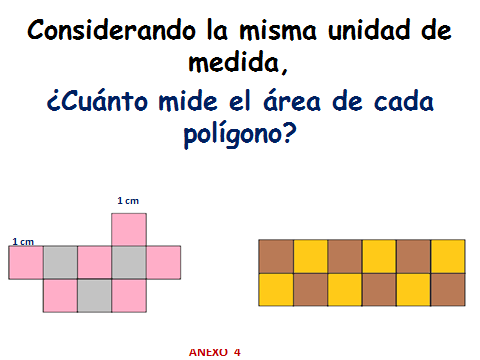
Figura 2
¿Cuál es la respuesta?
La figura 1 mide 9 centímetros cuadrados y la figura 2, 12 centímetros cuadrados.
Como recordarás, ayer también mediste el perímetro y área de estas figuras y obtuvimos la misma cantidad, lo que cambia es la unidad que acompaña a nuestra respuesta. Ayer no tenías establecida la medida de la unidad con la que las mediste, se dijo que serían centímetros, por lo tanto, tú respuesta tiene que ir acompañada de centímetros para el perímetro y centímetros cuadrados para el área.
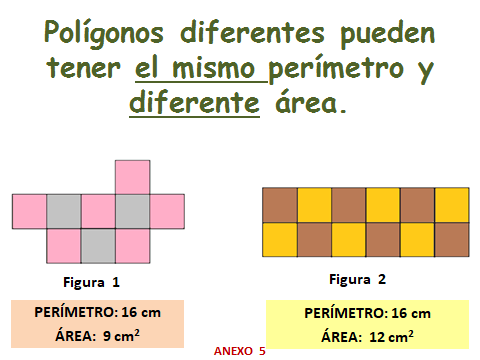
Nuevamente se concluye que puede haber figura con igual perímetro, pero diferente área.
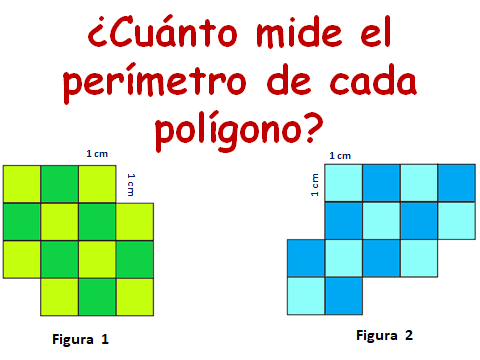
Observa la siguiente imagen, y contesta la pregunta. ¿Cuánto mide el perímetro de cada polígono?
En este caso, de nuevo puedes contar y eso te facilitará dar una respuesta. Con la cuadrícula se facilita responder cuanto mide el perímetro y el área de cada uno de estos polígonos.
De la figura 1 son 16 centímetros y de la figura 2 son 18 centímetros.
O lo que es lo mismo, en este caso, ¿Cuántos centímetros cuadrados mide cada figura? Porque estas observando que la unidad de medida es un cuadrado que mide un centímetro por lado.
La figura 1 mide 14 centímetros cuadrados y la figura 2 también mide 14 centímetros cuadrados.
Por lo tanto, ahora también se podría decir que dos polígonos diferentes pueden tener la misma área y diferente perímetro.
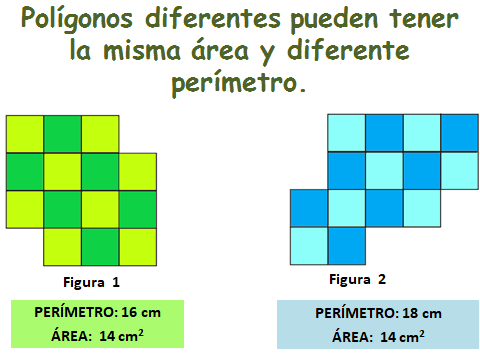
Ambas figuras tienen la misma área, pero diferente perímetro.
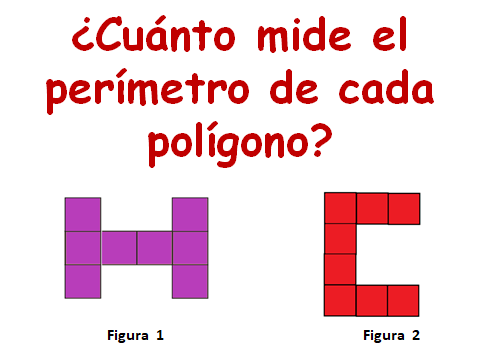
La figura 1 mide 18 unidades y la figura 2 también mide 18 unidades. Ambas tienen el mismo perímetro.
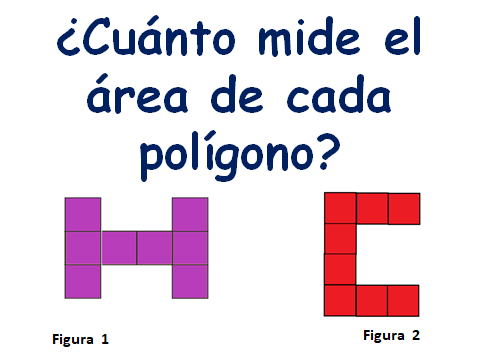
Las áreas de las dos figuras miden 8 centímetros cuadrados.
Entonces se establece que, puede haber figuras diferentes con el mismo perímetro y la misma área.
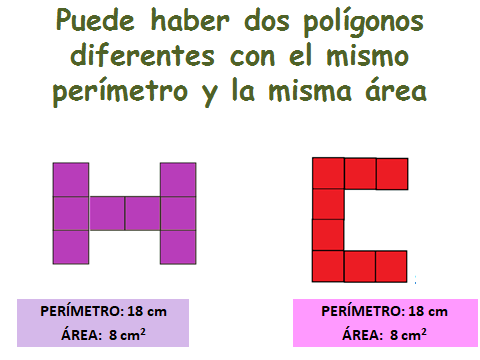
Los dos polígonos, aunque son diferentes, tienen la misma área y el mismo perímetro.
Para que continúes con el trabajo de áreas y perímetros, responde las siguientes preguntas.
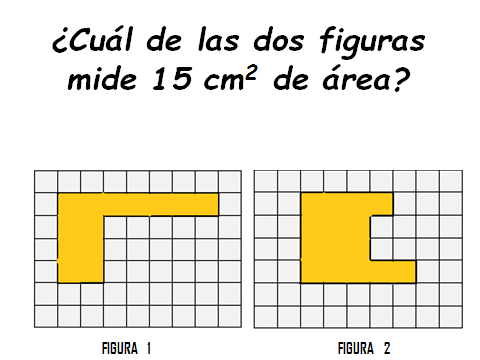
¿Ya tienes la respuesta?
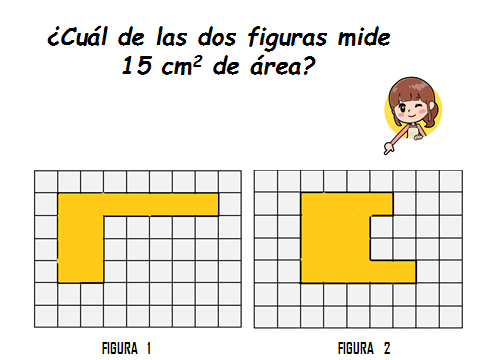
La figura 2 mide 15 centímetros cuadrados y la figura 1 mide 22 centímetro cuadrado.
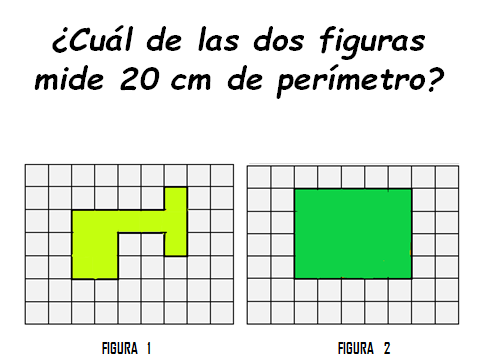
Cuenta bien para que respondas acertadamente.
La figura 1 mide 20 centímetros de perímetro, la figura 2 mide 18.
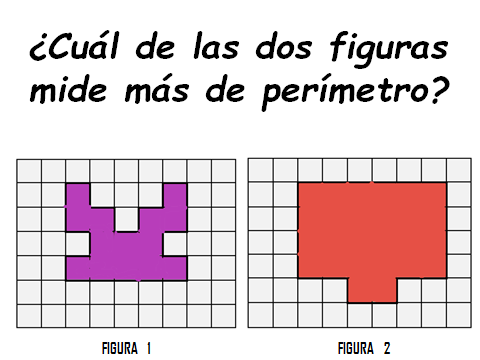
Analiza y cuenta detenidamente, para que tú respuesta sea correcta.
La figura 1 mide 26 centímetros de perímetro y la figura 2 mide 22 centímetros, por lo tanto, la respuesta correcta es la figura 1, es la de mayor perímetro.
Analiza bien cada una de las figuras y responde.
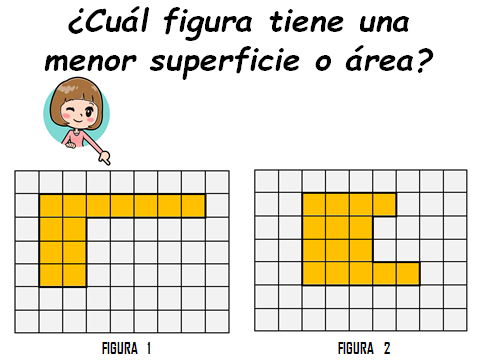
La figura 1 porque mide 13 centímetros cuadrados, mientras que la figura 2 mide más, o sea 15 centímetros cuadrados.
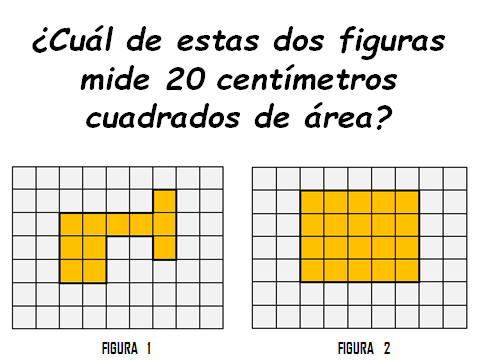
¿Ya lo tienes?
La figura 2 es la que mide 20 centímetros cuadrados.
¿Ya tienes más clara la diferencia entre perímetro y área?
Aunque quizá sea muy notorio que es la figura 2 debes contar cada centímetro cuadrado para estar seguro y evites equivocarte en la respuesta.
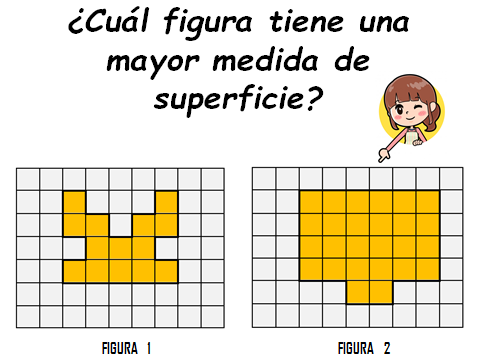
La respuesta es: la figura 2 con 26 centímetros cuadrados, porque la figura 1 tiene sólo 14 centímetros cuadrados de superficie.
Para finalizar, realiza el siguiente ejercicio, y para ello, observa con atención la siguiente imagen:
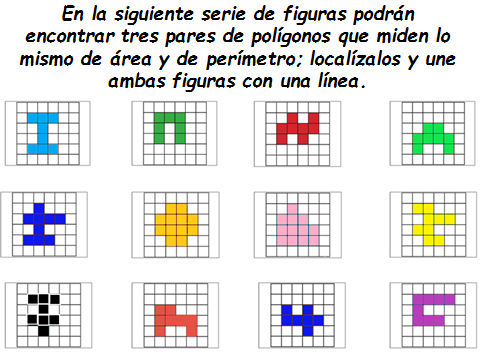
Quiere decir que, de las doce figuras que observas en la imagen, hay tres pares que coinciden tanto en la medida de su área como de su perímetro.
El primer par de polígonos que tienen la misma medida tanto en su perímetro como en su área, son:
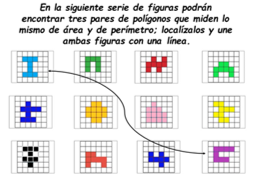
Ambas figuras miden 8 unidades cuadradas de área y 14 unidades de perímetro.
Observa con mucha atención los demás polígonos e identifica los otros dos pares que miden lo mismo de área y de perímetro.
x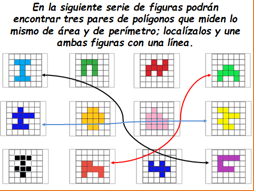
Las figuras que están con marcador rojo miden 16 unidades de perímetro y 8 unidades cuadradas de área. Y las de marcador azul, 20 de perímetro y 9 de área.
Fuente: https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/151
Con lo que observaste este día, te será más fácil resolver el desafío 81, de las páginas 151, 152 y 153 de tú libro de Desafíos Matemáticos.
Has vencido el reto de encontrar relaciones entre perímetro y área en diferentes figuras.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas