¿Qué parte le toca a cada uno?
¿Qué parte le toca a cada uno?
Aprendizaje esperado: resuelve problemas que impliquen una división de número fraccionario o decimal entre un número natural.
Énfasis: encuentra un procedimiento para dividir una fracción entre un número natural, cuando el numerador de la fracción es múltiplo del natural.
¿Qué vamos a aprender?
Resolverás problemas que impliquen una división de número fraccionario o decimal entre un número natural, así también deberás encontrar un procedimiento para dividir una fracción entre un número natural, cuando el numerador de la fracción es múltiplo del natural.
¿Qué hacemos?
Trabajarás con situaciones que implican operar con fracciones, parte del problema siguiente. Una persona debe ir a la ciudad de Pachuca a la casa de su mamá. Viaja para suministrar jabón y gel antibacterial entre los dispersores de su casa y los de la casa de su mamá en partes iguales, como medida para evitar el contagio de COVID 19
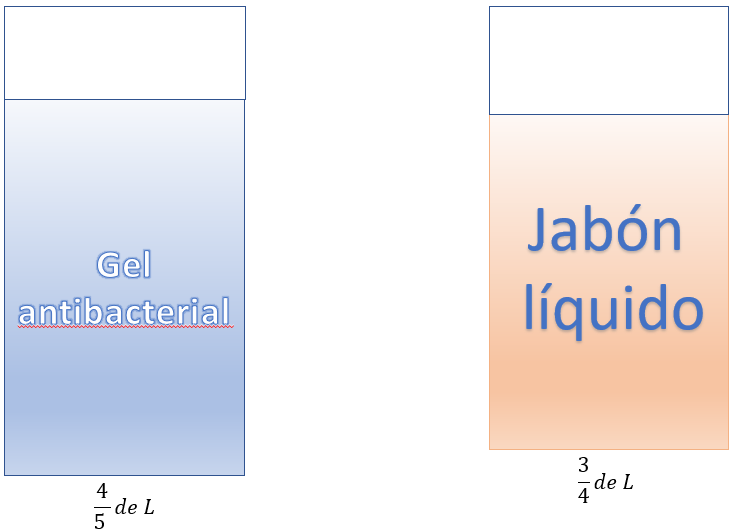
Tiene una botella con tres cuartos de litro de jabón líquido y una botella con cuatro quintos de litro de gel antibacterial. El jabón lo debe repartir en tres dispensadores de jabón iguales y el gel en ocho envases pequeños iguales que utiliza cada uno de los integrantes de su familia.
Para resolver este problema empieza por anotar las cantidades de gel antibacterial y jabón líquido que tienes, de jabón tienes tres cuartos de litro y lo debes repartir en tres dispensadores, entonces a cada dispensador le corresponde la tercera parte de tres cuartos y eso es, pues una división, esa operación la puedes representar gráficamente de la siguiente manera:
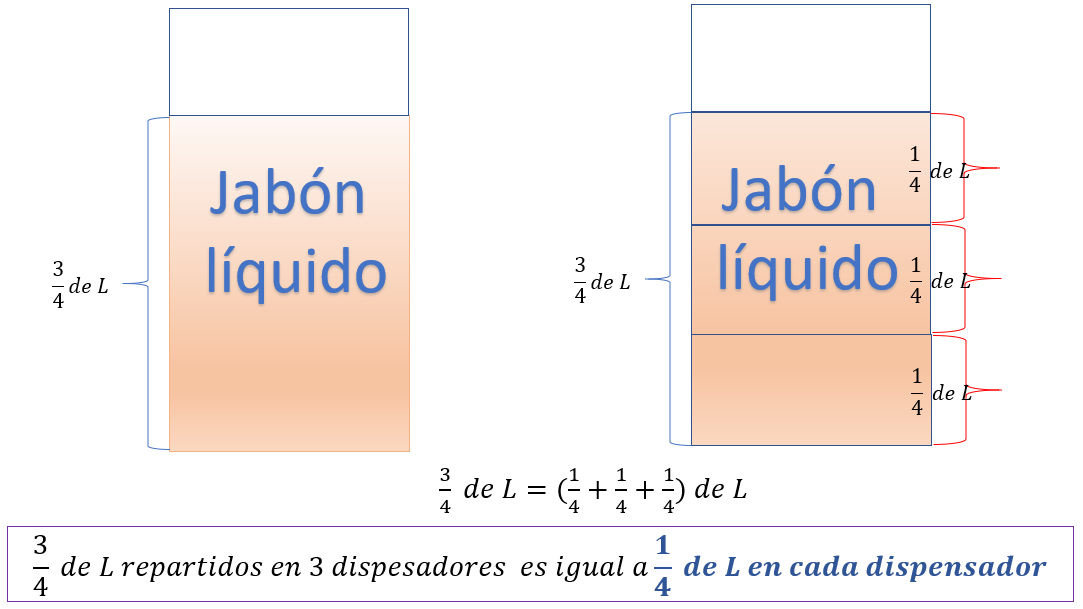
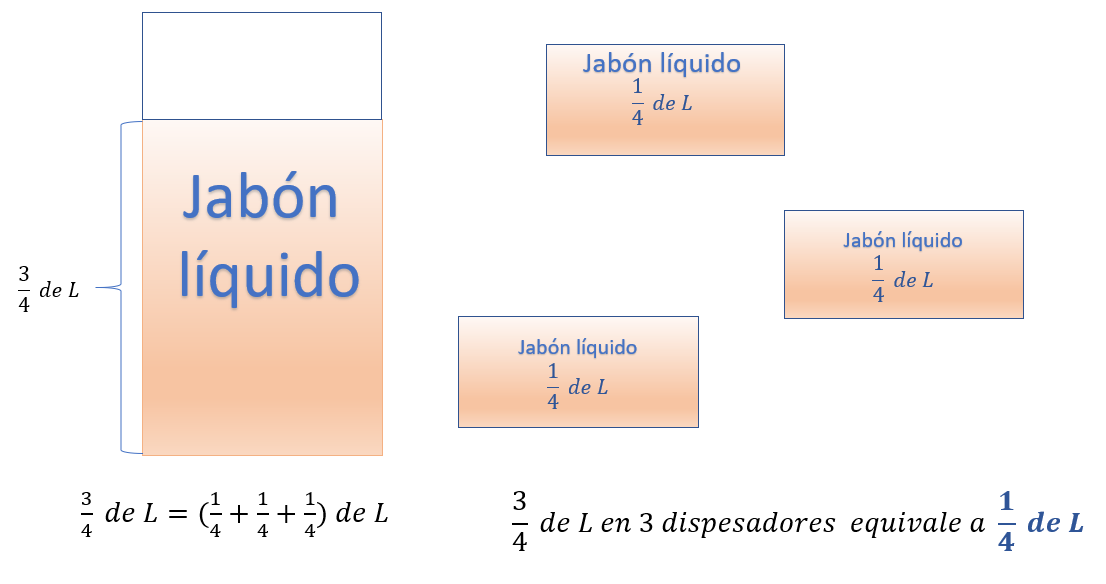
Tres cuartos de litro de jabón líquido, equivale a la suma de un cuarto más un cuarto más un cuarto, lo que permite reconocer que la tercera parte de tres cuartos de litro de jabón equivale a un cuarto, entonces repartir tres cuartos de litro de jabón en tres envases, significa que cada envase tiene un cuarto de litro de jabón líquido.
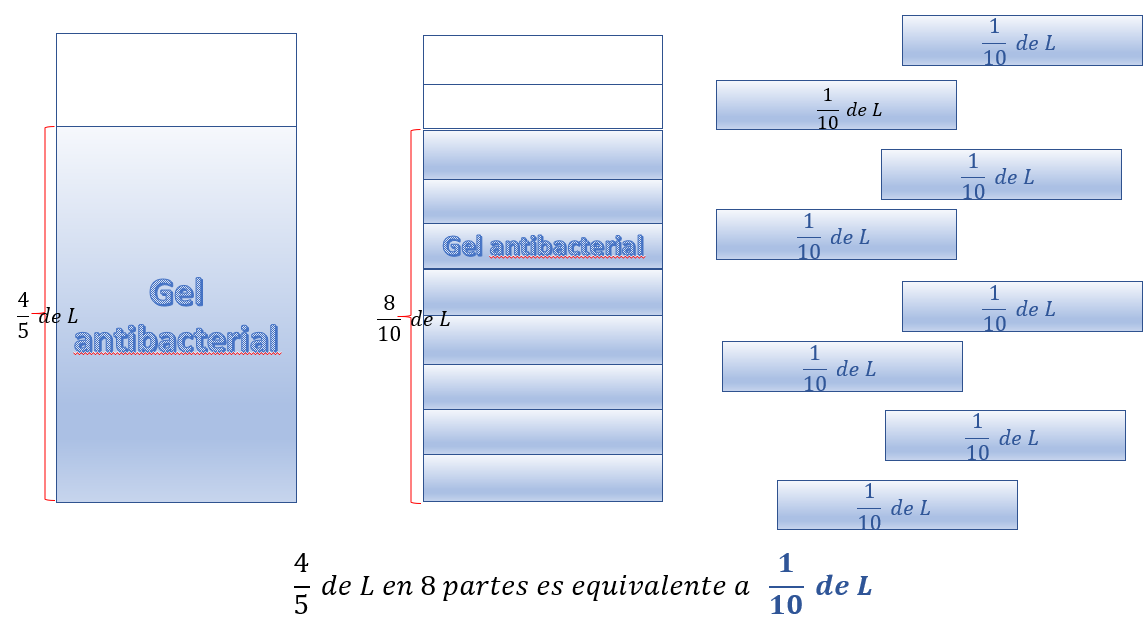
Observa cómo repartir la cantidad de gel antibacterial, es el mismo proceso en lo general, primero, considera la representación gráfica de la situación: cuatro quintos de litro de gel antibacterial será repartido en 8 envases pequeños iguales.

Cada uno de los integrantes de esta familia tiene su propio envase que carga a todos lados a donde vaya. Observa que cuatro quintos de litro de gel es equivalente a ocho décimos de litro de gel. Los ocho décimos se puede expresar como la suma de ocho veces un décimo, lo cual permite observar que repartir ocho décimos entre ocho es igual a un décimo, siendo equivalente también a cuatro quintos entre ocho es un décimo, cada uno de los tres dispensadores de jabón líquido contiene un cuarto de litro, mientras que cada uno de los 8 envases pequeños de gel antibacterial contienen un décimo de litro de gel.


Ahora observa el video siguiente que presenta la manera de elaborar gel antibacterial de manera casera. Toma nota y comparte con tus familiares el procedimiento y los ingredientes que se requieren para hacerlo en casa, de no poder adquirirlo.

- Video. Gel antibacterial. Revista del Consumidor.
https://www.youtube.com/watch?v=OrR_qkrGRlg
La elaboración del gel antibacterial es sencilla, una vez que se cuenta con todos los ingredientes. No obstante, se recomienda la supervisión y participación de un adulto al momento de su elaboración, eso es importante para no ponerte en riesgo.
Ahora abre tu libro de desafíos matemáticos en la página 145 desafío número 79
https://libros.conaliteg.gob.mx/P6DMA.htm?#page/145

La consigna dice lo siguiente:

¿Tienes alguna propuesta para dar respuesta a la pregunta del problema que acabas de leer? Para comenzar es conveniente representar gráficamente la situación.

La figura completa representa el total de alumnos que hay en el grupo. El problema indica que cuatro sextos del total de alumnos del grupo van a participar en el concurso de danza. Cuatro sextos del grupo se pueden expresar como la suma de un sexto cuatro veces o la suma de dos sextos dos veces.
Ambas expresiones son equivalentes para representar cuatro sextos del grupo y desarrollarlas de esa manera permiten reagrupar o repartir, de acuerdo con las indicaciones que te dan en el problema, por ejemplo, ¿De qué manera representas la mitad de los alumnos que participan en el concurso de danza folclórica?
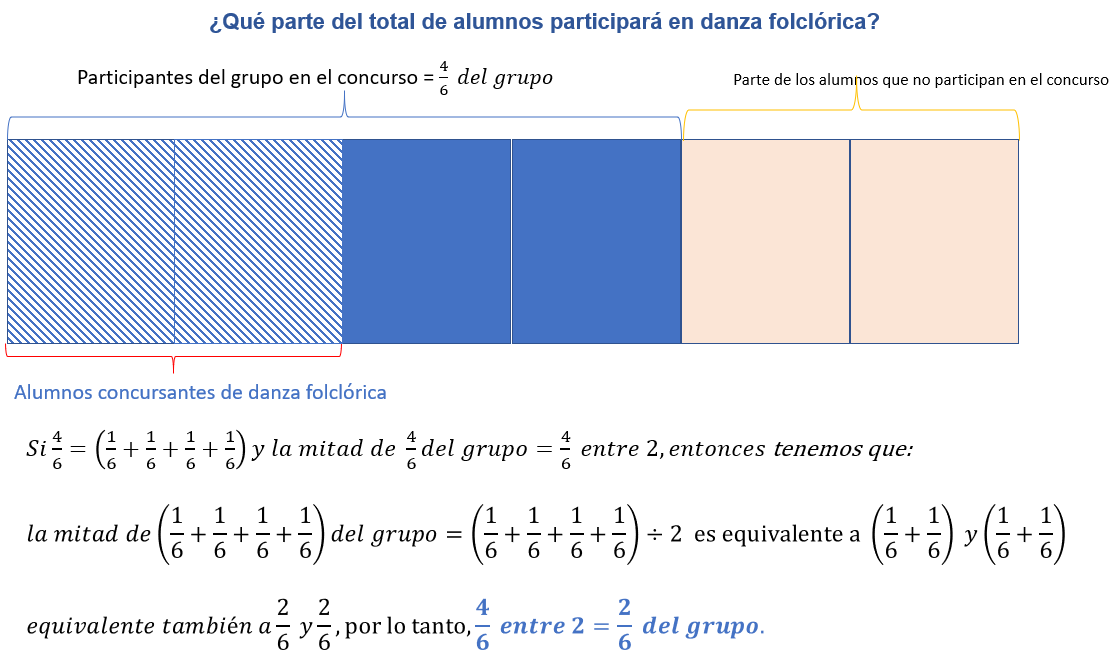
Los cuatro sextos de alumnos que participan en el concurso se dividen en dos grupos iguales, una mitad participa en danza folclórica y la otra mitad en danza clásica. Si representas primero a la mitad que participa en danza folclórica, una manera de hacerlo, considerando la suma de cuatro veces un sexto, es: tomar la mitad de la suma, esto es, dos veces un sexto que es igual a dos sextos, esa es una manera en que puedes determinar qué parte del total es la mitad de cuatro sextos.
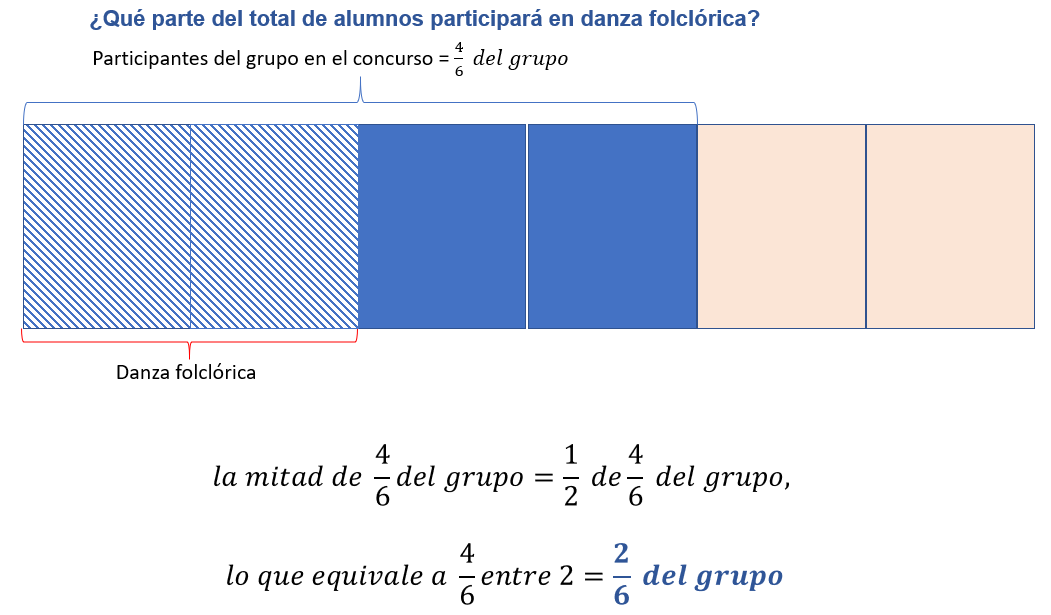
Si observas, en general, cuando te refieres a la mitad de algo puedes considerar que formas dos partes o conjuntos iguales. En este caso, la mitad de cuatro sextos es dos sextos como también lo puedes observar gráficamente y, recordando el trabajo que realizaste en clases anteriores, lo puedes expresar como una parte de una cantidad, en este caso, es un medio de cuatro sextos, también así puedes determinar qué parte del total de alumnos participa en la danza folclórica y obtienes que son dos sextas partes del grupo.
Ahora, para determinar qué parte del total de alumnos participa en la danza clásica considera que cuatro sextos es equivalente a dos tercios
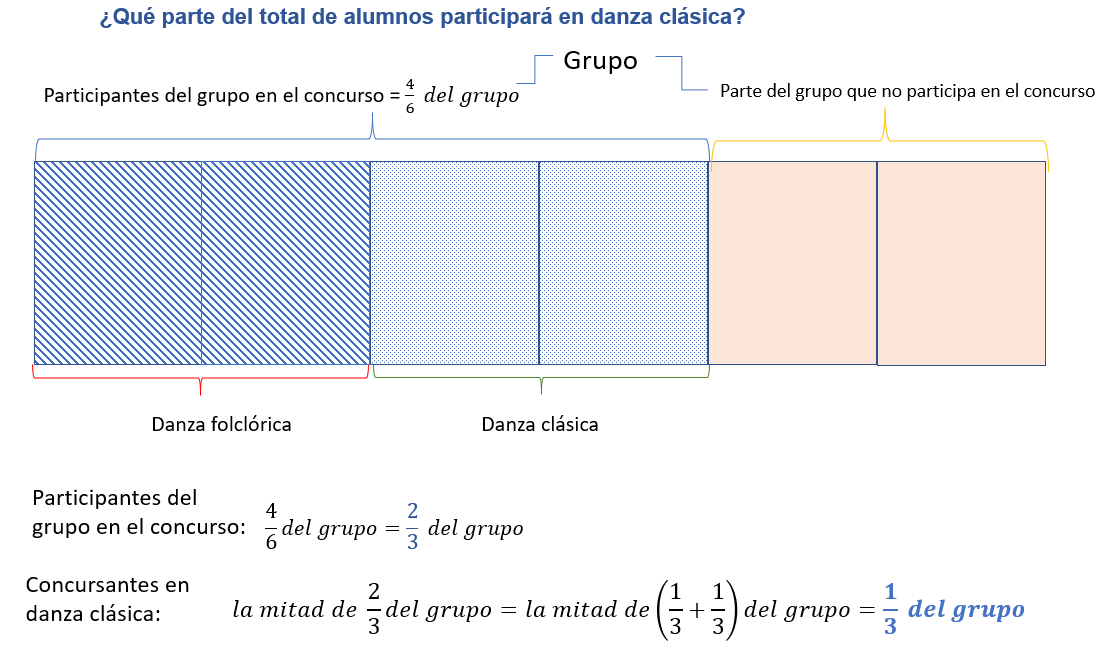
Entonces, dos tercios se puede expresar como la suma de dos veces un tercio, de ahí puedes considerar que la mitad de dos tercios es un tercio, como también se puede apreciar en la representación gráfica. En la representación gráfica de la situación se observa claramente que cuatro sextos es equivalente a dos tercios y, por otra parte, que la mitad de dos tercios es un tercio.

Observa que la respuesta la puedes expresar en tercios o en sextos, además, puedes observar que existe más de un procedimiento para dar respuesta a la pregunta, ¿Qué parte del total de alumnos participará en cada una de las dos piezas de danza?
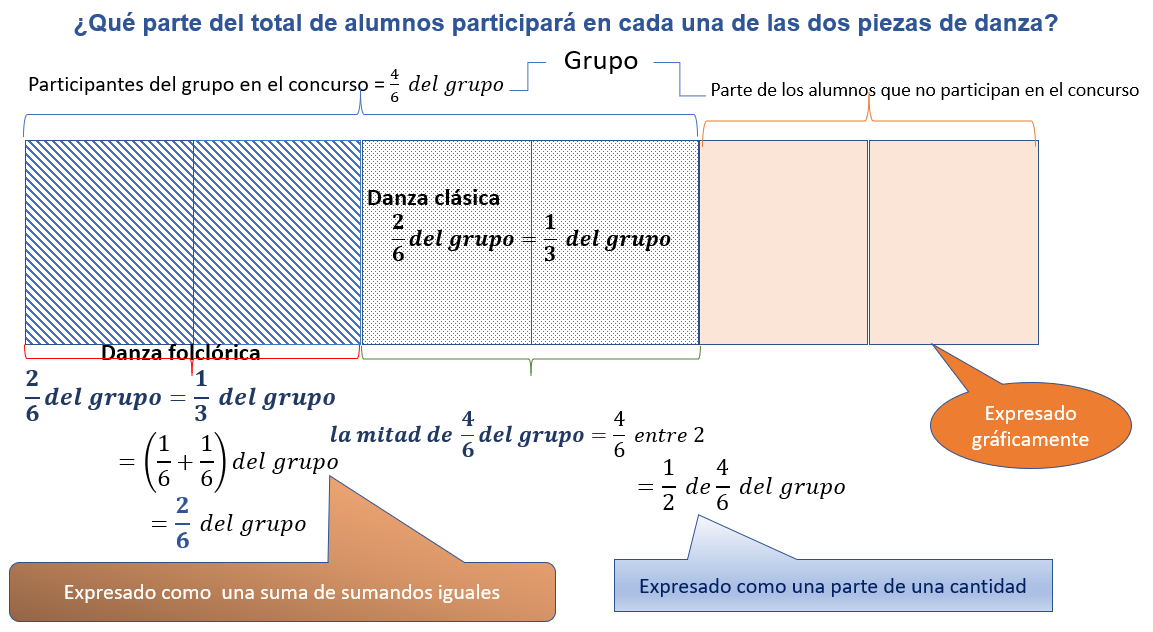
Por ejemplo, puedes resolverlo gráficamente, y además de la estrategia de expresar como suma de sumandos iguales, también la puedes interpretar como parte de una cantidad. Lo importante es interpretar y representar la situación correctamente, tanto gráfica como numéricamente. En este caso te apoyaste en la representación gráfica para poder encontrar alguna representación numérica.
Ahora observa que plantea la siguiente situación del desafío setenta y nueve.

Toma un tiempo para resolverlo, puedes utilizar alguno de los procedimientos utilizados en la situación anterior, pero toma en cuenta que el valor de las fracciones que están implicadas en esta nueva situación.
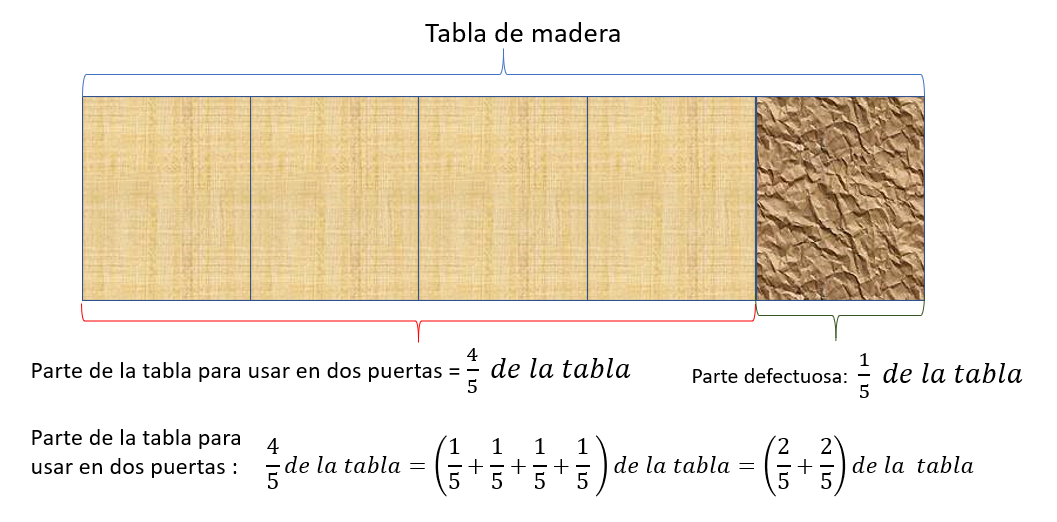
Con el primer método comienza elaborando la representación gráfica de la situación. Fíjate que puedes nuevamente aplicar lo que hiciste en la primera situación, al expresar la fracción que representa la parte de la pieza original que se usará para construir las dos puertas en la suma de cuatro veces un quinto. Hasta aquí has interpretado correctamente la situación, tanto en la representación gráfica como en la numérica. ¿Cómo determinas qué parte de la pieza original se utilizará en cada una de las puertas?
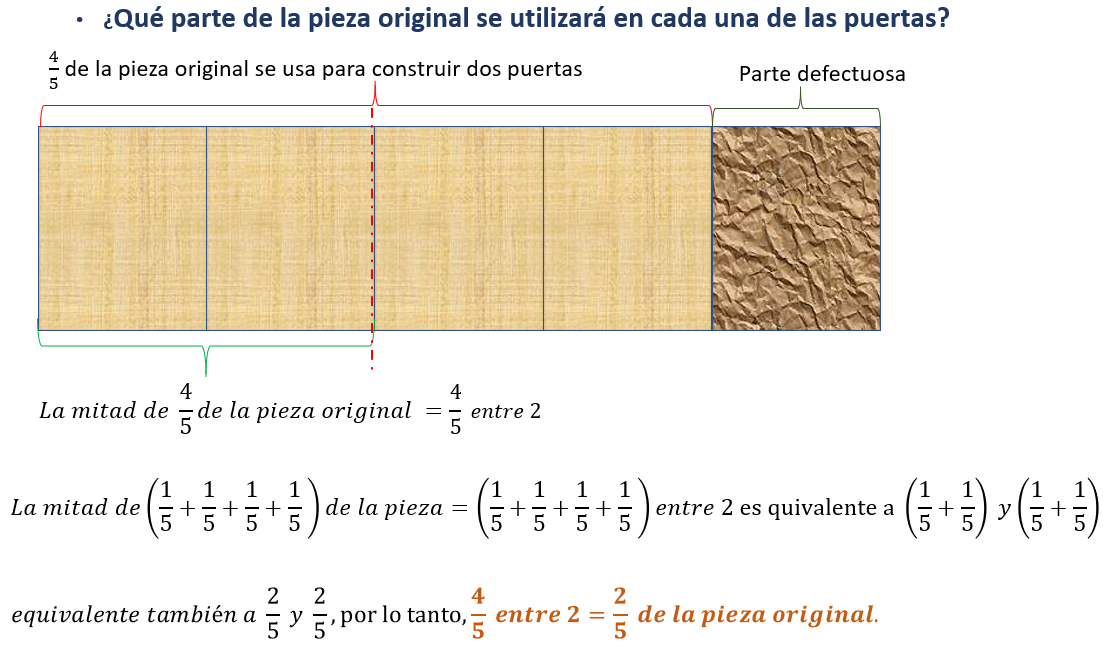
Identifica que, basada en la representación gráfica, se observa que la mitad de cuatro quintos, son dos quintos. Márcalo con una línea punteada de color rojo, luego expresa la mitad de cuatro quintos como cuatro quintos entre dos, a partir de ahí también suma cuatro veces un quinto, de manera semejante a como lo resolviste en la situación anterior, así podrás confirmar que dos quintos es la mitad de cuatro quintos. ¿Por qué antes de dos quintos, escribes cuatro décimos?

Para contestar esa pregunta, considera la representación gráfica de la situación. En tu procedimiento, indicaste que comenzaste marcando la mitad de cuatro quintos en el dibujo que representa la pieza original de madera, pues al marcar con una línea punteada la división entre dos de toda la pieza, la línea va en sentido horizontal de extremo a extremo de la pieza, incluyendo la parte defectuosa, entonces se divide cada quinto en dos partes, y así tienes la pieza original dividida en diez partes iguales.
Así pasaste de quintos a décimos y, de acuerdo con lo que se resalta, cuatro de esas diez partes se utilizarían para construir una puerta, lo que equivale a cuatro décimos y cuatro décimos es equivalente a dos quintos.
Esta es otra manera de obtener la respuesta de la pregunta. ¿Qué parte de la pieza original se utilizará en cada una de las puertas? Es dos quintos.
Repasa la solución de esta primera parte del desafío.
El reto de hoy:
Revisa los ejercicios que hiciste y elige uno que puedas compartir con algún familiar cercano, explícale como pudiste obtener tus resultados.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas
