¿Qué parte es?
¿Qué parte es?
Aprendizaje esperado: uso de fracciones del tipo m/2n (medios, cuartos, octavos, etcétera) para expresar oralmente y por escrito medidas diversas.
Énfasis: reflexionar acerca del significado de algunas fracciones al tener que representarlas gráficamente, o bien, para interpretarlas o compararlas.
¿Qué vamos a aprender?
Aprenderás el significado de algunas fracciones al tener que representarlas gráficamente, o bien, para interpretarlas o compararlas.
¿Qué hacemos?
En la sesión de hoy la idea es trabajar con una especie de rompecabezas.
En la siguiente imagen se encuentra la base del rompecabezas, y cuenta con todas estas piezas. La actividad consiste en que busques la forma de que este papel quede cubierto con las piezas, sin que se encime ninguna y sin que, sobre ningún espacio. Sí pueden sobrar, pero no se pueden encimar y tampoco quedar espacios en blanco.
Esta es sólo una idea, tú puedes acomodarlas de la forma que más te guste, respetando las indicaciones. En la siguiente imagen puedes apreciar, como les quedaron sus rompecabezas a algunos otros niños.
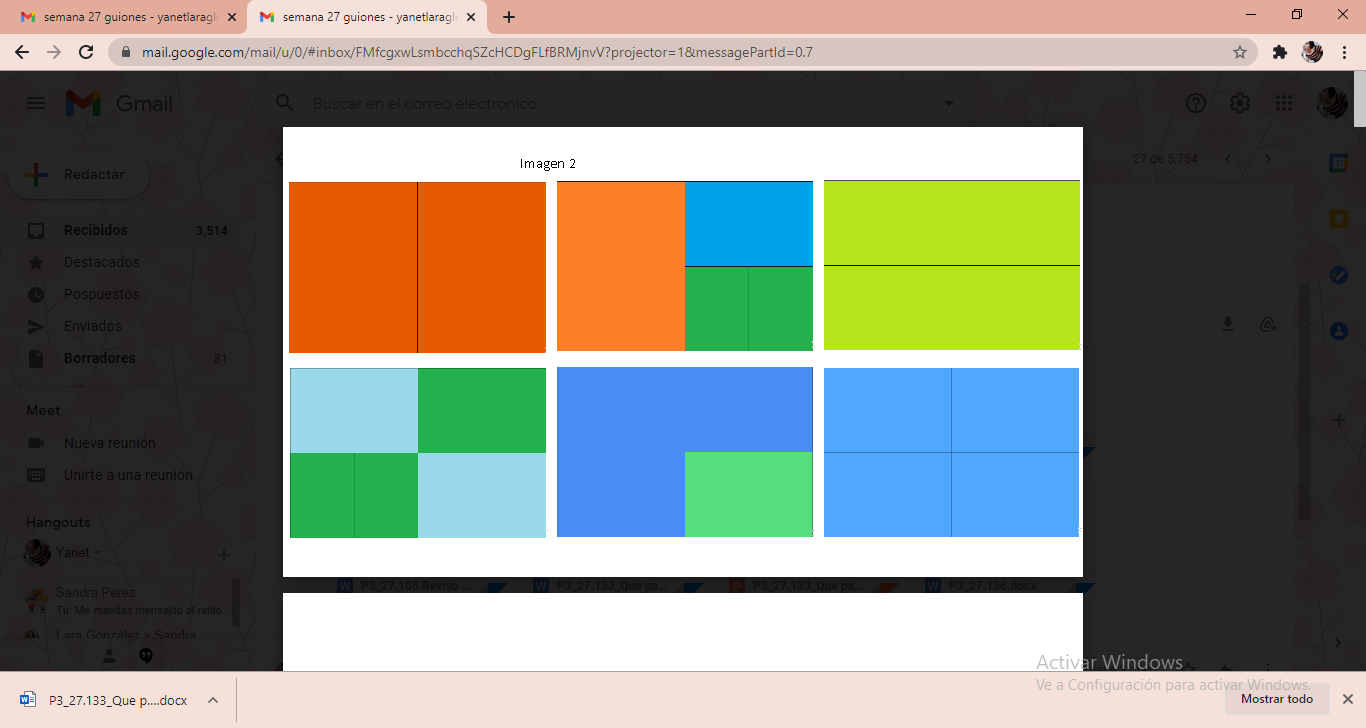
En este caso el recuadro representa un entero, y todas estas tarjetas, representan fracciones. Un entero puede estar conformado por diferentes fracciones, como los ejemplos que tú y algunas niñas y niños en casa armaron.
La pregunta en este caso es, ¿Puedes descubrir qué fracción representa cada color?
Se puede observar que al poner únicamente 2 anaranjadas, por ejemplo, se hubiera logrado cubrir todo el papel cascarón, eso quiere decir que el anaranjado representa los medios, cada uno de estos pedazos es 1/2.
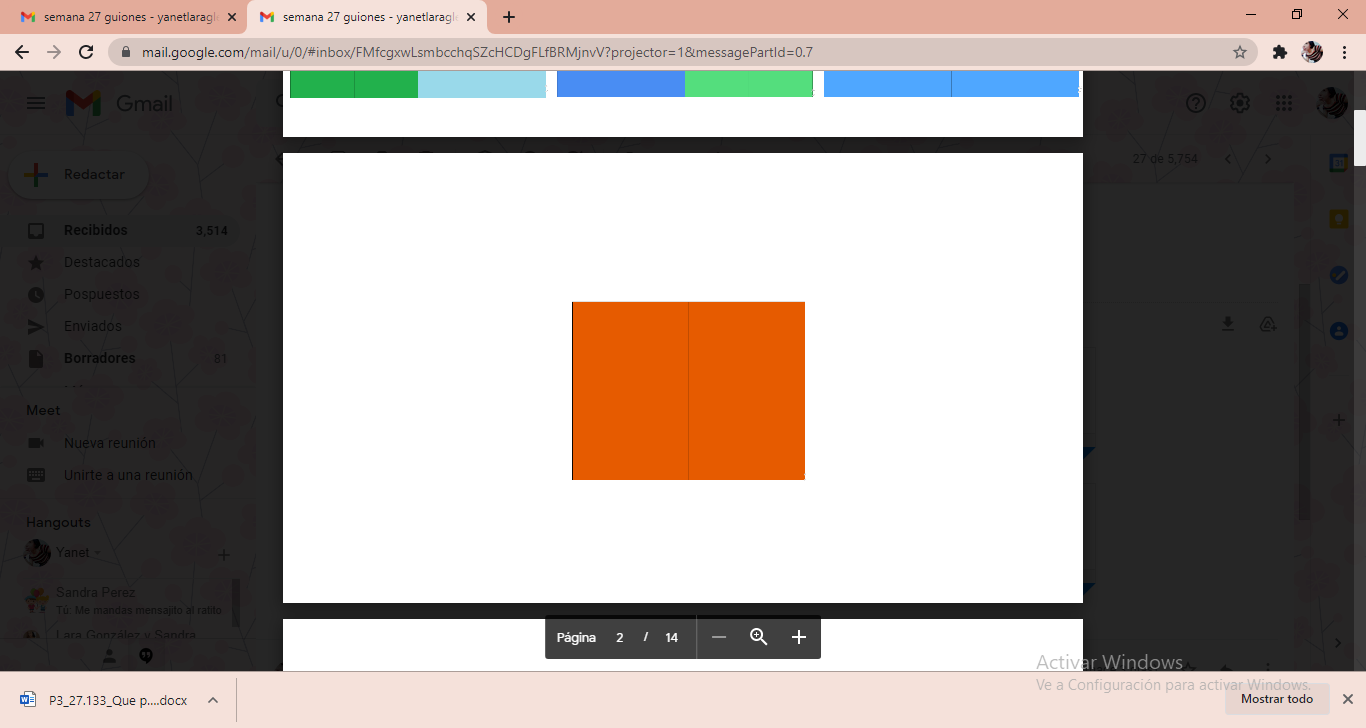
De esta manera, cada sección anaranjada es porque representa una parte de dos partes iguales en las que se dividió el entero y ambas secciones hacen 1 entero. Entonces, los azules serían cuartos porque observa la división entre: 1, 2, 3, 4, así 4 azules forman al entero nuevamente y todos son del mismo tamaño.
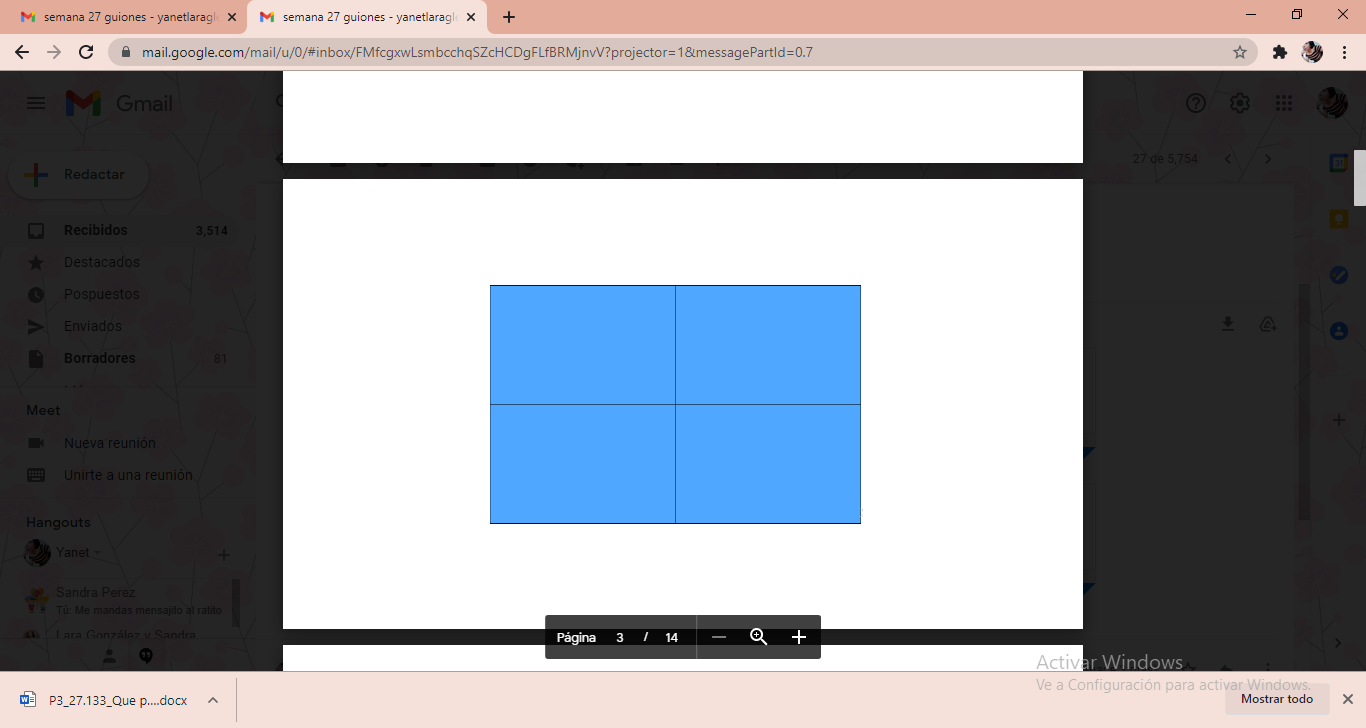
Por último, cada tarjeta verde es un octavo ya que: 1, 2, 3, 4, 5, 6, 7, 8 forman un entero. Estás 8 tarjetas verdes forman un entero y todas ellas tienen también el mismo tamaño entre ellas.
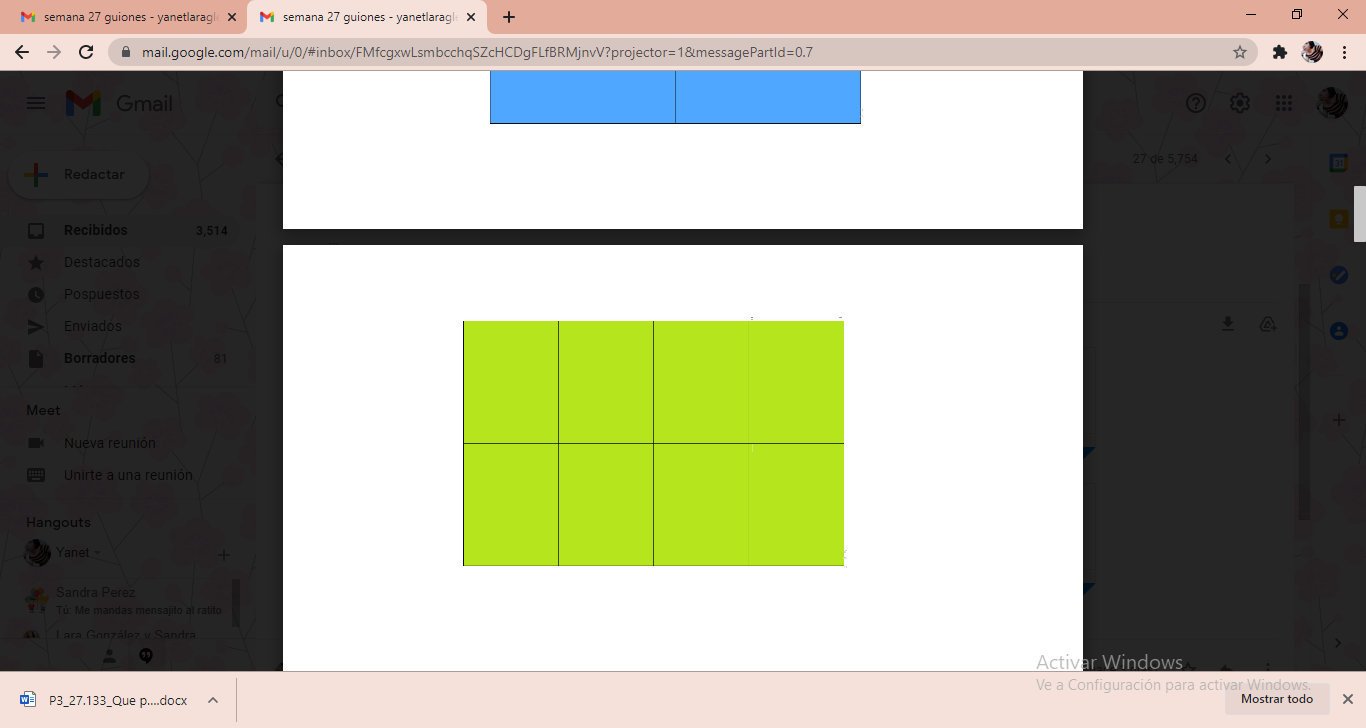
Recuerda que todo esto ya lo habías visto anteriormente en el desafío 32 de tu libro de texto Desafíos Matemáticos Tercer Grado páginas 73 y 74. Por ello, abre tu libro de texto en la página para recordarlo.
Para continuar, responde lo siguiente. Al colocar las siguientes dos tarjetas azules ¿Qué fracción del entero representan?
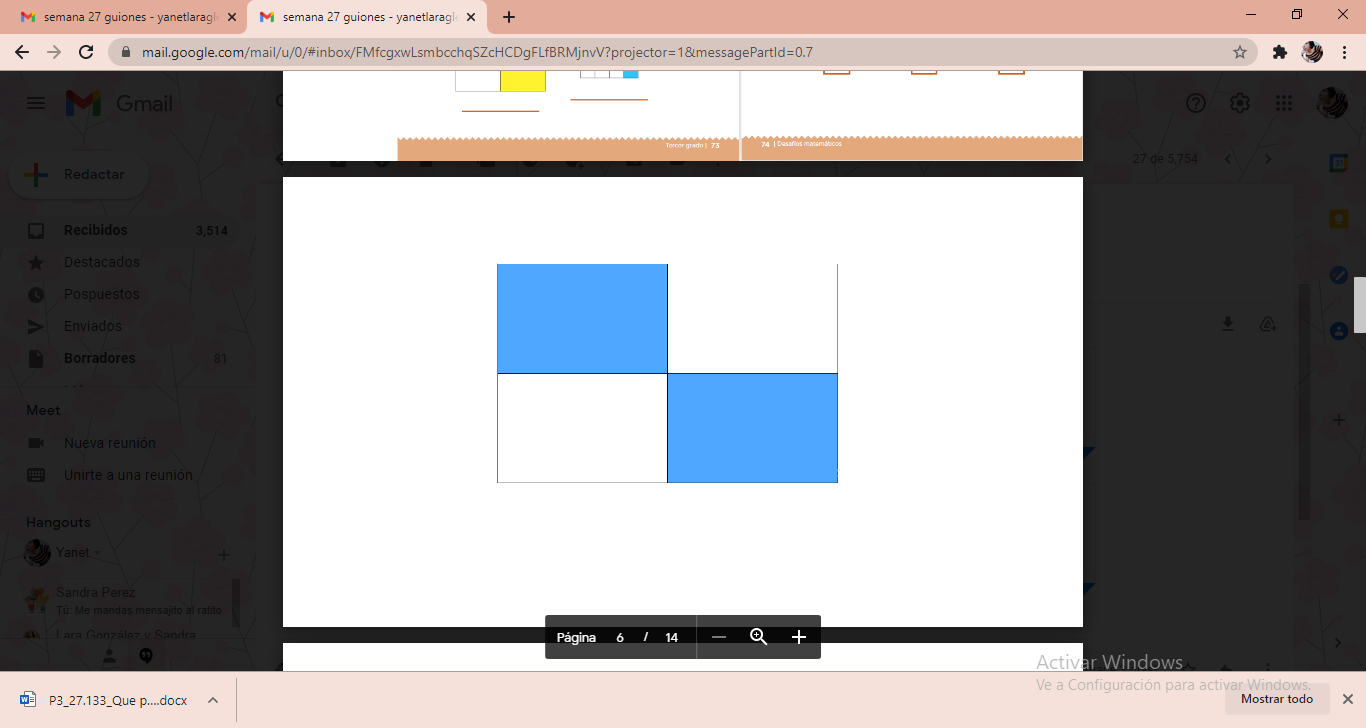
Como te habrás dado cuenta, necesitarías 4 de ellas para formar un entero completo, eso quiere decir que se está hablando de cuartos y sin son dos, ¿La fracción que representa es?
Exacto 2/4
De la misma forma, observa otra cosa importante, también puedes colocar estas 4 tarjetas verdes: 1, 2, 3, 4 y abarcan la misma superficie, ¿Lo ves?
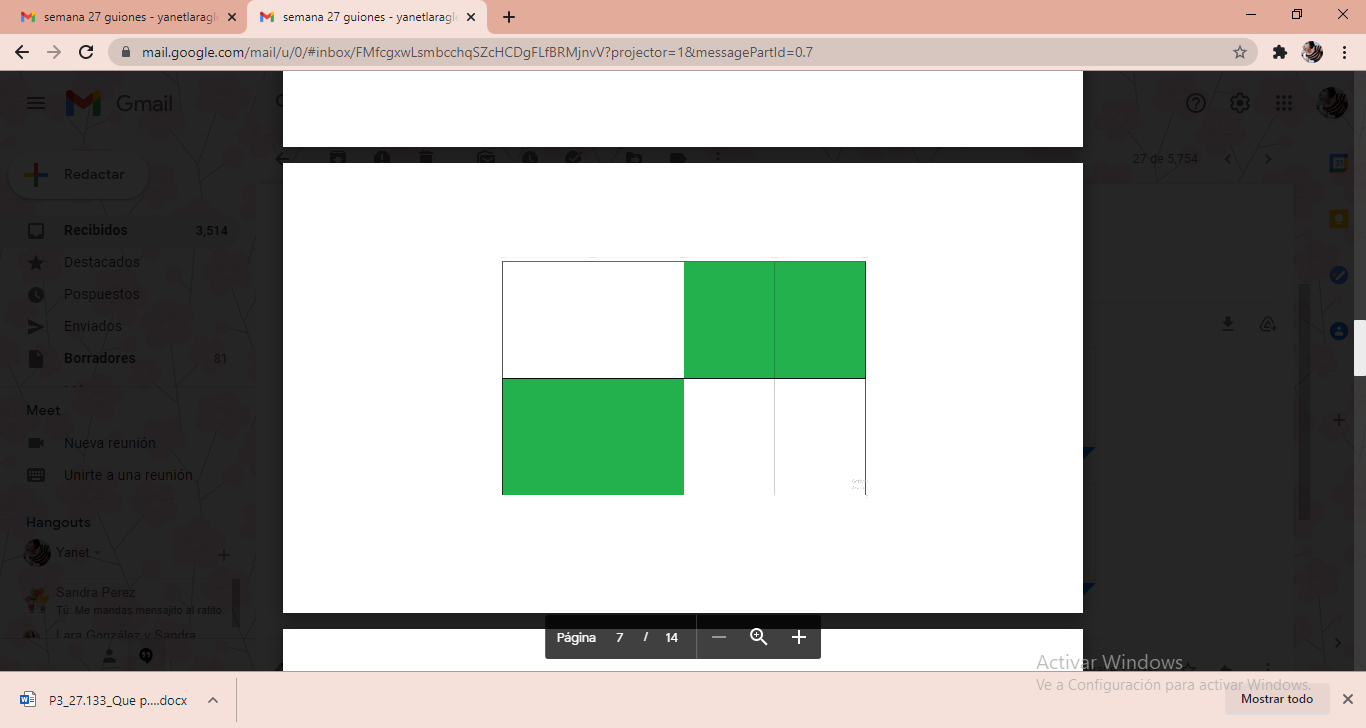
Si comparamos estas dos fracciones por este medio, ¿A poco son del mismo tamaño?
Puedes compararlos para que te des cuenta si lo son o no. Para ello, puedes retirar las tarjetas verdes y alinear las azules de lado izquierdo.
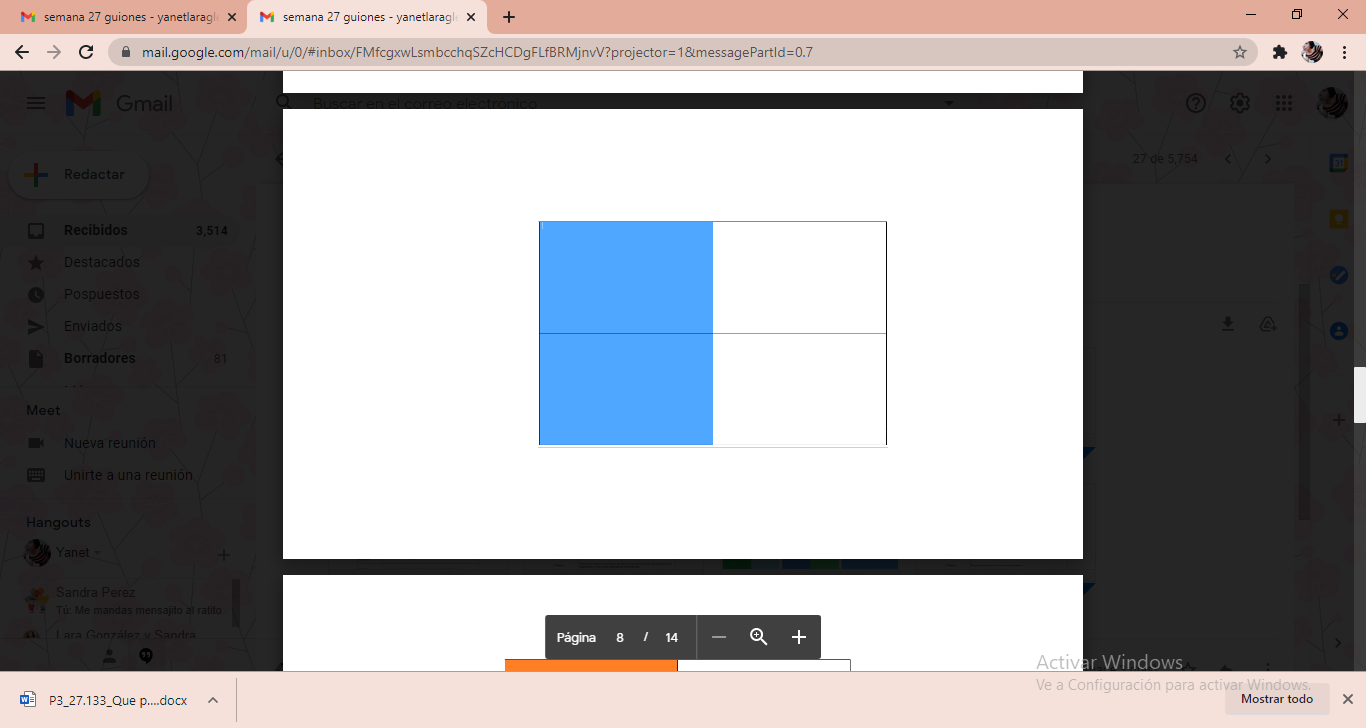
Ahora, sobrepone la tarjeta naranja a las azules. Y el resultado es que si representan la misma cantidad.
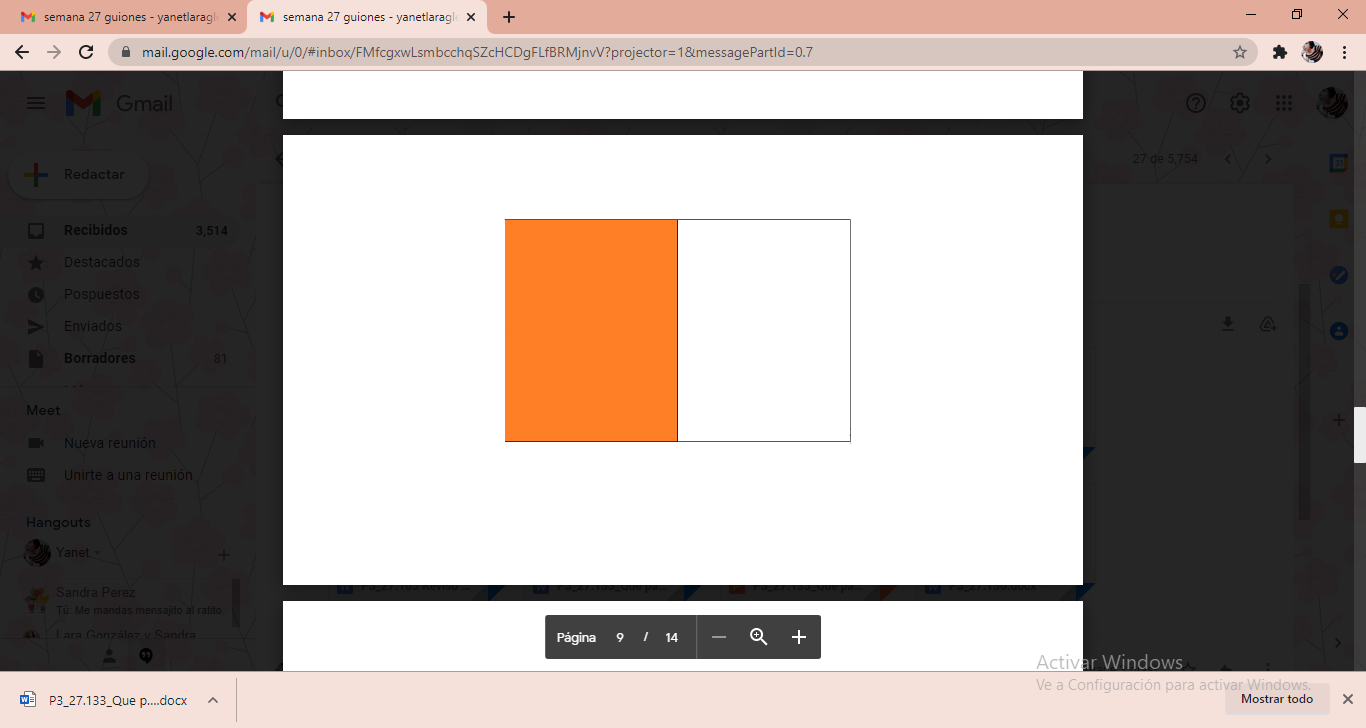
Entonces al comparar las superficies podemos decir que representan la misma porción del entero. Por eso, se les llama fracciones equivalentes, ya que sólo cambia la cantidad de porciones en la que se dividió el entero, pero representan la misma cantidad.
Así entonces, de pueden usar diferentes formas para representar un entero.
De este modo, si se colocarán las siguientes tarjetas, ¿Qué fracción le corresponde?
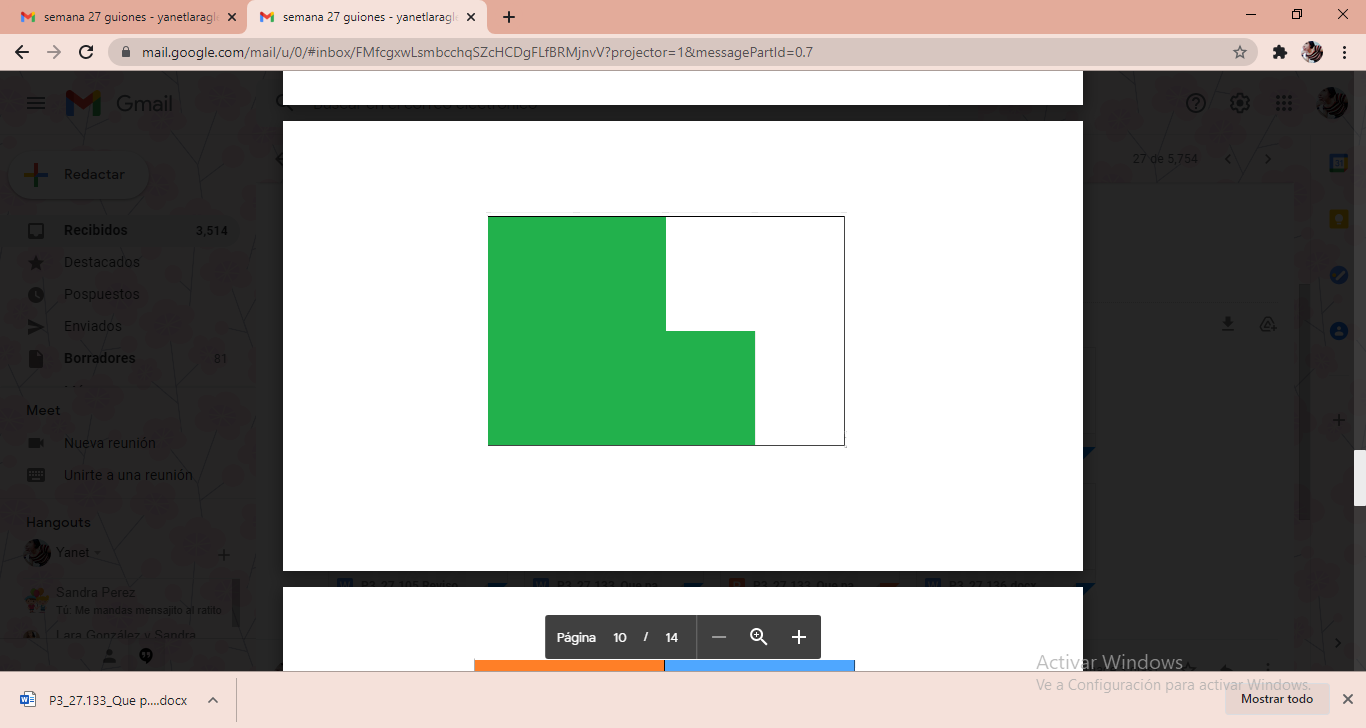
Las tarjetas verdes representan los octavos, así que el denominador sería el 8 y son 1, 2, 3, 4, 5, así que, ¿La fracción representada es?
Claro la respuesta es 5/8. Ahora busca si existe alguna fracción equivalente.
Al experimentar, seguramente te diste cuenta que está cantidad no tiene fracciones equivalentes mediante la comparación con las demás fracciones que estás trabajando, pero la cantidad 5/8 si tiene fracciones equivalentes a continuación te darás cuenta.
Si cada uno de los octavos de tu ejercicio, los parto a la mitad, ¿Cuántos pedazos quedan?
Muy buen, quedan 10. ¿Y con cuántos de esos cachitos se llenaría todo el entero?
Efectivamente, el entendió estaría completo con 16 pedazos. Eso quiere decir que serían 10/16
Para continuar, coloca una tarjeta anaranjada y una azul. ¿Qué fracción representa?
Sería un medio y un cuarto, pero la pregunta es, ¿Cómo quedaría representado en una sola fracción?
Para averiguarlo puedes sobreponer tarjetas azules encima de la anaranjada, pero una tarjeta no es suficiente, 2 tarjetas si lo son. Con dos tarjetas se cubre la sección naranja sin que falte o sobre y ahora sí, puedes decir que la sección representada con colores son 3/4.
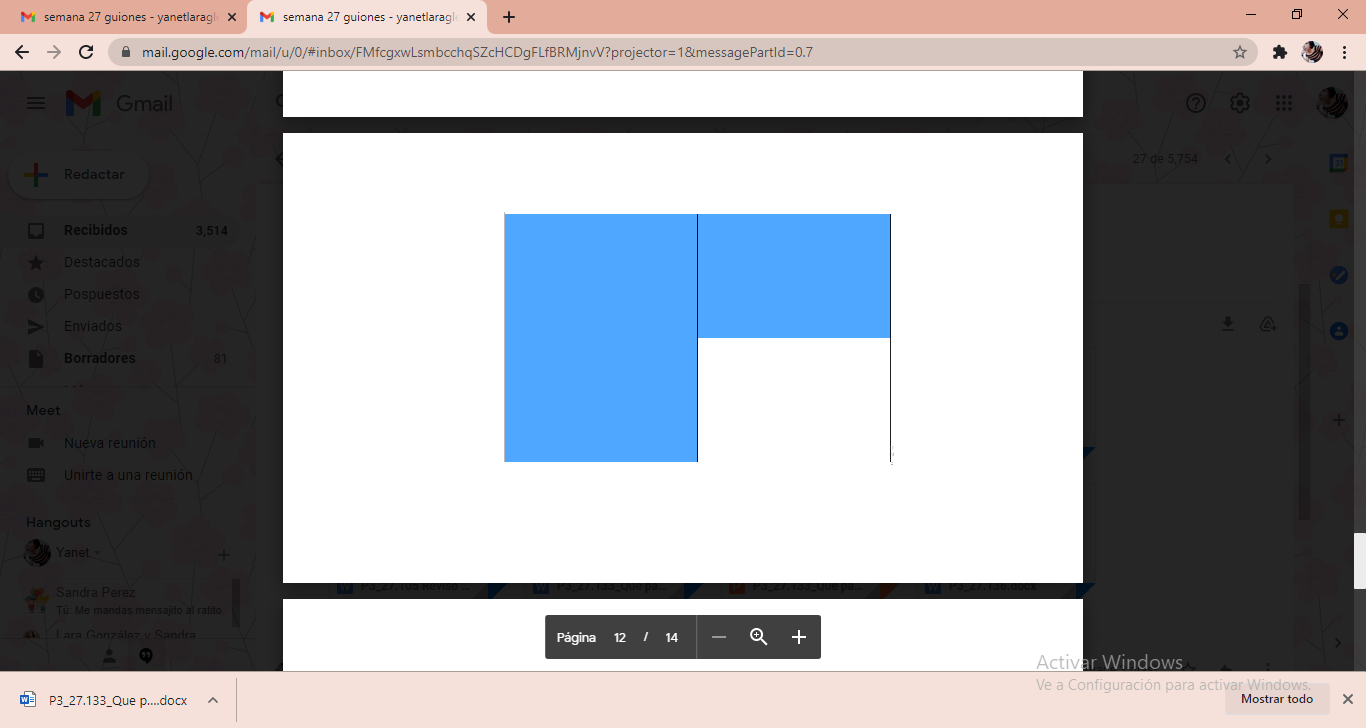
Al comparar la superficie que abarca, es fácil observar que es la misma superficie.
Para el siguiente ejercicio, coloca 3 tarjetas verdes y 2 azules, ¿Ahora qué fracción representa?
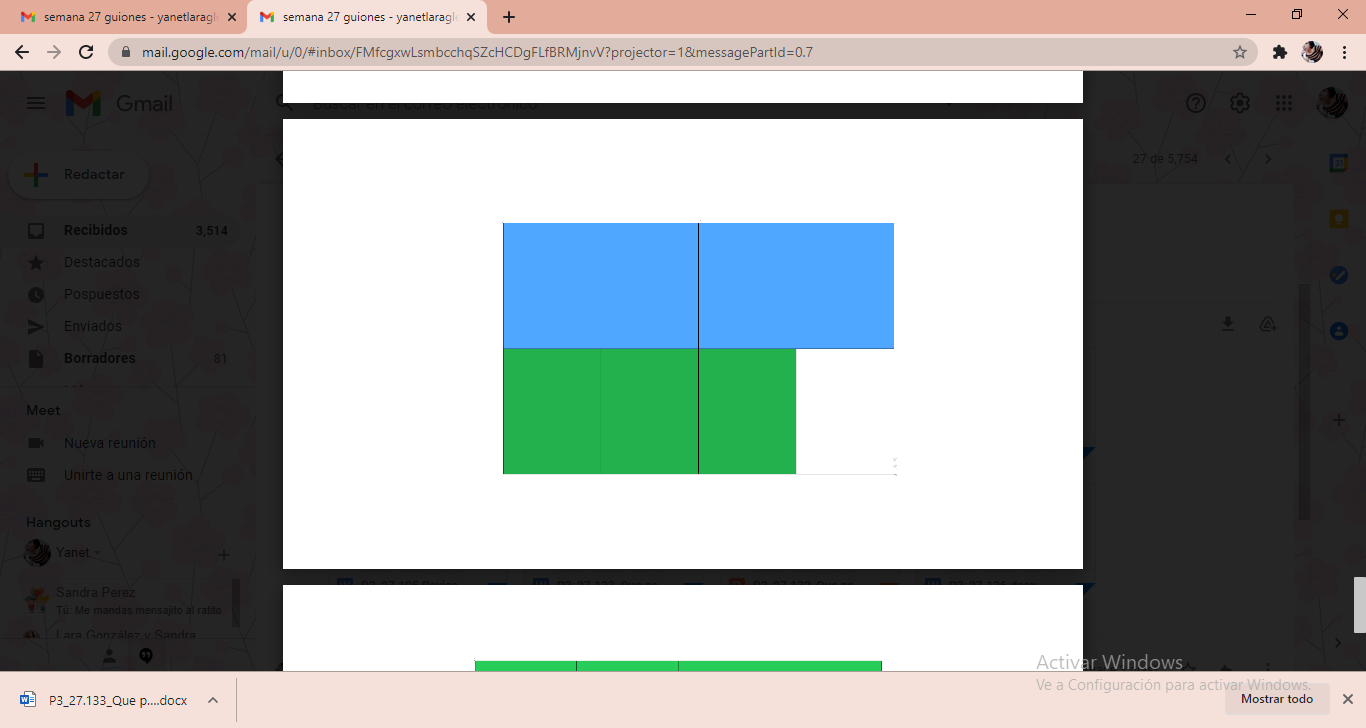
Nuevamente, medios no se pueden usar, porque quedaría cubierta la sección que no está cubierta, pero azules sí se pueden usar, entonces necesitas sobreponerlas a las verdes; pero no resulta bien.
Entonces debes usar octavos, al sobreponer octavos en las tarjetas azules obtendrás el resultado 7/8
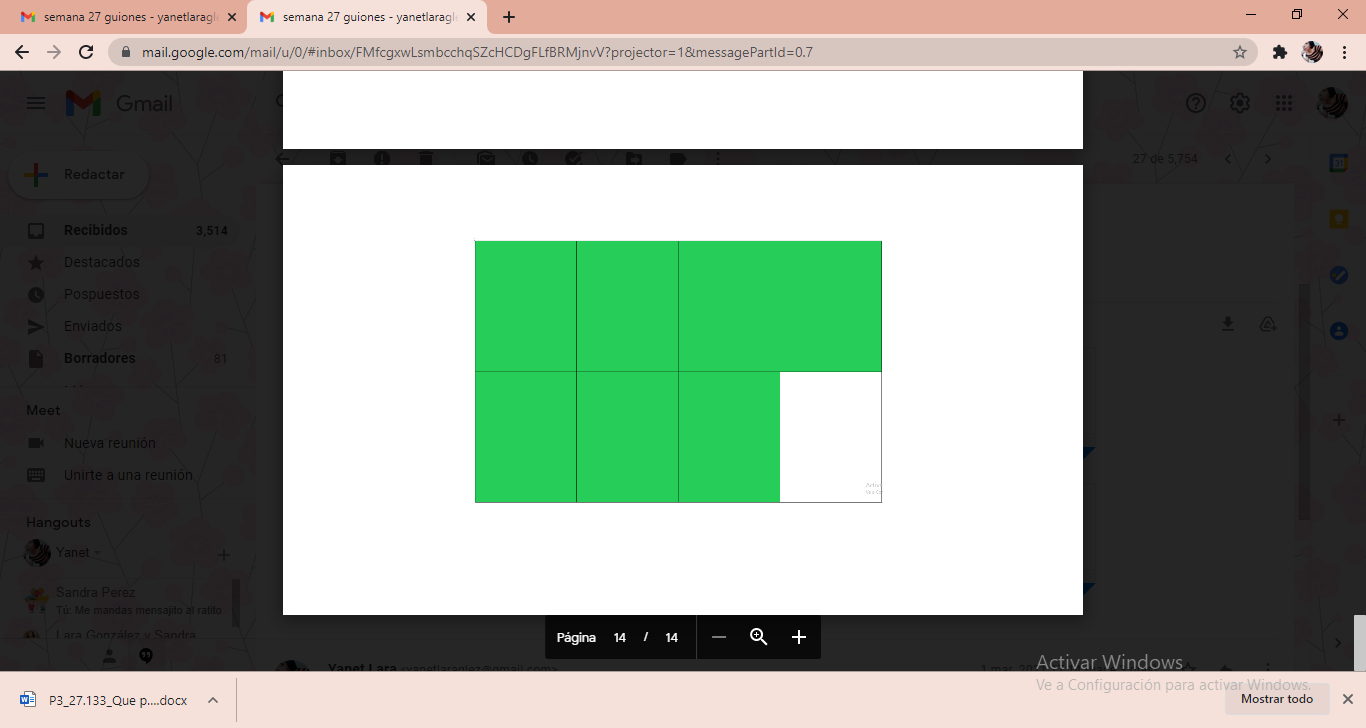
Ahora lo harás un poco diferente, verás las tarjetas, las acomodas y después interpretarás la fracción.
Coloca sobre el papel cascaron las equivalentes a un entero: puede ser una anaranjada, una azul y dos verdes. Recuerda que no pueden sobrar; antes piensa en dónde las vas a colocar.
Para ello, coloca las tarjetas restantes en el segundo entero. Con medios no, porque esta sección se cubriría, así que será con octavos. Toma tarjetas verdes y las sobrepones en la naranja y las azules luego ve contando las tarjetas verdes, son 1, 2, 3, 4, 5, 6, 7 ,8 ,9 ,10 y 11, la fracción representada es 11/8
Perfecto, así es, con las tarjetas que tienes ahora son 11/8 pero también puedes decir que es un entero ya que está completo, entonces 11/8 es equivalente a 1 entero 3/8 las dos opciones son correctas.
Como lo viste en el desafío anterior, el reto ahora es ubicar fracciones en la recta.
Pero antes representa la fracción 6/4
Seguramente, ¿Ya observaste que el numerador es mayor que el denominador? Cuando esto sucede, significa que la fracción indicada representa más de un entero.
Por ende, las tarjetas no se deben encimar y tampoco cambiar el tamaño porque entonces se afectaría la fracción, pero siempre se pueden usar más enteros.
Lo que sí, es que 6/4 también se puede representar con 3/2 al sobreponer 3 tarjetas anaranjadas y con 12/8 al sobreponer 12 tarjetas verdes, de esa manera, las tres fracciones son correctas ya que representan la misma cantidad de los enteros.
Ahora que sabes que algunas fracciones representan el mismo espacio y otras son más pequeñas o más grandes, vas a comparar fracciones, para ver que ya quedó muy claro todo.
Observarás dos fracciones y las representas, para entonces identificar la relación que hay entre ambas, es decir si una es mayor, es menor que o igual que la otra. ¿De acuerdo?
Primera actividad: 1/2 a 3/8
Coloca sobre un papel cascaron una tarjeta naranja y sobre los otros 3 verdes. Eso quiere decir que 1/2 es mayor que 3/8, coloca en medio de ambos el signo de >.
Muy bien, ahora con relación de 1/4 a 2/8
Coloca una tarjeta azul y sobre los otros 2 verdes, claramente se ve que son iguales. Entonces, coloca el signo de igual.
Ahora tienes 2/2 coloca las dos tarjetas anaranjadas del lado izquierdo y el símbolo de “mayor que” en medio y coloca del otro lado una fracción que sea menor que 2/2
Entonces, 2/2 es un entero, así que cualquier fracción menor que un entero cumple el requisito. La pregunta es, ¿Cómo se leería?
Exacto 2/2 es mayor que 1/4
Debes tener en cuenta que un entero y una fracción pueden ser de cualquier cosa, en este momento usaste rectángulos, pero también pueden ser en círculos, triángulos, rombos, rectas, pasteles, manzanas, naranjas, piñas, etcétera.
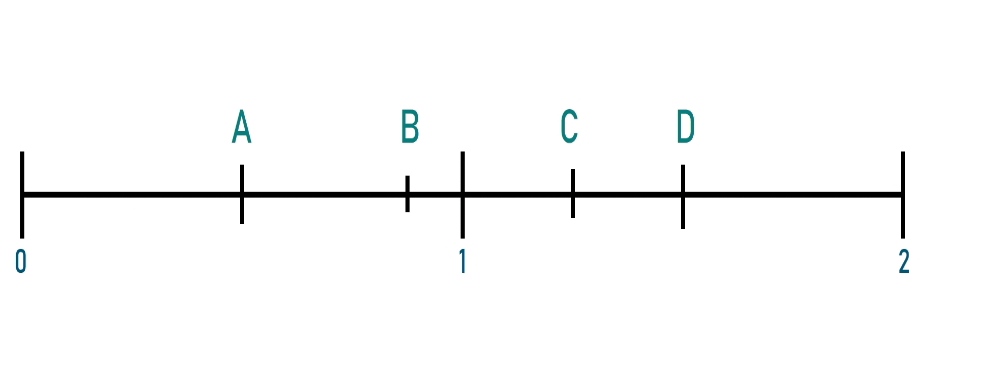Las fracciones son útiles en la recta, en figuras e incluso con números, en esta ocasión vas a trabajar con una recta. A continuación, debes relacionar las siguientes fracciones con la marca a la que corresponden en la recta.
Las fracciones son: 1/2, 3/2, &/4, 7/8
A cada fracción de darás su letra correspondiente: A, B, C y D. Como puedes darte cuenta en la recta numérica están representados dos enteros.
Esto porque del cero al 1 está representado un entero y del 1 al dos otro entero. También hay fracciones que son menores que un entero y otras mayores que el entero.
Por ejemplo, las menores son 1/2 y 7/8. Las mayores a un entero son 5/4 y 3/2. La pregunta es, ¿Cómo pudiste distinguirlos tan rápido?
Muy cierto, cuando el numerador es menor que el denominador, la fracción es menor a 1 entero y cuando el numerador es mayor al denominador, es mayor a un entero.
Eso significa que estas dos fracciones: 1/2 y 7/8 deben corresponder a los puntos A y B. Por lo tanto, 5/4 y 3/2 a los puntos C y D.
Ahora, ¿A qué fracción corresponde el punto A?
Efectivamente la letra A indica un segmento que equivale a 1/2. Y eso significa que la letra B corresponde a 7/8. Para comprobarlo, divide el entero completo en 8 partes (con un plumón divide los medios en dos y luego los cuartos nuevamente en dos para que queden) así se puede observar entonces como la letra B representa la fracción 7/8
Cuando no te sientas con la seguridad de calcular dónde dividir para que quede en partes iguales, ¿Qué más puedes hacer?
Hay dos opciones más, una es medir los segmentos y dividir lo que mide y la segunda es compararla con algún listón, tira, etcétera e ir realizando los dobleces necesarios para comparar tu recta numérica, como lo hiciste anteriormente.
Ahora falta encontrar las fracciones que corresponden a: C y D. Es más fácil encontrar los medios, debido a que sólo se divide el entero en dos, entonces del cero al 1 ya tienes 2/2, 2/3 se encontrarán a la mitad del segundo entero, es decir, del 1 y el 2.
¿Cuál de las dos fracciones consideras que se encuentra en medio de 1 y 2?
En efecto, se encuentra 3/2 que corresponde a la letra D. Recuerda que también se puede expresar como 3/2 o bien, puedes decir que es 1 entero 1/2
Entonces la letra C estará representando 5/4 y eso lo puedes comprobar porque en el primer entero ya tienes 4/4 y si divides esta parte en cuartos te das cuenta de que esta marca representa ¼ así que aquí se encuentra 1 entero 1/4 o 5/4 como aquí lo menciona por ello coloca la fracción debajo de la letra C.
Actividad extra.
Ahora puedes encontrar otros puntos, ¿Qué fracción quisieras encontrar?
Tal vez te gustaría encontrar la fracción que estaría en medio de 1 y C. A este punto le otorgaras letra E.
Para empezar, es mayor que 1, y por el tamaño de la sección se estableció que C representa cuartos y D medios por lo tanto debe ser en octavo, eso lo puedes comprobar midiendo las fracciones.
Al observar queda claro que es el primer octavo pasando el entero así que sería 1 entero 1/8, o 9/8
Por último, podrías ubicar la fracción en la recta ¼ claramente, como 1/4 y el numerador es menor que el denominador, sé que se debe encontrar entre 0 y 1
De esta manera, A representa 1/2 porque es la mitad de un medio, entonces 1/4 se encuentra aquí, a la mitad de 0 y ½ es importante que coloques una marca calculando que sea la mitad del segmento 0-A para identificar la fracción. A este punto le pondrás la letra F.
Excelente terminaste.
Recuerda que las fracciones son representaciones de alguna sección de uno o varios enteros y que se pueden expresar de diferente manera según la cantidad de partes en que dividamos al entero. También recuerda que existen fracciones que representan la misma porción que otras y se llaman fracciones equivalentes.
El reto de hoy:
Elije 3 fracciones entre el 0 y el número 5, de acuerdo con estás, en tu cuaderno realiza una línea fraccionada dónde adjuntes las fracciones que elegiste de manera correcta. No olvides que todo lo que aprendes lo puedes externar a tu vida cotidiana.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
