Problemas aditivos con números fraccionarios II
Problemas aditivos con números fraccionarios II
Aprendizaje esperado: resolución de problemas aditivos con números naturales, decimales y fraccionarios, variando la estructura de los problemas. Estudio o reafirmación de los algoritmos convencionales.
Énfasis: resolver problemas aditivos con números fraccionarios que tienen diferente denominador. (2/3)
¿Qué vamos a aprender?
Aprenderás a resolver problemas aditivos con números naturales, decimales y fraccionarios, variando la estructura.
Para explorar más puedes revisar el libro de texto de Desafíos matemáticos de 6º, se explica el tema a partir de la página 15.
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/15
¿Qué hacemos?
A continuación te presentamos información y algunas actividades que te ayudarán a resolver problemas aditivos con números fraccionarios que tienen diferente denominador.
Te vamos a explicar qué son las fracciones, pero no sólo desde un punto de vista real, sino desde el punto de vista de los números, el cual te ayudará a entender las operaciones con fracciones.
Una definición de las fracciones dice que es una forma de representar las partes de un todo. Por ejemplo, tenemos esta barra rectangular.

Podríamos dividirla en 2 partes iguales:

La parte que está coloreada de verde, se representa como una fracción de esta forma:
Donde:
El número de abajo, el denominador, representa las partes totales en el que se ha dividido el todo.
El número de arriba, el numerador, representa las partes a las que queremos hacer referencia.
Podemos dividir el todo en las partes que queramos, aunque las partes deben ser iguales.
Ahora dividimos la barra en 3 partes iguales.

¿Cómo representamos en forma de fracción la parte pintada de verde? Así:
Ahora en el denominador (el número de abajo) tenemos un 3, que son las partes en las que hemos dividido la barra, y en el numerador (la parte de arriba) tenemos un 2, que son las partes pintadas de verde y a las que queremos hacer referencia.
Si la dividimos en 4 partes y pintamos de verde sólo 1:
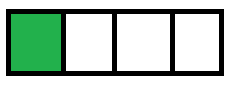
Esta parte se representaría:
Ahora bien, esta definición de qué son las fracciones sólo es válida si el número al que estamos representando es menor o igual que 1, ya que estamos haciendo referencia a una o más partes del todo.
Sin embargo, también podemos representar en forma de fracción el todo completo, es decir, si dividimos la barra en 3 partes y queremos hacer referencia a las 3 partes.

Se representaría:
El numerador y el denominador son iguales, porque las partes en las que se divide la barra y a las que hacemos referencia son las mismas. Si realizamos la división, nos da como resultado la unidad:
Esto me lleva a decirte que las fracciones son otra forma de representar los números, tanto los decimales como los enteros. Es como dejar la división indicada sin llegar al resultado final.
En el último ejemplo hemos representado las 3 partes que forman la barra completa, es decir, el todo. Si realizamos la división nos da la unidad.
Las fracciones anteriores podemos expresarlas también como números decimales si terminamos de realizar la división:
Hasta ahora, el numerador siempre ha sido menor o igual que el denominador, pero, ¿El numerador puede ser mayor que el denominador?
Por supuesto que sí.
En ese caso, las fracciones ya no representan partes de un todo, sino un reparto o, mejor dicho, una división.
Ahora que ya tienes un poco más claro qué son las fracciones desde el punto de vista matemático, vamos a ver otro concepto: Las fracciones equivalentes.
Las Fracciones Equivalentes son aquellas que, al realizar su división, tienen el mismo valor o, dicho de otra forma, representan al mismo número (decimal o entero).
Vamos a verlo más despacio con algunos ejemplos:
Tenemos una barra, dividida en 2 partes iguales y queremos representar en forma de fracción la parte coloreada de verde.

Las 2 partes en las que hemos dividido la barra serán el denominador y la parte de verde será el numerador.
Si realizamos la división, la fracción tiene un valor de:
Ahora queremos representar la misma parte pintada de verde, pero en este caso la barra va a estar dividida en 4 partes. Para que la parte de verde sea igual que, valga la redundancia, la parte de verde del caso anterior, le corresponderán 2 partes de la barra:

Las 4 partes en la que hemos dividido la barra serán el denominador y las 2 partes de verde serán el numerador:
Y esta fracción tiene un valor de:
Como la parte de verde de ambos casos es igual, el valor de cada fracción es el mismo (no podía ser de otra forma).
Por tanto, las fracciones:
Son fracciones equivalentes y son dos formas distintas de representar al mismo número.


De la misma forma, si queremos representar la unidad en forma de fracción, tenemos infinitas formas de hacerlo, siempre y cuando el numerador y el denominador sean iguales; ejemplos:

= 1

= 1

= 1
El valor de todas estas fracciones es 1.
Por tanto, son también fracciones equivalentes y son distintas fracciones para representar una misma unidad.
Por último, es lo mismo repartir 10 unidades entre 4, que 5 unidades entre 2 o que 100 unidades entre 40. El resultado de todos los repartos es el mismo:
Por tanto, estamos hablando de fracciones equivalentes.
Actividad 1
Ahora vamos a enlazar la información que se recuperó con el siguiente problema del libro de texto.
Después de este breve recordatorio, vamos a nuestro libro de texto, a la página 15, al desafío 6.
Algo de lo que acabamos de recordar de la clase anterior, ¿Podrá servirnos para buscar la solución del siguiente problema?
Vamos a leer el problema 2 ¿Qué peso pondrían en el platillo izquierdo para que la balanza se mantenga en equilibrio?
¿Todos sabemos lo que es una balanza? ¿Para qué sirve? ¿Dónde se utiliza?
La balanza es un instrumento que nos permite comparar el peso de dos objetos al mismo tiempo; para ello debemos colocar en cada uno de sus platillos un objeto, lo cual nos permitirá ver cuál pesa más, cuál menos o si pesan los mismo.


En la actualidad, cuando vamos al mercado o a algún lugar donde vendan algo que se tiene que pesar, se suelen emplear básculas que nos dan el peso de los objetos, algo parecido a lo que nos permite hacer la balanza.
Observemos la ilustración que aparece en la página 15 del libro de texto. En el platillo derecho de la balanza, frente al niño, tenemos tres cilindros con diferentes pesos:
| 1 kg |
En el platillo izquierdo únicamente tenemos un cilindro con:
Leamos nuevamente el problema: ¿Qué peso pondrías en el platillo izquierdo para que la balanza se mantenga en equilibrio?”
¿Qué es mantener el equilibrio? Exacto, tenemos que igualar el peso que hay en un platillo con el del otro platillo.
Entonces ¿Cómo podemos saber cuánto peso le falta al platillo del lado izquierdo para lograr la igualdad en el peso y, en consecuencia, encontrar el equilibrio?
¿Ya lo pensaste bien? Podemos usar la información que recordamos de clases anteriores.
Primero necesitamos saber cuánto peso en total tenemos en el platillo derecho. ¿Cómo podemos hacerlo? Para apoyarnos te presento los pesos del platillo derecho.
| 1 kg |
Piensa ¿Qué podemos hacer?
Bien. Hay que realizar una suma, pero ¿Cómo vamos a sumar estas fracciones?
Hay que pensar qué camino o proceso se te hace más fácil llevar a cabo, te comparto uno de los muchos caminos para solucionarlo.
Observa: Tenemos 1kg; las siguientes dos fracciones son tercios, porque las dos tienen en el denominador un tres, y tienen un mismo denominador, lo que significa que tenemos 2 tercios.
En total, en el platillo derecho tenemos una fracción mixta.
Ahora sí ¿Cuánto nos faltará para igualar la cantidad con el peso del platillo izquierdo.
¿Qué hacemos ahora?
Necesitamos pasar la fracción mixta a una fracción impropia para poder trabajar con ellas. En un entero, ¿Cuántos tercios hay? 3 y 2 más que tenemos, ¿Cuántos tercios hay en total?
Ahora podemos observarlo mejor para tomar una decisión.
?
Una resta, pero ¿Cómo colocamos las cantidades que vamos a restar?
Tenemos que quitarle al platillo derecho lo que ya tenemos en el platillo izquierdo para encontrar lo que nos falta.
¿Cómo resolvemos la resta? Hay que encontrar fracciones equivalentes, lo que significa que las dos cantidades deben tener el mismo denominador. Recordemos que lo que le sucede al numerador le tiene que suceder al denominador.
¿Ya te acordaste? Debemos encontrar fracciones equivalentes a las que tenemos para poder restar. En este caso, una forma en encontrar las fracciones equivalentes es multiplicando los denominadores lo cual nos da un resultado de 15, lo que nos permite saber que las fracciones equivalentes tendrán de denominador 15. Entonces, podemos hacer lo siguiente:
Ya tenemos las fracciones equivalentes ahora sí, a restar:
¿Qué peso pondrían en el platillo izquierdo para que la balanza se mantenga en equilibrio?
¡FELICIDADES, LLEGAMOS A LA RESPUESTA!
Actividad 2
Continuemos en la página 16 de nuestro libro de texto con la consigna 2 de nuestro desafío 6, resuelve individualmente estos problemas, cuando hayas terminado todos, reúnete otra vez con tu equipo para comparar y comentar sus resultados.
Problema 1
¿Cuánto hay que agregar a para obtener ?
¿Ya se dieron cuenta? Es muy parecido al que resolvimos en el problema anterior, así que manos a la obra. Observamos las fracciones con las que vamos a trabajar.
¿Cuánto hay que agregar a ¾ para obtener 6/7?
¿Crees que de esta manera podemos resolverlo? Tenemos que buscar la fracción que falta para que logremos llegar a 6/7.
¿Cómo le podemos hacer? Claro, podemos hacer una resta.
Porque la resta es la operación inversa a la suma y queremos encontrar la diferencia o parte que falta a ¾ para que sea igual a 6/7. Con una resta podemos solucionarlo de este modo, colocamos la fracción mayor al inicio restamos la fracción más pequeña y la escribimos después, quedando así:
Como ya sabemos, primero debemos encontrar fracciones equivalentes de cada una de las fracciones dadas, y el numerador tiene que ser igual. Ya habíamos visto que multiplicando los denominadores podemos obtener un denominador igual para ambas fracciones, sin olvidar que lo que le sucede al denominador le debe ocurrir al numerador.
Ahora encontremos las fracciones equivalentes.
Y la segunda fracción equivalente es:
Ahora ya podemos hacer nuestra resta:
Nuestra respuesta a:
¿Cuánto hay que agregar a para obtener ? es 3/28
Muchas felicidades, hasta este momento vamos muy bien.
Gracias por la atención y disposición. En la próxima clase resolveremos los problemas 2, 3 y 4 de la página 16 de tu libro de texto. Cuídate y te esperamos con mucha actitud para seguir aprendiendo.
El reto de hoy:
Intentar resolver los problemas 2, 3 y 4 de la página 16 de tu libro de texto.
Si en tu casa hay otros libros relacionados con el tema, consúltalos, así podrás saber más, si no cuentas con estos materiales no te preocupes, en cualquier caso, platica con tu familia sobre lo que aprendiste, seguro les parecerá interesante.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Consulta los libros de texto en la siguiente liga.