Pi. Relación entre circunferencia y diámetro
Pi. Relación entre circunferencia y diámetro
Aprendizaje esperado: calcula la longitud de una circunferencia mediante diversos procedimientos.
Énfasis: obtiene la medida de la circunferencia y el diámetro de varios círculos y advierte que el cociente del primero sobre el segundo es una constante llamada pi (π). Reconoce el producto obtenido entre π y la longitud del diámetro como un procedimiento más para calcular la longitud de la circunferencia.
¿Qué vamos a aprender?
Calcularás la longitud de una circunferencia mediante diversos procedimientos. En este proceso vas a obtener la medida de la circunferencia y el diámetro de varios círculos y advertir que el cociente del primero sobre el segundo es una constante llamada pi (π), y a reconocer el producto obtenido entre π y la longitud del diámetro como un procedimiento más para calcular la longitud de la circunferencia.
¿Qué hacemos?
Revisarás la importancia que tiene una figura geométrica, se trata del círculo.
En esta sesión y la siguiente estarás revisando algunos elementos y aspectos relevantes y propios del círculo, por ejemplo, ¿Cuál es una de las principales características con la cual sabes que una figura geométrica es un círculo? Es decir, por qué sabes que esta figura es un círculo y no un triángulo o un cuadrado.
Porque se trata de una línea curva que lo limita, es la circunferencia, es decir, su perímetro o contorno, esa es una característica representativa de un círculo.
En esta sesión vas a usar la imaginación, para identificar una figura o cuerpo geométrico como para trazarlos se requiere imaginar, por ejemplo, cómo son sus lados, caras o aristas e imaginar en qué lugar se colocarán las bases o pestañas para armar un cuerpo.
En el estudio de las formas geométricas es indispensable la observación y la imaginación, como ya se ha señalado antes, y en este caso del círculo no será la excepción, pues dentro de las figuras geométricas básicas está el círculo, desde tiempo remotos se ha estudiado. Como ejemplo se tienen las imágenes siguientes:
 |
 |
 |
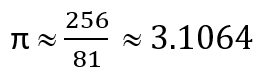 |
En el año de 1800 antes de nuestra era, en el antiguo Egipto, en el papiro de Rhind se muestran diferentes figuras geométricas, entre ellas, el círculo y el valor aproximado de Pi es
De la misma época, se han encontrado tablas con escritura cuneiforme de los babilonios que representa valores aproximados de Pi.
En el siglo III antes de nuestra era, es reconocido el interés del matemático griego Arquímedes por el círculo. Como dato curioso, se cuenta que antes de su muerte sus últimas palabras fueron: “No toque mis círculos”, haciendo referencia al problema que en ese momento estaba resolviendo.
Que expresión tan curiosa, seguramente estaba muy concentrado en la resolución de su problema que no se dio cuenta qué ocurría, así le ocurrió porque Arquímedes tenía fama de apasionarse por los problemas y olvidarse hasta de comer.
Lo cierto es que el estudio del círculo ha permitido grandes avances e inventos, como, por ejemplo, la rueda, que es uno de los más grandes inventos del hombre.

La rueda tiene forma circular, además el estudio del círculo junto con el estudio de la astronomía entre otras cosas permitió considerar que la forma de la Tierra era redonda y no plana.
El círculo es una figura geométrica básica. Si observas a tu alrededor encontrarás que una gran cantidad de objetos tienen forma circular.
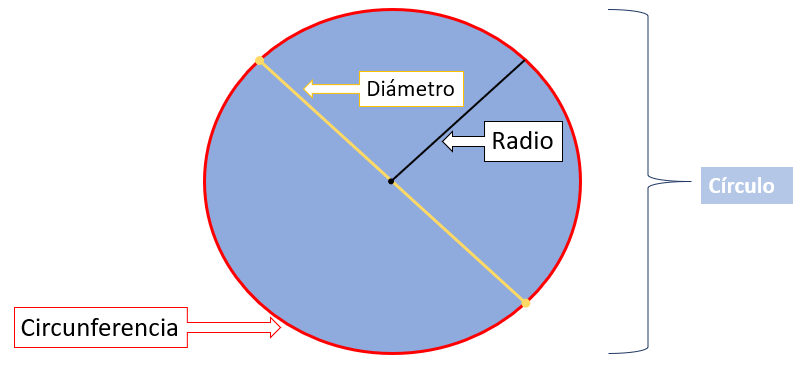
Ahora como primera actividad debes reconocer algunas partes del círculo. La actividad que vas a realizar es identificar en una sopa de letras algunas palabras que están relacionadas con el círculo. En este caso te ayudará recordar algunas de las partes de un círculo que viste en quinto grado de primaria y que están indicadas en la siguiente figura del círculo.

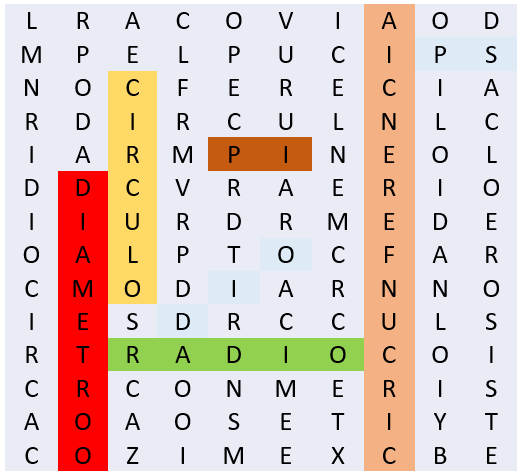
Con esta ayuda ya debes conocer todas las palabras que vas a buscar, entonces, aquí está la sopa de letras. Observa detenidamente e identifica algunas palabras que corresponden a las partes del círculo que están indicadas en la figura.

Búsca las palabras y enciérralas. Encierra circunferencia, anótala en el espacio que le corresponde en la imagen para que, posteriormente, recuerdes su concepto.
Busca y enciérra la palabra “radio”.
Ahora busca y encierra otra línea del círculo o algún otro elemento que se relaciona con el círculo. Busca la palabra “diámetro”.
Ya solo faltan dos. Busca y encierra la palabra “círculo”. Ya la que falta es una palabra de dos letras. Recuerda que tiene que ver con el círculo y la circunferencia, es la palabra “Pi”.
Ya están las cinco palabras, “circunferencia”, “radio”, “diámetro”, “círculo” y “Pi”.
Ahora recuerda a qué se refiere cada una.
- La circunferencia es la línea que está alrededor del círculo. La circunferencia es el perímetro del círculo y todos sus puntos están a la misma distancia del centro del círculo.
- El radio es la línea recta que une el centro con cualquier punto de la circunferencia.
- El diámetro es el segmento que une dos puntos de la circunferencia y que pasa por el centro. El diámetro mide el doble del radio.
- El círculo es una figura geométrica redonda y plana. El círculo es la superficie plana que está delimitada por la circunferencia.
Ya que tienes estas ideas acerca de algunos elementos del círculo, puedes realizar unas comprobaciones que te sugiere el desafío número 66 llamado “Conoces a Pi”, en la página 125
https://libros.conaliteg.gob.mx/20/P6DMA.htm?#page/125

Revisa qué vas a necesitar para contestar este desafío. Necesitas materiales de casa con forma de círculo, puede ser un reloj, unos aros. En total necesitas cinco objetos para llevar a cabo este trabajo, además de un hilo, lazo delgado o listón.
Ya con el material ahora lee la consigna, dice así:
En equipos lleven a cabo la siguiente actividad y después contesten lo que se pide. Utilicen hilo o cuerda para medir la circunferencia y el diámetro de los objetos que tienen en su mesa y registren sus resultados en la tabla, después obtengan sus cocientes y completen la tabla; pueden usar calculadora. Escriban sólo dos cifras decimales para expresar el cociente.
Ahora observa la información de la primera columna y anota el objeto que tengas, por ejemplo un aro chico, aro mediano, aro grande, plato chico y plato grande.

En la segunda columna dice: “Medida de la circunferencia”. Para obtenerla necesitas el listón o estambre y un metro o regla dependiendo del tamaño de los objetos.
Comienza con el aro chico. Debes sobreponer el estambre alrededor de la circunferencia y posteriormente el tamaño que resulte debes sobreponerlo en el metro para obtener la medida.
En la tercera columna dice: “Medida de diámetro”. Para obtenerla debes sobrepone el estambre entre dos puntos de la circunferencia, pasando por el centro.
Ahora que ya cuentas con todas las medidas que te piden en las tres primeras columnas de la tabla, vas a contestar la cuarta columna, puedes usar la calculadora.
Comienza anotando el valor de la circunferencia del primer objeto y dividíendolo entre el valor de su diámetro.
En el primer caso debe haberte dado tres punto catorce, quince y más cifras, anota este resultado en la tabla y ve con el siguiente cálculo.
Notarás que en el segundo caso otra vez te da el mismo resultado.
Observa qué ocurre con los valores de los otros tres objetos.
También resulta lo mismo, ¿Qué pasa?
Este valor es el de “Pi” y es un valor constante al dividir la longitud de la circunferencia entre la medida del diámetro, siempre da el mismo cociente.
Te preguntarás si esto ocurre sin importar el tamaño de la circunferencia, la respuesta es que si. Sin importar el tamaño de la circunferencia, si divides ese valor entre el valor de su diámetro, siempre será tres veces más un poquito, pero ese poquito más es difícil de determinar cuánto es con exactitud, ese es un problema actual, determinar el valor exacto de “Pi”.
La letra “Pi” que se usa para representar al número “Pi” proviene de la palabra griega perímetro.

Hoy has aprendido cosas interesantes acerca del círculo y en particular del número “Pi”.
El reto de hoy:
Presenta a alguno de tus familiares cercanos el ejercicio que realizaste con el estambre para medir la circunferencia de varios objetos y muéstrale como siempre va a medir lo mismo, explícale por qué.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas
