Meses sin interés
Aprendizaje esperado: anticipación del número de cifras del cociente de una división con números naturales.
Énfasis: seleccionar el resultado exacto de divisiones de números naturales, haciendo uso de diversos procedimientos, sin utilizar el algoritmo.
¿Qué vamos a aprender?
Aprenderás a realizar divisiones de un total, en partes iguales, utilizando diversos procedimientos, sin utilizar el algoritmo.
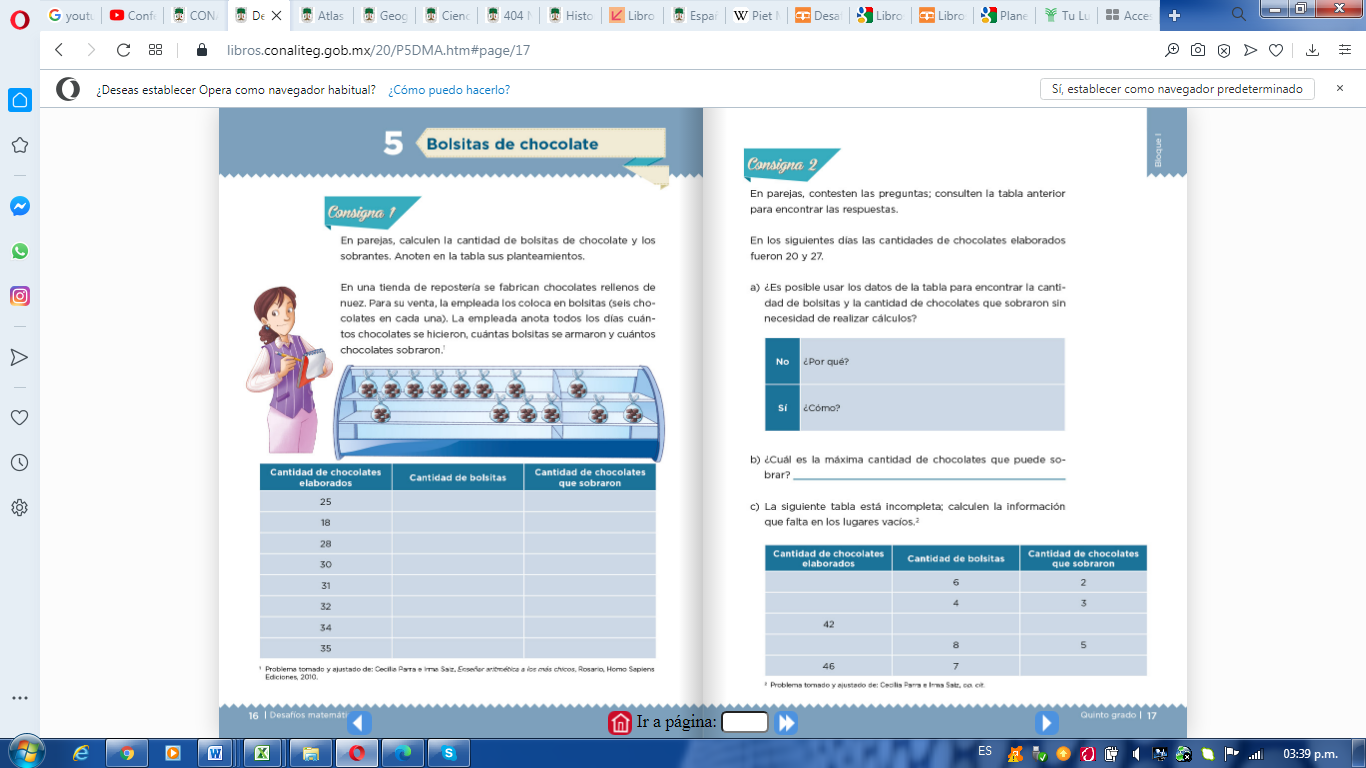
En tu libro de texto Desafíos Matemáticos. Quinto grado, podrás practicar este tema en la página 17
https://libros.conaliteg.gob.mx/20/P5DMA.htm?#page/17
Si no tienes el libro a la mano, no te preocupes, te anexo las actividades.
¿Qué hacemos?
Analizarás la siguiente situación.
Estoy interesado en comprar un celular para mis papás ya que en estos días no los he podido visitar por la emergencia sanitaria y de esta manera puedo tener comunicación todos los días con ellos.
Estoy interesado en comprarlo con un esquema de pago a meses sin intereses y he considerado pagar entre $ 500 y $ 600 pesos al mes, veamos cuál es la mejor opción.
¿Cómo consideras que se puede obtener el valor para pagar mensualmente?
Primeramente, debemos repartir la cantidad total entre el número de meses, veamos estas tres opciones:
- $7,800 a 6 meses sin intereses.
- $6,600 a 12 meses sin intereses.
- $7,020 a 9 meses sin intereses.

Vamos a realizar el cálculo para saber cuánto se pagará por mes.
Para el modelo A) que cuesta $7,800 vas a pagar $1,300 al mes durante 6 meses.
Sabes, ¿Cómo obtuve el resultado? hice agrupaciones de 1000 en 6, después los 1800 que sobraron los repartí de 100 en 100 entre los 6, obteniendo como mensualidad 1300, de la siguiente manera:
| Cantidad | Mes 1 | Mes 2 | Mes 3 | Mes 4 | Mes 5 | Mes 6 |
| 6000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 |
| 1800 | 100 | 100 | 100 | 100 | 100 | 100 |
| 100 | 100 | 100 | 100 | 100 | 100 | |
| 100 | 100 | 100 | 100 | 100 | 100 | |
| 7800 | 1300 | 1300 | 1300 | 1300 | 1300 | 1300 |
Para el modelo B) que cuesta $6,600, pagarías $ 1550 al mes durante 12 meses.
Para saber cuánto se pagará, busqué un número multiplicado por 12 que se acercará a 6000 multipliqué:
12×100 = 1200 le falta para 6000
12×200=2400 le falta para 6000
12×300=3600 le falta para 6000
12×4=4800 le falta para 6000
12×500=6000 le falta para 6000
12×700=7200 y se pasa de 6000
Entonces lo multipliqué por 500 y posteriormente un número multiplicado por 12 que se acercara a 600
12×10 = 120 le falta para 600
12×20=240 le falta para 600
12×30= 360 le falta para 600
12×4=480 le falta para 600
12×50=600, genial, justo lo que me faltaba. Por último, sume los dos números multiplicados por 12 que fueron 500 y 50 para obtener como resultado 550
Observa para obtener el resultado se realizó con el procedimiento siguiente:
Multiplicar 12×500=6000 después 12X50=600 y al finalizar sumar 500+50= 550
Para el modelo C) se pagarán 780 pesos mensuales durante 9 meses.
Para obtener el resultado, primero multipliqué 780×10 para ver el número aproximado, pero se pasa y después multipliqué 780×9 y obtuve el pago total de 7020, el procedimiento correcto es el siguiente:
780×10 = 7800 y 780×9=7020
Te explico, para dividir el total en partes iguales podemos emplear diferentes procedimientos:
- Para el modelo A) se utilizó la descomposición del número y posteriormente se repartió en partes iguales.
- Para el modelo B) se hicieron diferentes multiplicaciones para aproximarse primero a las unidades de millar y posteriormente a las centenas.
- Para el modelo C) se buscó un número multiplicado por el número de meses que se aproximará al total de la compra, en una división el total de la compra corresponde al dividendo, el número de meses al divisor y el pago mensual al cociente.
Ahora que ya sabes cómo calcular los meses sin intereses, lo podemos emplear para cuando realicemos una compra como pantallas, videojuegos, ropa, despensa.
El reto de hoy:
Resolverás el siguiente problema.
Juan va a comprar una computadora a 18 meses sin intereses que vale $21,600, ¿Cuánto va a pagar mensualmente?
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Consulta los libros de texto en la siguiente liga.