Los números y sus presentaciones
Los números y sus presentaciones
Aprendizaje esperado: relación de la escritura de los números con cifras y su nombre, a través de su descomposición aditiva.
Énfasis: usar el valor posicional de las cifras de un número para asociarlo a descomposiciones aditivas.
¿Qué vamos a aprender?
Aprenderás a usar el valor posicional de las cifras de un número para asociarlo a su descomposición.
¿Cómo te has sentido con las clases por televisión? ¿Te habías imaginado clases de esta forma? ¿Pensabas que las clases sólo podían ser dentro de una escuela?
A todo lo que sucede es importante ver la parte positiva, sin hacer a un lado lo negativo. Algo positivo del confinamiento por la pandemia del COVID-19 es que nos obligó a encontrar otras formas para que tú no pierdas clases.
¿Recuerdas cómo has compuesto y descompuesto números? y ¿Cómo has representado números de diferentes formas conservando la misma cantidad?
El día de hoy aprenderás a escribir cantidades, no sólo en cifras como lo hemos hecho hasta ahora sino también con letra, es decir, vas a lograr escribir el nombre de los números.
Sera interesante, pues así podrás darte cuenta de que existen diferencias entre escribir números con cifras y escribir su nombre, lo cual te ayuda a que no tengas errores cuando quieras representar una cantidad y que puedas manejarlas en diferentes situaciones.
¿Qué hacemos?
Observa con atención ejemplos de tres formas diferentes de representar una cantidad con unidades de millar.
- Observa la representación de las siguientes cantidades.
- 4535
Con letra se escribe:
Fíjate ahora cómo vamos transformando esta expresión escrita con palabras, en una expresión numérica separada en varias partes que sumaremos para obtener una sola.
¿Te das cuenta de que esta cantidad tiene todos los elementos de la descomposición en unidades, decenas, centenas y unidades de millar?
Al sumar todas estas partes:
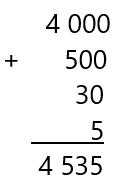
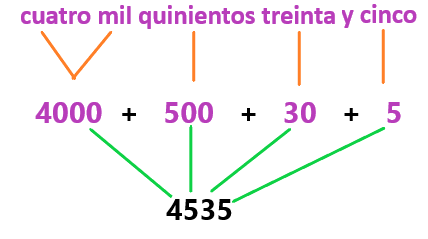
Te darás cuenta, que el número que se obtiene es el número 4535.
Es una buena forma para no equivocarnos cuando queremos escribir un número con cifras, ¿Verdad?
Intentemos con un nuevo número.
- 7078
Con letra ese escribe:
Estas palabras te dicen cómo se va a formar el número.
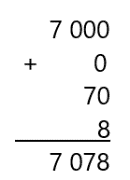Siete mil, más cero, más setenta, más ocho.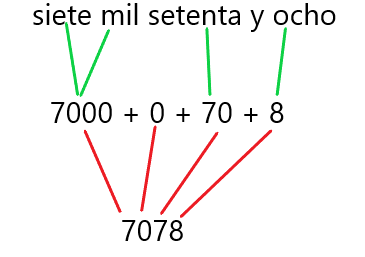
Al sumar todo esto tenemos 7078
De los dos ejemplos que acabas de observar, ¿Encuentras alguna diferencia?
Como puedes darte cuenta, en el número del primer ejemplo no hay ceros intermedios y en el segundo sí.
Dicho de otra forma, en el primer número hay miles, cienes o cientos, dieces y unidades a diferencia del segundo donde no hubo cienes o cientos.
Fíjate que hay muchas personas que tienen dificultades para saber cómo se escribe un número, sobre todo si ese número lleva ceros intermedios, con esta forma de pensar los números, pueden vencer esa dificultad.
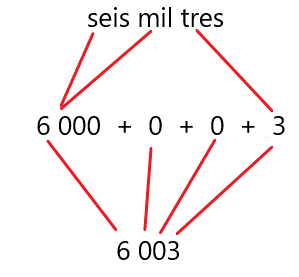
Vamos a hacer otros ejemplos, para que sigas practicando esta estrategia que se te propone. - 6003
Con letra se escribe.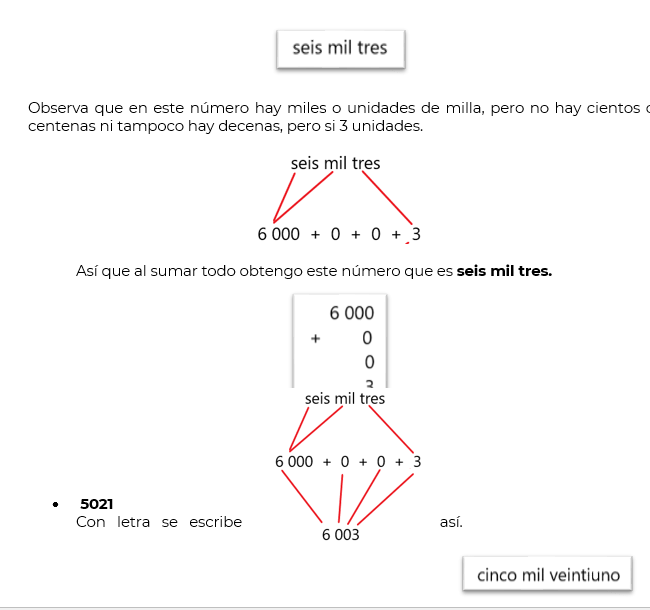
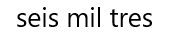
Observa que en este número hay miles o unidades de milla, pero no hay cientos o centenas ni tampoco hay decenas, pero si 3 unidades.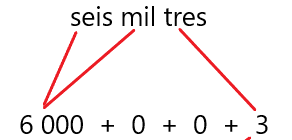
Así que al sumar todo obtengo este número que es seis mil tres.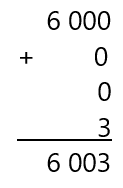
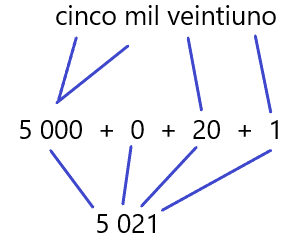
- 5021
Con letra se escribe así.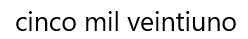
- Con notación desarrollada en unidades, decenas, centenas y unidades de millar, se escribe así.
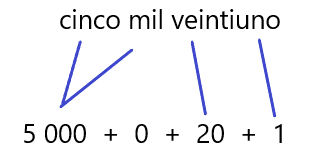
Miles o unidades de millar hay 5, no hay cientos o centenas, hay 20 decenas y hay una unidad.
Si realizamos esa suma nos permite encontrar la forma en que se representa esa cantidad con cifras.
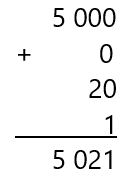
¿Tenías dificultades para escribir ciertos números?
Ojalá que estos ejemplos, te hayan ayudado a solucionarlas.
- Como siguiente actividad, te propongo realizar el juego de tu libro de Desafíos de la página 44.
¿Listo con tu libro en la página 44?
https://libros.conaliteg.gob.mx/P3DMA.htm?#page/44
En esta página se detallan las instrucciones del juego, y en las páginas 183 y 185 se encuentra el material recortable, que son las cartas de la baraja.
https://libros.conaliteg.gob.mx/P3DMA.htm?#page/183
https://libros.conaliteg.gob.mx/P3DMA.htm?#page/185
Para poder realizar esta actividad y hacerla más divertida, invita a tu mamá, papá, hermano o con a quien tu gustes a jugar.
Cuando tengas las tarjetas recortadas, agruparlas por color. También requerirás 20 tarjetas blancas en las cuales escribirás con letra, 20 cantidades que comprendan miles, una en cada tarjeta blanca.
Toma en cuenta lo siguiente:
- Son 5 colores de cartas, los cuatro de los recortables y las blancas.
- Los 5 grupos de cartas se colocan con los números hacia abajo.
- Cada jugador toma una carta de cada color.
- El número en la carta blanca está escrito con palabras y los jugadores deben formarlo con las cartas de colores que tienen en sus tarjetas de colores.
- Cada jugador, en su turno, devuelve al montón correspondiente, las cartas que no le son útiles, las coloca en la parte de abajo y toma de ese montón otra carta de la parte de arriba.
- El primero que forme el número de la carta blanca, gana la ronda.
- El que gane tres rondas, gana el juego.
Observa los siguientes casos para entender mejor la actividad.
PRIMERA TOMA DE CARTAS - El primer jugador toma sus cinco cartas de colores, en la blanca está escrito Tres mil trescientos cincuenta y tres y en las otras cuatro cartas 6000, 300, 80 y 9 respectivamente.
Tres mil trescientos cincuenta y tres.
6000
9
80
300 3000300
- El segundo jugador toma las suyas y en su carta blanca está escrito el número cuatro mil ochocientos sesenta y siete y en el resto de las cartas 2000, 900, 60 y 4.
2000
Cuatro mil ochocientos sesenta y siete.
900
4
60
SEGUNDA TOMA DE CARTAS
- El primer jugador se quedó con la amarilla y cambio las otras tres, por lo que en su carta blanca tiene Tres mil trescientos cincuenta y tres y en el resto de las cartas 3000, 300, 70, 3.
3
70
300
3000
Tres mil trescientos cincuenta y tres.
- El segundo jugador se quedó con la amarilla y roja, cambio las otras dos; ahora tiene Cuatro mil ochocientos sesenta y siete en la carta blanca y 5000, 800, 60, 2 en el resto de las cartas.
Cuatro mil ochocientos sesenta y siete.
5000
2
60
800
TERCERA TOMA DE CARTAS
- El primer jugador cambio sólo la roja y ¡gano! formo la descomposición aditiva de la carta blanca.
Tres mil trescientos cincuenta y tres, 3000, 300, 50, 3.
3
50
300
3000
Tres mil trescientos cincuenta y tres
Así como el ejemplo, juega en casa. ¡A jugar, divertirse y aprender en familia!
En cada ronda revuelve las cartas y forma nuevamente los cinco montones. Recuerda que el primero que gane tres rondas, será el ganador.
¿Te gustó el juego?
Continuamos con las consignas del desafío, pasa a la siguiente página.
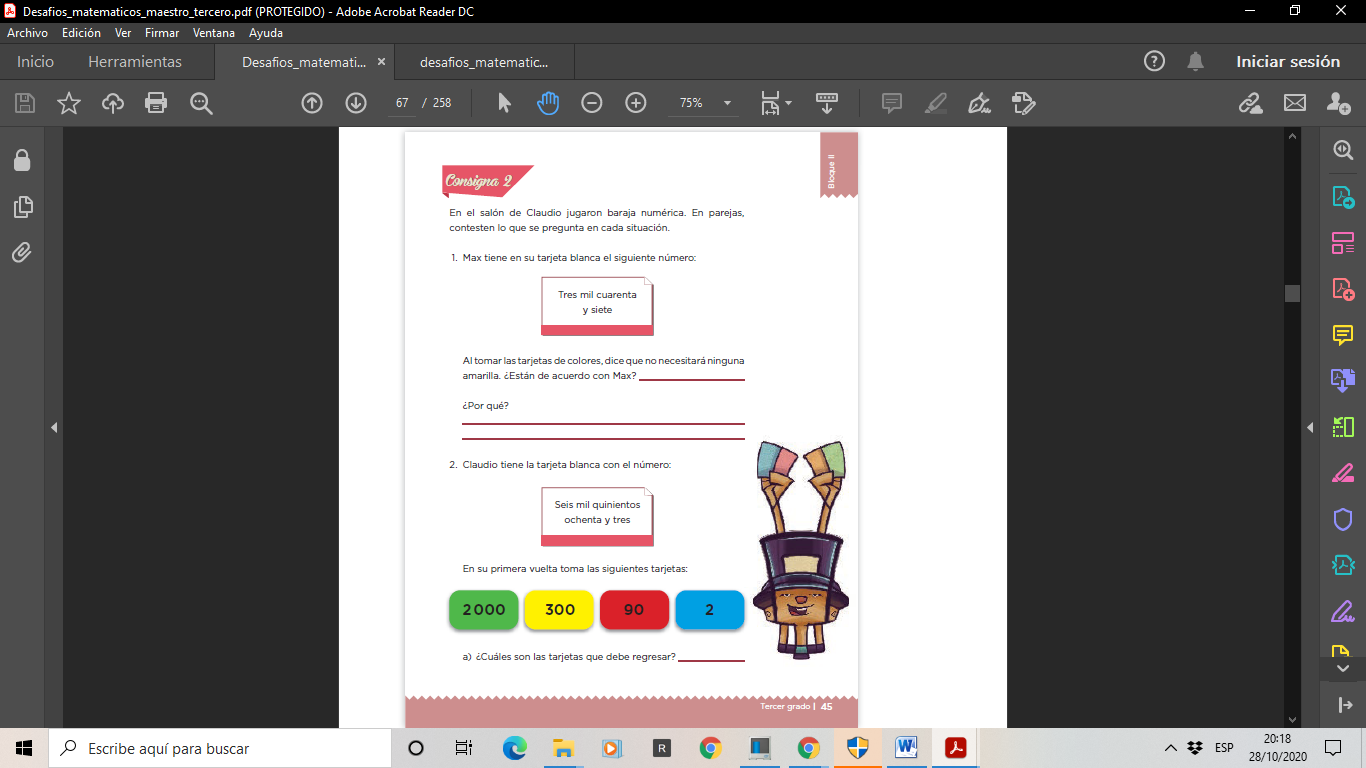
https://libros.conaliteg.gob.mx/P3DMA.htm?#page/45
Revisa la siguiente situación:
Nos platican que en el salón de Claudio jugaron baraja numérica, y realizan varias preguntas, vamos a responder la primera. Max tiene en su tarjeta blanca escrito esto:
Tres mil cuarenta y siete.
Al tomar las tarjetas de colores, dice que no necesitará ninguna amarilla. ¿Estás de acuerdo con Max? ¿Por qué?
En efecto, puedes estar de acuerdo con Max, porque tres mil cuarenta y siete, no tiene centenas. Su descomposición aditiva es: 3 000 + 40 + 7 y con cifras queda: 3047. En ambos casos se observa con claridad que no hay centenas y Max no necesitará tarjetas amarillas, que corresponden a las centenas.
Vamos con la segunda pregunta.
Claudio tiene la tarjeta blanca con el número:
Seis mil quinientos ochenta y tres.
En la primera vuelta toma las siguientes tarjetas:
2000
2
90
300
¿Cuáles son las tarjetas que debes regresar?
¡Bien! las tienes que regresar todas, porque ninguna te permite formar lo que dice la tarjeta blanca.
- Pero nos dice que en la segunda vuelta Claudio tomó estas tarjetas:
Por lo tanto, deberás regresar la verde y la azul, porque son las que no coinciden con el número de la tarjeta blanca. El quinientos y el ochenta sí coinciden, así que debe quedarse con ellas.
Observa y contesta, ¿Qué tarjetas le faltan para formar el número?
Si observaste bien, te darás cuenta de que le faltan las siguientes cartas:
Al final así quedaran sus tarjetas de colores para formar el número que dice la tarjeta blanca.80
Sigamos con la tercera pregunta.
Max ganó la última partida con estas tarjetas:
Al ganar la partida con estas tarjetas, podemos saber la cantidad escrita en la tarjeta blanca, la cual se escribe con cifra de la siguiente forma.4 118
¿Estás de acuerdo?
Ahora nos piden que se anote con letras.Cuatro mil ciento dieciocho
Así se lee y se escribe esa cantidad con letra.
Vamos con la última, la 4. - Al final del juego, los jugadores escribieron en una tabla los números que les tocaron. Completa la tabla de la página 46 de tu libro.
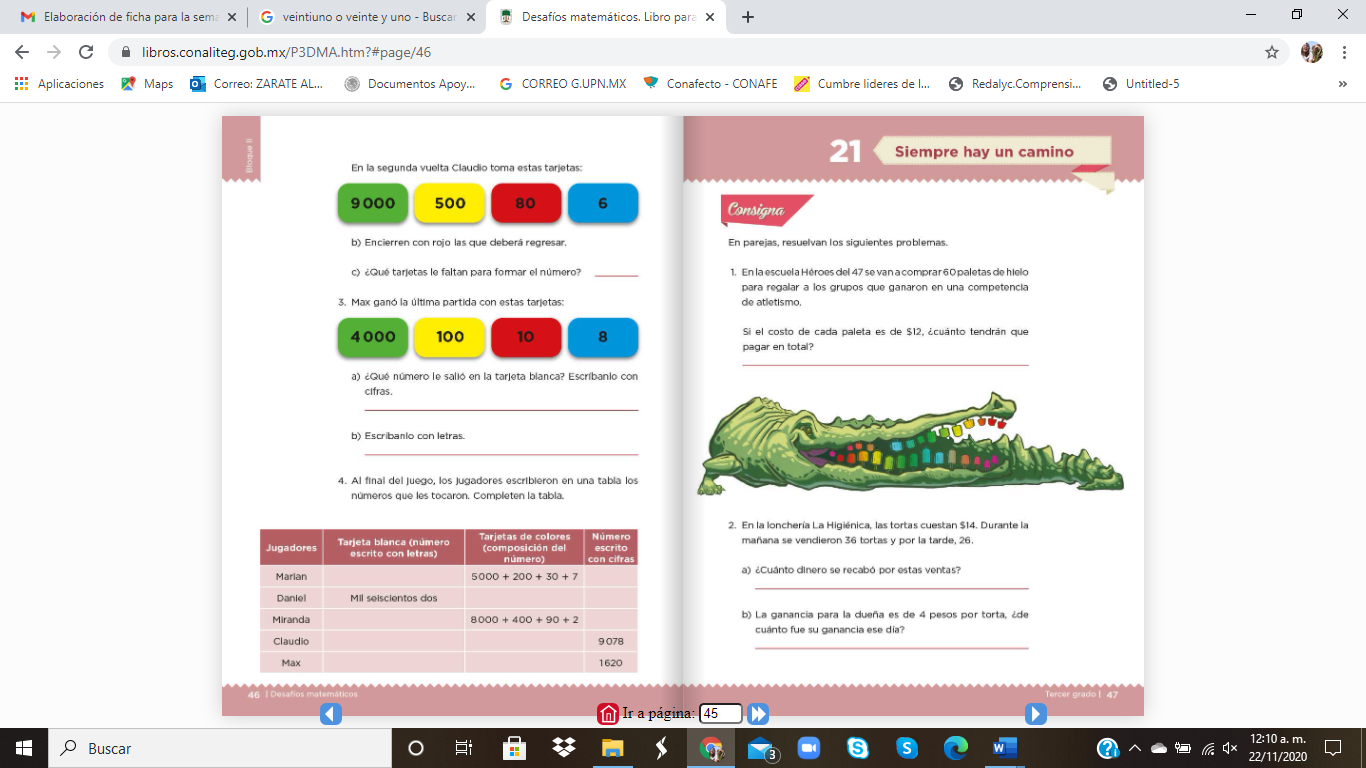
https://libros.conaliteg.gob.mx/P3DMA.htm?#page/46
Al llenar los espacios faltantes la tabla te quedará de la siguiente forma: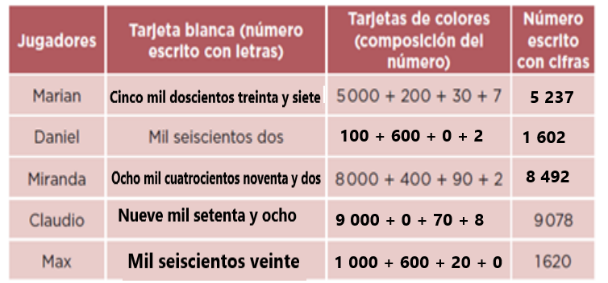
Revisa cuidadosamente la tabla anterior para que veas si aún tienes dudas y las puedas platicar a tu maestro o maestra.
Para reflexionar: - Recuerda que una cantidad cualquiera puede representarse con letra o con números, ya sea en su descomposición aditiva, o bien, con cifras.
- En la clase de hoy trabajaste con números de 4 cifras, lo que implica que está formado por unidades, decenas, centenas y unidades de millar, o unidades, dieces, cienes y miles, para que no se les olvide el valor de cada lugar.
- Cuando el número no cuenta con centenas, decenas o unidades, en su escritura con letra no se incluye y en su escritura con cifras se coloca cero en ese lugar.
Ejemplo:
Ocho mil cincuenta y ocho, no hay centenas, entonces con cifras queda 8 058.
Ocho mil cincuenta y ocho.
8 000 + 0 + 50 + 8
8 058
Continúa jugando con tu familia y sigue divirtiéndote con las matemáticas.
Si te es posible consulta otros libros, platica en familia lo que aprendiste, seguro les parecerá interesante y te podrán decir algo más.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas