¡Juguemos a la mercería!
¡Juguemos a la mercería!
Aprendizaje esperado: resuelve problemas de suma con números naturales menores que 100.
Énfasis: formar cantidades utilizando agrupamientos en decenas y unidades.
Descomponer cantidades de dos cifras en decenas y unidades.
¿Qué vamos a aprender?
Aprenderás a resolver problemas de suma con números naturales menores que 100
¿Qué hacemos?
Estoy muy emocionada porque cada día nos acercamos más al cierre de ciclo, además, estoy contenta porque durante un año he sido testigo de cómo has podido aprender nuevas cosas. ¿Qué fue lo que más te gustó?
A mi principalmente me gustó mucho la clase en donde observamos las distintas capacidades de contenedores e intentamos ponerles masa dentro, también disfruté mucho la clase en la que medimos las estaturas de las niñas y los niños.
¿Qué tema crees que fue el que más estudiamos?
El de las figuras geométricas, sin duda, ese fue un tema con el que trabajamos bastante.
Otro fue el de resolver problemas con operaciones de suma y resta.
A lo largo del ciclo escolar, has aprendido varias formas de resolver desafíos que implican sumar y restar. ¿Podrías mencionar algunas?
La del tablero de 100 la de los ficheros de 10 la de Ranalucía en la recta numérica.
Todas esas formas de sumar y restar utilizan el mismo método que es el de descomponer las cantidades en decenas y unidades. ¿Por qué crees que es más fácil sumar así?
Porque no tienes tantos dedos para hacerlo con las manos.
Sumar dos cantidades descompuestas en decenas y unidades, te permite hacerlo con los dedos, tomando en cuenta que cada dedo representa 10 unidades.
Jugar a sumar y restar porque todos los desafíos de clase se parecen mucho a los desafíos que se te presentan en la vida diaria.
Por eso pensé que es buena idea jugar a la mercería. ¿Qué te parece?
Ten preparado tu cuaderno en caso de que necesites escribir alguna idea, comentario o respuesta.
Para quienes no estén familiarizadas o familiarizados con esta palabra, la mercería es el lugar en donde se compran los botones, el estambre, las agujas y los hilos, entre muchas otras cosas más.
Yo seré la dueña de la mercería y tú el cliente.
Tú estás reparando algunas prendas y necesitas comprar botones.

Tienes 1 chamarra a la que le faltan 6 botones, un chaleco al que le faltan 4 un pantalón al que le falta 1 y una camisa que necesita 11 ¿Cuál es la operación que necesitas hacer para saber cuántos botones vas a comprar en total?
La palabra clave del desafío es “total” y te hace pensar que hay que sumar los números de botones de cada prenda.
La manera más fácil de sumar los botones es contándolos uno por uno. ¡Empieza a jugar!
Comienzan el juego.
- Buenas tardes, ¿En qué le puedo ayudar?
- Buenas tardes. Necesito comprar 6 botones negros, 4 cafés, 1 amarillo y 11 grises.
- Claro que sí, aquí tiene, en total, serían 22 botones.
- ¿Cuánto le debo?
- Cada botón cuesta 1 peso, me debe 22 pesos.
- Perfecto, aquí tiene, muchas gracias.
Le paga con dos monedas de 10 pesos y 2 de un peso terminan el juego.
Si observas las monedas con las que pagó. ¿Cuántos botones te puede pagar con la moneda de 10 pesos?
Esta moneda equivale a 10 monedas de 1 peso, o en este caso a 10 botones.
Por eso pago con 2 monedas de 10 pesos y 2 monedas de 1 peso.
Vas a hacer este mismo desafío un poquito más complejo. ¿Qué pasaría si el precio de los botones es distinto?
Entonces lo que debes de pagar no sería 22 pesos.
¿Regresa al juego para resolver un nuevo desafío?
Comienzan a jugar.
- Buenas tardes. Necesito comprar 6 botones negros, 4 cafés, 1 amarillo y 11 blancos.
- Claro que sí, aquí tiene, en total, serían 22 botones.
- ¿Cuánto le debo?
- Los botones negros cuestan 2 pesos, los cafés 10 los amarillos 5 y los blancos 1 peso.
Termina el juego.
No te preocupes si no sabes de inmediato. Recuerda que los desafíos se resuelven concentrándote, pero, sobre todo, con paciencia.
Vas a analizarlo. Los botones negros cuestan 2 pesos, los cafés 10, los amarillos 5 y los blancos 1 peso, tienes 6 botones negros, 4 cafés, 1 amarillo y 11 blancos.

Yo sugiero que primero calcules cuánto vas a pagar por cada grupo de botones y después sumes los totales.
¿Cuánto hay que pagar por los botones negros? ¿Qué estrategia puedes usar?
Podrías sumarlo con ayuda de tus dedos.
Vas a contar tus dedos cada botón que compres, pero cada uno tendrá un valor de 2, para contar de 2 en 2
Parece que es una buena forma de resolverlo. Recuerda que en otras ocasiones has contado con tus dedos dando un valor diferente a uno ya sea de 10 en 10 de 5 en 5 en esta ocasión lo harás contando de 2 en 2
Si son 6 botones tienes que contar seis veces 2
Llegas al 12 tienes que pagar 12 pesos por los botones negros.
El siguiente grupo de botones es el café y cuestan 10 pesos cada uno, ¿Cuánto tienes que pagar por 4 botones? 40
El siguiente número es muy fácil porque sólo es un botón y cuesta 5 pesos.
También los botones blancos porque, aunque son 11 valen 1 peso.
Entonces, ¿Cuánto hay que pagar por 11 botones? 11 pesos.
Vas a escribir los números en tu cuaderno, 12 + 40 + 5 + 11
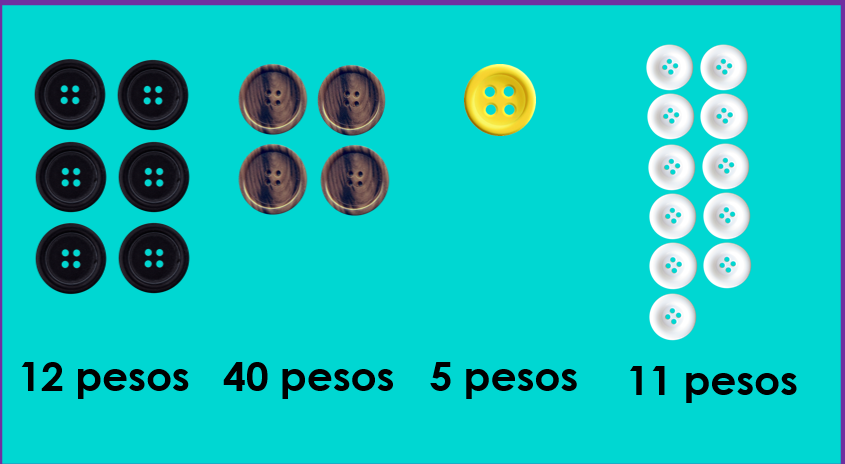
¿Qué estrategia puedes utilizar para saber cuánto dinero tienes que pagar por todos los botones?
Descomponer los números en decenas y unidades.
Primero comienza por las unidades para saber si puedes convertir las unidades a decenas, circula las unidades de cada número.

Sugiero que cuentes con los dedos. Pones el 2 en la cabeza y cuentas: 3, 4, 5, 6 y 7, más 1 son 8 no te alcanza para formar una decena.
Entonces guarda el 8 en la mente y ahora sumas las decenas.

Cuenta con los dedos. Pones el 1 en tu mente: 2, 3, 4 y 5. 5 más 1 son 6 pero ya no te acuerdas cuántas unidades habías contado.
Habías formado 8 unidades. 6 decenas más 8 unidades, ¿Cuánto es? 68
Entonces debe pagar 68 pesos.

Vas a hacer un último desafío dentro del mismo contexto.
¿Con qué otras combinaciones de monedas podrías pagar?
¿Puedes dibujar la tabla en tu cuaderno para que sepas si hiciste todas las combinaciones?
En la primera columna pones las decenas, en la segunda las unidades y en la tercera el total.
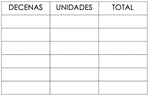
El total siempre debe dar 68
Podría pagar con 5 monedas de 10 y 18 monedas de 1 peso.
¿Qué otra combinación?
Con 4 decenas y 28 unidades. ¿Observas un patrón?
Las decenas de cada número van disminuyendo y las unidades aumentando.
¿Qué número crees que sigue?
En decenas el 3 luego el 2 y finalmente el 1
En unidades son saltos de 10 en 10 hacia adelante ya que sumas 38, 48, 58
¿Esas son todas las posibles maneras en las que puedes pagar?
Aún te queda una última forma de pagar.
También podría pagar sólo con 68 monedas de 1 peso.
Agrega ese número en la tabla.
¿Qué te pareció el juego de la mercería?
Te invito a jugar sumando cantidades utilizando el método de descomponer en decenas y unidades.
Recuerda que 10 unidades forman una decena y que es más práctico contar por decenas para dar saltos de 10 en 10 y no de 1 en 1 además de que en las manos no tienes 100 dedos, sólo tienes 10
Recuerda que es muy importante que vayas haciendo los ejercicios para que observes tus estrategias y resultados y los compares con los de la sesión.
Nos vemos mañana para la última sesión del ciclo escolar. ¡Qué emocionante!
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa*.
Para saber más:
Lecturas
