¿Es necesario el cero?
¿Es necesario el cero?
Aprendizaje esperado: ubicación de números naturales en la recta numérica a partir de la posición de otros dos.
Énfasis: advertir que, dada la escala por la ubicación de dos números cualesquiera en una recta numérica, no es indispensable ubicar el cero para representar otros números.
¿Qué vamos a aprender?
Aprenderás que, dada una escala por la ubicación de dos números cualesquiera en una recta numérica, no es indispensable ubicar el cero para representar otros números.
¿Qué hacemos?
Observa la siguiente situación.
“Rosaura pasea en su bicicleta en un parque que está en línea recta, y en su trayecto encuentra varios detalles que llaman su atención, entre ellos se da cuenta de que algunos metros que se señalaban en la pista, se han borrado”.
Observa el recorrido que hizo Rosaura.

¿Qué metros te muestra la recta de la pista?
Solo te indica la posición del 3 y del 7 ¿Y qué encontró Rosaura en el metro 5?
Para responder primero debes identificar cuántas unidades hay del 3 al 7.
Cuatro unidades: 4, 5, 6 y 7.
Entonces a la mitad de la distancia que hay entre el 3 y 7 está el 5. Por lo tanto, Rosaura encontró ahí un conejo.

Entonces, cada espacio de la recta indicado entre cada marca, ¿Cuántos metros representa? dos unidades o dos metros.
Entonces ya puedes contestar, ¿Qué vio Rosaura en el metro 11?

La línea que está adelante del 7 sería el número 9 ya que sumaste 7+2 = 9
Si continúas sumando tendrás que 9 + 2 = 11 por lo que el 11 está ubicado dos marcas adelante del 9.
Puedes concluir que en el metro 11 Rosaura observó a una ardilla.
También puedes ubicar el número 11, si a 7 sumas dos veces dos, es decir 4, de manera que los números 5 y 11 en la recta quedan ubicados de la siguiente manera.
Ahora tienes que Rosaura observó en otro de sus paseos lo siguiente.

Si observas el recorrido, sólo tiene dos números claramente escritos, así que, ¿Cuántas unidades hay del 17 al 29? 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29… ¡12 unidades!
Pero la recta está dividida en 6 partes iguales del 12 al 19.
Así que cada una de esas partes equivale a dos unidades, porque 12 números entre 6 segmentos nos da 2 números por segmento.
Entonces, ¿Qué vio Rosaura en el metro 13?

17 – 2 = 15 y 15 – 2 = 13 que serían dos marcas hacia la izquierda del 17, por lo que observó una mariposa.
¿Qué vio Rosaura en el metro 21?
17 + 2 = 19 y 19 + 2 = 21 que serían dos marcas a la derecha del 17. Tienes que observó un árbol.

Ahora, ¿Qué vio Rosaura en el metro 27?
Fácil, a 29 que está escrito, le resto 2, me da 27, que sería una línea antes del 29 y por lo tanto observó un tucán.
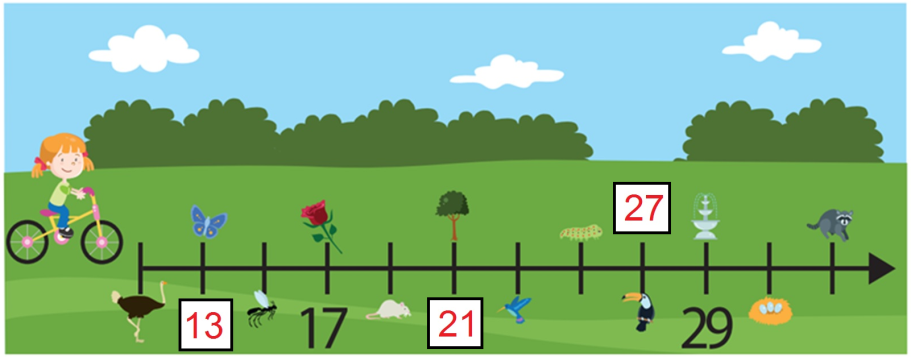
Por último, ¿Qué vio Rosaura en el metro 33?
29 + 2= 31 y 31 + 2 = 33 que serían dos marcas a la derecha del 29 y tienes que observó un mapache.
Ya tienes ubicados los números 13, 21, 27 y 33 en tu recta.
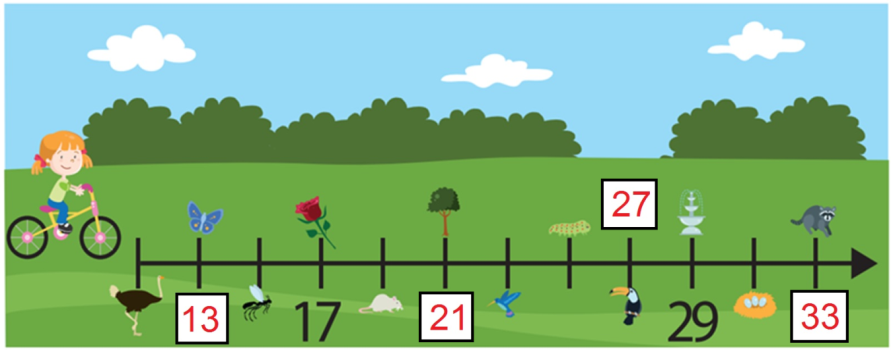
Ahora piensa, si para localizar números en un segmento de recta dado, ¿Fue necesario inicial el conteo desde el cero?
No fue necesario y este fue un ejemplo, lo que debes tener muy claro es cuántos números está abarcando cada segmento de recta y cuál es la distancia con la que tienes que graduar la recta.
Vas a desarrollar este proceso con un ejemplo. Si tienes un segmento de recta y en él se ubican dos números, por ejemplo, el 12 y el 18.
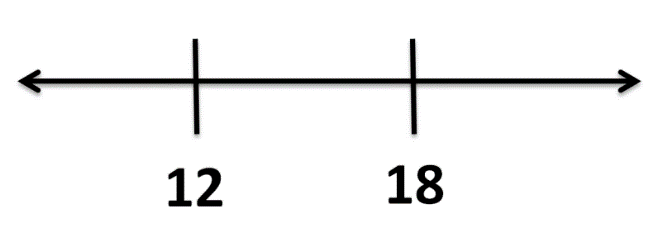
¿Qué debes hacer si quieres representar en la recta el número 15?
Debes identificar cuántos números está abarcando cada segmento de recta.
Bien, si cuentas cuántas unidades hay entre el 12 y el 18, tienes seis: 13, 14, 15, 16, 17 y 18, por lo que a la mitad de la distancia entre 12 y 7 hay 3 unidades.
Por lo tanto, el número que está a la mitad entre 12 y 18 es 15, ya que 12+3=15
Lo anterior se puede comprobar en la siguiente recta numérica.
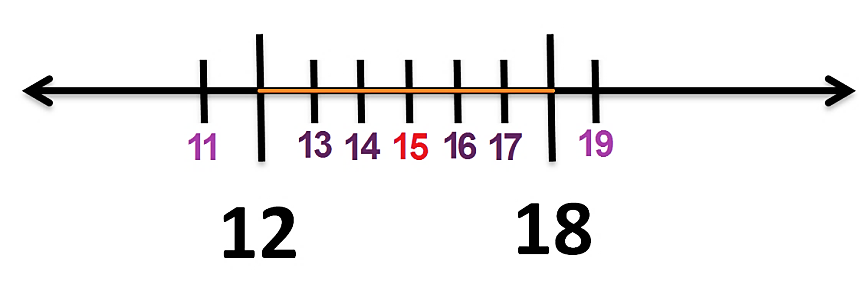
En este ejemplo, cómo puedes observar, conociendo la distancia de graduación de la recta se pueden identificar algunos otros números de forma ascendente, del 11 al 19 o descendente, del 19 al 11.
¿Cómo puedes marcar estas divisiones en la recta de forma apropiada?
Puedes emplear estambre o papel, aunque una mayor exactitud para medir los segmentos de recta se logra empleando la abertura de un compás o una regla; lo más idóneo es usar la regla, como lo viste en sesiones anteriores.
En la siguiente recta numérica vas a localizar los números 3 y 10, a partir de los números 4 y 8, que ya están ubicados en la recta.

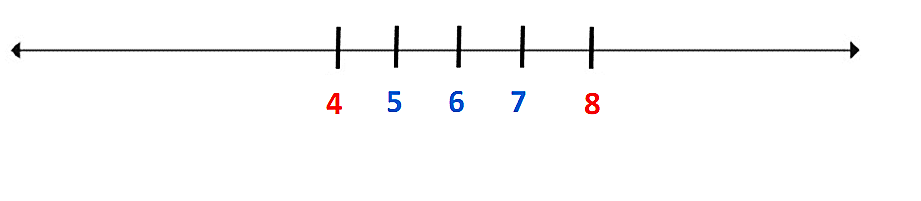
Analiza que del 4 al 8 hay cuatro unidades, por lo tanto, las indicaras al dividir en cuatro partes iguales entre segmento, así estableces la distancia que hay entre dos números naturales consecutivos sobre la recta.
Ahora, conociendo la distancia y las unidades consideradas en ella, puedes determinar el lugar donde se ubica el 3. Para ello seguimos esa medida a la izquierda.

Mide la misma distancia que hay del 4 al 5 pero a la izquierda del 4 y ubicas el 3.
Y, para ubicar el 10 necesitas seguir dos segmentos de recta a la derecha del 8.

Por lo que ya tienes representado los números 3 y 10 sobre la recta.
En la siguiente recta numérica vas a ubicar los números 19, 25 y 43.

Si estableces cuántas unidades hay del 27 al 35 tienes 8 unidades: 28, 29, 30, 31, 32, 33, 34 y 35. Por ello cada marca en la recta indica grupos de 8 números. Para ubicar a los números 19 y 43 deberás restar y sumar respectivamente 8.
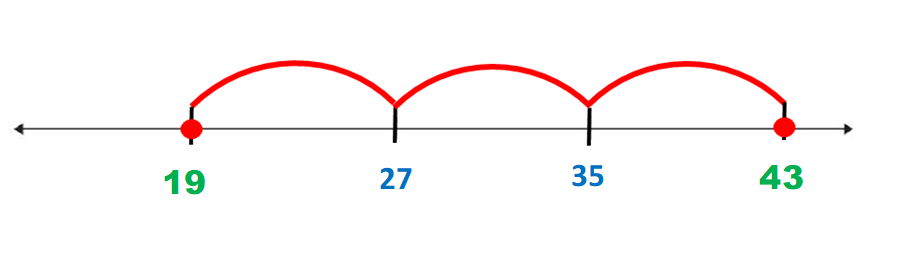
Primero ubicaras el 19 así que 27 – 8 = 19
Para ubicar el 43 sumaremos 35 + 8 = 43
Tomando en cuenta que del 19 al 27 hay ocho unidades, indicaría grupos de dos en dos unidades. Esta escala nos puede facilitar ubicar el número 25.
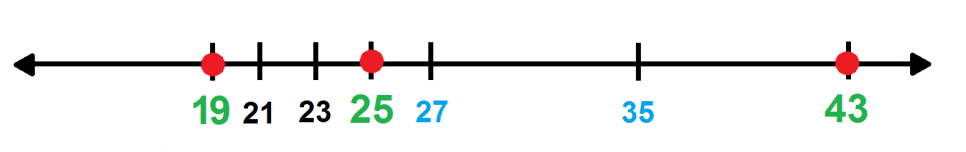
Claro, el 25 se encuentra entre el 19 y el 27, por lo que ese segmento lo puedes dividir en cuatro partes iguales. Anotas los números localizados en esas marcas y ubica al 25 y así es como quedan representados los tres números 19, 25 y 43, respectivamente
Pudiera parecer difícil, porque no aparece el 0, pero ya al realizar el ejercicio como se explicó, no cabe duda que no es necesario marcarlo sobre la recta; siempre y cuando tengas claro el procedimiento y lo sigas adecuadamente. Es importante destacar que no existe una sola manera de realizar el proceso de ubicación de cada uno de los números.
Una respuesta distinta del ejercicio que acabas de finalizar. Vas a ver cómo lo resolvió este alumno de Hidalgo que con mucho entusiasmo concluyó y compartio su procedimiento.
Dice que para representar en la recta los números 19, 25 y 43 hizo lo siguiente:

Como hay 8 unidades de 27 a 35 lo primero que hizo fue ubicar el 19 a la izquierda del 27, marcando un segmento de 8 unidades, porque si a 27 le resto 8 me da 19.
En seguida ubiqué el 25, creando a la izquierda del 27 dos segmentos de dos unidades, considerando que, si a 27 le quito dos, me da 25.

Y por último ubiqué el 43, estableciendo un segmento de ocho unidades a la derecha a partir del 35. Porque si a 35 le sumo 8 me da 43.

Su proceso de ubicación de cada uno de los números fue más directo.
Realiza un último ejercicio para continuar aprendiendo.
En la siguiente recta vamos a ubicar los números 36 y 51 a partir de tres números que se ubican en el segmento de recta.

Tienes marcada la distancia entre dos unidades consecutivas, de manera que, si adelante del 40 ubicas el 41 y comparas las distancias que hay del 40 al 45 y del 41 al 46, estas distancias son iguales porque entre las dos parejas de números hay una diferencia de 5 unidades.
40 + 5 = 45
41 + 5 = 46
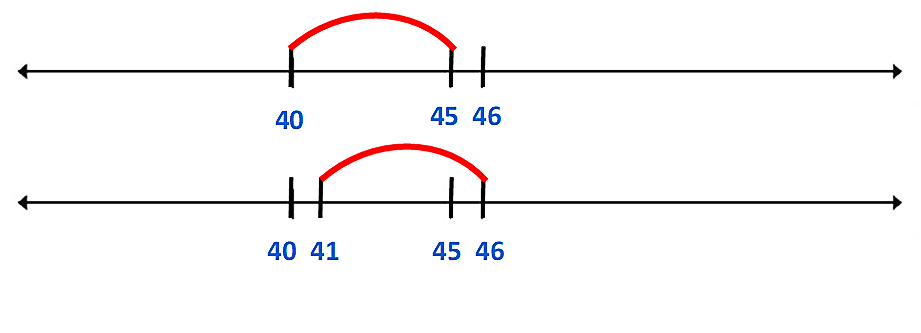
Si marcas en la recta las distancias iguales, te queda algo así.
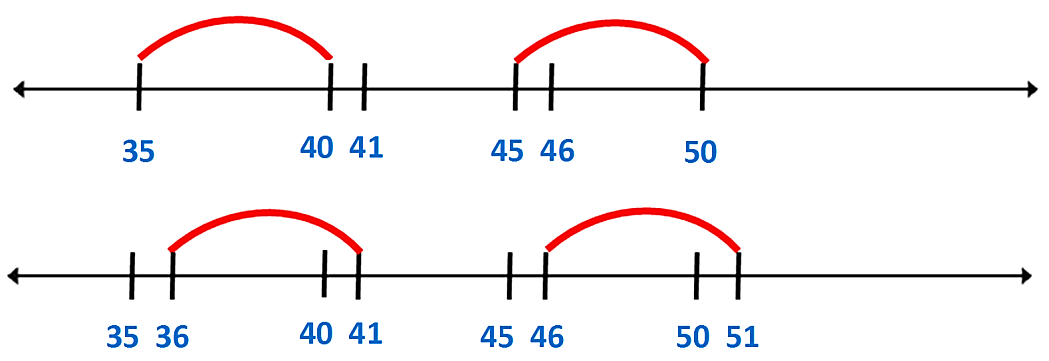
Ahora realizarás la misma acción para ubicar los números 36 y 51. Tomando en cuenta que la diferencia entre 35 y 40 y entre 45 y 50 es respectivamente de cinco números.

Y ahora ya puedes señalar la ubicación del 36 y del 51.
Recuerda que en este tipo de ejercicios debes primeramente identificar la escala que está determinada tanto por la distancia existente entre dos números indicados en la recta como por los números considerados en ese segmento de recta.
En este ejercicio la escala se determinó por segmentos de recta de 5 unidades, comprendidos entre los números 40 al 45 y por el consecutivo entre 45 y el 46.
Con este ejercicio has terminado esta sesión, recapitulando lo aprendido:
- La escala está determinada por la distancia existente entre dos números cualesquiera no necesariamente consecutivos en la recta y el conjunto de números que esa distancia agrupa.
- La graduación en la recta numérica debe respetar la distancia que se ha medido entre los números establecidos, para ubicar cualquier otro número sobre la recta.
- La ubicación del cero en la recta no es un requisito para ubicar otro número.
El reto de hoy:
Resuelve el desafío de tu libro de texto de Desafíos matemáticos de la página 49.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
