¿Es necesario el cero? II
¿Es necesario el cero? II
Aprendizaje esperado: ubicación de números naturales en la recta numérica a partir de la posición de otros dos.
Énfasis: advertir que, dada la escala por la ubicación de dos números cualesquiera en una recta numérica, no es indispensable ubicar el cero para representar otros números.
¿Qué vamos a aprender?
Continuarás aprendiendo que, dada la escala por la ubicación de dos números cualesquiera en una recta numérica, no es indispensable ubicar el cero para representar otros números.
¿Qué hacemos?
Planteamiento de la situación:
“Rosaura recorre otro tramo de la pista. En el metro 55 se encuentra una tortuga, en el 70 una rana y en el 85 una guacamaya, ¿Cómo podrías ubicar el lugar donde encontró a la tortuga, a la rana y a la guacamaya en el recorrido?”
Si tienes como referencia la siguiente recta para representar el recorrido.
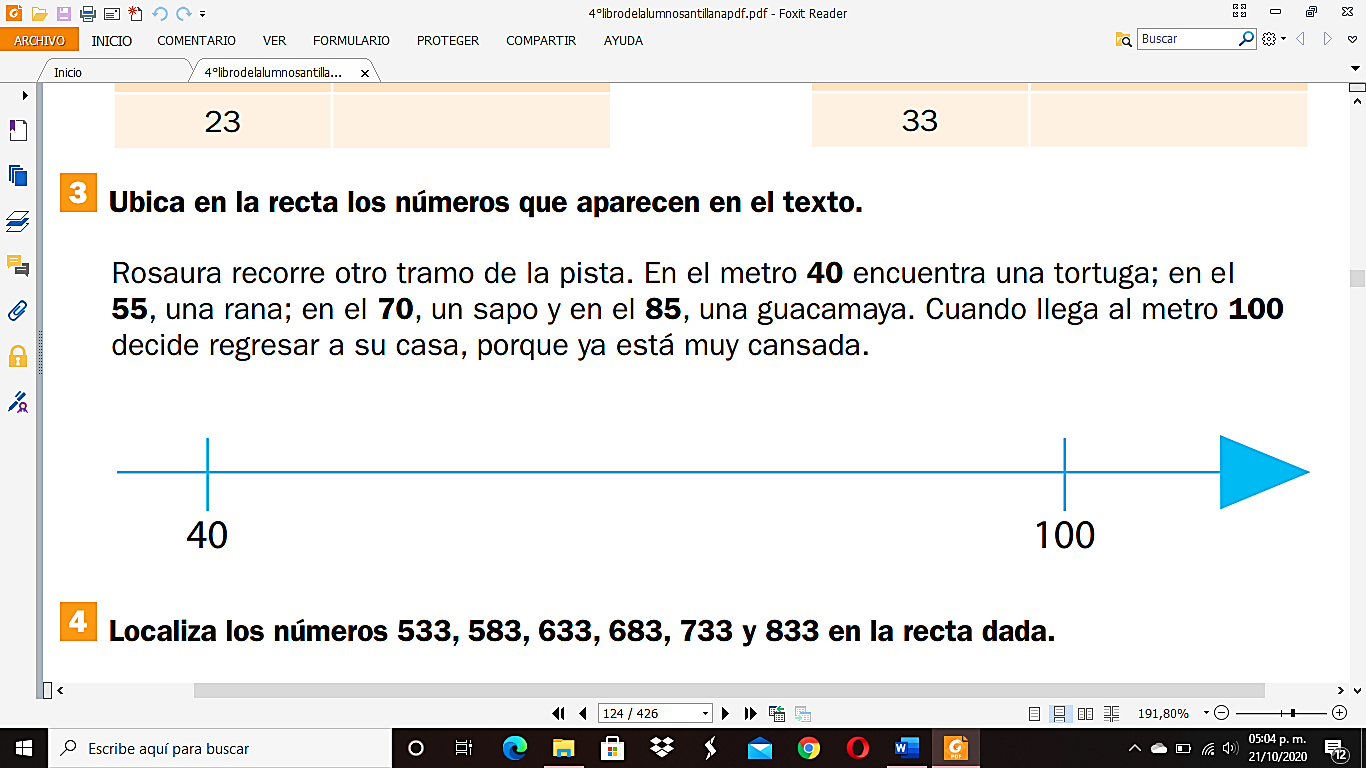
¿Cómo podrías ubicar el lugar donde encontró la tortuga, a la rana y a la guacamaya?
Primero tendrás que identificar la escala que te dan estos dos valores, 40 y 100.
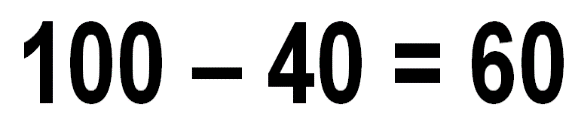
Si realizas una simple resta de 100 – 40 = 60 obtienes que hay 60 unidades entre estos dos valores.
Ahora analiza los números a representar 55, 70, 85 ¿Tienen algo en común?
Sí, son parte de una serie que se desarrolla de 5 en 5. Entonces si en la recta observas que del 40 al 100 hay 60 unidades, podrías dividir ese segmento en 6 partes iguales para obtener 6 nuevos segmentos de recta que representen 10 unidades cada uno, quedando así.

Ahora ya podrías representar en la recta el metro 70, que es donde vio a la rana.

El metro 70 se ubica en la tercera marca del segmento de recta a la derecha del 40 o, lo que es igual, a la mitad de la distancia existente entre 40 y 100.
Y ahora, ¿Cómo puedes ubicar al metro 55?
Ya sabes que los segmentos en que dividimos la recta valen 10 unidades, sólo tendrías que volver a dividir cualquier segmento para representar el número intermedio, cinco, entre ambas cantidades, es decir, que para representar el 55 tendrías que dividir a la mitad el segmento que está entre las marcas que indican el 50 y el 60, quedando así:
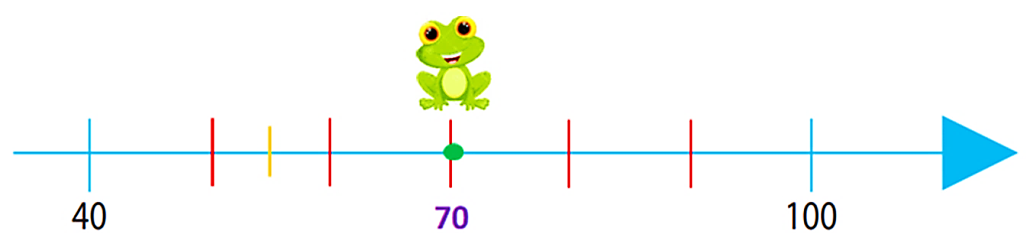
Entonces ya puedes representar en la recta el metro 55, que es donde Rosaura vio una tortuga.
Por último, ¿Cómo ubicas al metro 85?

Si recurres al procedimiento anterior, tendrás que dividir el segmento que está indicado entre las dos marcas que señala el 80 y 3l, 90 en dos partes iguales. Recuerda que hay que emplear la regla para hacer de manera exacta la división y queda así.

Ya puedes representar en tu recta el metro 85, que es donde vio a una guacamaya.

¿Será necesario indicar el cero para localizar números naturales en una recta dada? No, ¿Verdad? este ejemplo deja claro que sin ubicar el cero es posible situar cualquier número, conociendo la escala entre dos de ellos, la cual se define por la distancia entre dos números conocidos que pueden ser no consecutivos y la cantidad de números que esa distancia agrupa.
Aplica el procedimiento para ubicar cualquier número en la recta en otro ejemplo.
Como te diste cuenta el día de ayer ubicaste en la recta números menores a 50.
El día de hoy trabajarás con números hasta el 100. Comencemos recordando que primero se debe identificar cómo se dividió la recta. Posteriormente hay que identificar el rango de números que agrupa cada espacio entre marcas.

Como puedes observar, la recta tiene indicados los números 62 y 78 pero, ¿Qué debes hacer si quieres representar en la recta el numero 66 por ejemplo?
Entre el 62 y el 78 hay 16 unidades, ¿Cómo lo sabes? realizando una resta de los números indicados en la recta: 78 – 62 = 16
Tienes que dividir este segmento en 2 y 4 partes iguales, las cuales son equivalentes a 8 y 4 unidades respectivamente, ya que 2 x 8 = 16 y 4 x 4 = 16
Por tanto, el número que estaría a la derecha del 62 seria 66, ya que 62 + 4 = 66
Lo anterior te lleva a la siguiente recta numérica.
Aquí estás aplicando lo que has aprendido.

Realiza otro ejercicio.
Aquí tienes otra recta numérica, en ella vas a ubicar un par de números, el 30 y el 100, a partir de la ubicación del 40 y el 80 que están en la recta.

Entre el número 40 y el número 80 hay 40 unidades. Por lo tanto, la distancia que hay entre 40 y 80 la puedes dividir de formas distintas, por ejemplo, en cuatro partes iguales para definir una escala de 10 unidades entre cada marca.

Habiendo establecido una escala de 10 en 10 puedes determinar el lugar donde se ubica el 30.
Para ello, marcarás un segmento de 10 unidades a la izquierda del 40 y ubica al 30, ya que 40 – 10 = 30

Para ubicar el 100, necesitas dos segmentos de recta de 10 unidades que marcarás a la derecha del 80.

Así tienes ubicados los números 30 y 100 sobre la recta.
Pasa a otro ejercicio.
Los números que vas a ubicar en la recta son el 49, el 55 y el 73.

Entre los números 57 y 65, existe una relación numérica, una diferencia de 8 unidades, y si cuentas verán que también entre los números 49, 57, 65 y 73, que intervienen en este ejercicio, se presenta la misma relación.

Eso quiere decir que la distancia que hay entre todos estos números es igual a 8 unidades.
La distancia que existe entre 57 y 65 la vas a estirar o repetir a la izquierda del 57, para ubicar el 49 y a la derecha del 65 para ubicar el 73.
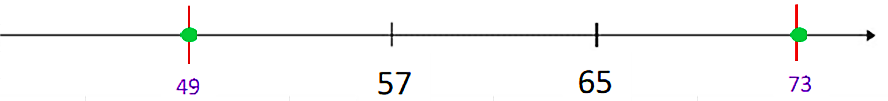
Entonces que del 49 al 57 hay ocho unidades. Esta distancia la puedes dividir en cuatro partes para marcar conteo de dos en dos y puedas ubicar el número 55 sobre la recta.
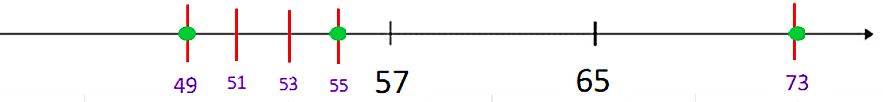
Así es como quedan representados los tres números: 49, 55 y 73, respectivamente.
Es importante que recuerdes que no existe una sola manera de lograr la ubicación de números naturales en la recta, ya que existen varias formas de llevarlo a cabo dependiendo del rango de números que indiquemos con las particiones que hagas sobre ella.
Vas a realizar un último ejercicio.
En la siguiente recta vas a ubicar los números 86 y 101 a partir de tres datos.

Observa que tienes indicada la distancia entre dos números consecutivos, 95 y 96. Si a la derecha del 90 repites esa distancia, puedes localizar el número 91.
Si comparas las distancias que hay del 90 al 95 y del 91 al 96, estas distancias son iguales, porque entre ambas parejas de números hay una diferencia de 5 unidades.

Y si marcas en la recta las distancias iguales, te queda así.

Realizarás la misma acción para ubicar los números 86 y 101 ya que la diferencia entre 85 y 90 y entre 95 y 100 también es de cinco números.

Ya puedes señalar la ubicación del 86 y del 101 sobre la recta.
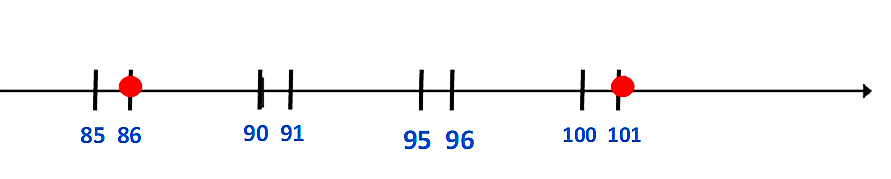
Con este ejercicio has concluido esta sesión.
Para enfatizar lo que aprendiste hoy.
- La escala está determinada por la distancia existente entre dos números cualesquiera no necesariamente consecutivos en la recta, y el conjunto de números que esa distancia agrupa.
- La graduación en la recta numérica debe respetar la distancia que se ha medido entre los números establecidos, para ubicar cualquier otro número sobre la recta.
- La ubicación del cero en la recta no es un requisito para ubicar otro número.
El reto de hoy:

¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
