El viaje
El viaje
Aprendizaje esperado: resuelve problemas en los que sea necesaria la conversión entre los múltiplos y submúltiplos del metro, del litro y del kilogramo.
Énfasis: establece relaciones de equivalencia entre las diferentes unidades de medida de longitud y realiza conversiones para resolver problemas.
¿Qué vamos a aprender?
Aprenderás a resolver problemas en los que sea necesaria la conversión entre los múltiplos y submúltiplos del metro, del litro y del kilogramo.
¿Qué hacemos?
Para iniciar la sesión de hoy, te comento que Angélica, Jaqueline y Josué son 3 amigos que se quieren ir de vacaciones a distintos puntos turísticos dentro de nuestro país, después de que termine la pandemia, ellos tienen 3 destinos turísticos y acá está la pregunta que les acongoja: quieren saber, ¿Cuál de ellos es el más cercano para poder visitarlo?
Cada uno de ellos tiene una unidad de medida de longitud totalmente distinta, kilómetros, hectómetros y decámetros y nos piden ayuda para saber quién se encuentra más cerca de la Ciudad de México.
Pon mucha atención, vamos a desglosar este asunto.
Lo primero que vamos a hacer es recordar con la escala de medidas como se transforma.
Para transformar de una unidad chica a una grande, se tiene que dividir entre 10 y si es de una unidad grande a una chica, se multiplica por 10
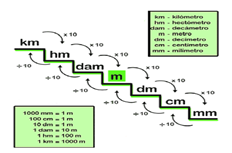
Te recuerdo esto, porque debemos tener en la misma unidad las distancias para poder compararlas.
El metro es la unidad base que se emplea para medir longitudes y a partir de él se forman otras unidades de medida, tanto mayores llamadas múltiplos, como más pequeñas, llamadas submúltiplos.
El metro es una unidad de medida que pertenece al sistema internacional de unidades. La palabra metro viene del griego metron, que significa “medida” y los nombres de estas unidades se forman por prefijos griegos seguidos de la palabra griego.
Deca. significa diez veces.
Hecto. significa cien veces.
Kilo. significa mil veces.
Deci. significa una décima parte.
Centi. significa una centésima parte.
Mili. significa una milésima parte.
La unidad principal de longitud y distancias es el metro y todas las demás están relacionadas con él.
Observa ya tenemos la equivalencia en metros de todas estas unidades.
Mil milímetros es igual a un metro.
Cien centímetros es igual a un metro.
Diez decímetros es igual un metro.
Un decámetro son diez metros.
Un hectómetro son cien metros.
Un kilómetro son mil metros.
Para conocer un poco más de los lugares que quieren visitar Angélica, Jaqueline y Josué, nos enviaron un pequeño video, te invito a observarlos.
Jaqueline quiere visitar Puebla porque le recomendaron ese sitio sus tíos, observa el video del segundo 00:36 al 00:53
- Los once más de Puebla.
https://youtu.be/jBmb2G7H4fo?t=36
Angélica le encantaría visitar Hidalgo, porque nos comenta que hay paisajes bellísimos, observa el video del segundo 00:08 al 00:29 - Los once más de Hidalgo.
https://youtu.be/yYKOWDJqH_I?t=8
Josué quiere ir a Morelos, observa el video del segundo 00:36 al 00:57 - Los once más de Morelos.
https://youtu.be/1WnHzRPIIqQ?t=36
Son fantásticos los lugares de nuestro país, es extraordinaria la variedad que encontramos en nuestro México Lindo y Querido.
Angélica nos comentó que está a nueve mil decámetros de Hidalgo, Jaqueline quiere visitar Puebla que está a mil trescientos cincuenta hectómetros y por último Josué quiere ir a Morelos que está a ciento veinte kilómetros.
Hagamos las conversiones de cada uno a metros para poder ver quién es el que tiene la propuesta para ir más cerca del centro de la Ciudad de México.
Primero vemos todas las conversiones a metros.
El decámetro vale diez metros.
El hectómetro cien metros.
El kilómetro mil metros.
El metro es la unidad principal.
El decímetro cero punto un metros.
El centímetro cero punto, cero un metros y el milímetro cero punto cero, cero un metros.
Es momento de ayudar a nuestros compañeros, ya tenemos más claro cómo los podemos apoyar.
Vamos uno por uno para poder hacer la conversión de las distancias.
El de Angélica que es de la ciudad de México hasta Hidalgo y son nueve mil decámetros.
9 000 dm x 10 = 90 000 m.
A los nueve mil vamos a multiplicarlos por diez para obtener su equivalencia en metros y nos da como resultado noventa mil metros.
Eso quiere decir que la distancia total en metros es noventa mil.
Ahora vamos con Jaqueline. Ella, quiere ir a Puebla y son mil trescientos cincuenta hectómetros.
1 350 hm x 100, multiplicamos por 100, porque un hectómetro tiene 100 metros, 1350 hm = 135 000 m.
Este número es mucho más grande que el anterior, eso quiere decir que Angélica va ganando con la distancia más corta.
Vamos por el último para saber quién de los tres amigos es el que tiene menos recorrido. Es el de Josué que quiere ir a Morelos y son ciento veinte kilómetros.
120 km x 1000.
A estos ciento veinte kilómetros lo vamos a multiplicar por mil que es su equivalencia en metros y nos va a dar como resultado 120 km = 120 000 m.
Ahora sí podemos ver que es Angélica la que va más cerca de la Ciudad de México.
Como en esta situación, con las conversiones entre múltiplos y submúltiplos del metro, vamos a poder determinar que distancia es la mayor, o la menor.
¿Qué pasa si en los kilómetros, hectómetros o los decámetros, encontramos una fracción?
R = De igual manera sólo vamos a multiplicarlo por diez, cien o mil, según corresponda o el otro método más fácil, ir recorriendo el punto decimal y agregando ceros, según sea el número por el que desees transformar.
Para que te quede más claro, vamos a resolver la consigna 3, del desafío número 72 “Equivalencias” que se encuentra en la página 138 de tu libro de Desafíos Matemáticos.
https://libros.conaliteg.gob.mx/20/P5DMA.htm#page/138
El primer problema dice:
- Eleazar camina todos los días de su casa a la escuela 1 kilómetros. Si cuando pasa por la tienda lleva recorridos 320 metros, ¿Cuánto tiene que recorrer todavía para llegar a la escuela?
Vamos por partes, la primera es, ¿a cuántos metros equivale 1 km?
R = Mil quinientos metros.
Lo primero que vamos a hacer es convertir todo a metros, primero 1 kilómetro es igual a mil metros, y medio kilómetro, dividimos mil entre dos y sólo tomamos la mitad que son quinientos metros.
Nos da un resultado total de mil quinientos metros y ahora sólo restamos mil quinientos menos trescientos veinte y nos da como resultado mil 180 metros.
R = Eleazar tiene que recorrer 1 180 metros para llegar a la escuela.
Vamos a resolver el siguiente problema: - A un trabajador del municipio le encargaron pintar las guarniciones de las banquetas, tiene que pintar 8 calles y cada una mide 1 hm, hasta el momento lleva 245 metros pintados, ¿Cuántos metros le faltan por pintar?
Seguimos con los mismos pasos, primero vamos a convertir los hectómetros a metros. En este primero tenemos que ver que las 8 calles miden 8 hectómetros, pues cada una mide un hectómetro, luego serían las ocho calles por cien que mide cada hectómetro y el resultado es ochocientos metros.
Ahora toca restar, si a ochocientos le quito doscientos cuarenta y cinco el resultado es 555 metros.
R = Al trabajador le faltan 555 metros por pintar.
El tercer problema dice: - Un caracol se desplaza sobre una jardinera que mide 2 metros de largo, si recorre 13 mm por segundo, ¿Cuántos segundos necesita para recorrer el largo de la jardinera?
En este caso sugiero que convirtamos los 2 metros en milímetros y serían entonces dos mil milímetros, dividimos los dos mil entre trece para saber cuántos segundos se va a tardar y el resultado es 153 segundos y 84 centésimas de segundo.
R = El caracol necesita 153.84 segundos para recorrer el largo de la jardinera.
Con las matemáticas, podemos resolver muchos problemas, como el que tenían Angélica Jacqueline y Josué.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
