El acertijo
El acertijo
Aprendizaje esperado: resolución, con procedimientos informales, de sumas o restas de fracciones con diferente denominador en casos sencillos (medios, cuartos, tercios, etcétera).
Énfasis: resuelve problemas que impliquen sumar o restar fracciones mediante diversos procedimientos.
¿Qué vamos a aprender?
Aprenderás sobre fracciones comunes.
¿Qué hacemos?
Seguramente te ha pasado alguna vez que has querido seguir alguna receta te has encontrado con algunos problemas para hacerlo, intenta resolver el siguiente problema que le sucedió a una persona, léelo con atención.
Fui muy temprano a la central de abastos y compré todo lo que requería para un caldo de pollo: 1 kilogramo de papa, 1 kilogramo de calabaza, medio kilogramo de chayote, medio de zanahoria; en casa tenía ¾ kg de pollo, cuando venía de camino compré en la carnicería ½ kg más. Pero me he dado cuenta de que la receta dice que se necesitan 2 kg de pollo en total. ¿Cuánto pollo me falta comprar?
¿Qué es lo primero que tienes que hacer? ¿Qué se te ocurre?
Una manera podría ser calcular el total de pollo que ya se tiene, para después sacar la diferencia con los 2 kilogramos que dice la receta.
Para lograr resolverlo vas a utilizar una forma muy sencilla de sumar fracciones, tienes que obtener una fracción equivalente, como se dibuja en la siguiente representación, ½ debe ser convertido a cuartos para poder hacer la suma con los ¾
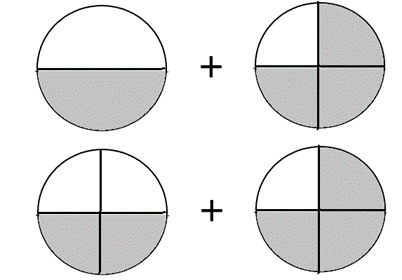
¿Ya lo recordaste? Esto ya lo habías hecho en clases anteriores, así que seguramente se te hará muy fácil de entender, así tienes y ahora sí puedes sumar con fracciones con distinto denominador.
Si lo ves de esta forma, también puedes decir que ya tienes 1 de kg.

Entonces si tienes para el caldo, un kilogramo y un cuarto, ¿Cuánto faltaría para los 2 kilogramos que se ocupan para la receta?
¿Cuántos cuartos se necesitan para completar otra unidad?
La cantidad de pollo que falta es kg de carne.
Para continuar con el tema resuelve el desafío 52 que se llama Sumas y Restas II. Se encuentra en la página 100 de tú libro de Desafíos Matemáticos.

https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/100
¿Estás lista o listo? ¿Lee el primer problema?

https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/100
Luisa utiliza m de listón para elaborar un moño. Si necesita 7 moños azules, 4 rojos y 5 dorados, ¿Cuántos metros de listón de cada color debe comprar?
¿Qué es lo primero que tienes que hacer?
Si es en cada moño quiere decir que con un metro de listón se pueden hacer 3 moños utiliza una tira de papel como si fuera el listón.

Si 1 metro son 3 moños, entonces si hará siete moños azules, ¿Cuántos metros de listón azul se necesitan? en 2 metros serían 6 moños.


Y más, serían los 7 moños con un total de 2 metros de listón azul.



¿Cuánto listón se requiere para los 4 moños rojos? exacto, con un metro tienes 3 moños y para el moño que falta ocupas sería 1 m. de listón rojo.
Ahora sólo te falta el listón para los moños dorados, son 5 moños dorados, ¿Cuántos metros de listón serían? Perfecto, acertaste, en un metro tienes 3 moños y los dos que faltan para 5 serían de metro quedando 1 de listón dorado.
¿Ya tienes la respuesta?
Ayudaste a Luisa a resolver el problema.
¿Qué te parece si continuas con el siguiente problema?

https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/100
En la fiesta de Saúl se sirvió helado de chocolate a todos los invitados. Después de repartir una porción a cada persona, sobraron de litro. ¿Cuánto helado tendrá que comprar la mamá de Saúl, si ahora necesita completar 1 litros en total?
¿Qué tienes que hacer para resolver este problema?
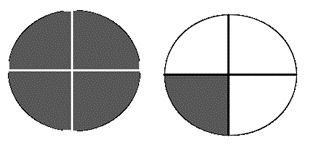
Si observas el helado que queda está representado en cuartos, entonces, la cantidad a la que tienes que llegar la vas a representar en cuartos también.
¿Cómo puedes hacerlo? utiliza fracciones equivalentes.
Haz la representación del helado que sobró, ahora representa la cantidad que necesita, averigua cuál es la diferencia entre cada representación.

Ahora los puedes contar, ¿Cuál es la diferencia? ¡Exacto! son ¾
Para continuar con el tema observa el siguiente desafío en la página 101 de tú libro de Desafíos Matemáticos. ¿Qué puedes observar ahí?
Adelante con el siguiente problema.
https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/101
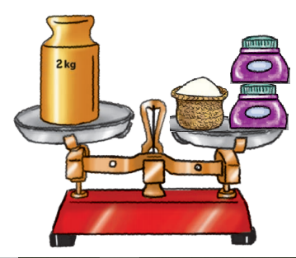
¿Cuántos frascos y cuántas cestas se deben colocar en el platillo derecho de la tercera balanza para mantenerla en equilibrio? Se deben poner tanto frascos como cestas.

Como puedes observar en la primera balanza tienes una pesa de kilogramo, ¿Cuánto pesa la cesta? Acertaste, la cesta pesa kg.
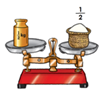
Ahora observa la siguiente balanza.

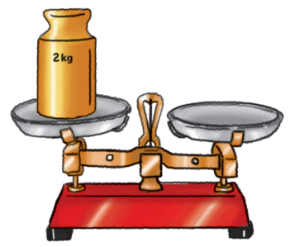
Observa que el frasco pesa lo mismo que la cesta y una pesa de kg. Si en la balanza anterior descubrimos que la cesta pesa , ¿Qué debemos hacer ahora?
Vas a sumar ¼ de la pesa más ½ de la cesta, para saber cuánto pesa el frasco.
Vas a hacer la representación para sumar, obteniendo la equivalencia de a cuartos. Con la equivalencia, puedes sumar esto sería lo que pesa el frasco.

Ahora sólo debes completar dos kilogramos, que sería lo mismo que completar dos unidades, podrías colocar 4 cestas, porque cada una pesa de dos sería 1 kilogramo y con 4 serían los 2 kilogramos.
Recuerda que el desafío dice que debes usar cestas y también frascos.
Un frasco pesa sí pones dos frascos, ¿Cuánto pesarán juntos? que es lo mismo que 1 kilogramo y dos cuartos.
Estás de acuerdo en que 1 kilogramo con dos cuartos es lo mismo que 1 kilogramo y medio. Así que, ¿Cuánto le falta a 1 kilogramo y medio para completar los dos kilogramos que indica la pesa en el otro plato?
Pues medio kilogramo. Entonces puedes poner junto con los dos frascos una cesta y ya completas los dos kilogramos.
Hoy has aprendido a utilizar fracciones equivalentes para resolver problemas de sumas y restas. ¿Te fijaste que utilizando representaciones gráficas puedes llegar fácilmente a los resultados? Inclusive utilizando cálculo mental o bien realizando directamente las sumas y restas.
¿Te gustaría seguir aprendiendo del tema? Para ello puedes trabajar resolviendo el problema número 4 que está en la página 101 de tú libro de Desafíos Matemáticos de 4to grado. Recuerda que puedes hacer las representaciones gráficas para dividir las unidades las veces que sean necesarias hasta obtener las fracciones equivalentes.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas