De brinco a brincos
De brinco a brincos
Aprendizaje esperado: usa la expresión n/m para representar el cociente de una medida entera (n) entre un número natural (m): 2 pasteles entre 3; 5 metros entre 4, etcétera.
Énfasis: anticipa números fraccionarios que expresan resultados en problemas de división.
¿Qué vamos a aprender?
Aprenderás a anticipar números fraccionarios que expresan resultados en problemas de división.
¿Qué hacemos?
Vamos a tener una interesante clase, combinaremos la actividad mental con la física, es un reto en el que daremos unos cuantos saltos y a la vez utilizaremos las matemáticas.
El ejercicio físico, es muy importante, pero también el ejercicio mental, por lo tanto, entrenar la mente y el cuerpo a la par es lo ideal para lograr el balance perfecto, a fin de potenciar al máximo todas nuestras capacidades.
Para comenzar contaremos con la ayuda de una alumna llamada Camila, que nos manda el siguiente video.
Te invito a observarlo.
- Salto de trompo de Camila.
https://www.youtube.com/watch?v=G78KcLfvMMQ
A Camila sí que le gusta saltar, ella sí que es una experta en ese salto de trompo, para activar nuestro cuerpo, vamos a realizar unos saltos de trompo para ver definitivamente y de una vez por todas, quién da los saltos más grandes.
Están listos vamos a contar, al igual que Camila, ¿Cuántos saltos pequeños das para dar una vuelta completa?
Para comprender mejor este asunto, te pido que elabores una tabla como la siguiente:

Yo las conté, Camila da 8 saltos pequeños para dar una vuelta completa.
Vamos a anotarlo, en la tabla.
Fue una vuelta y dio 8 saltos, pero ¿Cuánto vale cada salto? Lo que podemos hacer es representar los saltos con una fracción.
Queremos saber qué parte de la vuelta completa representa cada salto y con cuántos saltos damos una vuelta y además, qué relación existe entre el número de saltos y la vuelta completa.
Para representarlo, podemos decir que, si se necesitan 8 saltos para la vuelta, cada salto representa la octava parte. Lo anotaremos como fracción y será 1 el numerador, el denominador sería el número de saltos que dio que fueron 8
Porque es la cantidad de saltos que se necesita para completar toda la vuelta. En este caso, la medida del salto sería un octavo de la vuelta, por lo tanto, para representarlo podríamos hacerlo gráficamente.
Como puedes ver ahí, la vuelta completa esta representada con los 8 saltos que dio Camila y también tenemos una recta que nos ayudará a comprender esto.
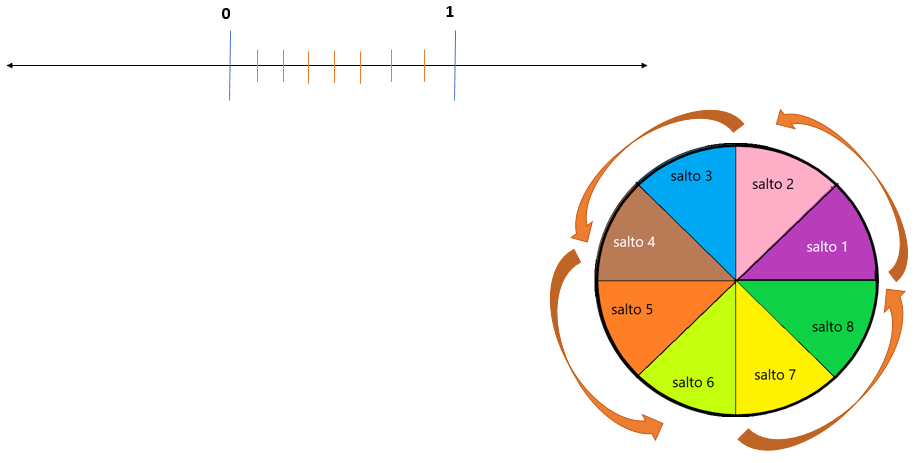
Aquí puedes observar que tenemos la recta hasta el número uno, porque sólo contemplamos una vuelta.

Las dos líneas azules representan la vuelta completa.
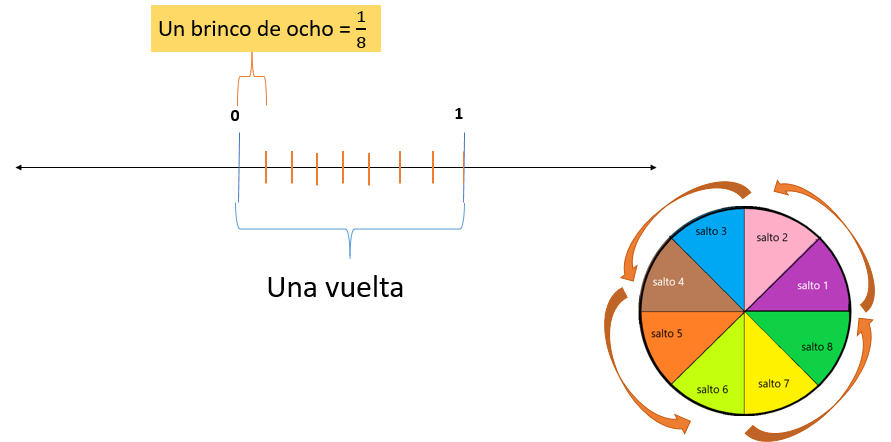
Las anaranjadas representan los saltos que da para dar la vuelta completa. Así, observamos que cada salto que dio Camila representa una octava parte de vuelta.
Entonces cada línea anaranjada representa un brinco, de 8 brincos que da en total. Podemos colocar en el numerador 1 y en el denominador 8 para representar cada brinco, aquí la fracción nos dice que se trata de un brinco de los 8 brincos que dio en total Camila y lo escribimos como un octavo.
Ahora vamos a ver cuántos saltos da Ana, en una vuelta.
Pudo dar 9 saltos en círculos. Logro dar 9 saltos para una vuelta, vamos a anotarlo en la tabla.
Con 9 saltos Ana, da la vuelta completa, es decir, avanza una unidad por cada 9 saltos. Entonces anotamos un noveno.
Puedes ver cómo hacemos ejercicio y matemáticas al mismo tiempo. Ahora le toca a Ton.
Ton da 4 saltos a la derecha, avanza una unidad con 4 saltos.
La tabla queda de la siguiente manera:
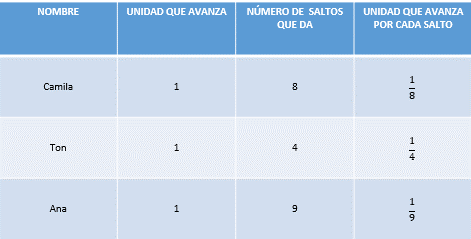
Ahora vamos a resolver el desafío número 81 “El robot”, que se encuentra en la página 160 de tu libro de Desafíos Matemáticos.
https://libros.conaliteg.gob.mx/20/P5DMA.htm#page/160
Vas a utilizar hojas y lápices para que hagas tus operaciones.
La consigna dice así:
En equipo, completen la siguiente tabla y respondan las preguntas.
Un grupo de alumnos elaboró varios robots, cada robot avanza determinada cantidad de unidades en función del número de pasos que da. Las tablas muestran esta relación.

La primera fracción es un quinto.
La segunda fracción son 2 séptimos.
Los resultados que hemos obtenido y aquellos que nos faltan, servirán para contestar las preguntas del desafío, y ambas nos dicen que comparemos cantidades.
Vamos a utilizar la forma gráfica que hace un momento vimos, para poder comparar estos dos resultados que obtuvimos.
Entonces necesitamos trazar dos rectas y comparar estos dos saltos, para saber qué robot avanza más o menos en un paso.
Analicemos las siguientes imágenes. Hay dos segmentos de recta. Uno está dividido en 5 partes iguales y el otro en 7 partes iguales.
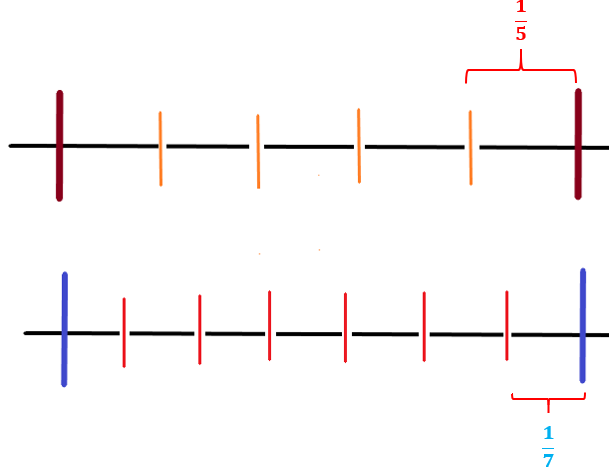
En cada uno de esos segmentos podemos indicar los pasos que dio cada robot.
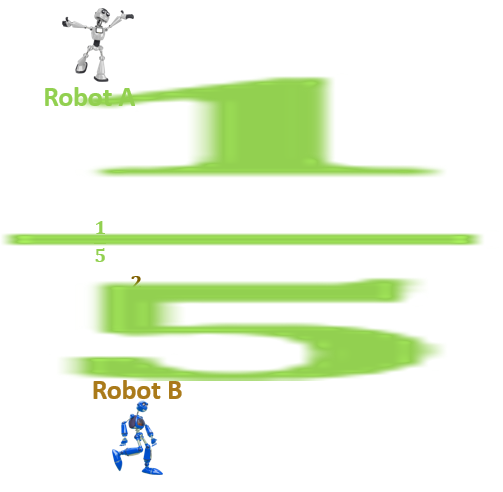
Podemos poner en la primera gráfica una letra A donde corresponda al avance del primer robot, en la segunda una B para señalar cuánto caminó el segundo robot.
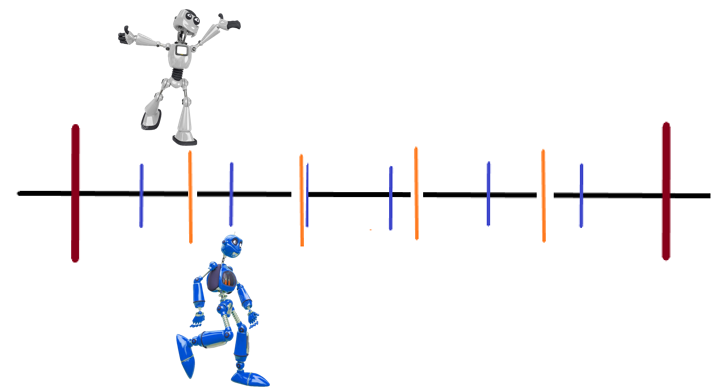
Si ponemos en un solo segmento de recta los pasos que dio cada robot, podremos saber con certeza quién avanzó más.
Con la representación gráfica queda clarísima la comparación de las dos fracciones.
Lo único que me preocupa es que habrá ocasiones en que será muy tardado hacer las gráficas, por ejemplo, aquí nos piden comparar los pasos de 10 robots, imagínense cuánto nos tardaremos en hacer diez gráficas y luego en juntarlas todas, además de tardado, en la gráfica estarían muy encimados los robots y ya no se apreciaría mucho.
Así que, no nos queda más que comparar las fracciones, como ya lo hemos hecho.
Vamos a comparar los pasos de dos robots.
Continuemos con el robot C avanzó cuatro unidades y para eso necesitó 10 pasos. Así que esto se expresa mediante una fracción como cuatro décimos, esa fracción la podemos reducir y quedaría de la siguiente forma.

Vamos a saber cuánto avanzó el robot E así que veo que en la tabla se registró un avance de 10 unidades, caminó 10 unidades y para eso necesitó 30 pasos, entonces, al expresar su avance en fracciones tenemos, 10 entre 30 pero también esta fracción se puede reducir, por lo que nos queda.
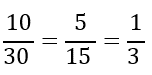
Ahora lo único que nos falta por determinar es qué fracción es mayor, o menor.
Podríamos hacer la división de ambas cantidades, es una estrategia muy buena por ser rápida y precisa, así que ya te tengo el resultado de las divisiones.

Ya sabemos cuál de los dos robots avanza más. El robot C le ganó al robot E. Como puedes ver el robot E, a pesar que de que dio mas pasos, no fue el ganador.
Estas dos estrategias que vimos aquí no son las únicas con las que podemos llegar al resultado, así que te invito a que ensayes y compruebes cualquier otro camino que puedas hallar para resolver este desafío.
El reto de hoy:
Resuelve la cantidad de unidades en función del número de pasos que da cada robot de las letras D, F, G, H, I y J de la tabla y contesta las preguntas se los incisos a) y b) del desafío número 81 “El robot”, que se encuentra en la página 160 de tu libro de Desafíos Matemáticos.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas
