¿Cuántos enteros sobran?

¿Cuántos enteros sobran?

Aprendizaje esperado: análisis de las relaciones entre los términos de la división, en particular, la relación r = D − (d ✕ c), a través de la obtención del residuo en una división hecha en la calculadora.

Énfasis: aplica las relaciones entre los términos de la división al proponer divisiones que cumplen con la condición de un residuo predeterminado.

¿Qué vamos a aprender?

Aplicarás las relaciones entre los términos de la división al proponer divisiones que cumplen con la condición de un residuo predeterminado.

¿Qué hacemos?

Estuve leyendo un artículo muy interesante y pensé, ¿Quién será más rápido para hacer cálculos? Una persona o una máquina.

Tú, ¿Quién crees que ganaría entre una calculadora y el cerebro humano? ¿Te lo has preguntado?

La calculadora lo hace en un segundo y todo es correcto, pero te diré tres cosas a favor del cerebro humano que he pensado:

1. El cerebro humano hace muchas más cosas que operaciones.
2. El cerebro humano encuentra el camino para solucionar los problemas y sabe cuáles son las operaciones que se deben hacer para llegar a la solución de un problema matemático.
3. El cerebro humano inventó la calculadora.

Para la sesión de hoy vas a necesitar una calculadora, el reto consiste en lo siguiente, pon mucha atención.

Vas a calcular el residuo de una división, te voy a indicar qué vas a dividir y tú deberás encontrar el residuo. ¿Listos?

¿El reto sería así? por ejemplo, dividir 110 entre 25, haciendo la división en la calculadora y después comentaremos cuál es el residuo de la división.

La primera operación es 245 entre 25.

Recuerda que en la división son importantes el cociente y el residuo porque los dos forman parte del resultado.

Ahora verifiquemos el resultado.

Primero se divide 245 entre 25 y el resultado en la calculadora es 9.8, tomando solo el entero; después, se multiplica 9 por 25, lo que resulta 225 y luego se resta al 245 y sobran 20 es decir, es el residuo en enteros.

¿Sabes por qué en la calculadora te salió un resultado con decimales?

Reflexiona, ¿Cuál es el residuo en tu división?

R = Es 20

Y ese residuo, ¿Es mayor o menor que el divisor?

R = Es menor.

¿Piensas que pueda haber alguna relación entre en divisor, el residuo y por qué el cociente salió con decimales en la calculadora?

R = Como 245 se reparte entre 25, alcanza para 9, pero los 20 que sobran ya no alcanzan, entonces hay que partirlos en pedacitos, por eso salen decimales.

Observaste, ¿Cómo el cerebro es mejor que la calculadora? Ahora veamos esta otra división.

El resultado de la división 444 entre 24 en la calculadora da 18.5 luego se multiplica 18 por 24, son 432 y se resta a 444 y el residuo es 12.

Vamos a analizar, ¿Por qué salió 18.5?

Salieron decimales en la calculadora, porque al repartir el residuo 12 entre 24, ya no alcanza y sólo se puede si tocan fracciones.

Vamos a la siguiente división. 550 entre 16.

Ahora sobran 6. Cuando divides en la calculadora 550 entre 16, salen 34.375, de este resultado sólo toma la parte entera que es 34 y lo multiplicas por 16, esto es igual a 544, ya sólo debes restar a 550 y son los 6 que sobran.

El residuo es 6 y ya no alcanza para repartirlo entre 16, y entonces cuando usas la calculadora lo que hace es poner el punto decimal para indicar que salen pedacitos o fracciones.

Pasemos a la siguiente división 480 entre 50.

Aquí sobran 30. Si divides 480 entre 50 sale 9.6 en la calculadora, se multiplica sólo el 9 por 50 y son 450 lo restas a 480 y el residuo es 30. Y como ya te imaginas salió 9.6 porque ya se están obteniendo pedacitos de lo que se reparte, eso quiere decir que, si divides 30 entre 50 ya no alcanza para que sean enteros.

Vamos con la siguiente división 340 entre 25.

Aquí sobran 15.

Verifica si está bien tu resultado con la calculadora.

Al teclear 340 entre 25 en la calculadora, el resultado es 13.6 como ya sabes cómo encontrar el residuo, da 15 y como 15 es menor que 25 por eso te saldrán decimales en la calculadora.

Recuerda que la calculadora siempre da decimales cuando el resultado no son enteros exactos.

Siguiente division.

El residuo es 15.

Primero deberás dividir 365 entre 25 en la calculadora sale 14.6 luego debes multiplicar 14 por 25 y sale 350 lo restas a 365 y también son 15. El cociente es 14.6 porque la calculadora repartió el residuo entre 25 y como ya no alcanzaba para otro entero, entonces lo fraccionó.

Espero hayas entendido la relación entre todos los elementos de la división.

¿Te diste cuenta de que hubo divisiones que tuvieron el mismo residuo?

La siguiente tarea a realizar es buscar una división que también te dé otra vez como residuo 15.

Te sugiero analizar las divisiones donde el residuo fue 15. Revisa las operaciones que hiciste, ahí puedes encontrar una pista.

Creo que no te será difícil, pues el divisor no cambia y si al dividendo le aumentas 25, tendrás la respuesta, otra manera para obtener como residuo 15, es dividir 390 entre 25.

Compruébalo.

Teclea 390 entre 25 en la calculadora, da como resultado 15.6 multiplica 15 por 25 y da 375 y eso se resta a 390 y da 15 como residuo.

Si divides 365 entre 25 y le sumas otros 25 al dividendo, seguramente aumentará el cociente, pero el residuo se quedará igual. Compruébalo.

¿Habrá más divisiones donde el residuo sea 15? Analiza y anótalas en tu cuaderno.

Ahora vamos a resolver el Desafío número 42 “Con lo que te queda”, que se encuentra en la página 85 de tu libro de Desafíos Matemáticos.

Aquí sólo utilizaras la calculadora para comprobar los resultados.

Antes de contestar, debes considerar que el residuo siempre debe ser menor que el divisor, pues si es igual o mayor podemos seguir haciendo repartos enteros.

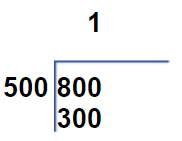
800 entre 500. Toca a 1 y sobran 300.

Ya tienes la primera división, faltan dos más.

Si retomas el procedimiento de los retos anteriores y le sumas al 800 los 500 serían 1300 entre 500 toca 2 son 1000 y sobran 300.

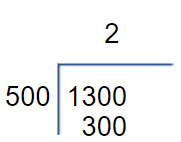
Para la siguiente división puedes sumar otros 500 a 1300 entonces tendrás 1800 entre 500, toca a 3 y sobran 300.

Bien ya están las tres divisiones, ahora contesta las preguntas.

¿Se pueden escribir más divisiones con estas condiciones? y ¿Cuáles son?

R = Sí se puede, siempre y cuando el residuo sea más chico que el divisor.

Siguiente pregunta, ¿Cuántas divisiones se pueden escribir con el residuo de 300?

R = Muchas, si aumentas 500 al número que se divide, el residuo siempre será 300 sólo cambiará el cociente.

Las posibilidades son muchas, siempre y cuando tengas muy en cuenta que el divisor siempre tiene que ser mayor que el residuo. De esta manera has resuelto el desafío de tu libro.

Recuerda que existen varias formas en las que puedes razonar para saber cómo resolver un problema, el día de hoy con las actividades del reto y la solución al desafío, aplicaste las relaciones que hay entre los términos de la división, para buscar divisiones que den un residuo predeterminado.

Es importante que no dejes de aplicar los aprendizajes adquiridos en cualquier parte de tus actividades del día, en las que se puedas resolver problemas.

El razonamiento es el camino para seguir para resolver cada problema y el uso que le diste a la calculadora, sólo fue para comprobar algunos de los ejercicios. La calculadora es una herramienta muy útil, pero que no va a pensar por ti.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/