¿Cuál es la mejor representante?
¿Cuál es la mejor representante?
Aprendizaje esperado: usa la media (promedio), la mediana y la moda en la resolución de problemas.
Énfasis: identifica la mediana de un conjunto de datos y advierte su representatividad en comparación con la media aritmética.
¿Qué vamos a aprender?
En esta sesión aprenderás a resolver problemas al usar la media, es decir el promedio, e identificar la mediana de un conjunto de datos y su representatividad, así como la moda.
Los materiales que vas a necesitar son, tu libro Desafíos sexto grado, tu cuaderno u hoja para tomar notas, lápiz, goma, sacapuntas y mucha disposición.

¿Qué hacemos?
En esta sesión iniciarás con el tratamiento y la presentación de un conjunto de datos estadísticos, vas a saber cómo elegir ciertas medidas numéricas que los representan y los resumen. Presta atención y toma nota de todo aquello que te ayude a comprender este contenido.
Conoce la experiencia que tuvieron dos equipos de estudiantes al realizar un juego con dados y describir el promedio de puntos que obtuvieron.
Cada equipo registró los resultados de lanzar todos, un dado al mismo tiempo y luego buscaron el valor numérico que mejor representaba cada distribución de datos.
¿Cómo? ¿Cada distribución de datos? ¿Qué es eso?
La distribución de datos es la lista de valores de un conjunto de datos que pueden corresponder a una gran variedad de situaciones, por ejemplo, los resultados de un juego, de un experimento, al observar un fenómeno o al aplicar un estudio o una encuesta.

¿Qué es eso de representante?
Actividad 1
Busca en el diccionario la palabra representante.

Entonces un representante es la persona, el valor, la figura o el objeto que se usa en lugar de todo un grupo de personas u objetos.
Así es, y este concepto también se aplica a las matemáticas, particularmente, en la estadística, por ejemplo, al referirte al color más vendido de un determinado artículo o producto, estás usando el valor del dato que registró la mayor frecuencia.
¿Recuerdas cómo se le llama a esa medida que corresponde al dato estadístico que más veces se observa o registra?
Se llama frecuencia. Los artículos que más se venden por la razón que sea, tienen una mayor frecuencia que otros.
Entonces a eso se refieren cuando dicen que algo está de moda, es porque la mayoría lo tiene, porque se repite muchas veces.
Volviendo al caso de los estudiantes, los alumnos registraron los datos que obtuvieron al lanzar un dado cada uno y al mismo tiempo. Inició el equipo de los genios matemáticos.
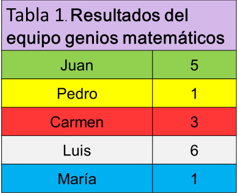
Esos son los números que les salieron y los registraron en una tabla como la siguiente.
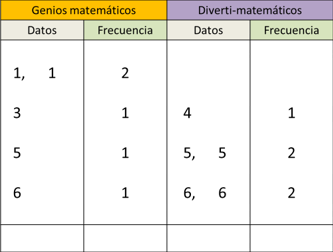
Ahora, vamos con el equipo de los “divertí-matemáticos” que muestra los resultados de su tirada.

¿Cuál número se repite más en los resultados del equipo divertí-matemáticos?
Observa los resultados de ambos equipos.

¿Cuál es el resultado que más veces se registró?
En el primer equipo el número 1 cayó dos veces y, en el segundo equipo, el 5 y el 6 ambos números se registraron dos veces.
En ese caso coincide su frecuencia y, además, es la mayor frecuencia que se registró.
En la tirada del primer equipo, el 1 se registró dos veces, fue el que más apareció, en la otra, el 5 y 6 son los números que tienen mayor frecuencia, y también aparecieron en 2 ocasiones cada uno.
En ese caso, ¿Cuál valor se considera como el más frecuente, el 5 o el 6? ¿Cuál de los dos sería la moda?
Ambos valores son la moda, esa es una de las características de esa medida que debes tener en cuenta, ya que puede ocurrir que se presente uno, dos o más datos que tengan la misma frecuencia y que ésta sea la mayor. Observa entonces que el valor de la moda conviene cuando se necesita conocer cuál es el dato que se registra más veces en un conjunto de datos, por ejemplo, en cuestiones de ganancias, competencias, compras, preferencias o disponibilidad.
Señala tanto al par de unos como a los pares de 5 y 6
Para el juego con dados conviene saber si hay un número que sale más veces que otro para elegirlo y ganar.
Ahora, considera que los equipos están buscando otros valores que también representen al conjunto de resultados que obtuvieron. Recuerda que la media aritmética es un promedio que se utiliza para representar un conjunto de datos. Por ejemplo, tu calificación anual de sexto grado es el promedio de las calificaciones de las asignaturas en cada trimestre.
Hay muchos ejemplos de donde sacar promedios.
Calcula el valor de la media aritmética o promedio de estos dos conjuntos de datos.
Después de sumar los valores de todos los datos, se divide entre el número total de datos. En este caso, ¿Cuántos datos registró cada equipo en total? Es decir, al hacer la tirada, ¿Cuántos dados lanzaron en cada equipo?
Cinco, porque eran cinco jugadores que tiraron su dado al mismo tiempo.
Entonces son 5 datos y hay que sumar sus valores para poder calcular el valor de la media aritmética o promedio, la de los resultados del equipo 1 y la de los del equipo 2.
Puedes hacer uso una calculadora para apoyar los cálculos. Hay que obtener la media aritmética o promedio del equipo 1 y equipo 2.
Para obtenerla hay que sumar: 1 más 1 más 3 más 4 más 5 y más 6 son 16, ahora el total, se divide entre 5. El valor de la media aritmética del equipo 1 da: tres enteros dos décimos (3.2).
El del equipo 2, da como resultado: 5.2
¿Por qué da números decimales? ¿Hay algo mal en estos valores de la media aritmética? porque son números decimales y los números de las caras de los dados que lanzaron, ninguno tiene ese tipo de valor.
Esto se debe a que el valor de la media aritmética es el resultado de una división, es decir, es un cociente. Se obtiene de la suma total de los valores de los datos entre el número total de datos. Como saben en algunas divisiones el resultado es exacto, esto ocurre cuando el residuo es cero. Y en el caso de la media aritmética pueden suceder tres casos.
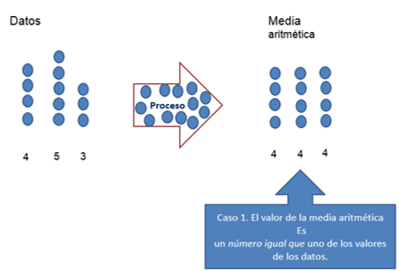
El primero es que su valor sea igual al de uno de los valores de los datos, por ejemplo, aquí se suma 4 + 5 + 3 es igual a 12 y se divide entre 3 entonces el valor de la media aritmética es 4 este valor es el representante de los tres valores iniciales.
En este conjunto de tres datos, al 4, al 5 y al 3 los representa el 4, porque ése fue su promedio o media aritmética.
Ese es un primer caso, cuando el valor de la media aritmética coincide con uno de los valores de los datos.
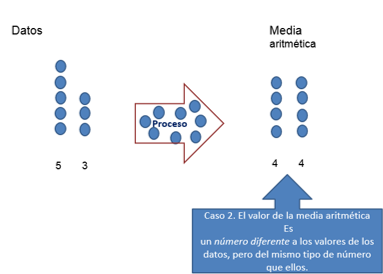
Pero puede ocurrir que no sea así. Por ejemplo, se puede obtener un valor que sea diferente a los datos, pero que es del mismo tipo de número, como ocurre en este ejemplo, observa, ¿Cuál es la media aritmética de 5 y 3?
Es 4 porque al sumarlos es 8 y 8 entre 2 es 4
Eso significa que la división es exacta, pero 4 no es un valor de alguno que exista en los datos de este conjunto, entonces el 2 es representante de 5 y 3, y es un número del mismo tipo.

También puede suceder que obtengas un valor de la media aritmética que es distinto a los valores de los datos y también es de una forma distinta que los datos.
Ejemplo, si se necesita calcular la media aritmética de 6 y 3, la suma es 9, y al dividir entre dos el resultado es 4.5
Esto ocurre porque la división entre la suma total de los datos y el número de datos no fue exacta, hay residuo e implica que el cociente es una expresión decimal.
También en este caso el 4.5 es representante del conjunto formado por el 6 y el 3
Pero es necesario conocer cuándo esta medida es útil para representar un conjunto de datos, pues, aunque es muy común su uso, no siempre es la mejor representante de los datos que se están analizando.
Y en esa situación, ¿Qué se puede hacer?
Se recomienda obtener otra medida que también puede representar al conjunto de datos.
¿Y cuál es esa otra medida?
Es la mediana, así se le dice porque corresponde a la posición central de los datos.
Observa por qué.
Debes considerar que la posición central de un conjunto de datos corresponde a la posición en la que se divide al conjunto de datos en dos partes con igual número de datos. Para lo cual requieres que los valores de los datos estén ordenados, ya sea de mayor a menor o de menor a mayor. ¿Crees que ya se cuenta con eso en los dos ejemplos o hay que ordenarlos?
Cuando se elaboraron las tablas con los resultados de los dos equipos, se ordenaron.
Pero, cuando tengas un conjunto de datos, si no están ordenados los debes ordenar, ya sea de mayor a menor o de menor a mayor, como se muestra en la tabla siguiente:

Aquí los tienes de nuevo, y puedes verlos en cualquiera de los dos sentidos.
Esto es útil para encontrar cuál es el dato que está en el centro de todos ellos. Entonces, para el equipo “divertí matemáticos”, primero dos veces el 6, luego dos veces el 5 y, por último, el 4.
6 6 5 5 4
Ahora para ubicar cuál es el dato que queda en medio, debes ver cuál es la posición central. ¿Ya lo identificaste?
Sí, el 5
6 6 5 5 4
Porque antes que él hay dos valores y también después de él hay dos valores.
Ese es el valor de la mediana, de los resultados del equipo Divertí matemáticas.
Y el valor de la mediana, ¿Siempre es la posición que queda en el centro del conjunto cuando los datos están ordenados?
Sí, ese valor es muy útil porque puede ser el mejor representante cuando hay valores muy pequeños o grandes en los extremos del conjunto ordenado de datos.
¿Cuál es el valor de la mediana en el conjunto de resultados del equipo genios matemáticos?
Se observa que también es un conjunto de 5 datos, entonces la posición central es la tercera, el valor ubicado en esa posición es el 3.
Ahora, compara los valores de las tres medidas que has obtenido para cada conjunto de datos y determina cuál representa mejor a cada uno.
Entonces se sabe que para el primer equipo la moda es 1, la mediana es 3 y la media aritmética es 3.2 en el caso, del segundo equipo, hay dos modas, 5 y 6 la mediana es 5 y la media aritmética es 5.2
| Genios-matemáticos | Diverti-matemáticos | ||
| Datos | frecuencia | Datos | frecuencia |
| 1,1 3 5 6 |
2 1 1 1 |
4 5,5 6,6 |
1 2 2 |
| 5 | 5 | ||
| Media aritmética | 3.2 | 5.2 | |
| Moda | 1 | 5 y 6 | |
| Mediana | 3 | 5 | |
Como representante de cada conjunto de resultados podría utilizarse a la mediana.
Porque en el contexto del juego con dados, la media aritmética no es muy conveniente porque son números decimales. Sin embargo, en ambos casos, los valores de la media aritmética, 3.2 y 5.2, están cercanos a los valores de la mediana, 3 y Con respecto a la moda, su valor, en el primer conjunto de resultados es 1, que es un valor extremo del conjunto de valores, y la moda del otro conjunto, tiene dos valores, no es único.
Con lo que has trabajado en esta clase, ya tienes más herramientas para resolver el desafío 52 que está en la página 104 de su libro de texto.
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/104

Da lectura a la consigna.

Actividad 1
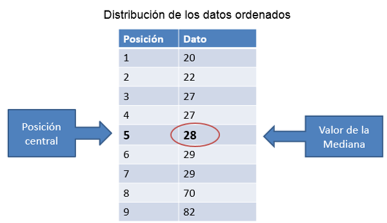
En una reunión hay 9 personas, sus edades en años son las siguientes.
La imagen presenta a las personas que conforman la reunión y cada una muestra su edad en años, anotada en su ropa.

27, 22, 29, 27, 82, 20, 28, 29,70
- ¿Cuál es la media aritmética (promedio) de las edades?
b) ¿Qué procedimiento usaste para encontrarla?
Resuelve también las actividades 2 y 3.
Para la segunda actividad debes ordenar los nueve datos que te dan sin dejar de escribir ninguno.

Recuerda indicar cuáles son las posiciones que tienen los valores de los datos.
Durante esta semana vas a seguir estudiando las características y significados de estas medidas.
Seguramente ya has recordado lo que aprendiste sobre el tema de media aritmética, mediana y moda.
Al resolver este desafío has comprendido aún más el significado que tienen estas medidas.
Ten presente que eres inteligente, no olvides utilizar con responsabilidad tus dispositivos electrónicos, organiza tu tiempo, recuerda que las matemáticas están en todos lados, son interesantes y pueden ser divertidas.
El reto de hoy:
Comparte lo que aprendiste respecto de la mediana aritmética, la moda y la mediana con tu familia, explícale los ejemplos que trabajaste y como lo hiciste, seguramente le parecerá muy interesante.
Si te es posible, consulta otros libros y materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa*.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/P6DMA.htm