Contorno y superficie
Contorno y superficie
Aprendizaje esperado: calcula aproximadamente el perímetro y el área de figuras poligonales mediante diversos procedimientos, como reticulados, yuxtaponiendo los lados sobre una recta numérica, etcétera.
Énfasis: distingue el perímetro y el área de figuras poligonales, mediante el trazo de polígonos cuyos perímetros y áreas estén determinados.
¿Qué vamos a aprender?
Aprenderás a calcular el perímetro y el área de figuras poligonales.
¿Qué hacemos?
¿Recuerdas cuál es el área y cuál es el perímetro de una figura? A la medida de la superficie de una figura se le llama área y al contorno se le llama perímetro.

Para iniciar la sesión de hoy vas a armar figuras diferentes, pero que todas tengan exactamente seis unidades cuadradas de área.

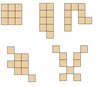
Observa las siguientes figuras.


Aquí otra idea.

Esta figura parece una U, pero parece que los cuadros están separados. Observa que están unidos por sus vértices, por eso se puede decir que es una sola figura. Todas estas figuras tienen la misma área. Cuenta las unidades cuadradas que forman cada figura, todas tienen un área de seis cuadrados.
No importa si las figuras se ven distintas o unas más grandes que otras, lo importante es la superficie. Ahora tienes un desafío, ¿Cuál de las cuatro figuras tiene el mayor perímetro? La figura verde tiene 6 unidades cuadradas de área y 10 unidades de perímetro.

La figura roja tiene 12 entonces tiene 6 unidades cuadradas de área y 12 unidades de perímetro.
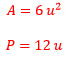
La figura amarilla tiene 14 tiene 6 unidades cuadradas y 14 unidades de perímetro.
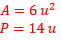
La última figura tiene 18 esta tiene un perímetro mayor que todas las demás.
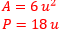
¿Qué puedes concluir de esto que acabas de hacer? Se puede decir que todas las figuras tienen la misma área, pero perímetro diferente. También que varias figuras con diferente forma pueden tener la misma área, pero el perímetro cambia.

Fuente: https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/149
Ahora prepárate con tu libro de Desafíos Matemáticos en la página 149. El desafío dice así: Dibujen en la cuadrícula:
- Una figura que tenga un área de 9 unidades cuadradas.
- Una figura que tenga 16 unidades de perímetro.
- Una figura que tenga un área de 4 y unidades cuadradas.
Y ahí te presenta la unidad de medida qué sería uno de los cuadrados. Para la figura de 9 unidades cuadradas puedes hacerla así.

Aquí tienes una idea más para una figura de 9 unidades cuadradas.
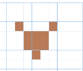
Realiza tu propia figura de 9 unidades cuadradas en tu libro de Desafíos Matemáticos. Puedes compartir con tu familia para ver que otras ideas tienen.
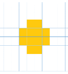
Observa cuánto mide el perímetro de estas dos figuras. Las dos figuras tienen 9 unidades cuadradas de área, pero determina cuál tiene mayor perímetro. Cómo podrás darte cuenta las dos tienen 20 unidades de perímetro, en este caso coincidió que las dos figuras tuvieran la misma área y el mismo perímetro.
En casa y en compañía de tu familia podrías hacer figuras y poner como condición que además de tener la misma área, tuvieran el mismo perímetro, o ver quién hace la figura con la misma área y el mayor o el menor perímetro, seguramente se divertirán.
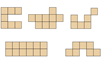
A continuación, observarás otras ideas de figuras con 9 unidades cuadradas de superficie.
Como puedes ver la primera es un cuadrado porque tiene tres por tres unidades. Observa la última parece un insecto con patas largas. Hay muchas formas de hacer figuras con 9 unidades cuadradas, esos solo fueron unos ejemplos.
Ahora observa la siguiente indicación de tu libro, dice que debes dibujar una figura con 16 unidades de perímetro.
Inténtalo, seguramente pensaste en la siguiente figura.

Llegaste sólo a 12 unidades de perímetro, te faltan algunas. Si agregas dos arriba y dos abajo te quedaría de la siguiente forma.
En el primer intento la figura tenía sólo 12 unidades, y se le agregaron dos cuadrados encima para obtener 4 unidades más.
Otra figura que podrías hacer con 16 unidades de perímetro es la siguiente.

Observa otras formas en las que se pueden hacer figuras de 16 unidades de perímetro.
Estas formas son diferentes y todas miden 16 unidades de perímetro.
En el siguiente tienes que hacer una figura con 4 ½ unidades cuadradas. ¿Cómo lo harías?

Puedes contar cuatro y agregar una mitad para que sean 4 ½. El uso de los triángulos es una gran idea.

Ahora continúa con la página 150 de tu libro de Desafíos Matemáticos de cuarto grado.

Fuente: https://libros.conaliteg.gob.mx/20/P4DMA.htm?#page/150
Para el trazo del inciso C, cuatro alumnos dibujaron las siguientes figuras; verifiquen si cumplen o no con la condición y escriban por qué. Revisa la primera figura.

Aquí tienes 2 unidades cuadradas ya, si juntas los dos triángulos de la izquierda llevas 3, y si juntas los dos triángulos de la derecha son 4. El triángulo que queda solo es ½, entonces es correcto, son 4 ½ unidades cuadradas.
Observa la siguiente figura.

Son 3 unidades cuadradas que ya están ahí, solo que están de lado, luego tienes tres triángulos, si unes dos, llegas a 4 unidades cuadradas. Te queda un triángulo que sería ½, entonces sí, esta figura también está correcta, son 4 ½ unidades cuadradas.
Ahora observa esta imagen.
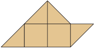
Si observas detenidamente tienes cuatro triángulos, cada par se puede unir para formar 1 unidad cuadrada, pero faltaría un triángulo más para representar ½. Por lo tanto, esta figura tiene solo cuatro unidades cuadradas.
Ahora observa la última figura.

En esta figura hay 2 unidades cuadradas, dos pares de triángulos que formarían otras 2 unidades cuadradas, con un triángulo más que representaría ½ esta es correcta son 4 ½ unidades cuadradas.
Construye las demás figuras que piden con las características que se señalan en el libro. Si te es posible compáralas con tus compañeros y muéstralas a tu maestra o maestro.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas