¿Cómo divido?
¿Cómo divido?
Aprendizaje esperado: resuelve problemas que impliquen una división de número fraccionario o decimal entre un número natural.
Énfasis: encuentra un procedimiento para dividir una fracción entre un número natural, cuando el numerador de la fracción es múltiplo del natural.
¿Qué vamos a aprender?
Resolverás problemas que impliquen una división de número fraccionario o decimal entre un número natural, así también deberás encontrar un procedimiento para dividir una fracción entre un número natural, cuando el numerador de la fracción es múltiplo del natural.
¿Qué hacemos?
Trabajarás con situaciones que implican operar con fracciones. Estos temas que estudias aquí te pueden ayudan a resolver situaciones que se te presenten en la vida real. Para comenzar revisa el problema que envía Horacio, un niño de la escuela Revolución Mexicana. Lee el mensaje de Horacio.

El problema 1 dice lo siguiente:

¿Cuál crees que sea la respuesta correcta? Te ayudarán unos dibujos para resolver esto, muchas veces un dibujo puede ayudarte a comprender mejor un problema. Puedes imaginar que este rectángulo es el terreno destinado para sembrar y como a la escuela le donaron 6 octavas partes, entonces lo divides en 8 partes iguales y de ésas tomas las 6 que dieron a la escuela.
Concéntrate en esas 6 partes que son las que se van a repartir entre los grupos de la escuela. ¿Recuerdas cuántos grupos son? Horacio dice que en uno estudian primero y segundo, en otro tercero y cuarto y en el otro, quinto y sexto, entonces son tres grupos.
¿Y cómo repartirías esos 6 octavos entre los tres grupos para que a todos les toque un terreno igual? Puedes anotar así en cada fracción.
| Primero y Segundo | Tercero y Cuarto | Quinto y Sexto | |
| Primero y Segundo | Tercero y Cuarto | Quinto y Sexto |
Entonces, ¿Cuál sería tu respuesta? Dos. No es claro si son sextos o son octavos, porque estás repartiendo 6 partes. Analízalo, ¿En cuántas partes está dividido el terreno? En octavos, pero estás repartiendo 6. Sí, pero esas 6 partes que estás repartiendo, ¿Qué fracción del entero representan? Pues cada parte representa un octavo. Exacto, lo que estás repartiendo son octavos no sextos.
Recuerda que cuando repartes fracciones, no cambia el tamaño de la fracción. Entonces la respuesta es que a cada grupo le tocan 2 octavos. Esa es la respuesta correcta, dos octavos. ¿Y qué sucede si haces esto?
| Primero y Segundo | Tercero y Cuarto | Quinto y Sexto | |
| Primero y Segundo | Tercero y Cuarto | Quinto y Sexto |
Pues divides el terreno en 4 partes iguales. Y de esas 4 partes iguales, ¿Cuántas le corresponden a cada grupo?

Observas cómo también puedes decir que a cada grupo le toca una cuarta parte del terreno que les donaron, por lo tanto, hay dos respuestas correctas del problema que envía Horacio.
¿Recuerdas cómo se les llama a dos fracciones que se escriben de forma diferente, pero que representan la misma cantidad? Se les llama fracciones equivalentes.
Ahora analiza el segundo problema que envía Horacio.

Observa cómo puedes resolver este problema. ¿Tienes ya tu respuesta o alguna idea de cómo resolverlo? No te dice cuántos tambos compraron, ¿entonces cómo puedes hacerlo? Como desconoces la cantidad de tambos que compraron, piensa en ellos como un todo, es decir como un entero.
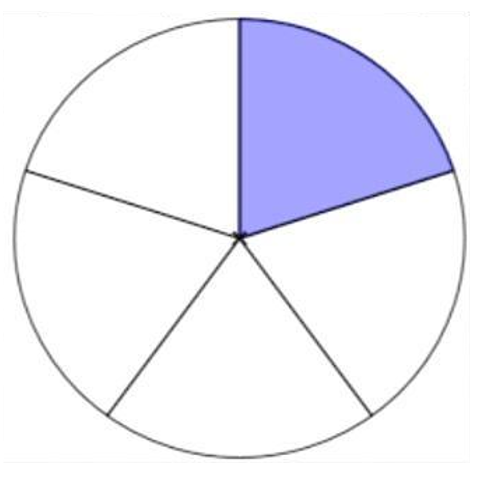
Y de este entero, te dicen que destinaron una quinta parte para el servicio de la escuela. Así que esa parte no la consideras, porque ya está destinada, entonces dejaron 4 quintos para las necesidades de limpieza y para el riego.
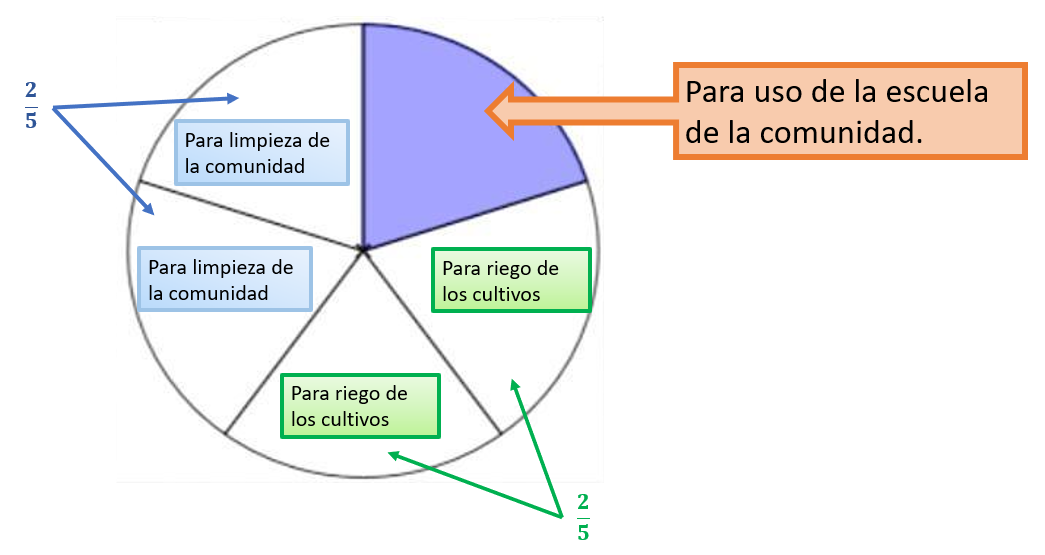
Y esos 4 quintos los divides en partes iguales para dos aspectos que les interesan, la limpieza de la comunidad y el riego de sus cultivos, es decir, dividieron en partes iguales lo que quedó, así que la respuesta, ¿Es un medio? Reflexiona, esa no es esa la respuesta. Te está faltando considerar algo, no estás considerando que lo que están dividiendo entre 2 son 4 quintos no un entero.

Es cierto, sucedió lo mismo que con el otro problema, entonces de los cuatro quintos, dos quintos son para limpieza de la comunidad y dos quintos para el riego. Recuerda que lo que estás dividiendo son fracciones en las que ya estaba divido el entero, es decir, tu referente son las fracciones, ya no es el entero.
Tal vez hiciste dibujos para llegar al resultado, pero no siempre puedes estar haciendo dibujos. ¿Hay otra forma de representar estas situaciones que no sea con dibujos? ¿Algo así como una operación? La respuesta es si. Regresa al primer problema, ahí se decía que había 6 octavos de un terreno que se debía repartir entre 3 grupos, eso puedes escribilo así:
Y el resultado al que llegaste, ¿lo recuerdas? Fue 2 octavos y luego también observaste que era igual que 1 cuarto.
Identificas que al escribir el resultado en la operación se descubre cómo se resuelve esa operación. Cuando divides la fracción entre un número entero, sólo se divide el numerador y el denominador queda igual y un cuarto sale de que simplificas la fracción. ¿Y sucede lo mismo en el segundo problema?
Recuerda que habías dividido en quintos la cantidad de tambos que compraron para juntar agua de lluvia.
De ellos ya habían donado un quinto para la escuela, así que ese ahorita ya no lo cuenta, entonces se quedaron con 4 quintos de la cantidad de tambos, y luego esos 4 quintos lo dividiste en dos, uno para riego y otro para limpieza.
Observa que también se cumple que, al dividir 4 quintos entre dos, el resultado sale de dividir entre 2 el numerador y el denominador queda igual.

Llegaste a una buena conclusión. Cuando hay una fracción que se divide entre un número entero y el numerador de la fracción es múltiplo del número entero, se divide el numerador y el denominador queda igual.
Ahora resuelve el último problema que envió Horacio.

Es muy claro lo que tienes que hacer para resolver este problema, se trata de hacer una división, porque la repartición será en partes iguales. Cuando tienes que hacer un reparto en partes iguales, lo debes representar con una división. ¿Cómo quedaría esa división? Pues sería 10.5 entre 7 ¿Se te ocurre otra forma de hacer esa repartición si no sabes hacer divisiones donde hay punto decimal? Nuevamente podrías apoyarte con un dibujo. Si separas lo que se obtuvo de calabaza en medios kilogramos puedes hacerlo. ¿Por qué en medios kilogramos? Porque son 10 y medio, entonces todo lo puedes poner en medios kilogramos y ¿Cuántos medios vas a tener? después, ¿Qué más haces con eso?

Ya sabes lo que ayuda tener un dibujo de la situación. En la imagen anterior están los 7 alumnos y alumnas que se van a repartir la cosecha de calabazas. Así que puedes comenzar a repartir bolsas de medio kilogramo y, como se ve en el dibujo, a cada uno le tocan 3 bolsas, es decir un kilogramo y medio de calabaza.
Te ayudó apoyarte en un dibujo, que bueno que las cantidades no eran más grandes, porque si no con tantas flechas, yo creo que te habrías confundido, por eso debes saber cómo se hacen esas divisiones.
La situación que plantea el problema se representa con una división como ésta:
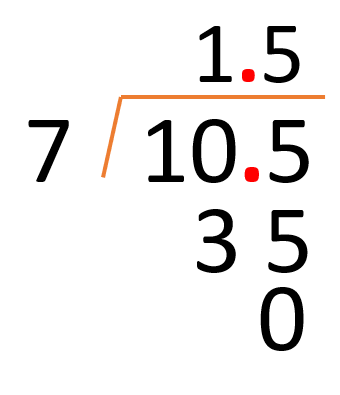
Tienes que se van a repartir 10 kilogramos y medio entre 7 alumnos en partes iguales. Cuando el dividendo es el único que tiene punto decimal, haces la división como has aprendido y subes el punto decimal al cociente en el mismo lugar donde se encuentra en el dividendo.
Entonces 10 entre 7 toca a 1 por 7 son 7 para 10 son 3 aquí observa que ya repartiste la parte entera. Ahora ve con la parte decimal, así que es aquí donde el punto decimal se coloca en el cociente. Bajas el 5 y tienes 35 entre 7 son 5 por 7, 35 para 35, 0 aquí terminó la división y como puedes ver el resultado fue 1.5 y el residuo cero.
Esto es, a cada alumno le corresponden 1.5 kilogramos y no sobró nada de la cosecha, es decir, se repartió todo en partes iguales y se llegó al mismo resultado que con el dibujo que elaboraste.
Resolver estas divisiones es más fácil que hacer dibujos y llegas al mismo resultado. Podrías hacer otra división para repetir el procedimiento. Anótala en tu cuaderno para que vayas resolviéndola y puedas después repasar. Observa la división.
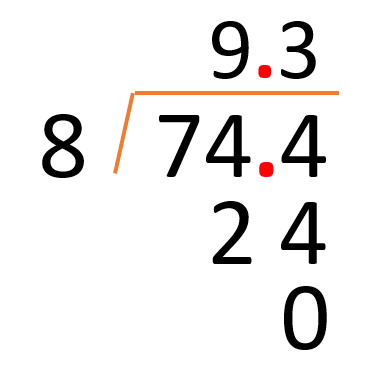
Buscas un número que multiplicado por 8 te dé 74 o un número más cercano, es 9 por 8 que son 72 para 74 son 2. Nuevamente fíjate que ya dividiste la parte entera, así que coloca el punto decimal porque ahora lo que obtendrás serán decimales, entonces tienes 24 entre 8 es 3 por 8 son 24 para 24 es cero. El resultado de esta división es 9 enteros con 3 décimos.
Toma nota de este procedimiento, para que no te veas en la necesidad de solo hacer dibujos, practica algunas otras divisiones como ésta.
Aprender cómo se hacen estas divisiones será útil para cuando te enfrentes a un problema. Observa la relación que existe entre los datos que te dan y qué es lo que te preguntan, porque con base en eso podrás determinar qué operación es la que conviene hacer, es sumamente importante comprender el problema.
Recuerda, siempre que te enfrentes a un problema matemático pon mucha atención en la información que te dan, lo que se pregunta y la relación que existe entre los datos.
El reto de hoy:
Revisa los ejercicios que hiciste y elige uno que puedas compartir con algún familiar cercano, explícale como pudiste obtener tus resultados.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.