Carrera en el tiempo
Aprendizaje esperado: resuelve problemas que implican conversiones entre unidades de medida de longitud, capacidad, peso y tiempo.
Calcula el perímetro y el área de triángulos y cuadriláteros.
Énfasis: resuelve problemas en los que sea necesaria la conversión entre diversas unidades de medida y el cálculo del perímetro y área de triángulos y cuadriláteros.
¿Qué vamos a aprender?
Resolverás problemas que implican conversiones entre unidades de medida de longitud, capacidad, peso y tiempo, calcularás el perímetro y el área de triángulos y cuadriláteros, recordarás los temas que ya habías visto en tus clases de quinto grado.
¿Qué hacemos?
Seguirás en el viaje en el tiempo, hoy tenemos preparada una travesía en la que recordarás temas que estudiaste en quinto grado y por algunas historias que sucedieron hace algunos años y en la actualidad.
¿Ya estás lista y listo para dar inicio?
Antes que nada, debes saber que seguiremos abordando varios temas que ya viste en quinto grado, por ejemplo, las unidades de medida de capacidad, tiempo, áreas y perímetros.
Es normal que, con el paso del tiempo, cuando no practicamos algo lo olvidemos, así que en esta sesión irás recordando todo esto.
Iremos contestando lo más rápido posible algunas preguntas, pero antes de que respondan las preguntas, aparecerá el título del tema al que nos remontaremos en el tiempo, luego haremos un pequeño repaso y al final aparecerá la pregunta.
¿Quedaron claras las instrucciones?
Las instrucciones están claras.
Entonces veamos a dónde viajaremos.

Recordarás las unidades de tiempo, para esto, los invito a ver un pequeño fragmento de una sesión del ciclo escolar pasado.
- #AprendeEnCasa II. 5º Primaria. Matemáticas. A través de los años 29 de octubre 2020
https://youtu.be/OoMFitKStZU?t=403
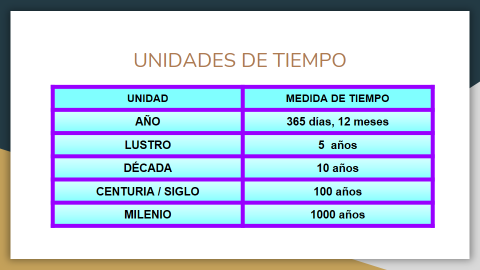
¿Ya recordaste? estás preparada/o para resolver las preguntas.

Como apoyo en la resolución de este problema tenemos la tabla de equivalencias.
¿Cuánto tiempo pasó de 1521 a 1821?
Trescientos años, y como cada siglo tiene cien años, entonces pasaron 3 siglos.
Ahora bien, si cada lustro tiene 5 años entonces podemos dividir 300 entre 5 y el resultado de esta división es 60 por lo que son 60 lustros.
Por último, como cada siglo tiene 10 décadas, entonces han pasado 30 décadas de la conquista de Tenochtitlán.
¿Estás revisando tus respuestas? Nos falta una pregunta, ¿En qué año se cumplirá un mileno?
Deben pasar 1000 años, entonces de 1521 debemos llegar al año 2521 ¡eso es mucho tiempo!
Efectivamente no viviremos tantos años para recordar esa fecha.
Pero como el tiempo corre de prisa, vamos con el siguiente tema por favor.
El siguiente tema es áreas y perímetros.

Recordemos que el perímetro es la suma de todos los lados de un polígono y el área es la medida de la superficie del polígono.
El área es la medida de la superficie de una figura, pero revisemos de nueva cuenta este tema y una vez más dirijámonos al pasado en nuestra nave del tiempo.
Presta atención al siguiente video para que logres responder correctamente el siguiente reto.
- Construimos fórmulas. Del minuto 05:04 al 07:05
https://youtu.be/52W-RoW4WIk?t=304
También contamos con el siguiente material de apoyo para contestar el reto.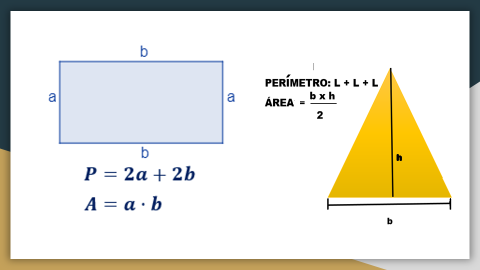
Observa la imagen y escucha con atención en qué consiste el siguiente reto.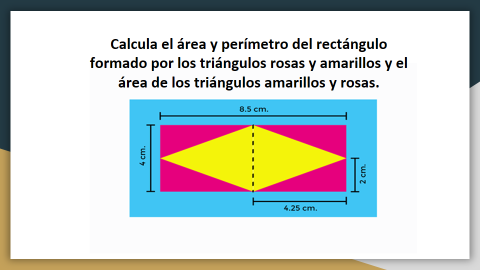
Comienza con el perímetro del rectángulo y éste se obtiene sumando: 8.5 + 8.5 porque son dos los lados largos, pero además sumamos 4 + 4 porque eso miden sus lados cortos, así que obtenemos 8.5 + 8.5 = 17 y le sumamos 8 nos da 25 por lo tanto, el perímetro del rectángulo mide 25 cm.
Ahora para obtener el área debo multiplicar la base por la altura; entonces 8.5 x 4 es igual a 34 punto cero, por tanto, el área del rectángulo mide 34 cm cuadrados, maestra.
Ahora falta calcular el área de los triángulos.
En la imagen nos recordaron que el área de cualquier triángulo se obtiene multiplicando su base por su altura y el producto obtenido se divide entre dos.
¿Tienes todas las medidas para calcular las áreas de los triángulos?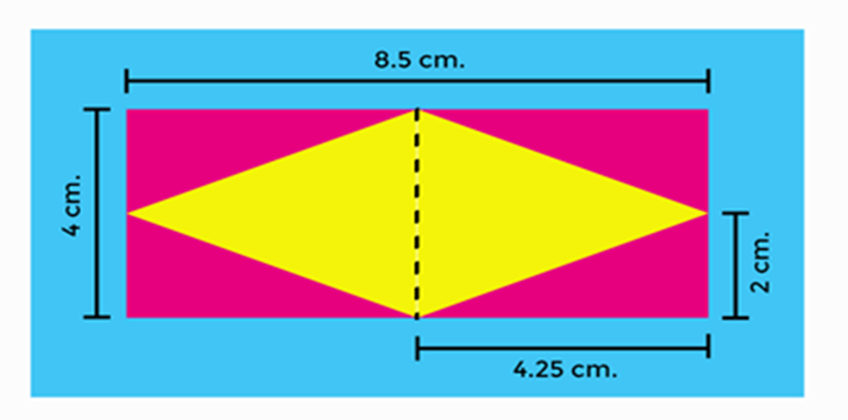
Voy a empezar a analizar los triángulos amarillos. La base mide lo mismo que la longitud del lado corto del rectángulo.
¿Y cuánto mide su altura?
Pues se observa que la altura coincide con la mitad de la medida del lado largo del rectángulo, es decir, que la base mide 4 y su altura 4.25 así que al multiplicarlos obtengo 17 y al dividir esta cantidad entre dos, se tiene 8.5
Entonces el área de cada triángulo amarillo es igual a 8.5 cm cuadrados, porque los dos triángulos son iguales, ahora falta el área de los triángulos rosas.
Pues el área de los triángulos rosas se obtiene de inmediato, ya que su base coincide también con la mitad de lo que mide el lado largo del rectángulo.
¿Y cuánto mide su altura?
Su altura es la mitad del lado corto del rectángulo, así que multiplicamos 4.25 por 2 y esto nos da 8.50 y al dividir esta cantidad entre dos, obtenemos 4.25
Entonces el área de cada triángulo rosa es de 4.25 cm cuadrados, ya que los cuatro triángulos rosas son iguales.
¿Seguiste el proceso? ¿Obtuviste los mismos resultados? Verifícalos por favor y si es necesario solicita ayuda de algún adulto en casa o de tu maestro, también analiza por qué decimos que los 4 triángulos rosas son iguales y, por lo tanto, su área mide lo mismo.
Vayamos en nuestra máquina del tiempo a la siguiente parada.
Hagamos un breve repaso. Vayamos en nuestra nave a la sesión donde vimos esto. - Litros y litros para limpiar. Del minuto 05:04 al 07:05
https://youtu.be/9y3wgEAz-zg?t=1504
Vamos con el siguiente tema: medidas de longitud. ¿Recuerdas cuáles son las medidas de longitud?
El metro es la medida principal y de ahí se derivan los múltiplos y submúltiplos del metro como el kilómetro o el decímetro.
Es importante mencionar que en la actualidad estas medidas se siguen actualizando, incorporando unidades de medida nuevas de acuerdo con las necesidades que exige el progreso científico, por ejemplo, el byte es el elemento mínimo de memoria direccionable de una computadora y mide la capacidad de almacenamiento digital.
Estas nuevas unidades de medida en estos momentos son polémicas y está a discusión si se utilizan como medidas internacionales.
Este sí que fue un viaje en el tiempo, pasamos de pasado al futuro midiendo espacio virtual.
Hemos acabado un viaje más que ha sido largo y fructífero, ya que recordaste las unidades de medida, tanto de longitud, de área, de capacidad y de tiempo, y nos dimos cuenta que, gracias al progreso científico, las necesidades cambian o se redefinen y se requiere ir incorporando nuevas unidades de medida a las existentes, aunque las anteriores siguen siendo vigentes y de gran utilidad.
No dejes de seguir repasando los temas de quinto grado, ya que son la base para los nuevos aprendizajes que vamos a adquirir en este año escolar.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Consulta los libros de texto en la siguiente liga.