Cajas para regalo
Cajas para regalo
Aprendizaje esperado: calcula el volumen de prismas mediante el conteo de unidades.
Énfasis: resuelve problemas que impliquen la idea de volumen de un prisma, como la cantidad de cubos que lo forman.
¿Qué vamos a aprender?
Calcularás el volumen de prismas mediante el conteo de unidades y resolverás problemas que impliquen la idea de volumen de un prisma como la cantidad de cubos que lo forman.
¿Qué hacemos?
El 1 de junio es el día de la marina y fue determinado por el hecho de que el 1° de junio del año de 1917 zarpó del puerto de Veracruz, por primera vez un buque mercante mexicano, el vapor “Tabasco”, con el total de la tripulación compuesta exclusivamente por mexicanos de nacimiento.
Antes de esa fecha, los capitanes, jefes de máquinas y oficiales de los barcos mexicanos eran todos extranjeros.
La primera ocasión en que se celebra el Día de la Marina es el 1° de junio de 1942.
Observa el siguiente video sobre este acontecimiento.

- Video alusivo al Día de la Marina Nacional 2020.
https://www.gob.mx/semar/videos/dia-de-la-marina-nacional-244154
De este video surgen varias preguntas, ¿Será muy difícil transportar los productos en los barcos mercantes? ¿Cómo saber cuánto espacio se dispone para llevar cada carga? algunos barcos que tenían contenedores muy grandes, ¿Cuánto pesarán?
Estas preguntas son interesantes y además hay que considerar los camarotes para la tripulación, el área de máquinas, cocina y otros espacios.
 |
 |
Las preguntas resultan muy oportunas, porque tienen relación con uno de los problemas con los que trabajarás en el desafío 70 se refiere a seleccionar unas cajas para colocar chocolates. Abre tu libro de texto en la página 129 donde está el Desafío 70, “Cajas para regalo”.
https://libros.conaliteg.gob.mx/20/P6DMA.htm?#page/129

La consigna dice lo siguiente:

Analiza la información que te proporciona el problema.

Hay 30 chocolates de forma cúbica. ¿Saben a qué se refiere de forma cúbica? Se refiere a que son como los dados que se usan para jugar, dados pequeñitos.
Ahora en el problema pide encontrar las medidas ideales para una caja que tenga forma de prisma rectangular. Tienes que imaginar cómo debe ser la caja en forma de prisma rectangular, en la cual sea posible acomodar los 30 chocolates.
En tu cuaderno traza las dimensiones que estás identificando, seguramente ya te estás imaginando la caja con sus dimensiones. Pero ahora considera las características de un prisma rectangular. ¿Cuál es su polígono de base? Es un rectángulo.

Traza el polígono de base, el rectángulo, lo cual te ayudará a imaginar cómo debes colocar los chocolates, considerando que cada uno mide 1 cm en todas sus aristas.
¿Cuál es tu propuesta de las medidas de la caja, con lo que estás imaginando? Pues unas medidas posibles son, de largo, mide 5 cm, 3 cm de profundidad y 2 cm de altura.

Ya tienes una propuesta de las medidas para una caja con forma de prisma rectangular. ¿Cómo puedes comprobar que realmente caben los treinta chocolates? Tal vez puedes multiplicar, pero ¿Qué vas a multiplicar? Pues 5 cm de largo por 3 de profundidad. Y 5 por 3 da 15 luego esto lo multiplicas por 2 y 15 por 2 es 30
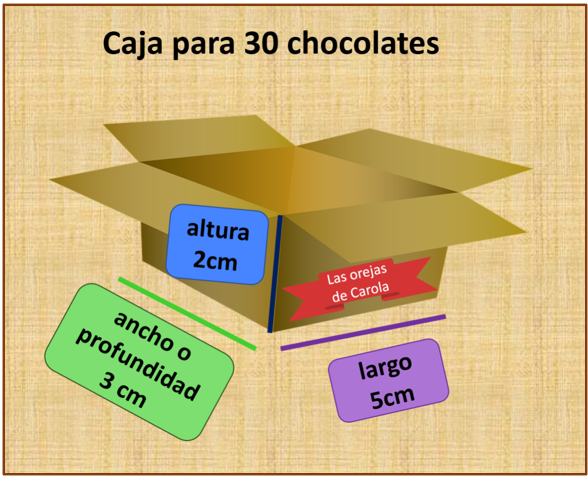
La caja quedó como se observa en la imagen, porque al multiplicar 5 cm de largo por 3 cm de ancho, se obtienen 15 cm cuadrados, o sea 15 cuadros y en cada cuadro puedes colocar un chocolate, al multiplicarlo por 2 cm de altura, estas considerando que tienes dos niveles de 15 chocolates, por lo tanto, en la caja puedes acomodar en total 30 chocolates que miden 1 cm en cada una de sus aristas. Con esto compruebas que la propuesta de esas medidas de la caja es correcta.
¿Pueden ser las únicas medidas? Tal vez la caja también puede medir 5 cm de largo, 2 cm de ancho o profundidad y 3 cm de altura. Quedaría así y las medidas de sus dimensiones cambian, así que ya no es igual que la primera caja, pero seguirá conteniendo 30 chocolates en forma de cubos con 3 cm de arista.
Las medidas de esa segunda caja son 5 cm de largo, por 2 cm de ancho o profundidad es igual a 10. Ahora 10 por 3 de altura es igual a 30 así que el volumen de esta caja también es de 30 cm cúbicos. Lo que significa que en esta caja también caben 30 chocolates en forma de cubos de un centímetro de arista.
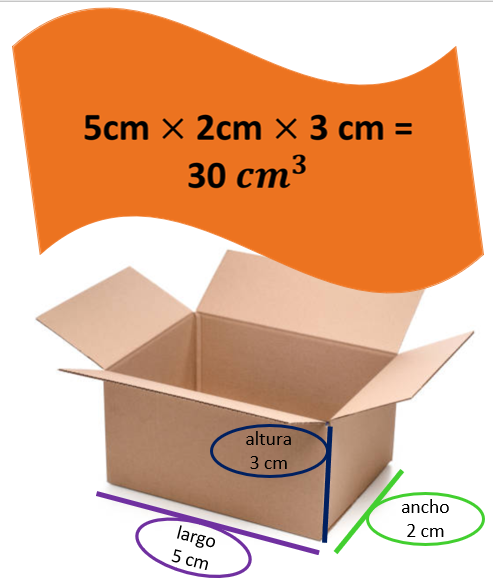
¿Se te ocurren otras medidas que permitan acomodar los 30 chocolates en una caja con forma de prisma rectangular?
Pasa ahora al problema del inciso “b”.

¿Crees que se pueda tener una caja de forma cúbica para los 30 chocolates? Recuerda que forma cúbica significa que la caja debe medir lo mismo en sus aristas. ¿Cómo serían las medidas de largo, ancho y altura?
Seguramente imaginas que esa caja, sería como un dado grande, por lo tanto, su largo, ancho o profundidad y altura tienen que medir lo mismo, ¿Crees que se pueda encontrar una caja para la cual sus dimensiones deberán tener la misma medida? Si lo reflexionas, no hay un número que multiplicado por sí mismo tres veces, de 30
¿Por qué un número multiplicado por sí mismo tres veces? Porque si la caja es cúbica debe medir lo mismo en todas sus aristas y, al multiplicar tres veces el mismo número, estás multiplicando las tres dimensiones de la caja, el largo, el ancho y la altura.
¿Hay un número que multiplicado por sí mismo tres veces sea igual que 30? Escribe las medidas posibles para las tres dimensiones de la caja cúbica. Puede ser…
2 x 2 x 2 = 8
3 x 3 x 3 = 27
El resultado se acerca, pero con el siguiente número que es 4 se pasa.
4 x 4 x 4 = 64
Aquí puedes observar que no se encuentra un número entero que multiplicado por sí mismo tres veces, dé exactamente 30 entonces, ¿Cuál es tu conclusión? Que no hay una caja de forma cúbica en la que se puedan acomodar 30 chocolates que tengan esas medidas, ahora escribe las respuestas en tu libro de texto, de acuerdo con lo que estuviste analizando.
Resuelve la actividad 2 del desafío.

Observa la imagen en grande para que te sea más sencillo.
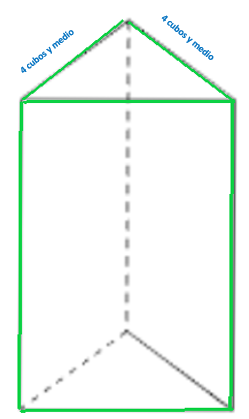
Es un prisma triangular, porque la forma del último nivel es un triángulo, por lo tanto, su primer nivel, la base, tiene forma de triángulo, aunque sólo se puede observar la parte superior del prisma, además, también se puede ver una de las tres caras laterales tiene forma de rectángulo.
Bien, ya identificaste cuáles son las figuras planas que forman al prisma triangular de la imagen. ¿Cómo puedes calcular su volumen? Este problema es más complicado, porque hay cubitos partidos a la mitad, pero si usas tu imaginación espacial como antes, podrás resolverlo.
Explora la estrategia siguiente. Las bases son triángulos que miden en dos de sus lados 4 cubos y un medio. Completa un cuadrado haciendo otro prisma igual al prisma original, luego lo pegas de manera que las bases formen un cuadrado, así que cada cuadrado tendrá 5 cm de lado.
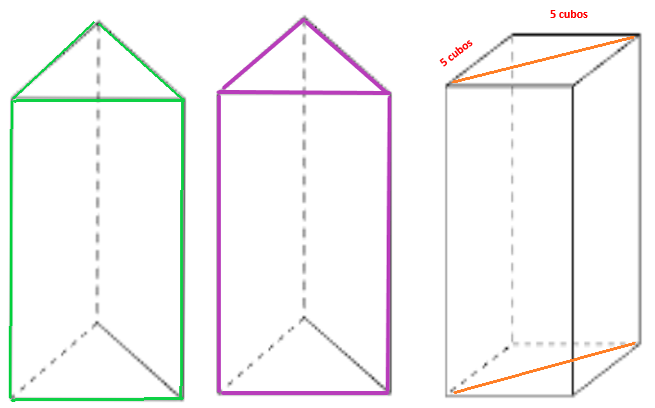
Entonces, si construyes la base de un prisma cuadrangular de 5 por 5 cubos, es decir, ahorita con 25 cubos como área de la base del nuevo prisma cuadrangular, ya tienes dos dimensiones del prisma, solo te falta una.
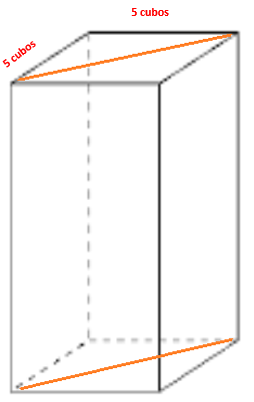
Observa que no cambió la altura del prisma triangular original, ésta sigue siendo 6
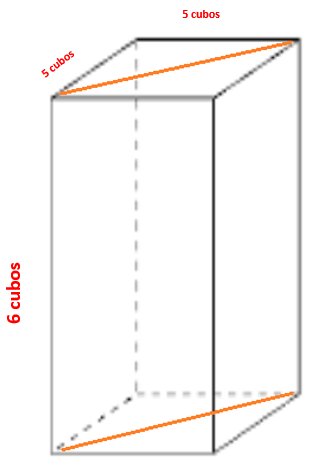
Entonces para terminar de calcular el volumen o la cantidad de cubos iguales que tiene este nuevo prisma, lo único que falta es repetir seis veces la base cuadrangular (que es lo que mide la altura del prisma original) o de manera más fácil, multiplicar el área que tiene la base por la altura del prisma, así que tienes:
25 x 6 = 150
Esa es la cantidad de cubos que tiene el prisma cuadrangular, y como el que te piden es la mitad de éste, entonces divide entre dos el volumen que acabas de obtener y de esa forma ya sabes cuántos cubos tiene el prisma triangular original:
150 / 2 = 75
El prisma triangular original está formado por 75 cubos.
Estos ejemplos te ayudan a entender mejor que el volumen es el espacio que ocupa un cuerpo y que utilizando cubos de igual tamaño puedes medir con mayor facilidad esta característica de los cuerpos geométricos.
Los cubos ejemplifican muy bien, pero cuando son muchos es muy difícil contarlos todos, entonces puedes recurrir a la multiplicación para hacerlo más sencillo. No olvides que para los prismas triangulares puedes también usar la división, ya que resulta mejor dividir que contar mitades, lo cual puede hacer que pierdas la cuenta y equivocarte en el resultado.
Como te diste cuenta, has usado medidas lineales de cada una de las dimensiones que tiene un prisma, en los ejemplos de las cajas las medidas lineales fueron: largo, ancho y altura.
Para facilitar los cálculos, después recurriste a la multiplicación de la medida de cada dimensión para encontrar el volumen del cuerpo geométrico.
También te diste cuenta, en el último problema, que puedes recurrir a tu imaginación para encontrar una estrategia que te permita calcular el volumen de un cuerpo geométrico que no sea fácil de calcular.
Puedes apoyarte en tu imaginación para buscar estrategias y llegar a los resultados.
El reto de hoy:
Comparte con un familiar cercano alguno de los ejercicios que más te haya agradado y explícale como lo resolviste.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
