¡Todo en la misma proporción!
¡Todo en la misma proporción!
Aprendizaje esperado: resuelve problemas de proporcionalidad directa e inversa y de reparto proporcional.
Énfasis: enunciar las características de la proporcionalidad directa, mediante el uso de una tabla, de la expresión algebraica y de la constante de proporcionalidad.
¿Qué vamos a aprender?
Reconocerás las características de una tabla de variación de proporcionalidad directa, así como su constante de proporcionalidad. Además, profundizarás en problemas de proporcionalidad directa donde falta algún valor y conocerás cómo resolver problemas de reparto proporcional.
Para avanzar en tu aprendizaje, también estudiarás las características de la proporcionalidad inversa, distinguirás sus diferencias con la proporcionalidad directa y finalmente resolverás problemas. Asimismo, estudiarás qué es una constante de proporcionalidad.
¿Qué hacemos?
Empieza con una lectura para descubrir los detalles numéricos que te rodean. Lee un extracto de “Los viajes de Gulliver”, del autor inglés Jonathan Swift.
Los viajes de Gulliver
…sus grandes telescopios no exceden de tres pies, aumentan mucho más que los de cien yardas que tenemos nosotros, y al mismo tiempo muestran las estrellas con mayor claridad. Esta ventaja les ha permitido extender sus descubrimientos mucho más allá que los astrónomos de Europa, pues han conseguido hacer un catálogo de diez mil estrellas fijas, mientras el más extenso de los nuestros no contiene más de la tercera parte de este número.
Asimismo han descubierto dos estrellas menores o satélites que giran alrededor de Marte, de las cuales la interior dista del centro del planeta primario exactamente tres diámetros de éste, y la exterior, cinco; la primera hace una revolución en el espacio de diez horas, y la última, en veintiuna y media; así que los cuadros de sus tiempos periódicos están casi en igual proporción que los cubos de su distancia del centro de Marte, lo que evidentemente indica que están sometidas a la misma ley de gravitación que gobierna los demás cuerpos celestes.
Los viajes de Gulliver
(Fragmento)
Jonathan Swift
Leer activa tu imaginación, te da la oportunidad de conocer otros mundos, como a Gulliver en sus viajes. Y si pones atención a la lectura, notarás la presencia de las matemáticas en varios momentos.
Ahora profundizarás en la utilidad de una tabla de datos para establecer la relación entre dos magnitudes.
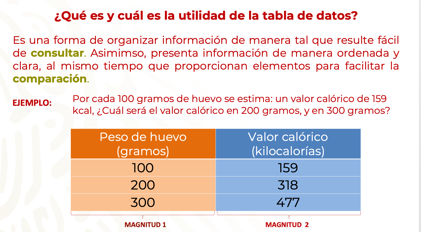
Analiza con mayor detalle la información contenida en esta tabla de datos. Las kilocalorías son la energía que necesita el cuerpo para vivir. Para desarrollar tus funciones vitales, debes incorporar cada día alimentos que te aporten energía. La Organización Mundial de la Salud, OMS, recomienda, para una persona entre los 14 y 18 años, consumir de 2000 a 2300 kilocalorías diarias. En la tabla se puede ver el valor calórico del huevo por cada 100 gramos, es decir: por cada 100 gramos de huevo se tiene un aporte calórico de 159 kilocalorías.
Hay dos magnitudes relacionadas:
La primera magnitud, corresponde a la cantidad en gramos de huevo y la segunda magnitud corresponde al valor calórico en kilocalorías.
La razón, es la relación entre dos magnitudes que son comparables, y que pueden ser de la misma naturaleza o no.
Una tabla de datos es útil para establecer razones entre las magnitudes involucradas, y permite compararlas.
La primera razón:
Por cada 100 gramos de huevo hay un aporte calórico de 159 kilocalorías.
La segunda razón:
Por cada 200 gramos de huevo hay un aporte calórico de 318 kilocalorías.
¿Qué es lo que sucede al comparar las dos razones?
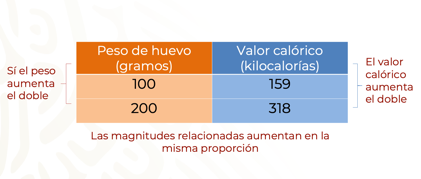
Cuando aumenta la cantidad en los gramos de huevo, aumentará la cantidad en el valor calórico en la misma proporción, en este caso al doble. Es por esta característica que se establece una relación de proporcionalidad directa: el aumento de una magnitud produce el aumento de la otra magnitud, en la misma proporción.
El doble de 100 gramos de huevo, en este caso son: 200 gramos. Le corresponde un valor calórico del doble de 159 kcal. Que serían 318 kcal. Entonces se dice que al doble de gramos le corresponde el doble del valor calórico, kilocalorías.
Es útil hacer uso de las tablas de datos, porque permiten comparar relaciones entre los datos; en este caso, de razones de proporcionalidad. Y en la vida diaria, una tabla de datos -como esta- te permitiría saber cuántas calorías estas consumiendo, por ejemplo.
Si los gramos de huevo aumentan, también aumenta el valor calórico en la misma proporción. A este tipo de relación, en la que una magnitud influye en otra, se le determina como una relación de proporcionalidad.
Pero ¿qué es la proporcionalidad?
La proporcionalidad directa se define como la relación entre cuatro cantidades.
Cuando una de las magnitudes cambia, la otra se modifica en la misma proporción.
Si una aumenta, la otra aumenta también proporcionalmente, y si una disminuye, la otra también lo hace guardando la proporción.
Ahora, analiza una situación que te servirá para comprender mejor el concepto de variación proporcional:
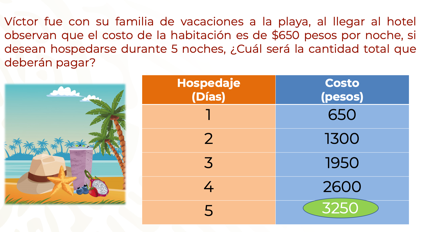
En la tabla se pueden observar los datos organizados de la relación entre la cantidad de días y el costo correspondiente en pesos.
En el problema, la magnitud 1 es representada por la cantidad de días de hospedaje y la magnitud 2, por el costo en pesos por cada día de hospedaje. En esta situación se presenta una relación de dos magnitudes o razones.
El costo de la habitación por cada día de hospedaje es de $650. Si Víctor y su familia se quedan cinco días el costo aumentará.
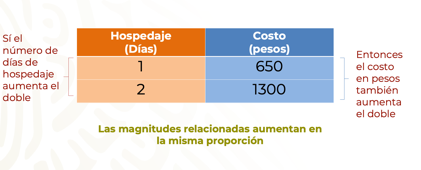
Si los días de hospedaje aumentan, también aumenta el costo, en la misma proporción. Por lo tanto, existe una relación de proporcionalidad entre 4 cantidades, el aumento de los días de hospedaje tiene una relación directa en el aumento del costo.
En esta situación observaste una relación de proporcionalidad directa.
A continuación, analiza otras características de la tabla o registro tabular, usando de ejemplo las vacaciones de Víctor.
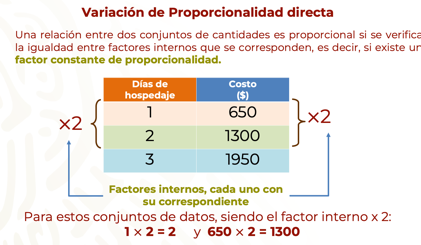
Si se multiplica por dos: El aumento entre los días de hospedaje y el costo aumentaron en la misma proporción, en este caso al doble.
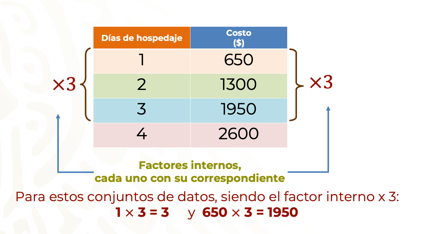
Por tres: El aumento entre los días de hospedaje y el costo aumentaron en la misma proporción, en este caso al triple.
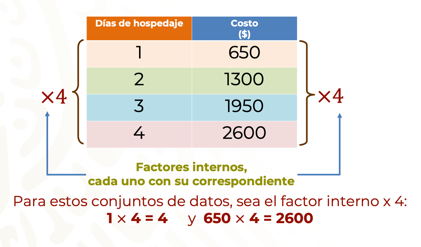
Por cuatro: El aumento entre los días de hospedaje y el costo aumentaron en la misma proporción, en este caso al cuádruple.
Ya sabes que al doble le toca el doble, al triple le corresponde el triple y así sucesivamente. Por lo tanto, la familia de Víctor pagará el quíntuple. Y al número que multiplica a ambas magnitudes se le llamará: factor interno.
Ahora, analiza otras características de la tabla o registro tabular. Siguiendo con la relación hospedaje – días.
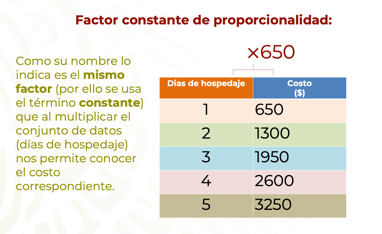
Después de haber comprendido el concepto de factor constante de proporcionalidad, observa otros dos ejemplos:
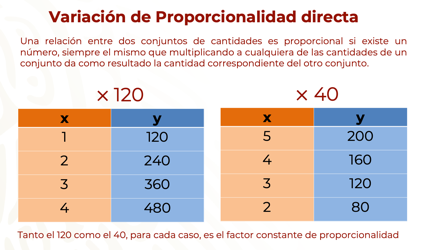
Ahora, observa la formalización de las características estudiadas.
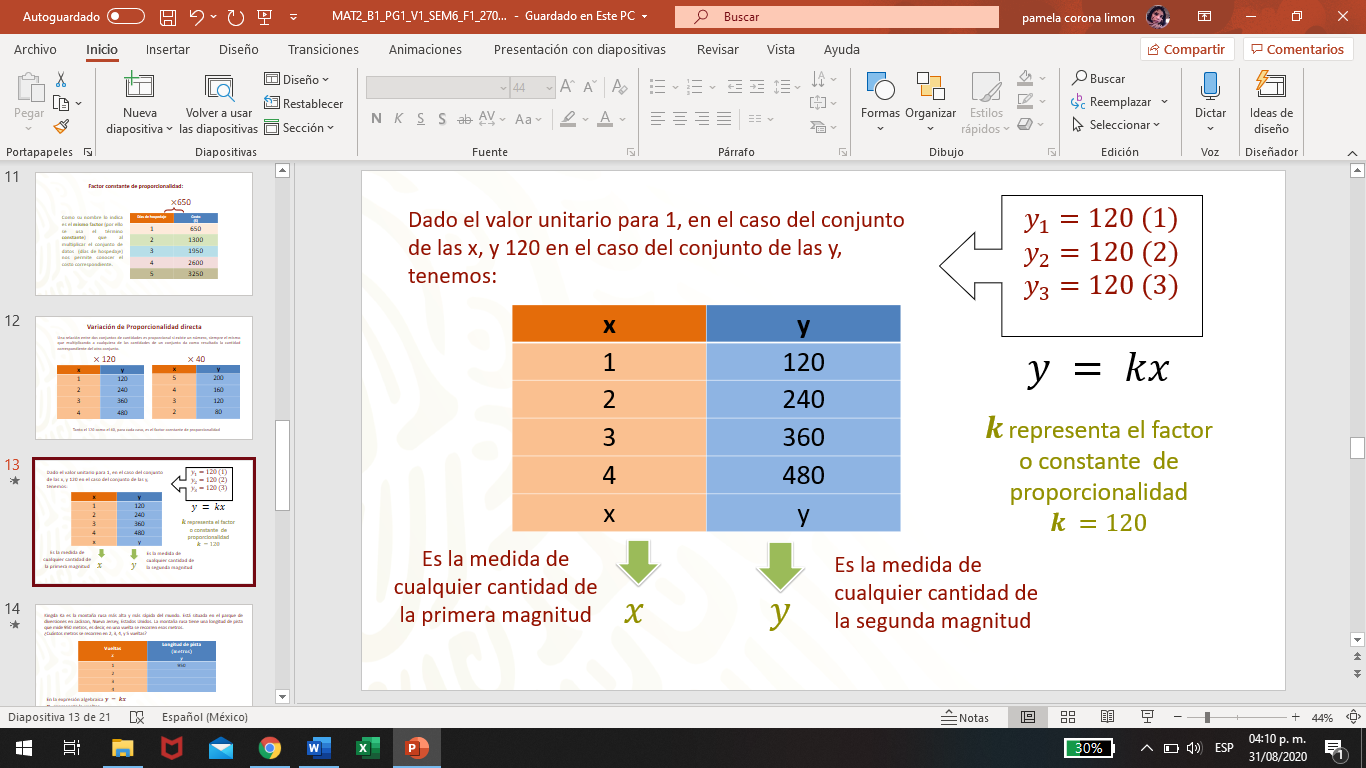
Hasta ahora, has estudiado las características de la variación proporcional, en particular de la variación de proporcionalidad directa.
Realiza la siguiente actividad.

Con esta información, determina los valores y completa la tabla.

En esta situación se presentan dos magnitudes, el número de vueltas, que se representa con “x” y los metros recorridos, que representados con “y”.
Además, la constante de proporcionalidad que se representa con “k” y que aún no se conoce. Recuerda que la constante de proporcionalidad determina el valor de la magnitud correspondiente.
Al conocer ciertos datos correspondientes a las magnitudes, se pueden determinar otros datos faltantes.
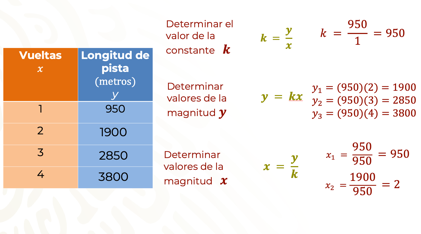
Para calcular el valor de la constante, se divide un valor de “y” con su correspondiente en “x”. Por ejemplo, cuando y= 950 y x= 1, entonces k= 950.
Para determinar valores en “y”, se multiplica su correspondiente en “x” por k, ya determinado su valor, en este caso 950. De esta manera se determina que, si x representa los números de vueltas, su valor es 2, siendo el valor de y = 1900, cuando x = 3, y = 2850 y si x= 4, y= 3800.
Para determinar valores de “x2”, se divide “y2” entre la constante k = 950. Así, si se conoce la longitud de pista, se divide 1900 que es “y2”, entre 950 que es “k” y se obtiene a “x2”, que representa el número de vueltas, en este caso: 2.
Ahora irás de compras, analiza dos listas de precios de un mismo artículo en dos locales. En uno de ellos los artículos se pueden adquirir tanto en menudeo como en mayoreo.
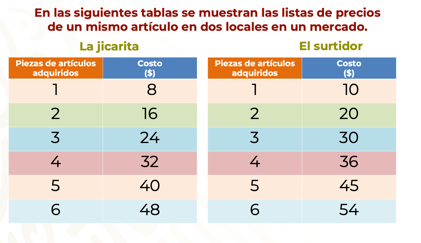
¿Qué identificaste en los precios y en la cantidad de artículos adquiridos?
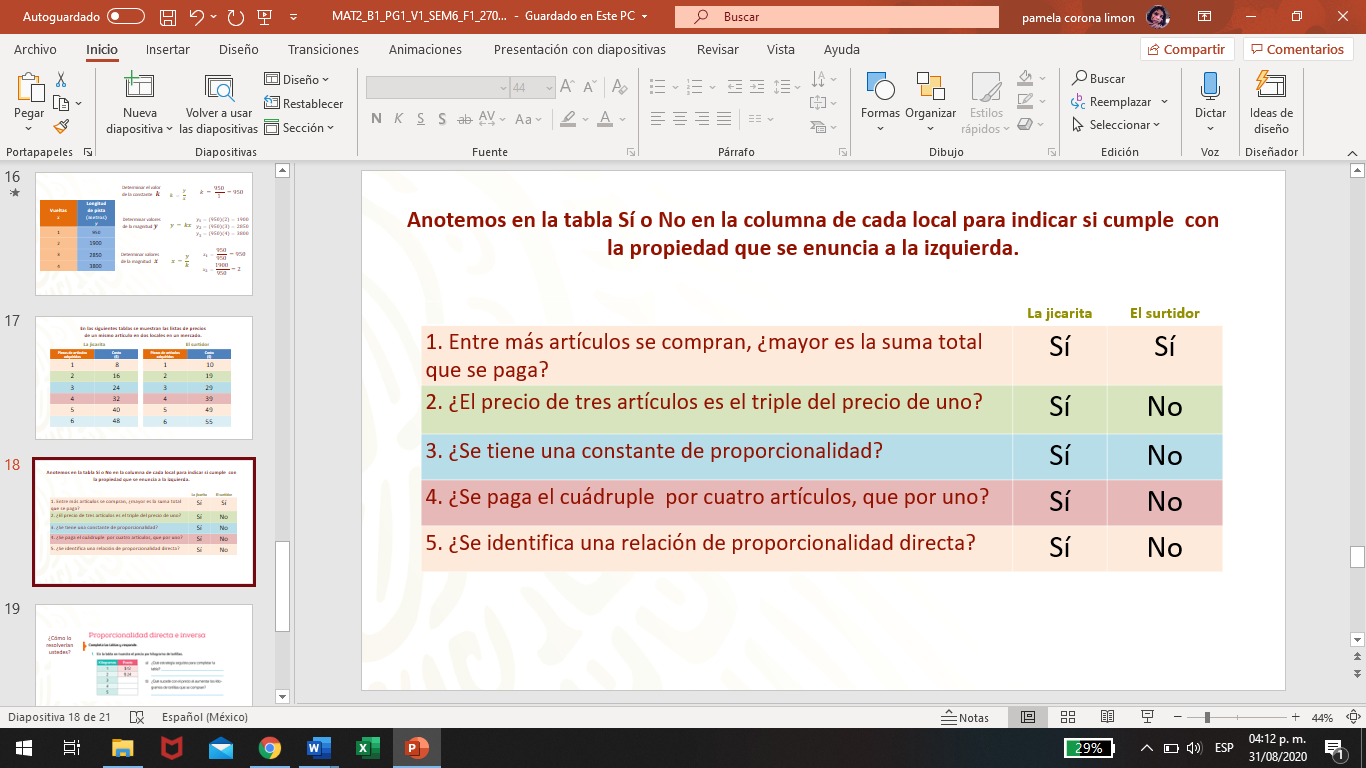
Para 1, efectivamente en ambos locales, entre más artículos se compran, mayor es la suma total que se paga, pero ésta no es una característica suficiente para determinar que hay una relación de proporcionalidad directa.
Para 2, en el local La jicarita, al aplicar el factor interno (que es 4), se identifica que:
1 x 4 = 4 y 8 x 4 = 32, es decir, por cuatro artículos se paga el cuádruple, en relación con la compra de un artículo.
Pero en el caso del local El surtidor, no se tiene el mismo factor interno, ni el factor constante de proporcionalidad, porque la relación entre la adquisición de un artículo por 10 pesos, y 4 artículos por 39 pesos no es proporcional.
Para 3, en el caso del local La jicarita la constante de proporcionalidad es 8, porque siempre que se multiplique la cantidad de piezas por 8, se obtendrá el precio total cuidando la proporción.
En el caso del local El surtidor, no hay una constante debido a que el factor no es el mismo para cada caso.
Para 4, en el caso del local La jicarita los datos de la columna “piezas de artículos adquiridos” están relacionados proporcionalmente con los datos de la columna “costo” y cumple con tener un factor constante de proporcionalidad, (k = 8); sus razones o factores internos son iguales; la razón entre 1 y 8 es la misma que ente 2 y 16. También se puede decir que: el costo es proporcional a la cantidad de piezas de un artículo. Esto significa que el costo por pieza es constante.
En el caso el local B, los datos están en una relación aditiva. No tiene sentido decir que 2 piezas están en relación proporcional, porque se pagan 19 pesos. Para que tenga sentido hablar de proporcionalidad es necesario que haya al menos 4 cantidades en juego: dos que se relacionan con otras tantas.
Continuando con este tema, pon atención en el siguiente ejemplo.
Dos alumnos comenzaron a trabajar con un problema de su libro de texto. Cada uno de ellos usó una forma diferente de resolverlo. Observa cuál era el problema:

Ahora, pon atención en cómo lo resolvió el alumno 1.
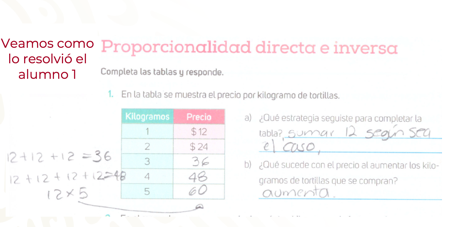
El alumno 1 sumó el precio de un kilogramo de tortillas según los kilogramos solicitados. Para conocer el precio de los 5 kilogramos de tortillas se dio cuenta que con la multiplicación 12 x 5 obtendría el costo. Él identificó que hay un factor constante, que es 12. En su respuesta del inciso b, identifica que tanto los kilogramos de tortillas como el costo aumentan, pero no dijo cómo es ese aumento.
Observa cómo lo resolvió el alumno 2.

El alumno 2, estableció 2 razones o una proporción para compararlas e identificó que hay un factor constante, que es 12. En su respuesta del inciso b, identifica que tanto los kilogramos de tortillas como el costo aumentan en la misma proporción.
Ahora tú, resuelve el ejercicio y encuentra el factor constante y el aumento proporcional.
En esta clase aprendiste situaciones que seguramente en tu vida diaria has tenido la oportunidad de observar: la proporcionalidad, sus elementos y características de proporcionalidad directa; así como los procedimientos para determinar datos faltantes.
Puedes consultar tu libro de Texto Gratuito de Matemáticas de segundo grado para repasar lo referente a la variación de proporcionalidad directa.
El reto de hoy:
Pon a prueba tu imaginación, piensa en alguna situación de tu vida diaria en donde hayas identificado un ejemplo de variación de proporcionalidad directa. Y anótalo en tu cuaderno.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/