Geometría
Geometría
Aprendizaje esperado: concibe las matemáticas como una construcción social en la que se formulan y argumentan hechos y procedimientos matemáticos.
Énfasis: vincular conceptos fundamentales.
¿Qué vamos a aprender?
Para esta sesión se han preparado una serie de consideraciones respecto al vínculo entre los elementos y contenidos geométricos, cuyo aprendizaje se promueve a lo largo de la educación básica.
Aprenderás la importancia que representa comprender y apropiarse de los saberes geométricos, para utilizarlos como herramientas al resolver situaciones tanto matemáticas, como de otros ámbitos del conocimiento.
De este modo, se vincularán conceptos fundamentales de la geometría.
Los materiales que utilizarás son tu cuaderno de notas, un bolígrafo, un lápiz y una goma.
Procura registrar tus dudas, inquietudes y anotaciones respecto a los contenidos que se presentan.
¿Qué hacemos?
En materia educativa, se considera un desacierto pensar que la mente infantil es como una hoja en blanco en la que se pueden escribir los aprendizajes.
La mente humana atraviesa por muchas y diversas etapas de desarrollo que se deben considerar al organizar los aprendizajes y la actividad educativa, de este modo ya has transitado por diversas etapas en tu propio desarrollo.
Por ende, no resulta extraño escuchar que las nuevas generaciones comienzan a manipular a edades más tempranas equipos sofisticados de tecnología.
Antes de la edad preescolar, has sido capaz de encontrar material audiovisual como videos, pasar el rato jugando o descubriendo nuevas imágenes desde la pantalla de un teléfono o cualquier dispositivo con una conexión a internet.
Sin embargo, la información a la que se tiene acceso debe cobrar sentido para incorporarse a la estructura de los conocimientos necesarios y enfrentar así las situaciones que desafían el intelecto.
Y como ya se ha mencionado, muchas de esas situaciones se te ofrecen en el ámbito escolar.
Es por ello por lo que, a lo largo de la sesión, se ejemplifica la importancia de elementos básicos para dar sentido al planteamiento de vincular conceptos fundamentales para el estudio de la geometría con una serie de consideraciones.
La primera es relativa a un segmento de recta.
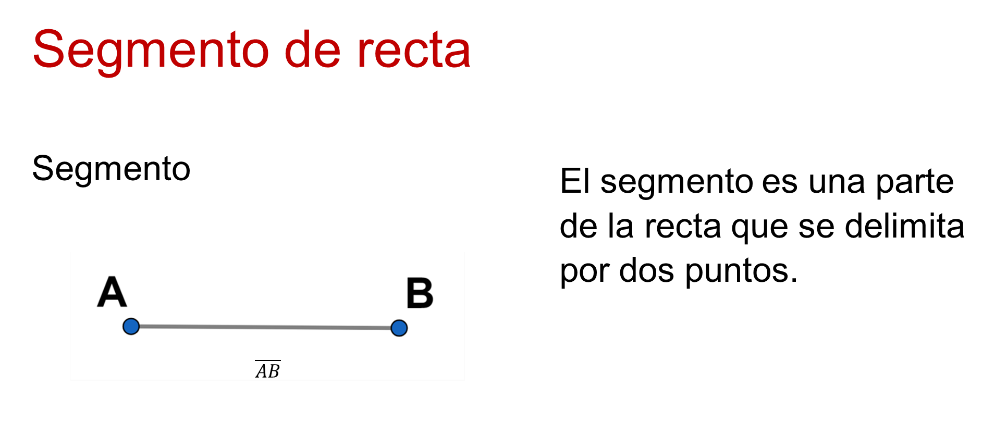
Un segmento no es lo mismo que una recta. El segmento, es una parte de la recta que se delimita por dos puntos y que, para denotar al segmento, se etiquetan los puntos que son sus extremos.
En la imagen, se tiene el segmento “AB”. El segmento cobra significado paulatinamente en construcciones, figuras y cuerpos geométricos.
Por esta misma razón, comprender los conceptos fundamentales va más allá de memorizar su definición. Se trata de darles sentido para incorporarlos con oportunidad y eficiencia en el momento necesario, por ejemplo, al resolver situaciones escolares o de la cotidianeidad.
En los primeros años escolares, un lápiz se puede asociar al concepto de segmento de recta, representando como sus extremos la punta de grafito y la goma.
La intención es motivar los procesos reflexivos en los que se asocian conceptos con objetos o situaciones que les son representativos a esa edad, y que forman parte de retos escolares más demandantes.
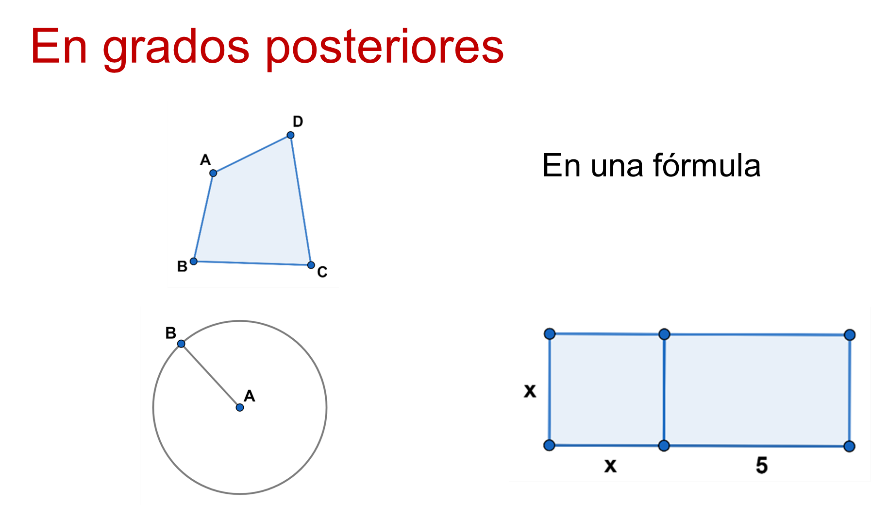
De este modo, en los grados escolares posteriores, el segmento de recta se identifica en cada lado de un polígono.
Este puede adquirir sentido al aparecer como una variable en la fórmula del perímetro de un polígono regular, denotado con la letra “L”, o como el radio de una circunferencia.
Otro ejemplo está, en una de sus expresiones más sofisticadas, los lados de un rectángulo cuya medida se desconoce.
¿Cómo un concepto que parece tan básico puede afectar el aprendizaje en tercer grado de secundaria?
Para responder se tiene la siguiente situación.
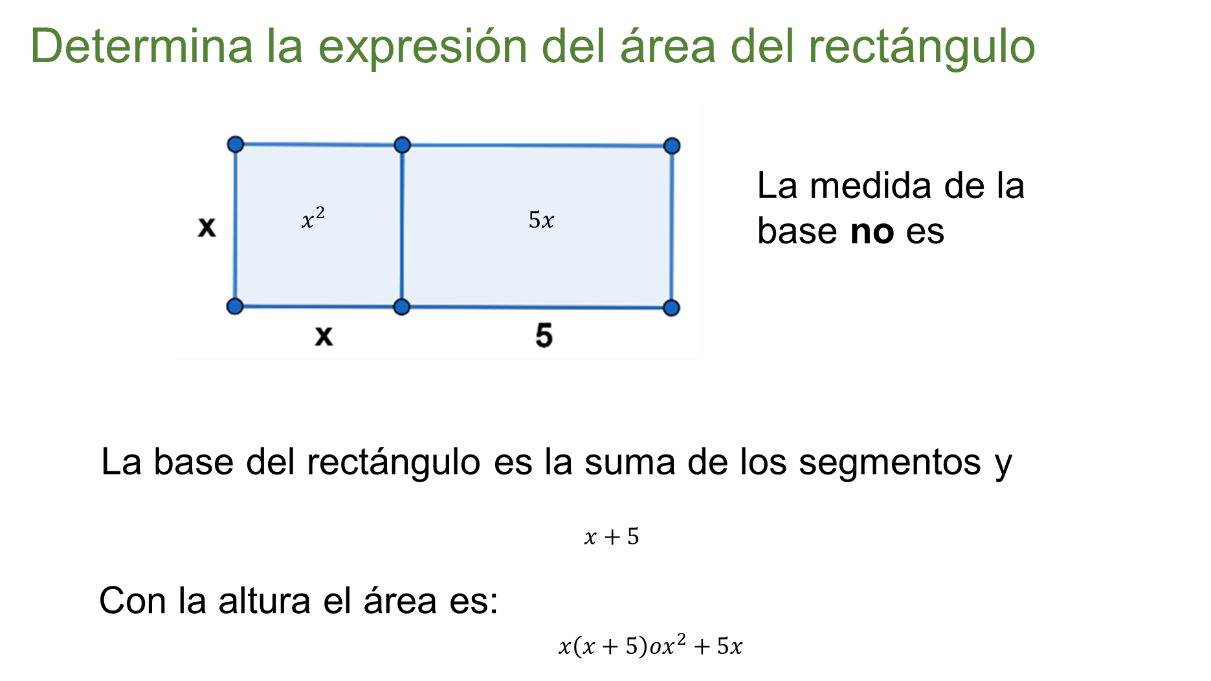
Un error común al expresar el área o el perímetro de un rectángulo como este, es suponer que la longitud de la base tiene por medida “5x”.
En muchas ocasiones, al enfocarse en el aprendizaje de sumas algebraicas, productos notables o las ecuaciones de segundo grado, se pierde de vista que la base del rectángulo está formada por dos segmentos de recta; uno de medida “x” y otro de medida 5. Por lo que la medida de la base es la suma de las medidas de los segmentos, “x” más 5.
Su área se expresa como “x” por “x” más 5 que simplificado es “x” al cuadrado más “5x”.
Como ya se ha hecho notar, cada concepto, aprendizaje y habilidad, forma parte de una estructura que da solidez al desarrollo del pensamiento matemático.
El nivel de dificultad de la actividad matemática escolar es progresivo, pero se sustenta en la articulación de esos conceptos fundamentales.
Observa un ejemplo más de la importancia del concepto de segmento de una recta.
Se intenta plantear la proporción que representa la semejanza de los triángulos, y para este caso, se requiere formar la proporción correcta de los segmentos correspondientes.
Considerando que la proporción es una igualdad entre dos fracciones, y por la referencia con otros ejemplos, de manera instintiva se buscan los términos que deben ocupar los 4 lugares.
Por esta razón, es común encontrar como respuesta 12 entre 7 es igual a “x” entre nueve.
Sin embargo, los segmentos no se corresponden “uno a uno” como lados de los triángulos semejantes.
El lado del triángulo mayor es la suma de los otros segmentos, uno de medida 9 y otro de medida “x”, por lo que la expresión correcta debe incluirlos.
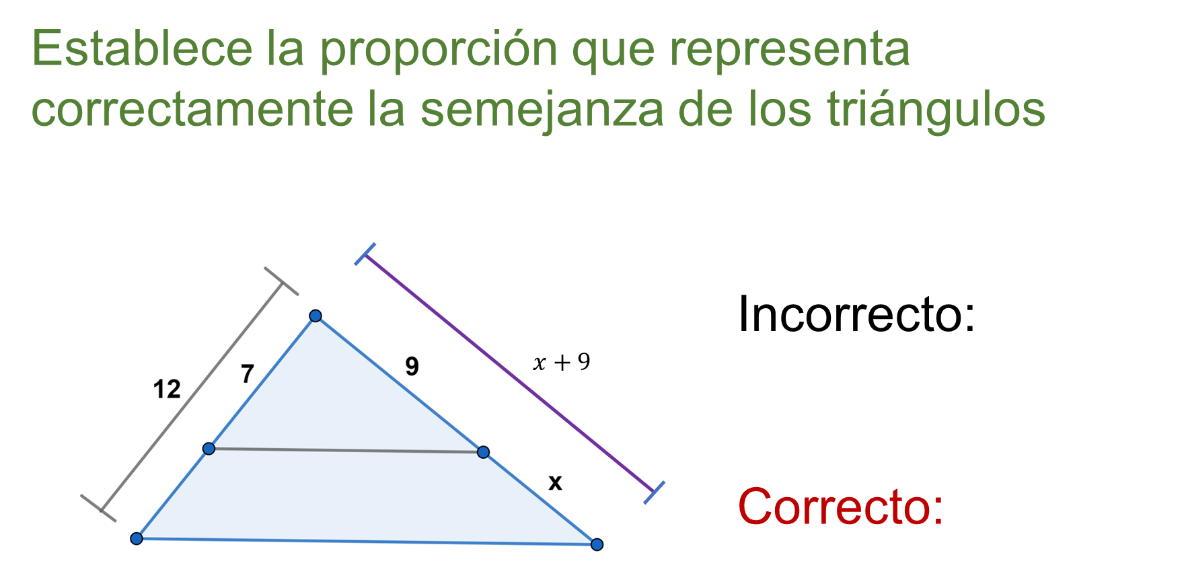
Un error así es menos probable cuando se ha tenido ocasión de consolidar y validar un concepto fundamental como lo es el segmento de recta. Aunque, también cuentan las proporciones y semejanza de triángulos.
Los conceptos fundamentales no representan elementos aislados en la geometría. Por el contrario, se incorporan a una extensa red de saberes que, al vincularse, potencian la capacidad de abstracción y razonamiento para resolver cada situación dada, y en particular, las que tienen que ver con las matemáticas.
Estos son los conceptos que se involucran en las situaciones a medida que se accede a grados superiores, y que, de igual modo, forman parte de la estructura de conceptos que fortalecen el pensamiento lógico deductivo.
Explora otros conceptos fundamentales, perpendicularidad y paralelismo.
Dos rectas son perpendiculares si su intersección genera ángulos rectos de 90 grados.
Los segmentos y semirrectas que forman ángulos de 90 grados también son perpendiculares.
Es necesario conocer la clasificación de los ángulos por su medida, recto, agudo y obtuso.
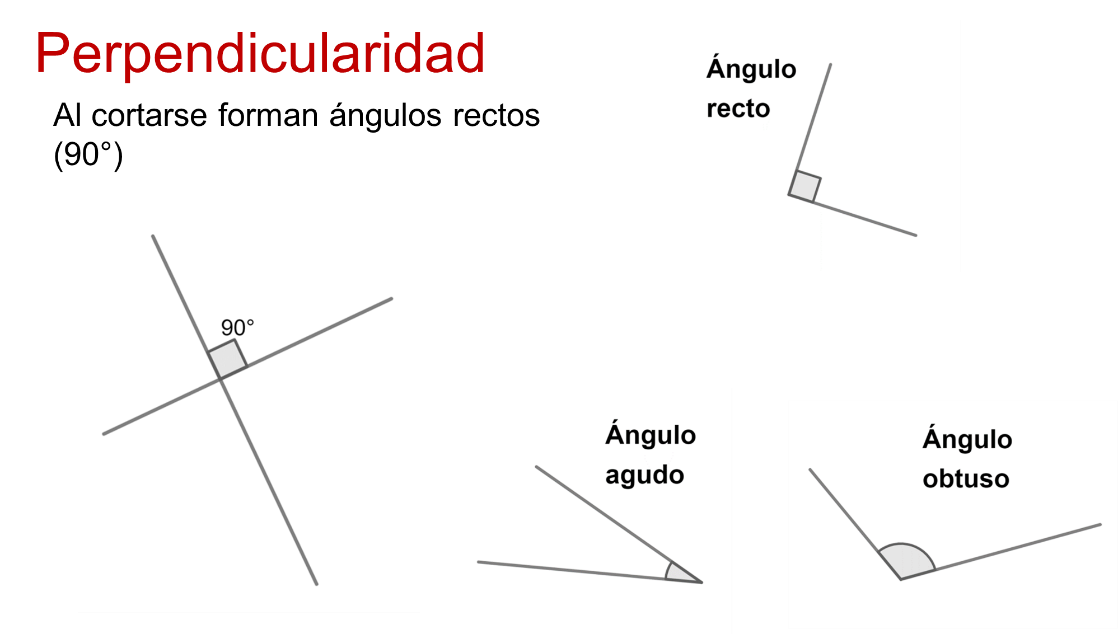
En un primer acercamiento, has podido asociar a los ángulos con la apertura entre las hojas de las tijeras, las manecillas del reloj, con las esquinas del pizarrón o de un cuaderno, por mencionar algunas.
A medida que accediste a grados superiores, clasificaste distintos ángulos e identificaste al ángulo recto como el más común en el entorno y el que define las características de las figuras geométricas más comunes, el cuadrado y el rectángulo.
En un comienzo, clasificaste los ángulos como “mayores que un ángulo recto” o “menores que un ángulo recto”, después aprendiste a denominarlos por sus nombres, “obtusos” y “agudos”.
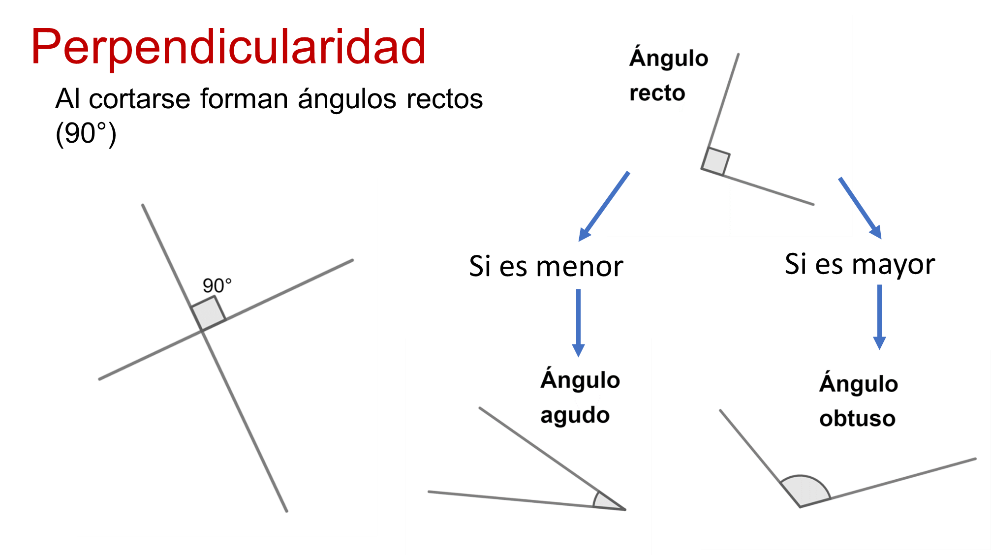
Los segmentos perpendiculares siguen presentes en la altura de los triángulos, paralelogramos y trapecios. Seguro reconoces la base y altura de las figuras.
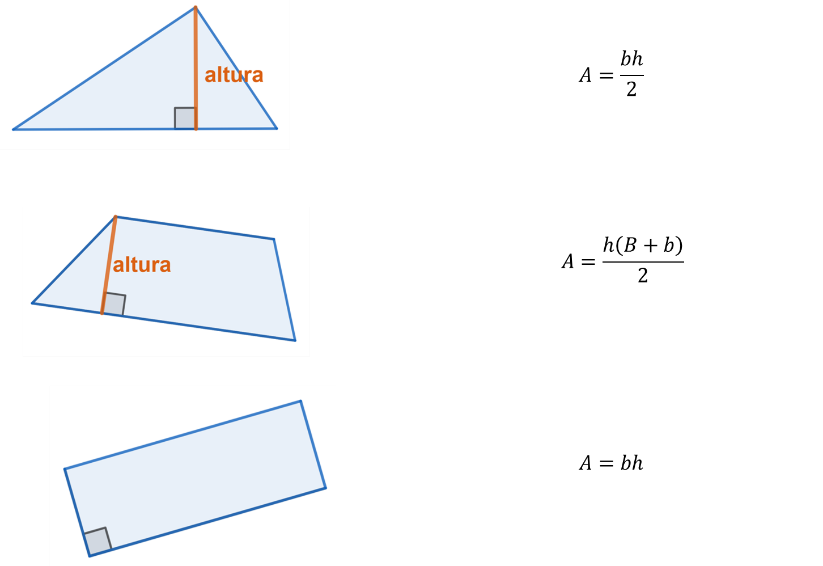
Pero estos segmentos van cobrando sentido como elementos que después parecen comunes en las fórmulas para calcular el área de las figuras básicas.
En las primeras oportunidades, suele generar confusión determinar la altura de un triángulo o la de un trapecio. Sin embargo, la experiencia al estudiar rectángulos —el cuadrado también es un rectángulo—, plantea que la base es indistintamente, un lado de la figura y la altura el lado contiguo.
Si la idea de la perpendicularidad de la altura no es sólida, se puede confundir la altura de un triángulo con uno de sus lados.
Por ello, en grados superiores los errores no se deben siempre a contenidos sofisticados como trigonometría, Teorema de Pitágoras o la semejanza de triángulos. En muchas ocasiones, el obstáculo es una asimilación incompleta de los conceptos básicos de geometría.
Considera ahora que la apotema de un polígono regular es un segmento que va desde el centro del polígono al punto medio de cualquiera de sus lados, siendo perpendicular a éste.
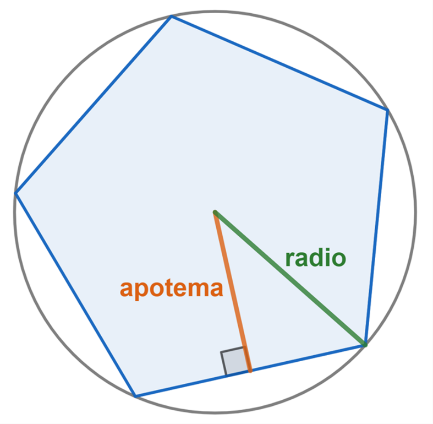
Como se puede observar, existe una diferencia en la longitud de la apotema y el radio de la circunferencia circunscrita al polígono.
Si no se establece con claridad, la diferencia puede generar confusión, así como errores en los cálculos y al resolver problemas.
Notarás que el radio y la apotema forman un triángulo junto con el lado del polígono. Del mismo modo se aprecia que en este caso el radio de la circunferencia circunscrita es a su vez, la hipotenusa del triángulo —y la apotema solo un cateto—, lo que hace más clara la diferencia de sus longitudes al ser siempre mayor la hipotenusa.
Por otra parte, el triángulo representa un elemento fundamental en la consideración de superficies.
Cuando no se puede calcular de manera inmediata el área de un polígono, se intenta calcularla por partes triangulando el mismo. Y para comprobarlo, observa el siguiente video.
- Triangulaciones simples de los polígonos convexos
El planteamiento de un problema sobre el Teorema de Pitágoras no se refiere a los conceptos básicos de perpendicularidad, segmento o clasificación de los triángulos, porque está tratando de consolidar un nuevo aprendizaje.
La idea es que cada vez que aparezcan en el contexto de un problema o situación, puedes repasar mental o explícitamente las propiedades de los conceptos fundamentales de geometría.
Así, sus estructuras cognitivas del pensamiento se consolidarán de manera que sean verdades sobre las que se construya eficientemente cada nuevo aprendizaje de geometría en particular y de matemáticas en general.
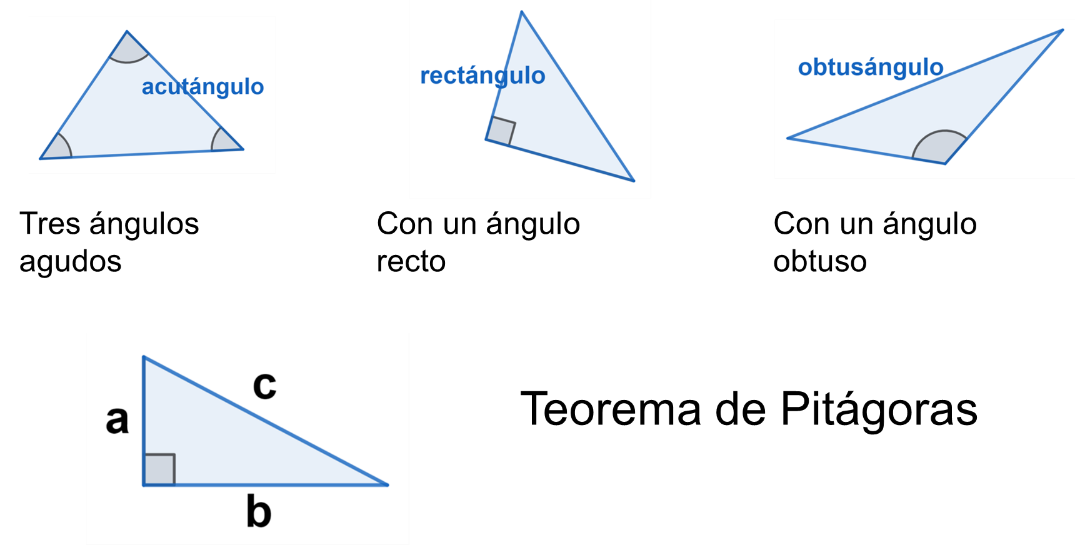
Se revisa ahora la clasificación de los triángulos por la medida de sus ángulos. En ella, los segmentos perpendiculares vuelven a ser un factor importante.
Si el triángulo tiene un ángulo recto es un triángulo rectángulo, si sólo tiene ángulos agudos, es un triángulo acutángulo. Y si tiene un ángulo obtuso es un triángulo obtusángulo.
Advertir que un triángulo es rectángulo trae consigo propiedades útiles al resolver situaciones. Una de ellas es el Teorema de Pitágoras.
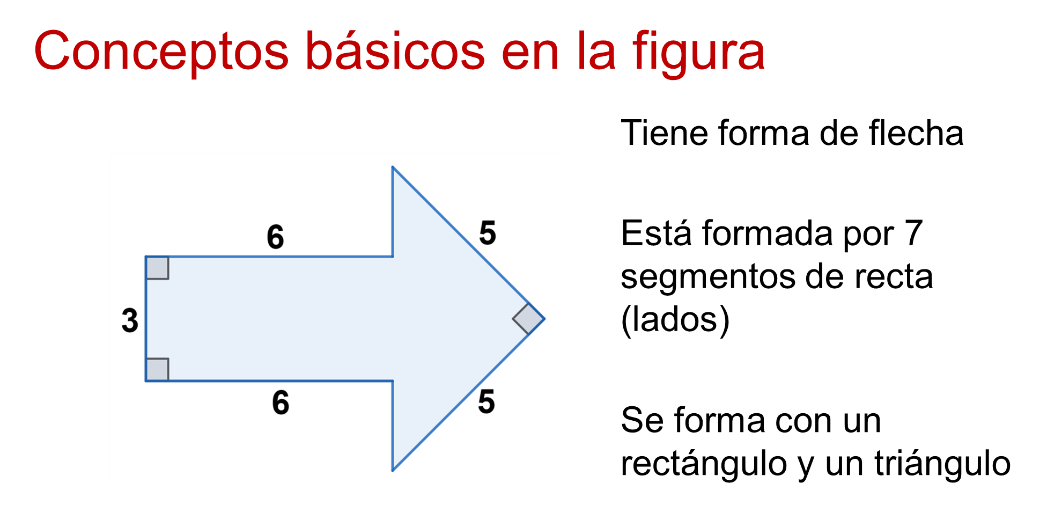
En las siguientes descripciones, se destaca la vinculación de conceptos geométricos fundamentales por medio del análisis de una figura geométrica en los distintos momentos de la educación básica.
Al presentar la figura, la situación permite incorporar los conceptos básicos según el grado de análisis que se requiera.
A modo de introducción, se puede cuestionar:
¿A qué objeto se asemeja la figura? A una flecha
¿Por cuántos segmentos de recta está formada? Por 7 segmentos
¿Cuáles son las dos figuras básicas que forman la figura? Un rectángulo y un triángulo.
Como puedes observar, son todos elementos reconocibles. Este tipo de situaciones estimulan el uso y la consolidación de los conceptos.
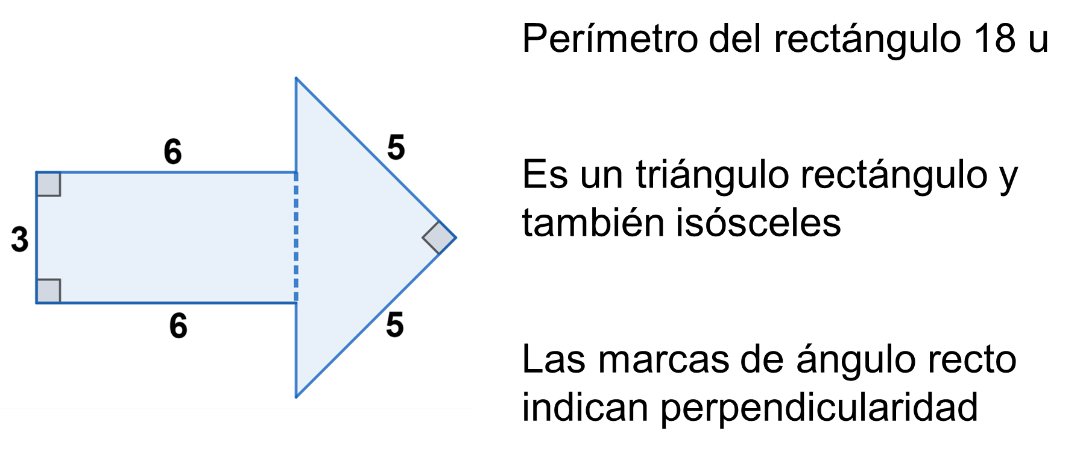
Analizando más elementos sobre la figura anterior, se tiene.
¿Cuál es el perímetro del rectángulo? 18 unidades.
¿De qué tipo es el triángulo? Es un triángulo isósceles por la medida de sus lados. Y es un triángulo rectángulo por la marca de ángulo recto que aparece entre dos de sus lados.
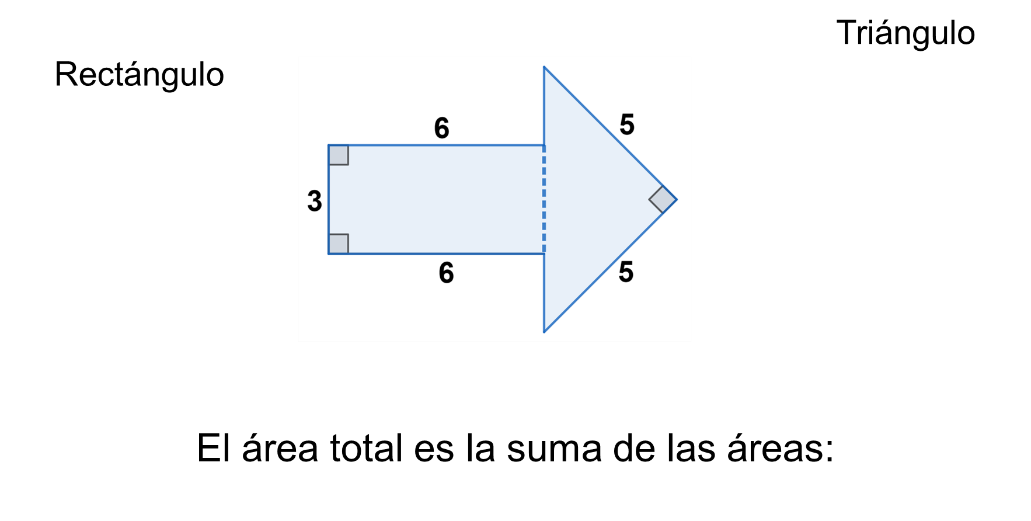
Con esta información, ya se puede determinar el área de la figura. Para ello se considera la suma del área del rectángulo y la del triángulo.
En el caso del triángulo, el concepto de altura, asociado al de perpendicularidad, permite saber que como dos de sus lados son perpendiculares, uno puede tomarse como base y el otro, como altura para usar la fórmula correspondiente.
Cada triángulo tiene tres bases y tres alturas; el segmento que representa a la altura no siempre queda al interior del triángulo.
Al calcular y sumar las áreas, el área total es de 30.5 unidades cuadradas.
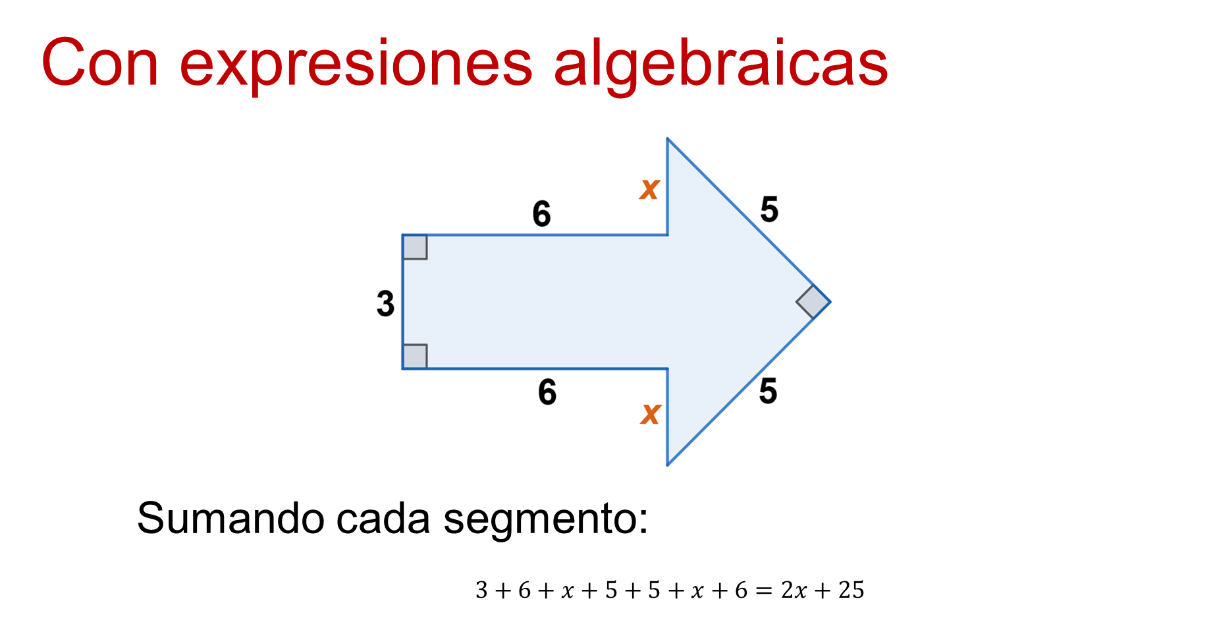
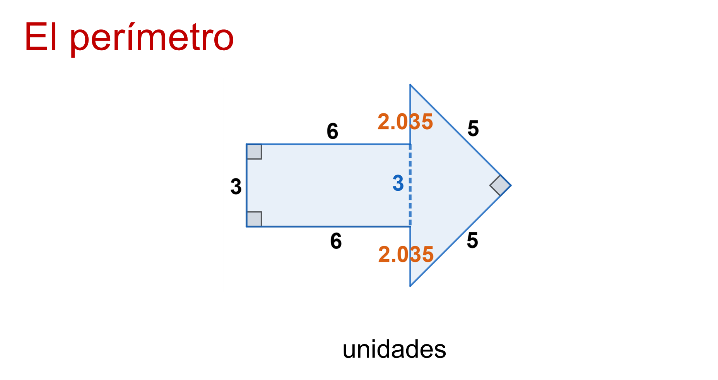
¿Qué tal si se asocia con expresiones algebraicas? Agregando “x” a cada segmento que no tiene medida, se solicita la expresión algebraica del perímetro de la figura.
Entendiendo el perímetro como la suma de los segmentos, que son los lados del polígono, 3 más 6 más “x”, más 5, más 5, más “x”, más 6, es igual a 2 “x” más 25.
Has repasado todos los conceptos básicos involucrados en la solución; eso te da significación, pues es la suma de las pequeñas partes la que lleva a la solución correcta de cada situación.
La clasificación de triángulos y ángulos atribuye nuevos nombres y propiedades válidas y útiles para las consideraciones geométricas.
Por ello, se pide “Determinar el perímetro de la figura geométrica”.
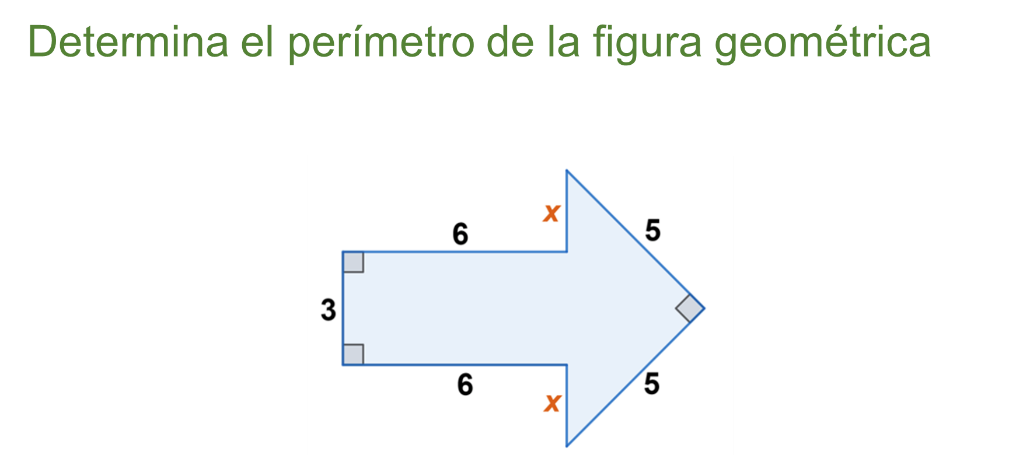
Recordando que el perímetro de un polígono se determina sumando todos sus lados, el problema se reduce a encontrar la medida de los segmentos que no muestran su dimensión y que se han representado con “x”.
Los segmentos son parte del lado mayor del triángulo rectángulo, la hipotenusa.
En un primer paso, se utiliza la expresión algebraica del Teorema de Pitágoras para saber la medida de la hipotenusa. Luego se resta la medida del lado de 3 unidades del rectángulo, con lo que se conoce la medida de los segmentos faltantes, y así sumar los lados de la figura.
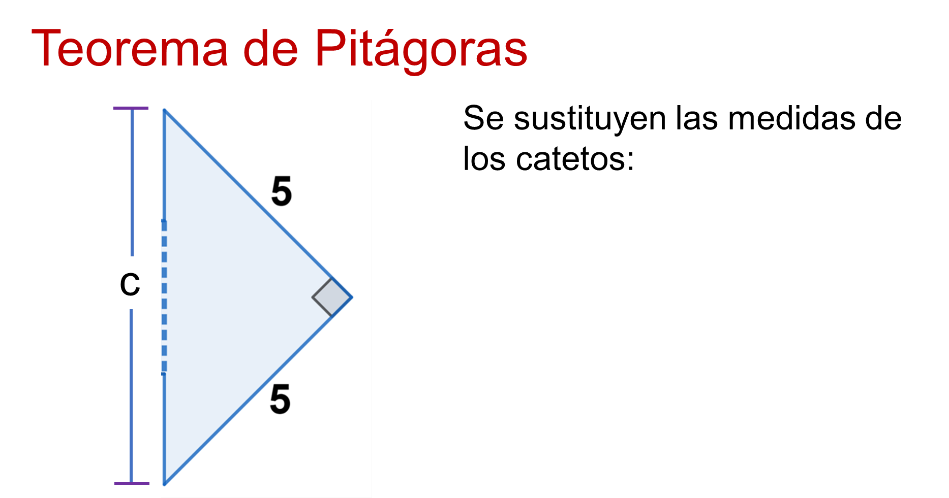
Los catetos del triángulo miden 5 unidades cada uno.
Se sustituye en la expresión algebraica del Teorema de Pitágoras “a” cuadrada más “b” cuadrada, igual a “c” cuadrada.
Entonces, 5 al cuadrado más 5 al cuadrado es igual a “c” cuadrada. “C” al cuadrado es igual a 50, por lo que el valor de “c” es igual a la raíz cuadrada de 50, aproximadamente a 7.07.
Al restar el lado de 3 unidades del rectángulo queda 4.07. Al dividir entre dos, cada uno de los segmentos que se buscan mide 2.035. El perímetro es 29.07 unidades.
Cómo pudiste observar, el reto consiste en recordar todos los elementos básicos aprendidos en su paso por la educación básica.
Para lograr esto, la asimilación de los conceptos fundamentales debe ser gradual. No se trata de memorizar definiciones, sino de comprender los conceptos, su interrelación y su utilidad inmediata y potencial al resolver situaciones matemáticas.
No es algo que ocurra de manera inmediata. Los conceptos fundamentales aparecen con frecuencia en diversos desafíos mientras se aprende geometría, y la mayoría de las veces, como el medio para un fin.
Sigue vinculando conceptos. La distancia entre un punto y una recta o segmento se obtiene trazando un segmento perpendicular a la recta hasta el punto. Perpendicularidad, segmento y distancia son conceptos de frecuente aparición en la “simetría axial”.

La simetría axial establece que dos puntos son simétricos respecto a una recta o eje, si estando en lados opuestos de la recta se encuentran a la misma distancia de esta.
Y si se trata de un polígono, la condición aplica para cada uno de los puntos que son vértices.
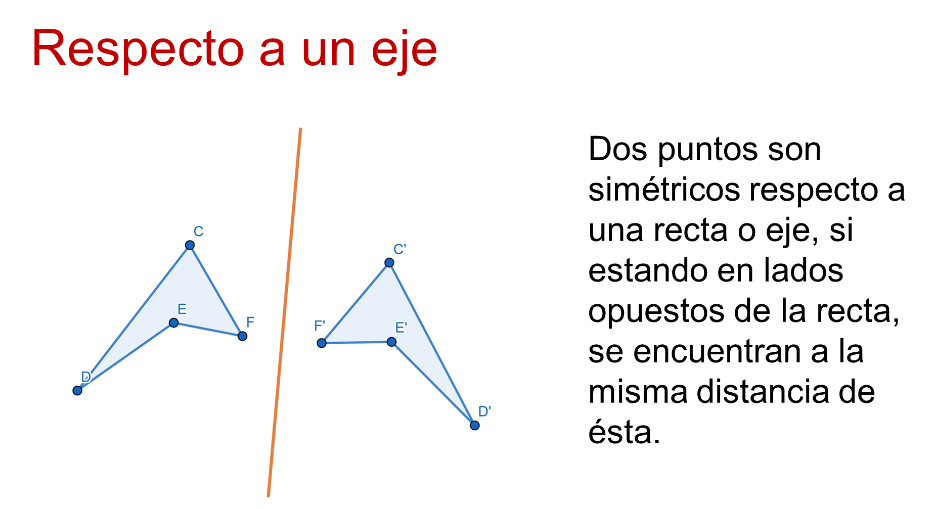
Sin importar el número de vértices que tenga el polígono, los fundamentos son los mismos.
Se traza una recta perpendicular al eje que pase por el primer punto. Para determinar distancias iguales a ambos lados del eje, se usa la regla o en este caso, una circunferencia. El punto donde se intersecan la perpendicular y la circunferencia es el simétrico del primer punto.
Después, para el siguiente vértice del polígono, se repite el procedimiento. Se traza una perpendicular al eje de simetría que pase por el segundo punto seleccionado. Con centro en el punto de intersección de esa recta y el eje, se construye la circunferencia para determinar distancias iguales. El punto de intersección es el simétrico del segundo punto del polígono.
Para el tercer vértice, se repite el procedimiento. Una vez obtenidos todos los vértices del polígono, se trazan los segmentos correspondientes para obtener el simétrico del polígono dado.
En consecuencia, cada segmento que une dos puntos simétricos es perpendicular respecto al eje de simetría.
Como has podido notar, estos temas no dependen únicamente de los conceptos fundamentales como segmento de recta y perpendicularidad, pero se mantienen presentes las propiedades y la utilidad de estos conceptos al construir conceptos posteriores.
En los problemas de semejanza de triángulos, cuando un problema menciona la relación entre la altura de un árbol y una persona —aunque no se menciona de manera explícita—, se considera que tanto el árbol como la persona guardan perpendicularidad respecto al suelo.
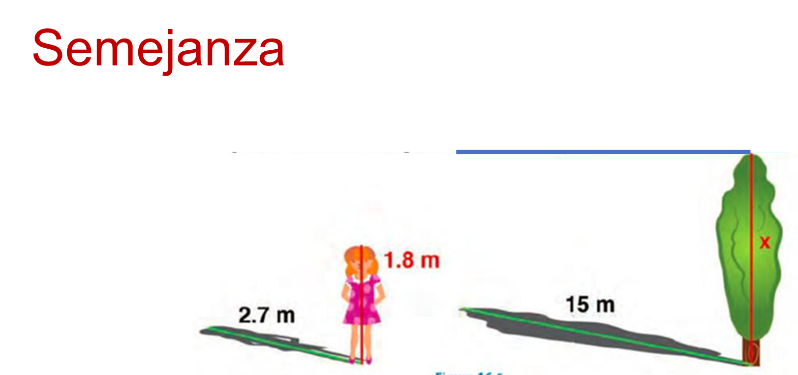
Eso justifica el uso de las propiedades de semejanza al plantear las expresiones para hallar la solución. Tener presentes los conceptos resulta un sólido comienzo en la búsqueda de la solución.
En situaciones que remiten al Teorema de Pitágoras, reconocer la perpendicularidad entre una pared y el suelo, así como las propiedades de las figuras básicas, son necesarios para resolver problemas.
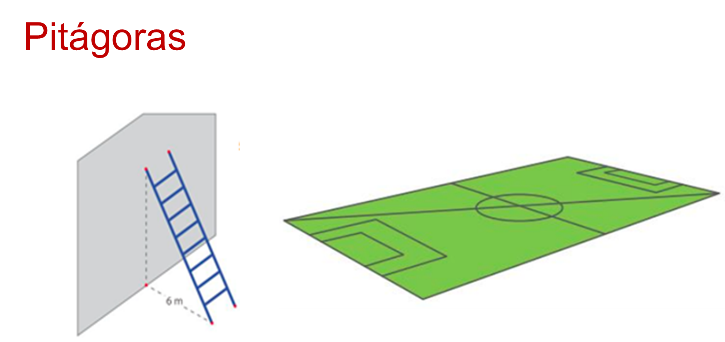
Como puedes observar a medida que se accede a los grados escolares superiores, los nuevos aprendizajes son más demandantes. No obstante, los conceptos fundamentales permanecen.
Es probable que estos conceptos como segmento de recta, paralelismo, clasificación de ángulos, paralelismo y perpendicularidad, y las posiciones relativas de las rectas, por mencionar algunos, se consideran para principiantes, porque son temas conocidos durante los primeros años escolares que soportan la carga de los aprendizajes geométricos posteriores, como en el estudio de la trigonometría y del plano cartesiano.
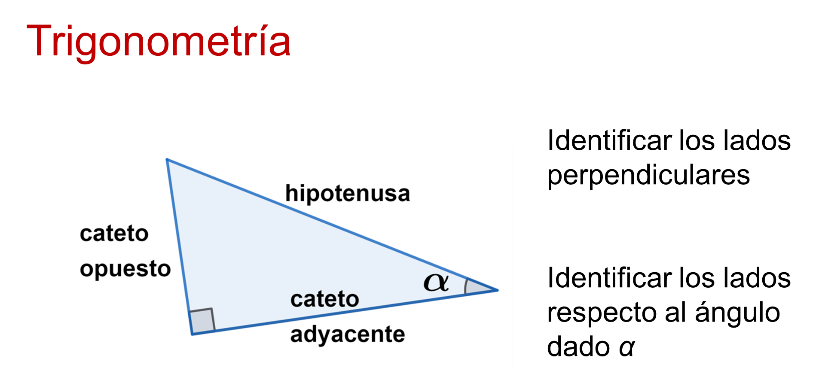
En el estudio de la trigonometría, identificar los lados perpendiculares del triángulo rectángulo es de suma importancia. La correcta caracterización del ángulo recto es determinante para denotar los segmentos que son cateto opuesto, cateto adyacente e hipotenusa.
El plano cartesiano y, en consecuencia, la localización de puntos y gráficas, toman como punto de partida la consideración de la perpendicularidad.
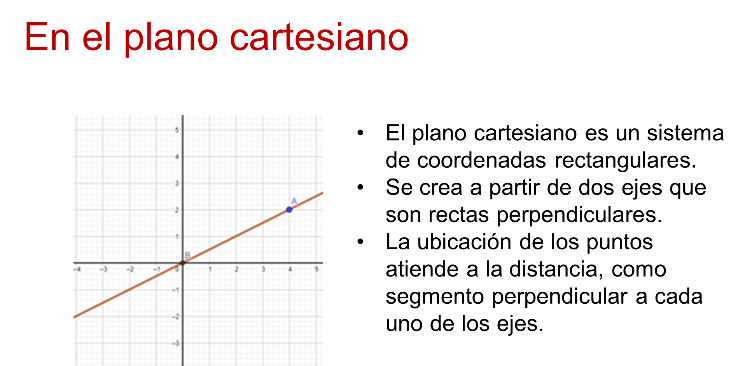
Se trata de un sistema de coordenadas rectangulares, cuya representación atiende las propiedades de las rectas y segmentos perpendiculares que se vinculan con expresiones algebraicas.
No se abordaron todos los conceptos fundamentales, pero se ha ejemplificado su influencia y su permanente aparición a lo largo del trayecto formativo de la educación básica.
Si en cada oportunidad, al abordar una situación de geometría se repara en esos conceptos básicos, se espera que cada nuevo aprendizaje se incorpore con solidez a la estructura del razonamiento deductivo que promueve la geometría.
Albañiles, topógrafos, arquitectos, diseñadores gráficos, controladores de tráfico aéreo, son personas profesionales utilizan de manera cotidiana conceptos geométricos fundamentales.
Algunos lo expresan mediante el lenguaje formal, otros por medio de programas de computadora, por medio de hilos o contando los pasos.
Cada uno de los conceptos geométricos que se adquieren desde la edad preescolar resulta una herramienta que suma eficiencia al enfrentar retos y situaciones tanto escolares como del entorno cotidiano.
El reto de hoy:
Siempre que te sea posible, comparte las anotaciones con tus compañeros y tu maestra o maestro. Socializar tus conjeturas resultará de gran utilidad para apropiarse de los conocimientos y aprendizajes esperados.
Busca en las páginas de los libros de texto que aún conserven información relacionada con los conceptos de geometría.
¡Buen trabajo!
Gracias por tu esfuerzo.
* Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.