La estadística
La estadística
Aprendizaje Esperado: consolida contenidos del eje: análisis de datos.
Énfasis: integrar contenidos del tema: estadística.
¿Qué vamos a aprender?
En esta sesión conocerás tu progreso con respecto a los aprendizajes esperados “Recolectar, registrar y leer datos en histogramas, polígonos de frecuencia y gráficos de línea” y “Usar e interpretar las medidas de tendencia central, el rango y la desviación media de un conjunto de datos y decidir cuál de ellas conviene más en el análisis de los datos en cuestión”.
Ten a la mano tu cuaderno o algunas hojas de papel, lápiz, goma, sacapuntas y bolígrafo para hacer tus anotaciones. Así como tu libro de texto. En caso de tener una discapacidad visual, prepara hojas leyer, un punzón y una regleta.
¿Qué vamos a hacer?
Para iniciar esta sesión, considera la siguiente tabla y cópiala en tu cuaderno.
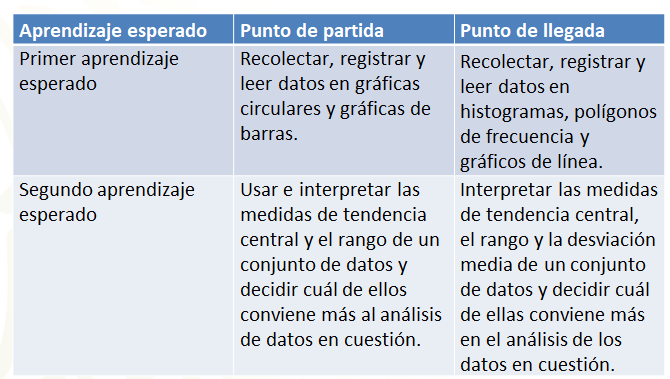
En la primera columna puedes distinguir que en este grado escolar se pretende alcanzar dos aprendizajes dentro del estudio de la Estadística.
En la segunda columna, se indica el punto del que puedes partir para lograr cada aprendizaje esperado de segundo grado. Estos son aprendizajes que tú has construido desde tu educación primaria.
Específicamente, se considera como punto de partida del primer aprendizaje esperado, “recolectar, registrar y leer datos en gráficas circulares y gráficas de barras”.
Como punto de partida del segundo aprendizaje esperado, se considera usar e interpretar las medidas de tendencia central y el rango de un conjunto de datos y decidir cuál de ellos conviene más al análisis de datos en cuestión.
En la tercera columna, se indican los aprendizajes esperados a los que se espera llegar con el estudio de las matemáticas en segundo de secundaria. El primero de ellos, consiste en recolectar, registrar y leer datos en histogramas, polígonos de frecuencia y gráficos de línea.
El segundo, consiste en interpretar las medidas de tendencia central, el rango y la desviación media de un conjunto de datos y decidir cuál de ellas conviene más en el análisis de los datos en cuestión.
A continuación, revisarás problemas y preguntas de reflexión para que conozcas tu progreso en cada aprendizaje esperado.
Se considera como punto de partida usar e interpretar las medidas de tendencia central y el rango de un conjunto de datos y decidir cuál de ellos conviene más al análisis de datos en cuestión.
Para verificar que cumplen con los conocimientos previos del tema, realiza el siguiente juego.
¿Alguna vez has jugado a los volados?
Los volados consisten en lanzar una moneda al aire y adivinar si caerá águila o sol.
Díaz y Batanero propusieron a sus estudiantes un experimento con volados.
El experimento, consistió en inventar los resultados de una secuencia de 20 volados, de tal manera que nadie se diera cuenta que la secuencia es inventada.
Tú en casa, ¿qué tomarías en cuenta para inventar los resultados de 20 volados, de tal manera que nadie se dé cuenta que son inventados?
Los alumnos de Díaz y Batanero, sugirieron que el número de águilas y de soles, debe ser aproximadamente igual, ya que hay las mismas posibilidades para el águila que para el sol.
También, tú toma estas consideraciones en casa, anota en tu cuaderno una secuencia e intenta inventar los resultados, tomando en cuenta que, en la realidad, no siempre sale la misma cantidad de águilas que de soles.

Una secuencia inventada puede ser en la que se obtengan, por ejemplo, los siguientes resultados: águila, sol, águila, águila, sol, sol, águila, sol, águila, sol, sol, águila, sol, sol, sol, sol, águila, águila, sol, águila.
En total, hay 11 soles y 9 águilas. Por lo tanto, cumple con las consideraciones que se habían establecido, el número de caras y de cruces debe ser aproximadamente igual.
Tú, en casa, inventa tu propia secuencia de 20 volados. Recuerda que nadie debe darse cuenta de que es inventada. Otras personas deben pensar que la moneda se ha lanzado en realidad.
Ahora bien, tú, en casa, ¿qué harías para averiguar si los alumnos de Batanero y Díaz, lograron inventar secuencias de 20 volados, sin que nadie se diera cuenta de que fueron inventadas?
Para averiguarlo, Díaz y Batanero pidieron a cada alumno que, además de inventar una secuencia de volados, lanzarán realmente la moneda 20 veces y anotaran la secuencia real.
Una secuencia real pudo ser la siguiente: sol, sol, águila, sol, sol, sol, águila, sol, águila, sol, sol, águila, sol, sol, sol, sol, águila, águila, sol, sol. En este caso, salieron 14 soles y 6 águilas.
Luego, propusieron comparar el número de soles de la secuencia real y de la inventada. En el ejemplo, en la secuencia inventada salieron 9 soles y en la real, 14 soles.

Posteriormente, propusieron comparar el número de soles de la secuencia real y de la inventada, pero de todos los alumnos de la clase.
¿Qué harías en casa para realizar la comparación entre las secuencias reales y las inventadas de todos los alumnos de la clase
Un primer paso, podría consistir en recolectar datos. En este caso los datos son el número de soles de las secuencias inventadas y reales de todos los alumnos.
En el caso de los alumnos de Díaz y Batanero, el número de soles de las secuencias inventadas por sus 27 alumnos fue la siguiente:
| 10, 12, 11,10, 11, 9, 10, 11, 9, 10, 10, 10, 7, 10, 10, 10, 10, 12, 11, 10, 9, 10, 10, 9, 10, 12, 11. |
En cambio, el número de soles de las secuencias reales fue la siguiente:
| 11, 11, 11, 8, 7, 8, 9, 11, 10, 9, 9, 9, 9, 14, 7, 10, 9, 10, 11, 13, 11, 8, 8, 11, 12, 9, 8. |
Con lo anterior, ¿cómo harías para distinguir una secuencia real de volados de una secuencia inventada?

Para contestar la pregunta que plantea Benjamín, puedes organizar en gráficas los datos de las secuencias reales y de las inventadas. Para eso en el eje horizontal se coloca la variable “número de soles” y en el eje vertical la cantidad de secuencias en las que se obtuvo ese número de soles.
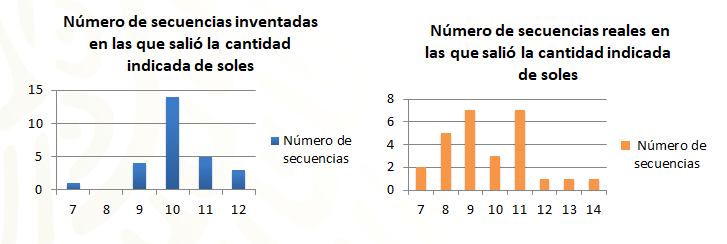
Compara las gráficas. ¿Cuál es el dato que aparece con mayor frecuencia en las secuencias inventadas? ¿Y en las secuencias reales?
Observa que, en la gráfica de las secuencias inventadas, el dato que aparece con mayor frecuencia es el 10, mientras que en el de las secuencias reales, son el 9 y el 11. ¿Cómo interpretarías esto?
Fíjate que en la gráfica de las secuencias inventadas el dato que más se repite es el 10, porque los alumnos de Díaz y Batanero consideraron que hay las mismas posibilidades de caer águila que de caer sol. En la realidad, los datos se aproximan a ese valor, pero no tan exactamente como supusieron los alumnos de Díaz y Batanero.
También puedes resumir todos los datos calculando la media de las secuencias inventadas y la de las secuencias reales. Para calcular la media, recuerda que debes sumar todos los datos y dividir el resultado entre el número total de datos.
Para las secuencias inventadas, se tiene que la media de volados en los que salió sol es de 10 más 12, más 11, más 10, más 11, más 9, más 10, más 11, más 9, más 10, más 10, más 10, más 7, más 10, más 10, más 10, más 10, más 12, más 11, más 10, más 9, más 10, más 10, más 9, más 10, más 12 más 11.
Luego, el resultado de la suma se divide entre 27. Al realizar la suma se obtiene 274 y al dividirla entre 27, se obtiene 10 punto 14 aproximadamente.

Al realizar un procedimiento similar para las secuencias reales, se obtiene que la media de volados en los que salió sol es de 9 punto 74. ¿Cómo interpretarías esos valores?
Para contestar la pregunta que plantea, considera que la media es el valor alrededor del cual se encuentran los datos. Tanto en la secuencia real como en la inventada, la cantidad de soles es aproximadamente 10. Como la cantidad de volados es 20, el que el valor de la media sea 10 quiere decir que, en la secuencia inventada, sí se tomó en cuenta que hay las mismas posibilidades de caer águila que de caer sol.
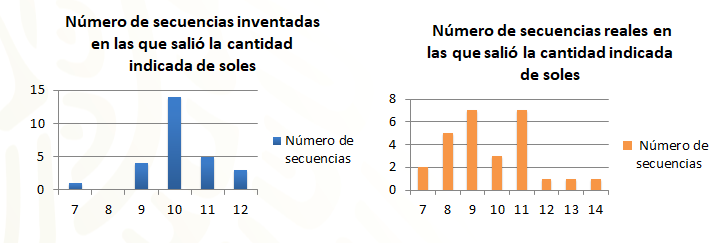
Si la media no proporciona información para distinguir entre la secuencia real y la secuencia inventada, ¿a qué otra medida puedes recurrir?
En las gráficas, puedes observar que en la secuencia inventada los datos corren de 7 a 12. Esto quiere decir que el rango es de 5, ya que el rango es la diferencia entre el dato de mayor valor menos el dato de menor valor. En cambio, en la secuencia real, los datos corren de 7 a 14. Es decir, el rango es de 7. ¿Qué significa esto?
Que en la realidad los datos varían más, de 7 a 14, de lo que cabría esperar, de 7 a 12.
Con el análisis anterior se concluye, ¿cómo podrías distinguir entre una secuencia de volados real y una secuencia inventada?
Para inventar secuencias de volados, las personas suelen tomar en cuenta que hay la misma posibilidad de caer águila que de caer sol. Por lo tanto, si se tiran 20 volados, en promedio las personas propondrán que el número de soles es cercano a 10. Esto es adecuado y ocurre en la realidad.
Lo que no suelen tomar en cuenta las personas es que en la realidad los valores suelen variar más. Las personas suelen proponer que en 20 volados la cantidad de soles siempre será muy cercana a 10, por ejemplo, de 7 a 12, pero en la realidad la cantidad de soles puede alejarse más de esos valores, por ejemplo, de 7 a 14.
Hasta aquí, se han utilizado gráficas de barras, la media y el rango para comparar conjuntos de datos. ¿Estás gráficas y medidas serán suficientes para comparar conjuntos de datos o se requieren otras?
Para contestar la pregunta que se ha planteado, se ha propuesto el siguiente problema.
Una profesora tiene dos grupos a los que les aplicó un examen distinto.
| Para el grupo 1 sus estudiantes obtuvieron las siguientes calificaciones: | Para el grupo 2 sus estudiantes obtuvieron las siguientes calificaciones: |
| 6 punto 6, 7 punto 1, 7 punto 1, 7 punto 2, 7 punto 2, 7 punto 6, 7 punto 6, 7 punto 6, 7 punto 6, 7 punto 7, 7 punto 7, 7 punto 7, 7 punto 8, 7 punto 8, 7 punto 9, 8 punto 1, 8 punto 1, 8 punto 1, 8 punto 1, 8 punto 1, 8 punto 2, 8 punto 2, 8 punto 2, 8 punto 2, 8 punto 3, 8 punto 3, 8 punto 3, 8 punto 3, 8 punto 4, 8 punto 4, 8 punto 4, 8 punto 4, 8 punto 6, 8 punto 6, 8 punto 7, 8 punto 7, 8 punto 7, 8 punto 8, 8 punto 8, 8 punto 8, 8 punto 9, 8 punto 9, 9 punto 1, 9 punto 2, |
6 punto 6, 6 punto 7, 7 punto 1, 7 punto 2, 7 punto 3, 7 punto 4, 7 punto 6, 7 punto 6, 7 punto 7, 7 punto 7, 7 punto 8, 7 punto 8, 8 punto 1, 8 punto 1, 8 punto 2, 8 punto 2, 8 punto 3, 8 punto 3, 8 punto 3, 8 punto 4, 8 punto 6, 8 punto 6, 8 punto 7, 8 punto 7, 8 punto 7, 8 punto 8, 8 punto 8, 8 punto 8, 8 punto 9, 8 punto 9, 9 punto 1, 9 punto 1, 9 punto 2, 9 punto 2, 9 punto 2, 9 punto 2, 9 punto 3, 9 punto 3, 9 punto 4, 9 punto 4, 9 punto 6, 9 punto 6, 9 punto 6, 9 punto 6, 9 punto 7, 9 punto 7, 9 punto 8, 9 punto 8, 9 punto 8, 9 punto 8, 9 punto 8, 9 punto 8. |
¿Qué se puede concluir de ambos exámenes?
Analiza las diferencias entre los datos de este problema y los datos del problema de los volados.
Observa que, en el problema de los volados, los datos resultaron de un conteo y se expresaron con números naturales. Es decir, las cantidades son discretas. En cambio, en este problema los datos resultan de un proceso de medición y los números naturales no son suficientes. Es decir, las cantidades son continuas.
Ahora bien, en las gráficas de barras, las barras se encuentran separadas porque la variable que se estudia no puede tomar ciertos valores, como en el caso de los volados. Ahí no tendría sentido graficar 7 punto 5 soles o 7 punto 1 águilas.
En cambio, en el problema de las calificaciones, si tiene sentido graficar una calificación de 7 punto 3, por ejemplo. Entonces, se requiere otro tipo de gráficas, llamadas histogramas.
Así es, para construir histogramas primero se pueden organizar ambos conjuntos de datos, de menor a mayor. Luego, se puede organizar cada conjunto en intervalos. Por ejemplo, el primer intervalo puede ser de 6 punto 5 a 7 punto cero, sin tomar en cuenta al siete. El siguiente intervalo puede ser de 7 punto cero a 7 punto 5, sin considerar al 7 punto 5. El siguiente intervalo puede ser de 7 punto 5 a 8 punto cero, sin considerar al 8. El siguiente intervalo puede ir de 8 punto cero a 8 punto 5 sin considerar al 8 punto 5. Otro intervalo puede ir de 8 punto 5 a 9 punto cero, sin considerar al 9. Uno más de 9 punto cero a 9 punto 5 sin considerar al 9 punto 5. Y el último de 9 punto 5 a 10.
Luego, para cada grupo, en una tabla de frecuencias se puede registrar cuántos estudiantes obtuvieron la calificación que se encuentra en cada intervalo.
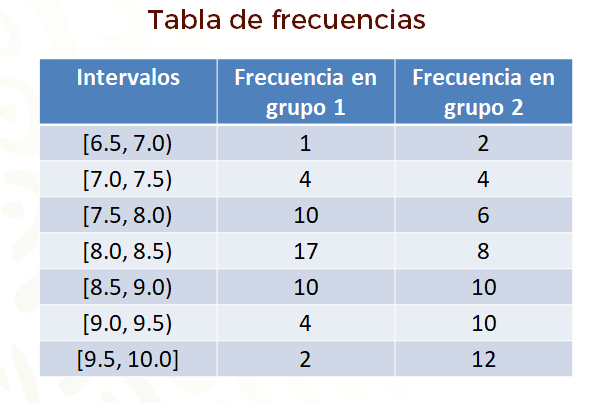
Para realizar los histogramas, en el eje horizontal se anotan los intervalos de la variable y en el eje vertical la frecuencia. Aquí las barras se colocan una al lado de la otra, indicando cada intervalo.
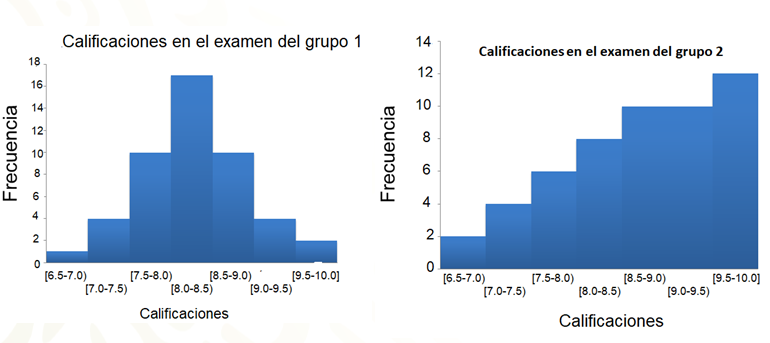
¿Qué información proporcionan los histogramas para diferenciar entre el examen aplicado al grupo 1 y el examen aplicado al grupo 2?
Se observa que en el grupo 1, la mayoría de los estudiantes obtuvo entre 7 punto 5 y 9 y pocos obtuvieron calificaciones muy bajas o muy altas. En cambio, en el grupo 2 la mayoría de los estudiantes obtuvo calificaciones altas y pocos obtuvieron calificaciones bajas.
Esto puede deberse a que el examen del grupo 2 fue demasiado fácil en comparación con el examen que se aplicó al grupo uno.
Con la resolución al problema se avanzó de utilizar gráficas de barras a interpretar histogramas.
Ahora, se avanzará de utilizar al rango como única medida de dispersión, a utilizar también la desviación media. Para eso, resuelve el siguiente problema.
En una competencia de carreras dos grupos de 10 jueces registran el tiempo que realizó un corredor.
| El grupo uno, anotó los siguientes tiempos en segundos. | En el grupo 2, anotó los siguientes tiempos en segundos. |
| 5 punto cero, 5 punto 4, 5 punto 4, 5 punto 2, 5 punto 4, 5 punto 1, 5 punto 3, 5 punto 2, 5 punto 2, 5 punto 4. | 5 punto 4, 5 punto cero, 5 punto 4, 5 punto cero, 5 punto cero, 5 punto 4, 5 punto cero, 5 punto cero, 5 punto 4, 5 punto 4. |
¿Cuál de los dos grupos de jueces piensas que utiliza instrumentos más precisos?
Uno de los criterios para determinar la precisión de los instrumentos es averiguar qué tan dispersos se encuentran los datos. Una medida para averiguar esto es el rango.
Al calcular el rango de los dos conjuntos se obtiene cero punto 4. De este modo el rango no es útil para decidir qué grupo de jueces utilizó el instrumento más preciso.
Esto se debe a que en el rango sólo se consideran los valores extremos de los conjuntos y no se toman en cuenta los valores interiores.
Puedes dibujar dos líneas y representar con puntos los datos de cada conjunto, como observarás a continuación:
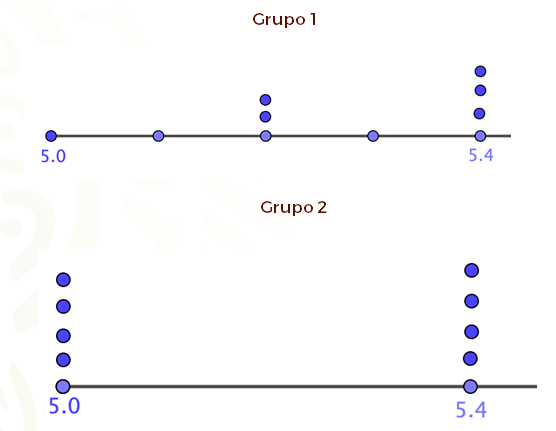
Observa que los datos del grupo 2 están más alejados que los del grupo 1. Para representar esto con un valor numérico, realiza lo siguiente con los datos del grupo 1.
Primero, calcula la media de cada conjunto. La media del primer conjunto es 5 punto 26, mientras que la media del segundo conjunto es 5 punto 2.
Luego calcula la distancia de cada dato a la media. Esta distancia es el valor absoluto de la diferencia entre los valores de la media y el dato. En la siguiente tabla se muestran las distancias para los datos del grupo 1.
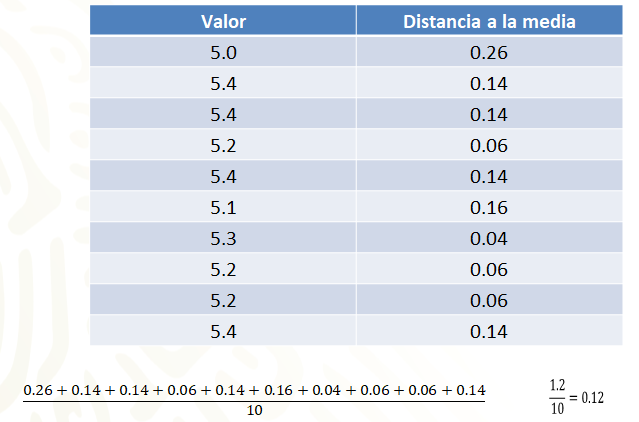
Posteriormente, se calcula el promedio de esas distancias. Al plantear las operaciones se obtiene que 0.26 más 0.14 más 0.14, más 0.06, más 0.14, más 0.16, más 0.04, más 0.06, más 0.06, más 0.14, da como resultado 1.2, el cual se divide entre el número de datos que son 10, es decir, 1.2 entre 10 da igual a 0.12. A este resultado se le conoce como desviación media.
Ahora hay que determinar la desviación media del grupo 2. La media de este grupo es 5 punto 2.
Calcula la distancia de cada dato a la media. Como se observa en la siguiente tabla, todas las distancias de los valores a la media es el mismo, cero punto 2.
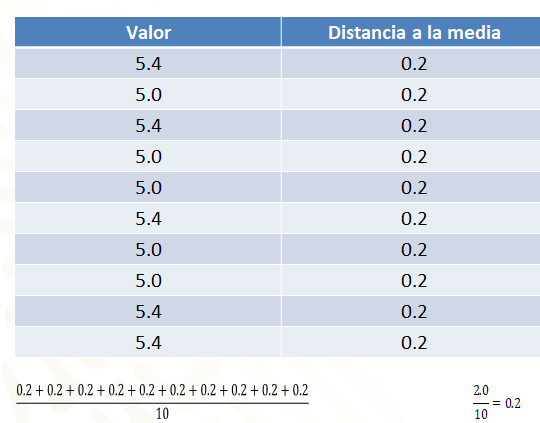
Posteriormente, se calcula el promedio de esas distancias. Para eso, se suman todas las distancias o se multiplica cero punto 2 por 10, de lo que se obtiene 2 punto cero. Al dividir este resultado entre 10, se obtiene cero punto 2.
En resumen, la desviación media de los tiempos registrados por el grupo 1 de jueces es de cero punto 12, mientras que la desviación media de los tiempos registrados por el grupo 2 de jueces es de cero punto 2.
En casa, contesta la siguiente pregunta: ¿para qué grupo de jueces la desviación media es mayor?
La respuesta es que como cero punto 2 es mayor que cero punto 12, se puede afirmar que los datos del grupo 2 de jueces tienen una mayor desviación media que los del grupo 1.
Pero, ¿qué significa que los datos del grupo 2 tengan una mayor desviación media que los del grupo 1?
La desviación media mide qué tan dispersos se encuentran los datos. Si los datos estuvieran totalmente unidos y se calculara la media, ¿qué valor se obtendría?
Por ejemplo, si se tiene un grupo, en donde los 10 jueces registran un tiempo de 5 segundos, ¿cuál sería la desviación media?
Primero, se calcula la media del conjunto. La media del conjunto es 5 segundos.
Luego, se calcula la distancia de cada dato a la media. Para cada dato, la distancia de ese dato a la media es cero.
Posteriormente, se calcula el promedio de las distancias de cada dato a su media. Para eso se suman las distancias de cada dato a su media y se divide entre el total de datos. Al plantear las operaciones se obtiene cero, más cero, más cero, más cero, más cero, más cero, más cero, más cero, más cero, más cero; entre 10. Al realizar la suma se obtiene cero. Al dividir este resultado entre 10, se obtiene cero.
Entonces, cuando los datos son iguales la desviación media es cero y entre más dispersos se encuentren los datos, el valor de la desviación media aumenta.
En el caso del problema de los jueces y el corredor, los tiempos registrados por los jueces del grupo 1 tienen una menor desviación media que los tiempos registrados por el grupo 2 y, por tanto, se puede plantear la hipótesis de que el instrumento que utilizó el grupo 1 de jueces es más preciso.
El reto de hoy:
En casa puedes regresar a la tabla de evaluación inicial y reflexionar sobre lo que aprendiste con respecto a los aprendizajes esperados, “Recolectar, registrar y leer datos en histogramas, polígonos de frecuencia y gráficos de línea”, y “Usar e interpretar las medidas de tendencia central, el rango y la desviación media de un conjunto de datos y decidir cuál de ellas conviene más en el análisis de los datos en cuestión”.
Asimismo, concluye los ejercicios que se realizaron en el desarrollo de la sesión, en caso de que te hayan quedado pendientes.
¡Buen trabajo!
Gracias por tu esfuerzo.
* Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas