Magnitudes y medidas
Magnitudes y medidas
Aprendizaje esperado: consolida contenidos del eje: forma, espacio y medida.
Énfasis: integrar contenidos del tema: magnitudes y medidas.
¿Qué vamos a aprender?
El objetivo de la sesión es consolidar contenidos del eje: forma, espacio y medida, con el propósito de integrar contenidos del tema: magnitudes y medidas
¿Qué hacemos?
Para iniciar, rescata algunos de los conceptos prioritarios del tema, para ello, resuelve un crucigrama.

Lee las descripciones y procura ir registrando las respuestas en tu libreta para que posteriormente cotejes los resultados.

Horizontal:
El número 1. es pulgada.
El número 7, kilómetro.
El número 9, magnitud.
El número 10, Kelvin.
El número 12, instrumentos de medida, abreviado corresponde.
El número 13, el metro.
El número 15, Sistema Inglés.
El número 17, kilogramo.
El número 19, tonelada.
El número 20, milla.
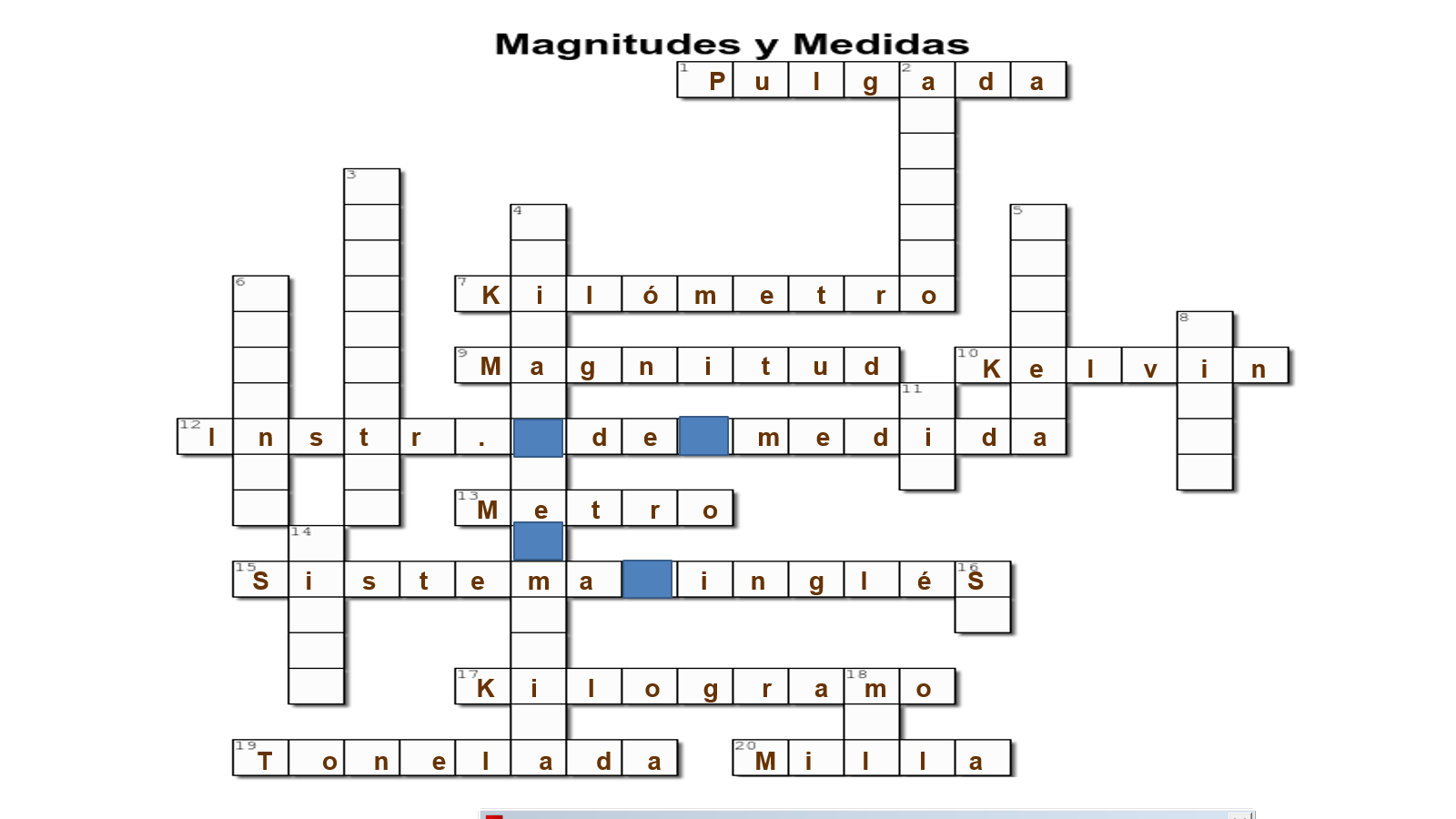
¿Contestaste de forma correcta todos los cuestionamientos?
Ahora, continua con las que van de manera vertical. Éstas pueden ser más sencillas debido a que ya tienes algunas letras.
El número 2, amperio.
El número 3, centímetro.
El número 4, unidad de medida.
El número 5, candela.
El número 6. segundo.
El número 8, libra.
El número 11, pie.
El número 14, litro.
El número 16, se refiere al Sistema Internacional de Unidades y se abrevia como “SI”.
El número 18, esta unidad es común en Ciencias y se llama mol.
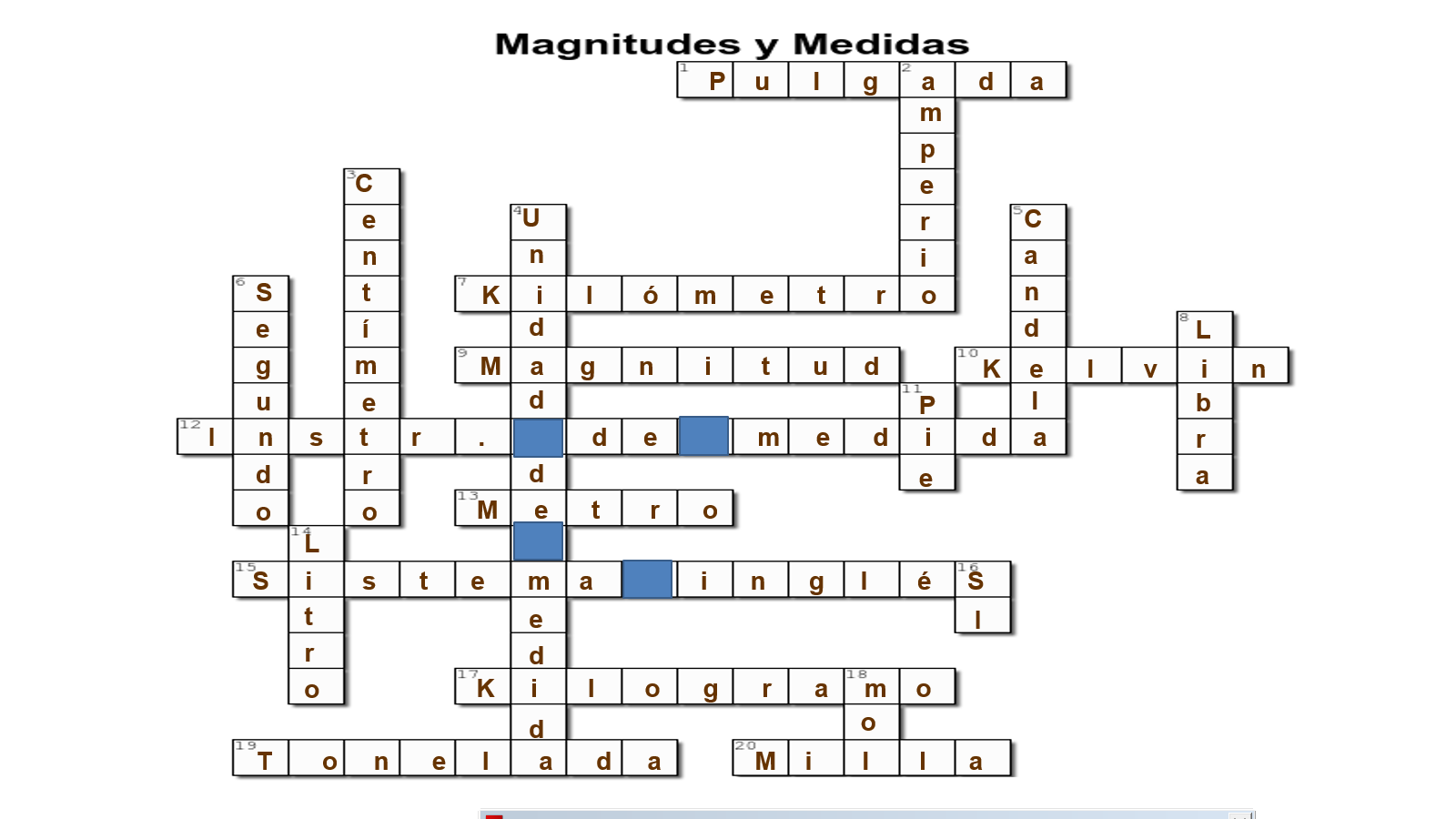
¿Cómo te fue?, ¿cuántos aciertos tuviste? Esperamos que tus respuestas hayan estado correctas, en caso de haber fallado en algunas, toma nota para que no se te olvide.
Para seguir reforzando tus conocimientos, continua con algunas situaciones de aplicación. Resolverás situaciones donde usarás algunas de las unidades de medida que has recordado.
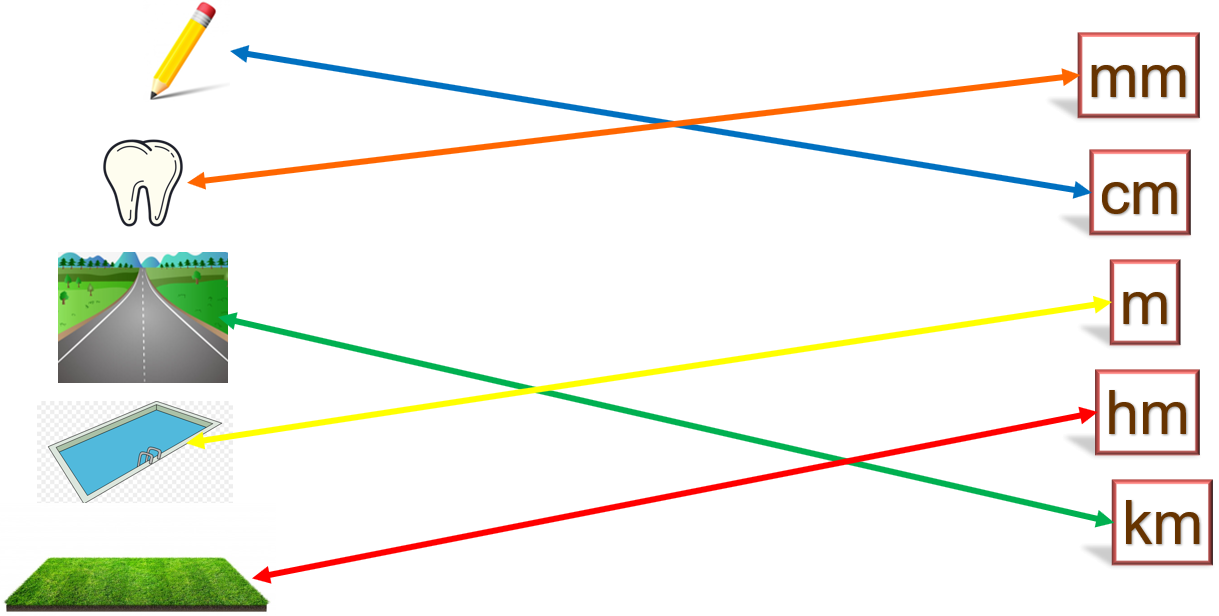
A continuación, se muestran algunas imágenes de objetos, relaciona con la unidad de medida que sería conveniente estimar su longitud.

El primer objeto es un lápiz y es conveniente medir su longitud en alguna unidad pequeña, entonces lo relacionamos con centímetros.
El siguiente objeto es una muela., como es más pequeña que el lápiz conviene medirla en milímetros entonces la relacionamos con mm.
La siguiente imagen corresponde a un tramo de camino carretero, como es una longitud más grande es conveniente medir en kilómetros, así que relacionamos con km.
El siguiente objeto es una piscina, para medir su longitud es conveniente usar los metros.
Por último, un terreno conviene medirlo en la última opción que tenemos y es hectómetros, es decir, 100 veces el valor del metro, entonces relacionamos con el símbolo hm.
Ahora vas a resolver una situación usando estas unidades de medida.
Ana tiene que recorrer 12 kilómetros dando vueltas a la pista de atletismo. El carril que recorre mide 400 metros. Si lleva 10 vueltas, ¿cuántos metros le faltan por recorrer?
Una forma de resolver el problema es trabajando con las mismas unidades de medida, entonces retomando la información, 1 km equivale a 1 000 metros por lo que multiplicamos 12 por 1 000 y obtenemos 12 000, lo que significa que Ana tiene que recorrer 12 000 metros.
Ahora contamos con la información que ha dado 10 vueltas de 400 metros, entonces, realizamos una multiplicación de estos dos factores, para conocer cuántos metros ha recorrido y resultan 4 000.
Entonces solamente falta restar el total de metros a recorrer con los metros que recorrió, es decir, 12 000 – 4 000 de lo que se obtiene 8 000. Por lo tanto, a Ana le falta por recorrer 8 000 metros.
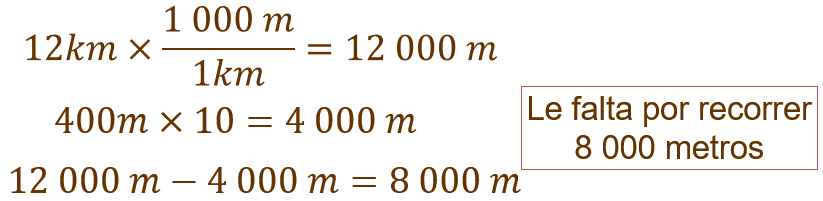
Analiza otra situación.
Luis elabora mascadas. Para cada una requiere de 42 centímetros de tela. Si tiene una tira de tela que mide 120 decímetros de largo, ¿cuántas mascadas puede elaborar?
Para resolver vas a trabajar con las mismas unidades de medida, para ello, considera que un decímetro es la décima parte del metro, lo que es igual a 10 centímetros; entonces, para convertir los decímetros a centímetros basta con multiplicar por 10. Es decir, 120 por 10, de lo que resulta 1 200 centímetros. Una vez que ya está todo con la misma unidad de medida, en este caso centímetros, se puede dividir el total de tela en centímetros entre la medida que se ocupa para cada mascada, quedando 1 200 entre 42, lo que es aproximadamente igual a 28.57. Esto significa que Luis puede elaborar 28 mascadas.

Analiza otra situación con unidades de longitud.
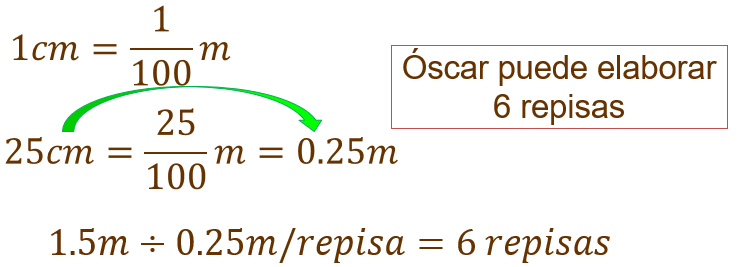
Óscar ha comprado un tablón de 1.50 metros de longitud para hacer repisas de 25 centímetros de largo. ¿Cuántas repisas puede elaborar?
Para dar solución a esta situación es recomendable trabajar con las mismas unidades de medida, en este caso vamos a trabajar con metros. Un centímetro es la centésima parte del metro, entonces 25 centímetros son 25 centésimos de metro, es decir, 0.25 metros. Ahora dividimos 1.5 entre 0.25 lo que da como resultado 6. Esto quiere decir que Óscar puede elaborar 6 repisas.
Manuel tiene que mover una cómoda de una habitación a otra, las medidas del mueble son 22 pulgadas de ancho por 30 pulgadas de largo y 85 pulgadas de altura; las medidas de la puerta por las cual pasará el mueble son de 2.75 pies de ancho por 7 pies de alto. ¿Podrá pasar la cómoda por la puerta?
En este caso vamos a trabajar con pulgadas, entonces, necesitamos conocer la equivalencia de pulgadas a pies y un pie equivale a 12 pulgadas. Así que, para conocer el valor de 2.75 pies, multiplicamos 2.75 por 12, de lo que se obtiene 33; lo que significa que la puerta mide 33 pulgadas de ancho.
Para calcular el alto de la puerta en pulgadas, realizamos el mismo procedimiento, entonces para conocer el valor de 7 pies se multiplica este valor por 12, obteniendo 84, lo que significa que la puerta tiene una altura de 84 pulgadas.
Para saber si puede pasar el mueble por la puerta vamos a realizar un cuadro comparativo con las medidas de la puerta y del mueble, en pulgadas.
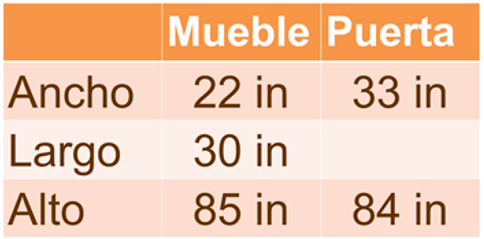
Observa que tanto el ancho como el largo del mueble si pueden pasar por la puerta, sin embargo, respecto a lo alto hay un problema ya que el mueble tiene 85 pulgadas de altura y la puerta 84. Así podríamos pensar que el mueble no pasa por la puerta, pero, ¿piensas que sí se podría resolver esto?, ¿Qué podría hacer Manuel para pasar ese mueble por la puerta?
Lo podría girar de forma que el largo y el ancho del mueble por sus dimensiones sí cabe en el ancho y la altura de la puerta.
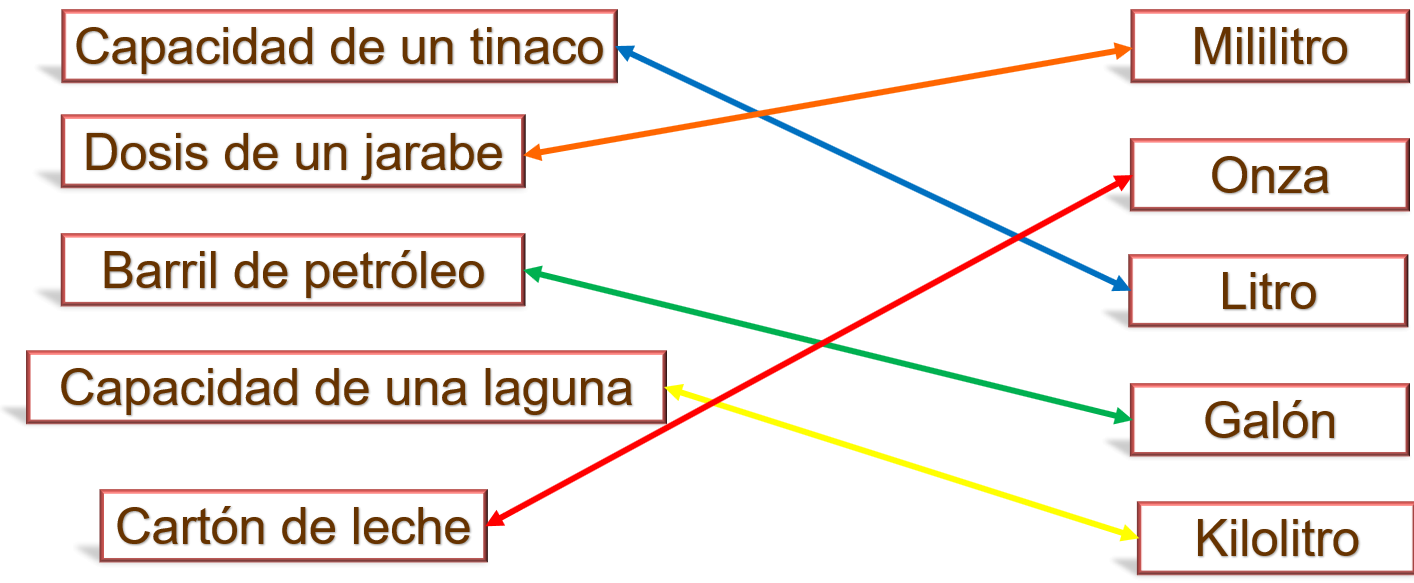
Ahora vas a relacionar cada situación con la unidad de medida que sería conveniente estimar su capacidad.

Iniciemos con el tinaco, éste es de uso común, así que seguramente ya sabes que su capacidad se presenta en litros.
Dosis de un jarabe, seguramente en alguna ocasión has visitado al médico y sus recetas las manejan en mililitros.
Ahora el barril de petróleo, probablemente has escuchado las noticias y cuando se refieren al barril de petróleo, el mismo barril puede ser referencia de capacidad, sin embargo, también usan el galón.
Para la capacidad de una laguna, en este caso si son cantidades más grandes, entonces se puede tomar como referencia el kilolitro, cabe mencionar que un kilolitro equivale a 1 000 litros.
Y por último el cartón de leche, su contenido se puede encontrar expresado tanto en litros como en onzas.
Ahora darás solución a otras situaciones.
Si un tinaco de agua se llena con 750 litros, ¿con cuántos hectolitros se llenan 8 tinacos iguales al anterior?
¿Cómo piensas que se resuelve?, ¿qué es lo primero que harías?
Primero convendría conocer con cuántos litros de agua se llenan los 8 tinacos, para ello, multiplicamos 750 por 8 lo que resulta 6 000 litros.
También sabemos que 100 litros equivalen a un hectolitro, entonces para dar respuesta, se divide 6 000 entre 100, de lo que se obtiene 60.
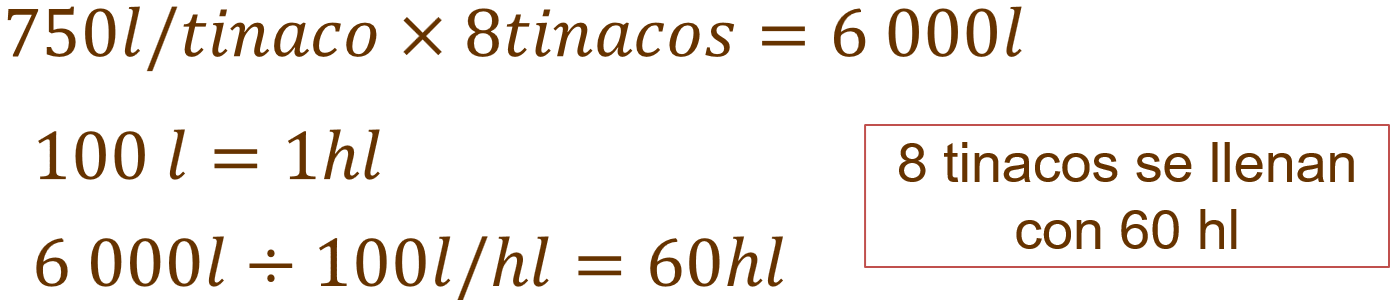
Esto quiere decir que, para llenar 8 tinacos con capacidad de 750 litros se requiere de 60 hectolitros.
Analiza otra situación.
El pediatra recetó a Dani 5 mililitros de un antibiótico cada 8 horas, durante 10 días. Cuando su papá fue a la farmacia encontró dos presentaciones del medicamento, uno con 120 mililitros y otra con 5.5 onzas, ¿qué presentación le conviene comprar?
Una manera de iniciar es saber cuántos mililitros va a tomar durante todo el tratamiento. Para ello, consideramos que un día tiene 24 horas, entonces se divide 24 entre 8, ya que son las horas que dejará pasar entre cada toma y el cociente es 3, es decir, que realiza 3 tomas diarias. Luego, si son 10 días, al multiplicar 3 por 10 obtenemos que, durante todo el tratamiento, realizará 30 tomas; luego multiplicamos 30 por 5 mililitros, resulta que el tratamiento de Dani consta de 150 mililitros de antibiótico.
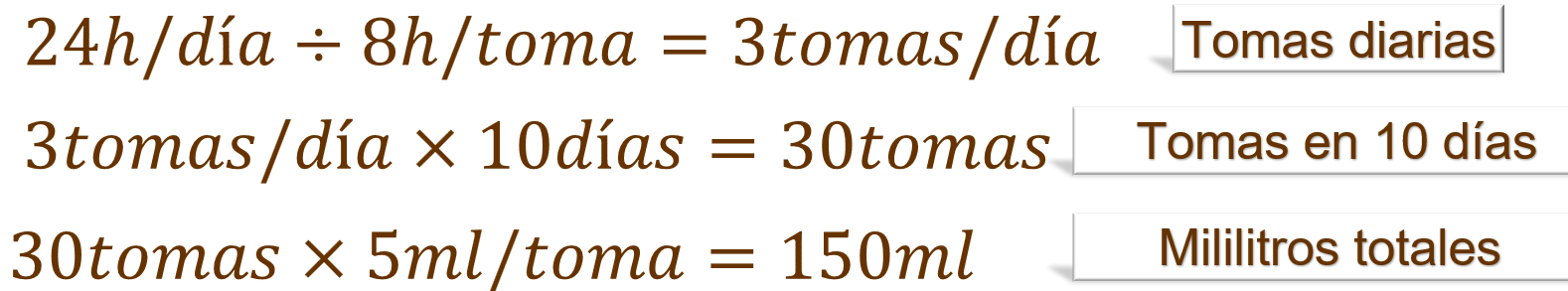
Con esto podemos decidir que la presentación de 120 mililitros no es muy conveniente, porque tendría que comprar dos de esa presentación.
Ahora, analiza la otra presentación.
Partimos de que una onza equivale a 29.57 mililitros, entonces, debemos determinar la equivalencia de 5.5 onzas en mililitros. Para esto, multiplicamos 5.5 por 29.57 de lo que resulta 162.635 mililitros.
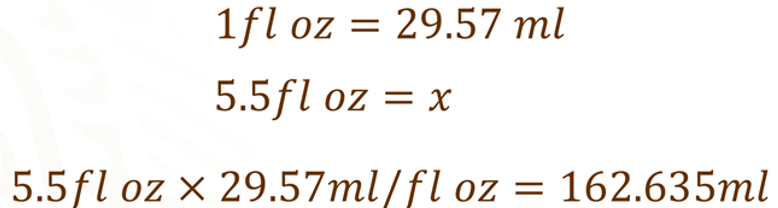
De esta manera podemos afirmar que esta presentación es la más conveniente que adquiera.
Realiza otra actividad; relaciona cada magnitud con la unidad que usarías para medirla.

Para la masa de una persona, la unidad de medida que se usa es el kilogramo.
Para la masa de un elefante se usan las toneladas.
Como la masa de una hoja es mínima se usan miligramos.
Para la bolsa de bombones se usan gramos.
Por último, el equipaje puede ser en libras.
Ahora, resuelve otra situación.
José tiene una masa corporal 42 kilogramos y su padre el doble que él. Un amigo que está de visita les dijo que su masa corporal es de 150 libras. ¿Cuál es la masa corporal de los tres juntos?
Como la mayoría de las masas corporales se encuentran en kilogramos, vamos a convertir la masa corporal del amigo en kilogramos. Una libra equivale a 0.45 kilogramos, entonces, para saber a cuántos kilogramos equivalen 150 libras, multiplicamos 150 por 0.45 y obtenemos 67.5 kilogramos. Ahora para conocer la masa corporal del papá, que es el doble de la de José, multiplicamos 42 kilogramos por 2, lo que es 84 kilogramos. A continuación, sumamos la masa corporal de los tres y obtenemos 193.5 kilogramos.
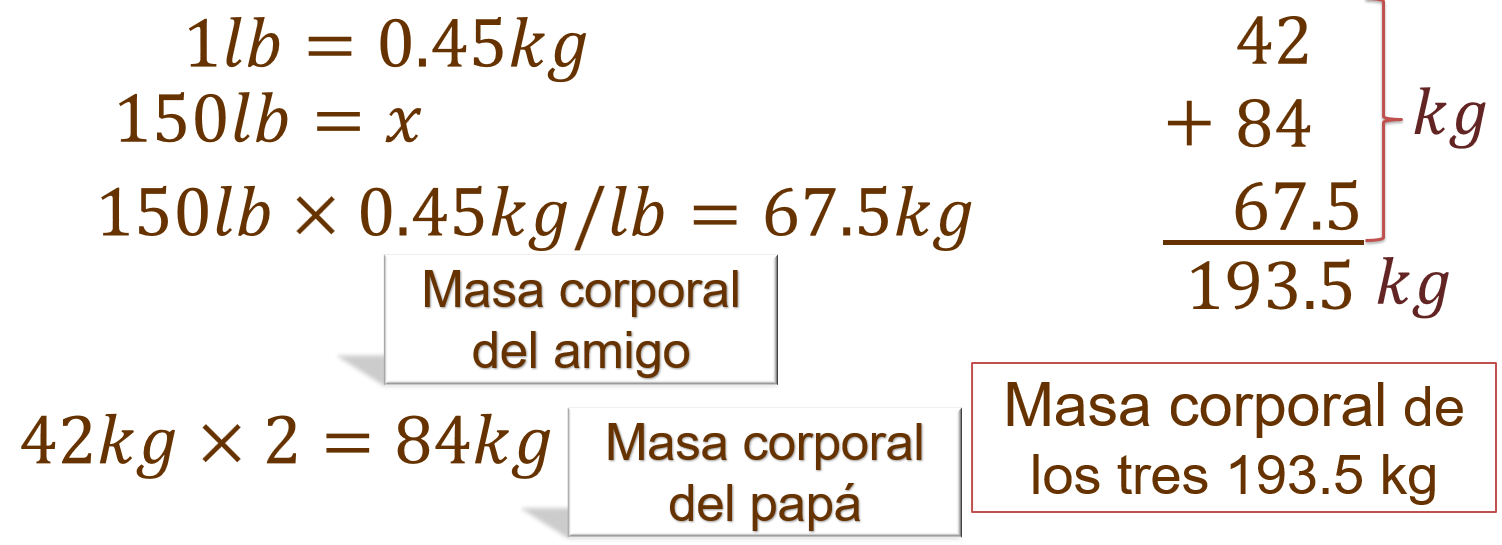
Y si las tres personas quieren subir a un ascensor que admite una carga máxima de 20 000 decagramos y quiere subir una persona más con 120 libras de masa corporal, ¿pueden subir al ascensor?
Para iniciar, 100 decagramos equivalen a un kilogramo, entonces, dividimos 20 000 entre 100, de lo que resulta 200. Esto significa que el elevador puede soportar hasta 200 kilogramos de carga. Ahora para conocer la equivalencia de 120 libras a kilogramos, se multiplica 120 por 0.45, lo que resulta 54 kilogramos. Ya habíamos calculado la masa corporal de las tres primeras personas, así que ahora solamente sumamos 193.5 kilogramos más 54 kilogramos y obtenemos 247.5 kilogramos.
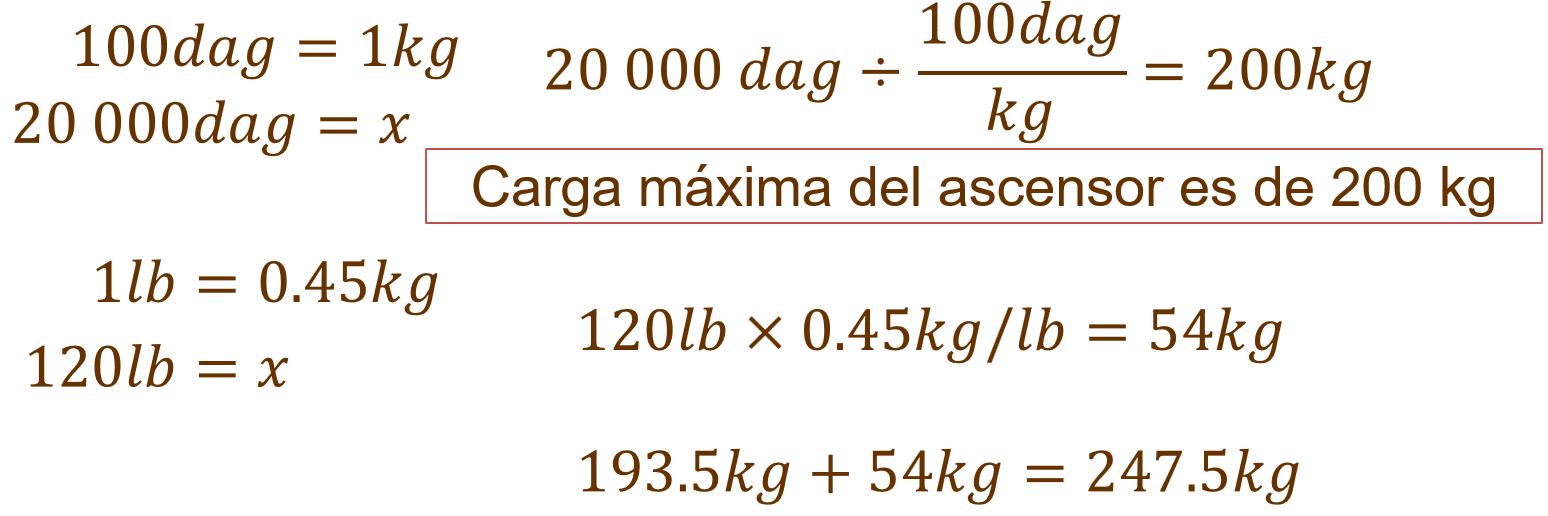
Observa que se excede de la carga máxima que soporta el elevador, así que podemos afirmar que no es posible que lo utilicen las 4 personas juntas.
Esperamos que lo trabajado te permita reforzar tus conocimientos sobre el tema Magnitudes y medidas.
Hay otras formas de resolver estas situaciones, aquí te compartimos una de ellas, pero puedes utilizar otras estrategias.
El reto de hoy:
Busca en tu libro de texto los temas relacionados y resuelve al menos dos situaciones de ellas. Luego comparte tus resultados con tu docente.
¡Buen trabajo!
Gracias por tu esfuerzo.
* Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas