Figuras y cuerpos geométricos
Figuras y cuerpos geométricos
Aprendizaje esperado: consolida contenidos del eje: forma, espacio y medida.
Énfasis: integrar contenidos del tema: figuras y cuerpos geométricos.
¿Qué vamos a aprender?
Esta sesión tiene como propósito integrar contenidos del tema: figuras y cuerpos geométricos.
¿Qué hacemos?
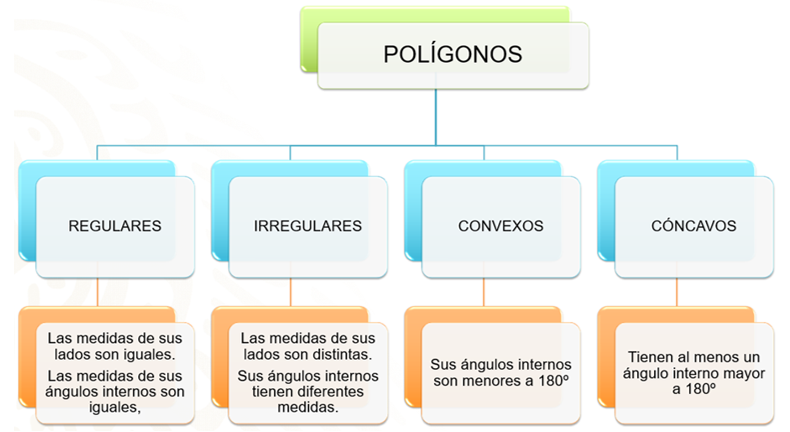
Iniciarás la sesión con la clasificación de los polígonos. Podemos distinguir polígonos regulares, irregulares, convexos y cóncavos. Los polígonos regulares son aquellos que tienen sus lados con las mismas medidas y cuyos ángulos internos también miden lo mismo, mientras que los polígonos irregulares no cumplen con estas características.
Por otro lado, los polígonos convexos se caracterizan porque sus ángulos internos son menores de 180 grados, mientras que los polígonos cóncavos se distinguen porque al menos uno de sus ángulos internos mide más de 180 grados.
Ahora, de las figuras que a continuación se presentan, selecciona las que son polígonos regulares.
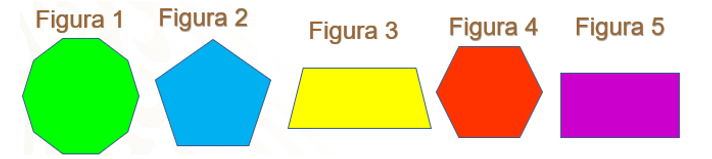
Si seleccionaste las figuras 1, 2 y 4, estás en lo correcto, debido a que un polígono regular se caracteriza por ser una figura geométrica cerrada que tiene sus lados y ángulos internos iguales. Lo que no ocurre con el trapecio y el rectángulo, que son las figuras 3 y 5.
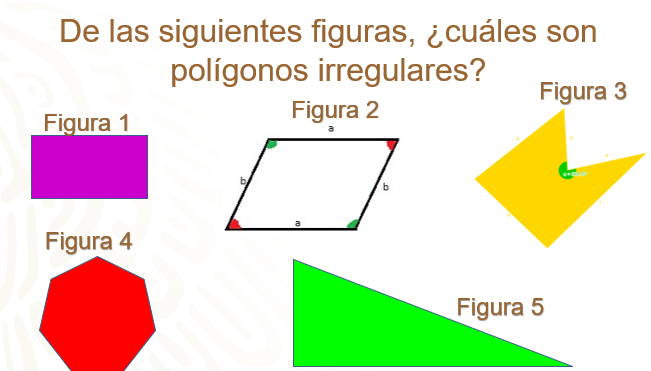
Los polígonos irregulares son las figuras 1, 2, 3 y 5. Sin embargo, estas mismas figuras también tiene otra clasificación. ¿Sabes cuál es?
Las figuras 1, 2 y 5, además de la figura 4, son polígonos convexos, ya que puedes observar que sus ángulos internos son menores de 180 grados. Por el contrario, en el polígono de la figura 3 puedes apreciar un ángulo interno mayor a 180 grados, por ello, también se clasifica como polígono cóncavo.
Ahora te presentaremos unos enunciados incompletos que hacen referencia a los polígonos. En ellos debes seleccionar la palabra que los haga verdaderos. Las palabras para elegir son vértice, diagonal, ángulo y lado.
- Un ___ es el segmento que une dos vértices consecutivos.
- Un ____ es el punto de unión de dos lados consecutivos.
- Una ___ es el segmento de recta que tiene sus extremos en dos vértices no consecutivos.
Valida tus respuestas; en el inciso “a” la palabra que completa el enunciado de manera correcta es lado, siendo el segmento que une dos vértices consecutivos; en el inciso “b”, un vértice es el punto de unión de dos lados consecutivos; por último, en el inciso “c”, la palabra correcta es diagonal, ya que una diagonal es el segmento de recta que tiene sus extremos en dos vértices no consecutivos.
Para corroborar que quedó entendido y continuar con la misma dinámica, identifica la palabra que completa de forma correcta cada enunciado de acuerdo con la imagen que se presenta.

Corrobora tus respuestas; en el inciso “a” la línea roja es un lado del polígono, en este caso el polígono tiene 5 lados con las mismas medidas, por lo que se trata de un pentágono regular; las líneas verdes son diagonales del polígono, debido a que tienen sus extremos en dos vértices no consecutivos; el inciso “c” el punto de unión de dos lados consecutivos es el vértice del polígono.
Para profundizar en el concepto de las diagonales de un polígono, te presentaremos algunos polígonos en los cuáles tienes que identificar las líneas que son diagonales.
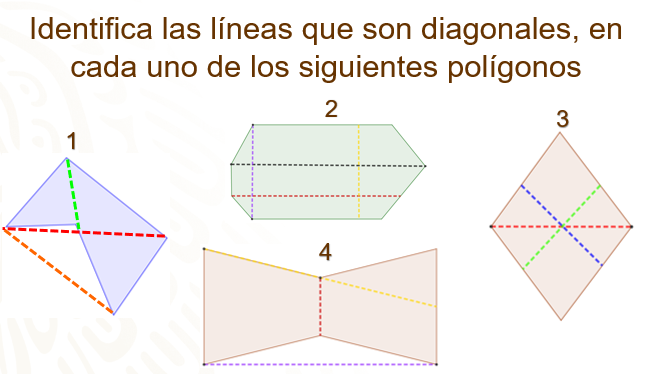
Valida tus respuestas; en el polígono 1, las tres líneas que se observan son diagonales del polígono dado que coinciden en que sus extremos son dos vértices no consecutivos; en el polígono 2, únicamente se observan dos diagonales y son la línea de color morado y la de color negro. La línea roja no es diagonal, ya que solamente uno de sus extremos se encuentra en un vértice y el otro extremo se encuentra a la mitad de un lado del polígono, la línea de color amarillo tampoco es diagonal porque no tiene sus extremos en ningún vértice; en el polígono 3 la única diagonal es la línea de color rojo, las otras líneas no se encuentran en ningún vértice de éste y, por último, en el polígono 4, la que no es diagonal es la línea de color amarillo debido a que solamente un extremo parte de un vértice y el otro extremo se encuentra a la mitad del lado opuesto.
Es importante que identifiques que una diagonal no siempre es una línea inclinada, por ejemplo, en el polígono 2 la línea de color negro es una línea horizontal y si es diagonal, por otro lado, en los polígonos 1 y 4 se puede apreciar que las diagonales también se pueden trazar externas al polígono. Esa es una de las características de los polígonos cóncavos, que al menos una de sus diagonales es externa al polígono, mientras que en los polígonos convexos todas sus diagonales son interiores.
Ahora resuelve la siguiente situación.
José tiene tarea de dibujo técnico, en la que le dejaron trazar todas las diagonales de dos polígonos regulares. Él eligió trabajar con un hexágono y un octágono. Al entregar la tarea, el profesor le dijo que estaba incorrecta, pero no le dijo en qué estaba mal, ¿qué le hizo falta o le sobra al trabajo de José?
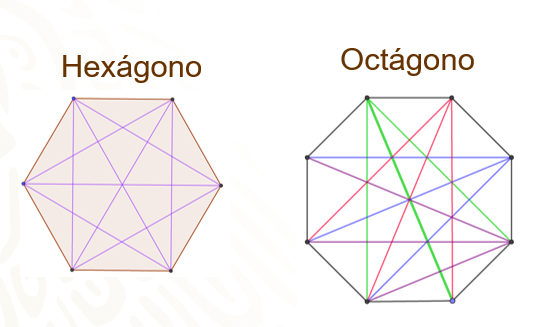
Retomando que una diagonal es el segmento de recta que une dos vértices no consecutivos del polígono, ¿cuántos segmentos debió trazar en cada polígono, para determinar todas las diagonales?, ¿qué información puede ser de utilidad para contestar a la pregunta anterior?
Considera que a partir de cualquier vértice se pueden trazar diagonales a otros vértices del polígono, excepto hacia el mismo o hacia los dos vértices contiguos, es decir, se eliminan siempre tres vértices; entonces, en el hexágono se pueden trazar tres diagonales desde un mismo vértice.
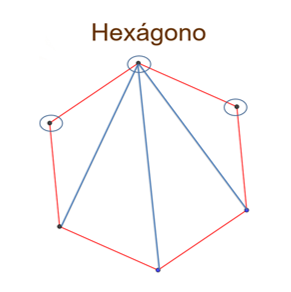
Lo mismo va a pasar con los 5 vértices restantes, entonces como son 6 vértices y en cada vértice se trazan 3 diagonales, ¿el hexágono tendrá.18 diagonales?
Al contar las diagonales, algunas se cuentan dos veces, entonces ese resultado se tiene que dividir entre dos. Por lo que si dividimos 18 entre 2 obtenemos 9, de lo que concluimos que el hexágono tiene 9 diagonales.
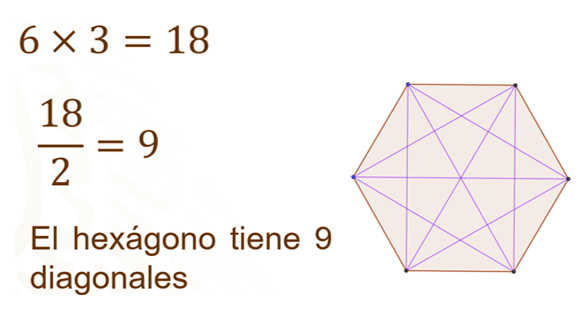
Si observas el trabajo de José al menos en el hexágono su tarea es correcta. Los datos que son de utilidad para encontrar el número de diagonales es el número de lados y de vértices del polígono. Teniendo esta información será fácil revisar la tarea de José para el caso del octágono.
Primero revisa el número de diagonales que se pueden trazar desde un vértice, y son 5; como es un octágono tiene 8 vértices, entonces multiplicamos 8 por 5, de lo que obtenemos 40. A este número lo dividimos entre 2 y da como resultado 20, por lo tanto, el octágono tiene 20 diagonales. Entonces a José le faltaron por trazar 8 diagonales más.
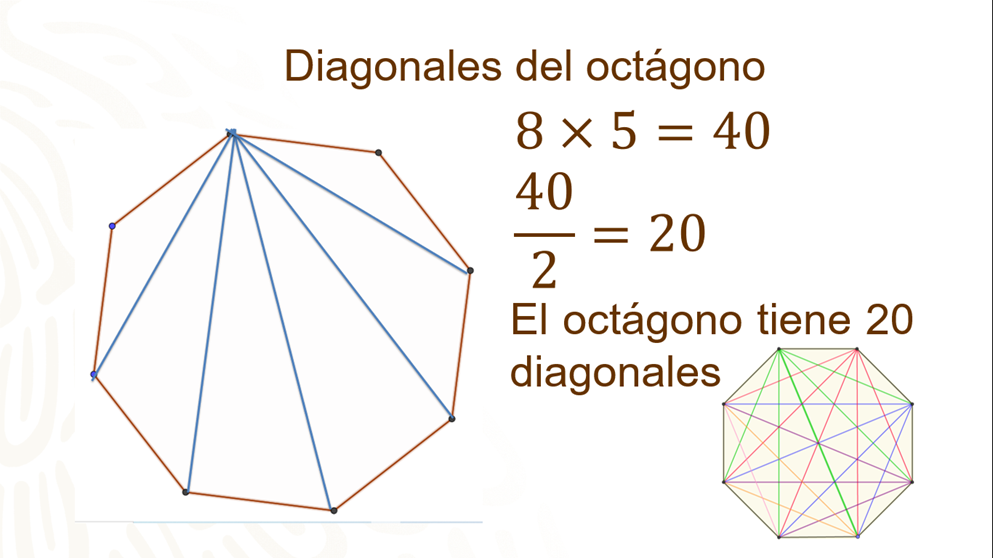
Revisando esta información se puede obtener una expresión algebraica que nos permite obtener de manera más rápida el número de diagonales de cualquier polígono.
Los ejemplos anteriores coinciden en que, al número de lados del polígono se le resta 3, y lo obtenido se multiplica por el número de lados o de vértices de dicho polígono. Luego el resultado se dividió entre 2. De esta manera, el número de diagonales se puede obtener mediante la expresión algebraica:
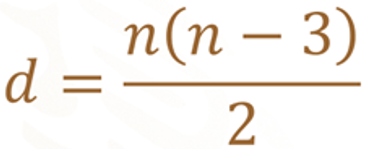
En donde n representa el número de lados del polígono.
Corrobora el resultado de las diagonales del octágono mediante esta expresión algebraica.

Se obtuvo el mismo resultado, entonces, con esta expresión se puede conocer el número de diagonales de cualquier polígono.
Para concluir esta parte de las diagonales, resuelve el siguiente cuestionamiento. Si un polígono tiene trazadas 7 diagonales desde un mismo vértice, ¿cuántos lados tiene ese polígono?
Cuando revisas el número de diagonales de los polígonos, descartas 3 vértices del polígono debido a que de ahí no se pueden trazar diagonales, entonces, si ahora tienes el dato de las diagonales, bastará con sumar 3 al número de diagonales para saber cuántos lados tiene el polígono. Por lo que, a 7 le sumas 3 y obtienes 10, por lo tanto, podemos afirmar que el polígono tiene 10 lados.
Al trazar las diagonales desde un vértice de los polígonos, también se puede conocer la suma de los ángulos internos de dichos polígonos. Cabe destacar que esto se cumple únicamente para los polígonos convexos.
Analiza un ejemplo con dos pentágonos, uno regular y uno irregular.
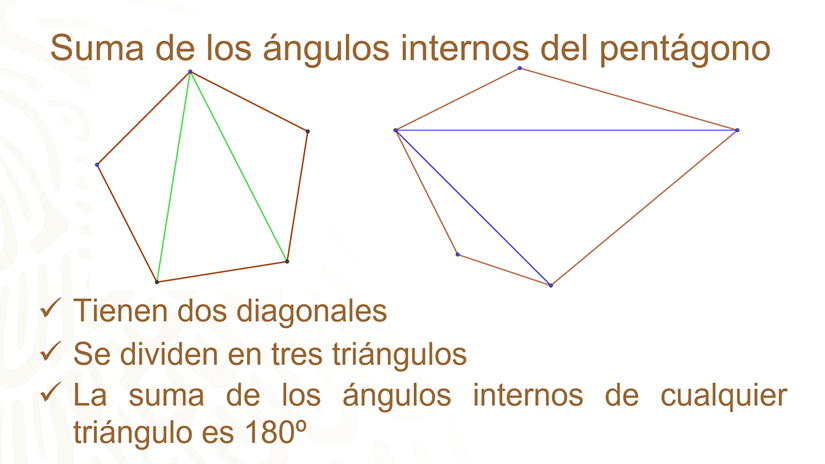
En ambos casos se han trazado sus diagonales a partir de un vértice, ¿qué observas en los pentágonos?
Se puede apreciar que ambos pentágonos quedan divididos en 3 triángulos y una de las características de los triángulos es que la suma de sus ángulos internos es 180 grados.
Con esta información, se puede deducir que, si son 3 triángulos y cada uno suma 180 grados en sus ángulos internos, para conocer la suma de los ángulos internos de cada pentágono únicamente se multiplica 180 por 3, de lo que se obtiene 540, lo que representa que la suma de los ángulos internos de un pentágono es 540 grados.
Analiza otro ejemplo, ahora con el dodecágono, es decir, un polígono de 12 lados. A partir de un vértice vas a trazar todas sus diagonales. Encontrando que tiene 9 diagonales y se divide en 10 triángulos; entonces, para conocer la suma de sus ángulos internos únicamente multiplica 180 por 10 de lo que resulta 1 800.
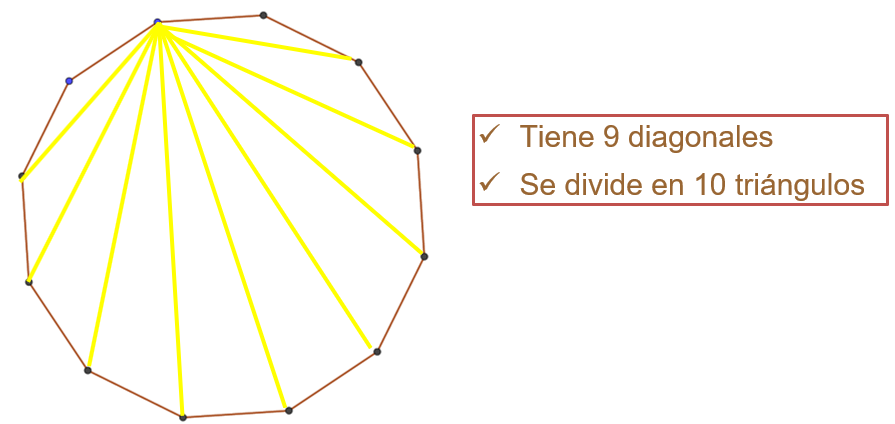
Por lo que podemos afirmar que la suma de los ángulos internos de un dodecágono es 1 800 grados. ¿Habrá alguna otra forma de conocer esta información?
Nota que, en los dos casos anteriores, al número de lados del polígono se le resta 2 y el resultado se multiplica por 180 grados, entonces se puede deducir que para conocer la suma de los ángulos internos de los polígonos se puede usar la expresión algebraica:
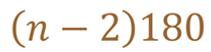
Donde “n” representa el número de lados del polígono.
Compruébalo con el pentágono, como este polígono tiene 5 lados, se sustituye en la expresión algebraica.
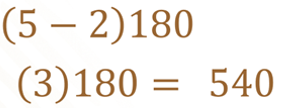
Coincide con la información anterior.
¿Habrá algún polígono tal que, la suma de sus ángulos interiores sea igual a 450 grados?
Para dar respuesta al cuestionamiento se puede hacer uso de la información anterior. Observa que en la expresión algebraica la diferencia de “n” menos 2 multiplicada por 180, “n” menos 2 representa el número de triángulos en que se divide el polígono, y siempre se multiplica por 180 para conocer la medida de la suma de los ángulos internos. Entonces, si ahora lo que nos están proporcionando es el resultado de la suma de los ángulos, pues lo que se hace es la operación inversa.
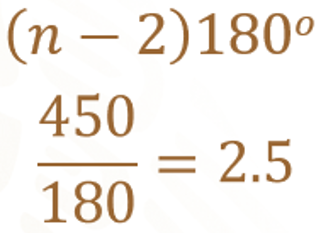
Como el resultado es un número decimal, significa que no hay dicho polígono ya que no puede haber un polígono que se divida en 2 punto 5 triángulos. Pues el polígono que se divide en 2 triángulos es un cuadrilátero y la suma de sus ángulos interiores es 360 grados y el polígono que se divide en 3 triángulos es el pentágono y la suma de sus ángulos internos es de 540 grados. Así que no hay polígono que en la suma de sus ángulos internos tenga 450 grados.
Para corroborar que comprendiste la información resuelve los siguientes cuestionamientos.
Se sabe que la suma de los ángulos internos de cierto polígono es de 900 grados. ¿Cuántos lados tiene el polígono?
En el problema se indica que la suma de los ángulos internos es 900 grados, es decir, nos indican el resultado de resolver la expresión (n-2) 180 debe ser 900.
Con esta información se puede establecer una ecuación, quedando (n–2) 180 = 900, en donde “n”, que es la incógnita o valor desconocido, representa el número de lados del polígono.
Para resolver la ecuación procedemos a eliminar paréntesis, así que multiplicamos 180 por cada uno de los términos que se encuentran dentro del paréntesis.
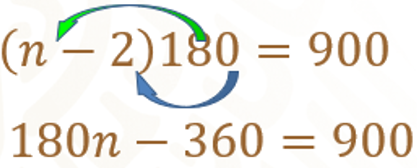
Para continuar despejando la incógnita, podemos sumar 360 en ambos lados de la ecuación.

Resolviendo se obtiene 180 n =1 260. Luego, se divide a ambos miembros de la igualdad entre 180, de lo que resulta que “n” es igual a 7.
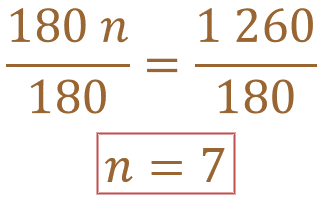
Por lo tanto, se puede decir que el polígono que cuya suma de sus ángulos internos es de 900 grados, es un polígono de 7 lados.
Resuelve otra situación.
¿De acuerdo con la información que se presenta, determina el valor del ángulo “x” que falta?, ¿cuál es tu propuesta de resolución?, ¿la información proporcionada hasta el momento te sirve para resolverlo?
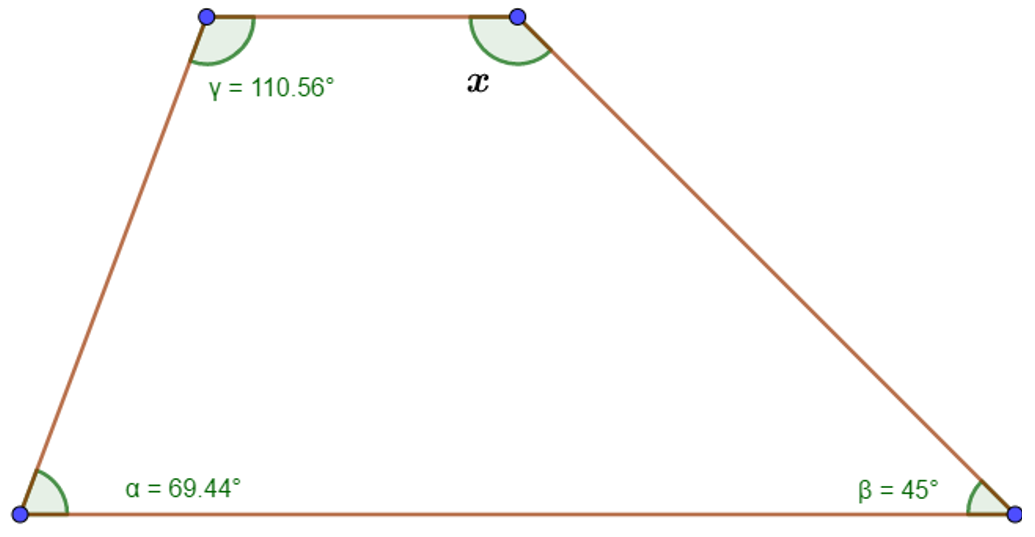
Se puede partir de trazar las diagonales desde un mismo vértice, en este caso solamente se puede trazar una diagonal y divide al polígono en dos triángulos, así que multiplicamos 180 x 2 y resulta 360, entonces la suma de los ángulos interiores de ese polígono es 360 grados.
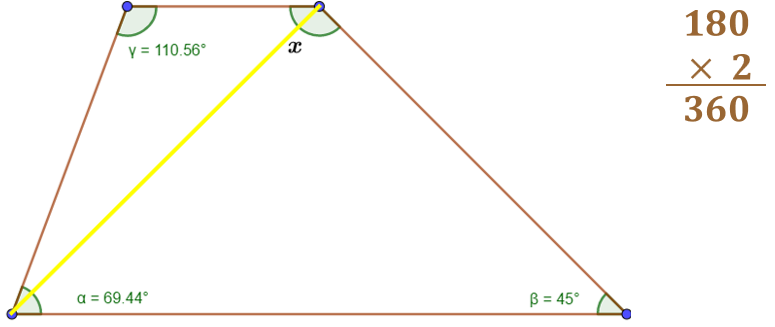
También se puede hacer uso de la expresión algebraica (n-2) 180. Al sustituir el valor de “n” por el número de lados del polígono, que en este caso es 4, se obtiene (4-2) 180, es decir, 2 x 180 que es 360, que coincide con el resultado anterior. Ahora sabemos que la suma de los ángulos debe ser 360 grados, entonces sumamos los ángulos conocidos y a continuación restamos 360, que es el total de la suma de los ángulos internos.
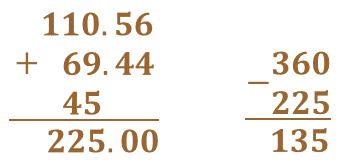
Por lo tanto, la medida del ángulo “x” es 135 grados.
Resuelve un ejercicio más. Determina el valor del ángulo “x” del siguiente polígono.
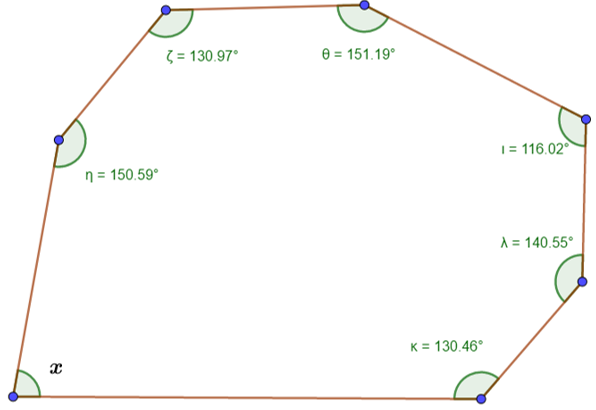
Nuevamente partimos de la expresión (n-2) 180. Los lados del polígono son 7 y sustituimos este valor en “n”.
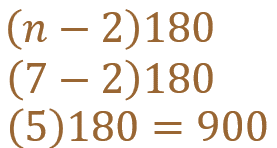
Ésta debe ser la suma de los ángulos internos del polígono.
Ahora sumamos todos los ángulos conocidos.
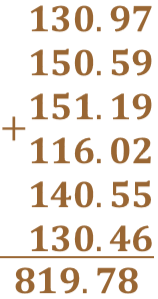
A continuación, calculamos lo que falta para 900 grados.
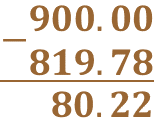
Entonces ése es el valor del ángulo faltante.
Revisa otro ejemplo, pero ahora para calcular la medida del ángulo central de polígonos regulares.
El ángulo central de un polígono inscrito en una circunferencia está formado por dos radios que unen el centro del polígono y 2 vértices consecutivos del mismo.
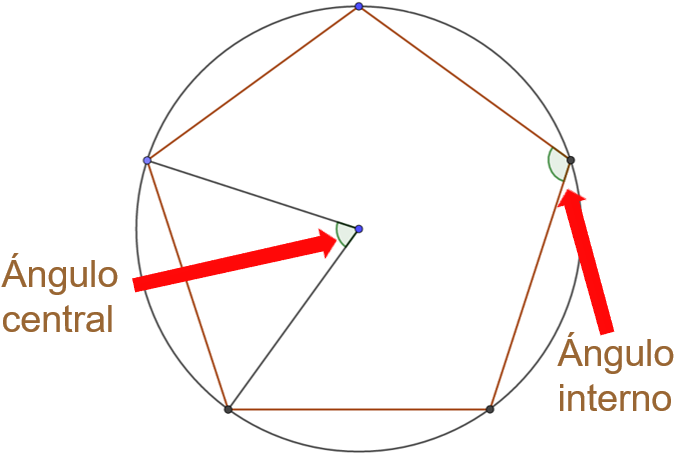
Para poder determinar la medida del ángulo central, traza los radios que van del centro a los vértices del polígono.
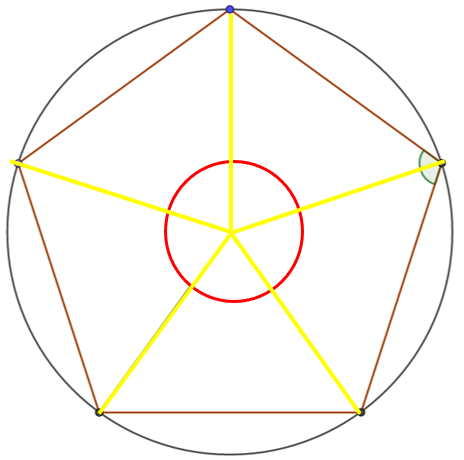
Nota que queda dividido en 5 partes iguales y en el centro del polígono se puede identificar un ángulo completo o perigonal, es decir, de 360 grados, que se muestra con rojo. Entonces para conocer la medida del ángulo central solamente se obtiene el cociente de 360 entre 5, de lo que resulta 72, por lo tanto, la medida del ángulo central del pentágono regular es de 72 grados.
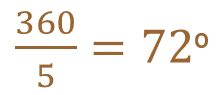
Para determinar la medida del ángulo central de cualquier polígono regular es el mismo procedimiento, por lo que se puede generalizar con la siguiente expresión algebraica, en donde “n” representa el número de lados del polígono.
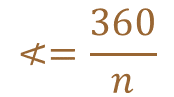
Teniendo esta información también es posible trazar cualquier polígono regular, por ejemplo, se puede realizar el trazo de un nonágono inscrito en una circunferencia con 4 centímetros de radio.
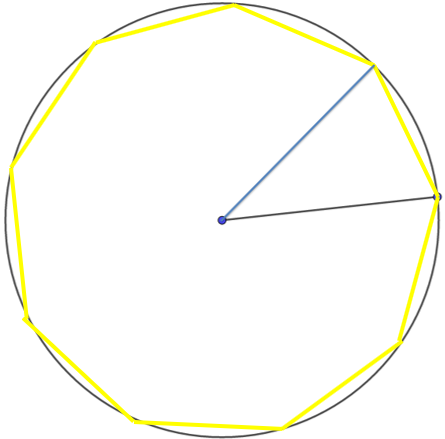
Podemos conocer la medida del ángulo central de la figura. Partiendo de la información anterior, dividimos 360 grados entre 9, ya que el nonágono tiene 9 lados. El cociente es 40 grados; esto representa que el ángulo central será de 40 grados.
Después procedemos a trazar una circunferencia de 4 centímetros de radio. Luego se marca un radio y ese mismo se toma como lado inicial para trazar un ángulo central de 40 grados. Posteriormente se trazan ángulos centrales de 40 grados, uno junto a otro. Para finalizar la construcción se unen los puntos o marcas donde los ángulos cortan a la circunferencia.
El reto de hoy:
Como reto, traza tres polígonos regulares, cada uno inscrito en una circunferencia.
Comparte tus dudas y reflexiones con tus compañeras, compañeros y docentes.
¡Buen trabajo!
Gracias por tu esfuerzo.
* Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas