Estimación

Estimación

Aprendizaje esperado: concibe las matemáticas como una construcción social en la que se formulan y argumentan hechos y procedimientos matemáticos.

Énfasis: vincular conceptos fundamentales.

¿Qué vamos a aprender?

Ten a la mano tu cuaderno de apuntes, lápiz y goma.

Se te recomienda que anotes lo que consideres importante durante la sesión y no perder detalle de la información; lleva un orden en las actividades para que puedas retomar los temas con mayor claridad.

¿Qué hacemos?

Seguramente alguna vez has estimado, por ejemplo, ¿cuántos chicles hay en una bolsa?

Y calculas, por ejemplo, que la bolsa tiene 100 chicles.

El contenido de la bosa señala que la cifra exacta es 120 piezas, así es que la estimación fue buena.

Asociar a las matemáticas como un medio para conseguir resultados “con exactitud” es una concepción simplista, mientras que, para la estimación, se le considera una interpretación limitada o ajena de las matemáticas.

Entonces, estimar un valor aproximado de los chicles en la bolsa, es parte de construir a las matemáticas. Así también es posible que en la cotidianeidad escuches argumentos como “Creo que 4 pizzas es suficiente para los invitados”; “Al evento asistieron cerca de mil personas”; “La entrega se realiza entre las 4 y las 5 de la tarde”, y “El largo de este alambre es como de 10 metros”.

Todas las expresiones antes mencionadas encierran estimaciones —y si se examina el comportamiento de estas apreciaciones—, se observa que se llegan a resultados aproximados con un cálculo mental.

La “estimación” tiene múltiples usos y campos de aplicación. Por ello es conveniente acotar su definición. Pero, ¿qué se entiende por estimación? Es dar una aproximación a una cantidad.

Aunque una estimación no se limita sólo a la aproximación o a las cantidades.

La estimación ha sido empleada en diversos contextos del cotidiano.

Se piensa, por citar algunos ejemplos, en la necesidad de calcular el dinero para ir de compras, pensar en cuál bolsa llevar al súper para sostener el mandado o calcular la hora sin necesidad de un reloj.

En las situaciones anteriores, raramente se necesitan resultados exactos.

Así se demuestra cómo emplear las estimaciones tanto en cantidades globales como en la realización de operaciones.

Existe la estimación en cálculo, referido a las operaciones aritméticas y a los juicios que pueden establecerse sobre los resultados.

Por ejemplo, una estimación del resultado de 2 345 multiplicado por 52 es 120 000, si se realiza la operación, el valor de la multiplicación es 121 940.

La otra estimación es cuando mides. Para la estimación en medida, que se refiere a los juicios a establecerse sobre el valor de una determinada cantidad o bien, la valoración que se hace sobre el resultado de una medida.

Por ejemplo, una estimación es la valoración que se realiza sobre la altura de una persona cuando se le compara con tu propia altura. Otro ejemplo es la estimación del número de personas que asisten a una manifestación.

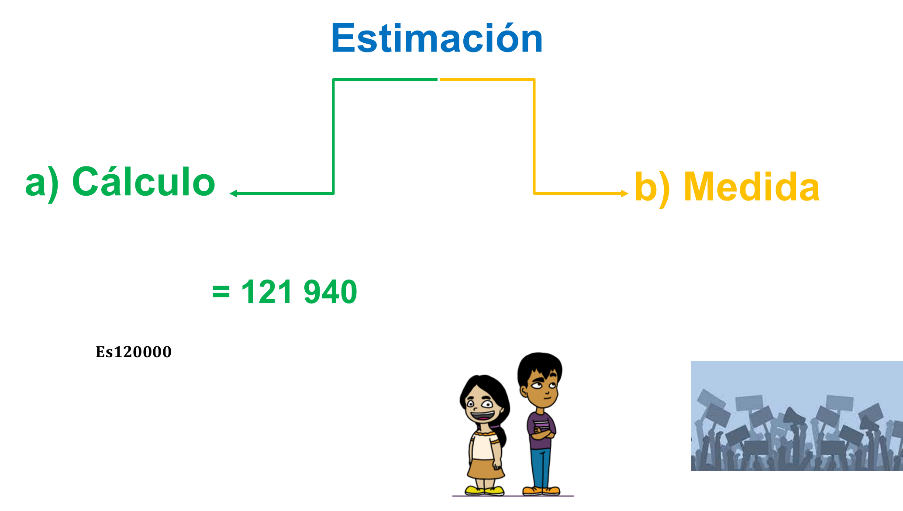
Entonces, la estimación del número de chicles en la bolsa es una estimación de medida.

Entonces en los procesos de estimación del resultado de una operación o de la medida de una cantidad, el cálculo mental tiene un papel destacado.

De hecho, la estimación produce resultados aproximados porque en los procesos de estimación se transforman o se sustituyen los datos por números más sencillos; es decir, que sean fáciles de memorizar y accesibles para las operaciones aritméticas mentales.

Pero también se puede hacer uso de papel y lápiz y de la calculadora para hacer las operaciones, porque la estimación no es cálculo mental, aun cuando se auxilie de él.

Existen varias formas de producir a partir de los datos exactos números sencillos para calcular.

Números sencillos por truncamiento. Truncar un número consiste en tomar únicamente los dígitos de la izquierda según la situación dada. Para operar con el número resultante, se puede reemplazar por ceros las cifras suprimidas cuando son valores enteros. Un truncamiento de 3 572 sería 3 570, o 3 500, o 3 000.

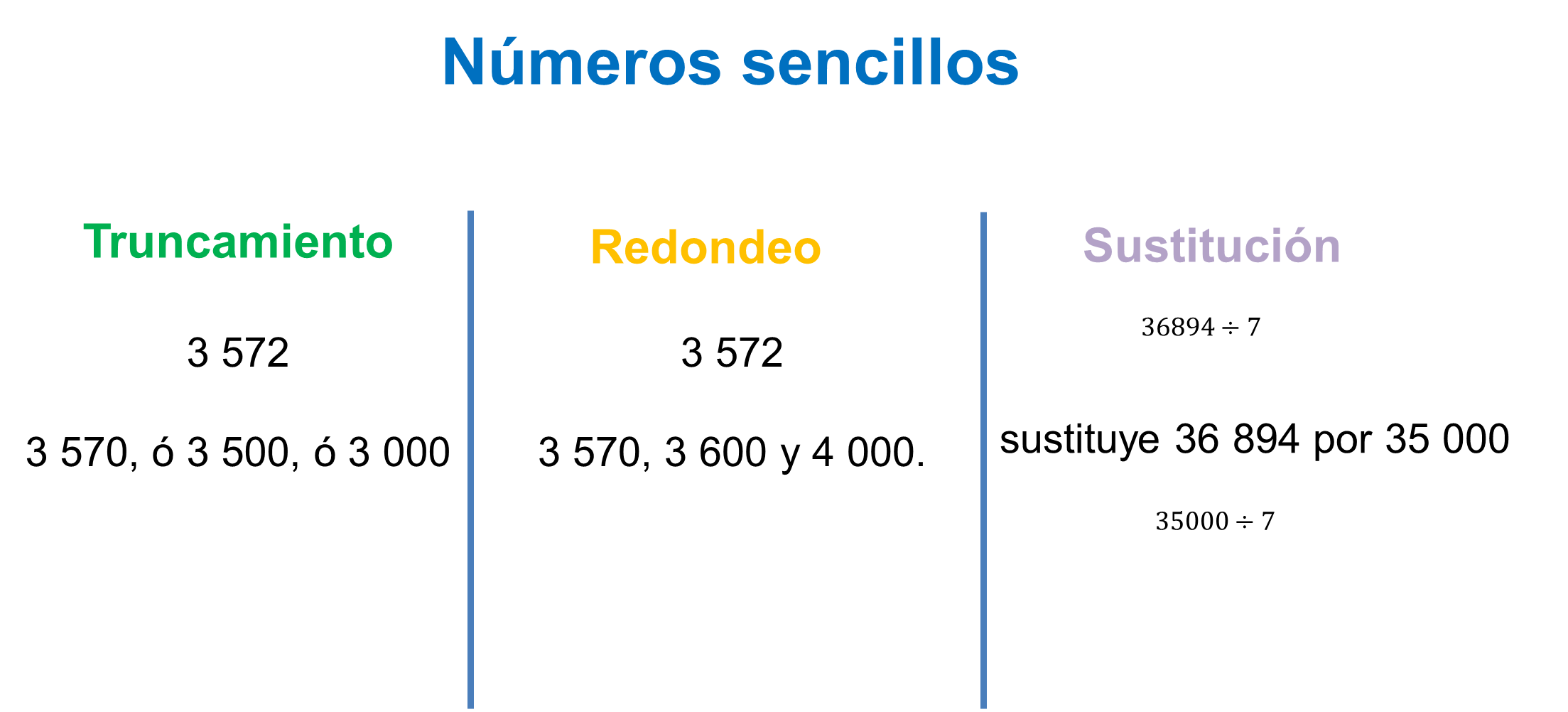
Asimismo, se puede operar con el número tal y como está, para entonces añadir los ceros al resultado; en ello se debe decidir si se trunca en la cifra de las unidades, las decenas u otras.

Números sencillos por redondeo. Redondear un número consiste en tomar sólo los dígitos de la izquierda más significativos de acuerdo con las diferentes situaciones. La condición dada es que, si la primera cifra que se desecha es 0, 1, 2, 3 o 4, entonces la última cifra se mantiene igual.

En otro caso, si la cifra elegida es 5, 6, 7, 8, o 9, la última cifra que se mantiene aumenta en una unidad respecto del número que se redondea.

En el ejemplo anterior, los redondeos de 3 572, considerando la cifra de las unidades, es de 3 570; la de las decenas de 3 600 y las de las centenas 4 000.

Mientras que los números sencillos por sustitución, cuando un dato resulta complicado para operar, puede ser sustituido por otro próximo en valor, con lo que se facilita el proceso. Por ejemplo, para obtener un resultado estimado de 36 894 entre 7, se sustituye 36 894 por 35 000 de forma que la división 35 000 entre 7 resulta sencilla de realizar mentalmente.

Pero, ¿cuál es la importancia de la estimación?

La estimación potencia la capacidad para enfrentarse a situaciones cuantitativas en el cotidiano.

De este modo, ya sabes que se realizan estimaciones sobre cálculos o medidas.

Y en concreto, que los cálculos numéricos se pueden aproximar al reemplazar un número con otros números que son cercanos y fáciles de calcular mentalmente, mientras que las mediciones se pueden aproximar utilizando referentes conocidos, como la unidad en el proceso de medición.

Para practicar estos conceptos, resuelve la siguiente actividad.

Supón que se compras 6 artículos que tienen los precios marcados en las etiquetas.

Lo que se hace es sumar 2 pesos, más 4, son 6 más 1, son 7; más 2 son 9 y más 3 son 12 pesos, pero 53 centavos y 59 hace poco más de 1 peso, y para el 0.67 y el 0.83, se consigue otro peso, al igual que con 0.56 y 0.59. Por tanto, según las estimaciones, 12 más 3, son 15 pesos.

No se está calculando la cantidad exacta a pagar, sino que estás haciendo una estimación que ayude a tomar decisiones, por ejemplo, si conviene o no llevar otro artículo.

La cantidad exacta es $15.76.

En general, al tratarse de cantidades de dinero, es conveniente que la estimación sea un tanto mayor para que no falte al momento de pagar. Para aplicar esta condición dada, resuelve una nueva situación.

¿Cuál es el resultado aproximado de dividir 203 entre 42?

Si se redondea, divide 200 entre 40, lo que resulta en 5, pero al no ser esa la operación real, sino 203 entre 42 entonces, se puede estimar un resultado de 4.5.

Si se realizan los cálculos exactos, el resultado es 4.83.

No se trata de encontrar el valor exacto, de hecho, las estimaciones pueden o no estar cerca de la cantidad, pero debe servir para tomar decisiones.

De este modo, sigue con otra situación.

Doña Mary y su familia están a 420 km de la ciudad de Puebla, hacia la cual se dirigen en su auto. Pero de repente, surge una duda, “¿Me alcanzará el dinero que tengo para llegar?”. Por lo que Doña Mari cuenta su presupuesto, un total de 1 000 pesos.

Ella sabe que su auto consume 8.6 litros de gasolina por cada 100 km —el litro de gasolina cuesta alrededor de 19 pesos; la caseta de cobro es de 179—, y en ese momento el tablero del auto indica que debe cargar gasolina.

La pregunta por resolver es ¿son suficientes los 1 000 con los que cuenta para llegar a su destino?

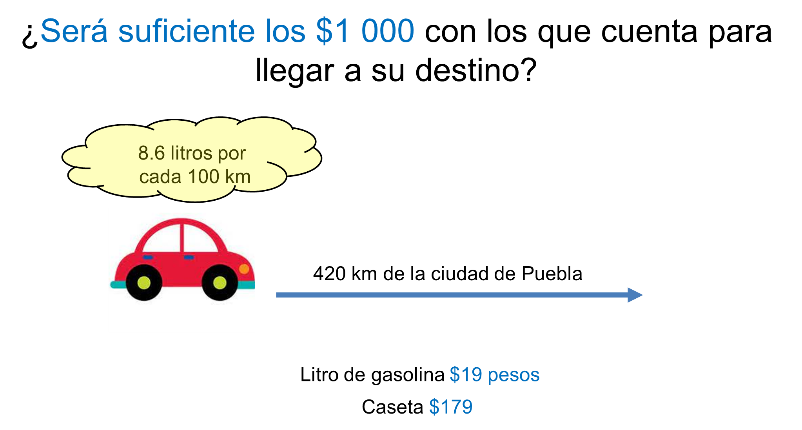
Es conveniente redondear algunas cantidades, por ejemplo, si 8.6 litros rinde para 100 km, se tienen que 9 litros rinden 100 km. Doña Mari debe recorrer casi 400 km, es decir, 4 veces más: 4 por 9 son 36 litros.

Ahora, para el gasto del combustible, se multiplica 36 por el costo de un litro de gasolina, que es de 19 pesos; estos son 800 pesos, porque se redondean las cantidades y se multiplica 40 por 20.

Por lo tanto, Doña Mari se gastará 800 pesos en gasolina, que sumados a la caseta que se redondeó a 200 pesos, se tiene un total 1 000 pesos.

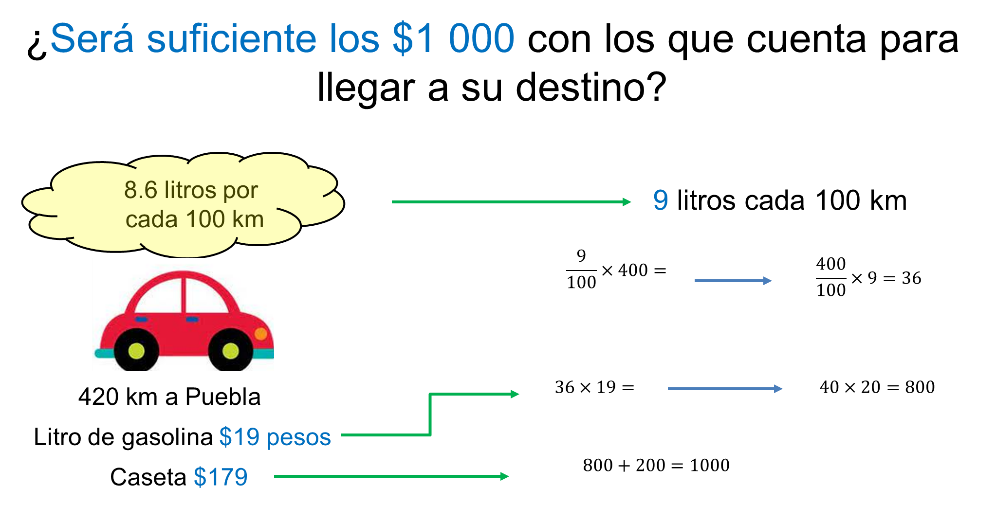
Con el dinero que tiene como presupuesto, le alcanza. Puede estar tranquila al respecto, Doña Mari.

Hasta ahora sólo se han resuelto problemas sobre estimación de cálculos. ¿Cómo se realizan las estimaciones en medidas?

La estimación en medidas, se refiere a los juicios establecidos sobre el valor de una determinada cantidad o bien, la valoración que puede hacerse sobre el resultado de una medida.

Para este caso, estima visualmente la cantidad de cubos que se muestran: Son más o menos, 15 cubos.

Y si cuentas de 6 en 6, tienes 6 por 3 igual a 18 cubos.

Con este ejemplo, está demostrado que se puede estimar un número de objetos en un área determinada al encontrar cuántos hay en un área menor, para así multiplicarlos por el número de áreas menores.

Por otro lado, cuando se estiman longitudes, se está comparando con un patrón conocido, por ejemplo, con relación a la estatura, si se conoce una estatura y se compara con la altura de un árbol, se tiene una idea de cuantas veces es mayor.

De este modo, se resuelve la siguiente situación.

En la imagen se indica que una puerta tiene una altura de 2.5 metros. ¿Cuánto se estima que mide la mamá?, ¿y cómo se justifica?

Se considera que la mamá mide 1.80 metros, porque comparando visualmente con la medida de la puerta que es 2.5 metros, puedes identificar que la diferencia es muy poca, y que la mamá realmente es alta.

Si la estimación es un juicio sobre el valor, en función de circunstancias individuales, ¿también se puede estimar que la mamá mide 1 metro?

La respuesta es no, porque sería casi la mitad de lo que mide la puerta. Sin embargo, de su hija sí se podría estimar lo anterior, que mide aproximadamente un metro.

Y si le preguntas a alguien más cuánto mide la mamá y éste responde que 2 metros, ¿quién está en lo correcto? ¿la medida de 1.80 metros o la persona que hizo la estimación de 2 metros?

Se puede pensar que ambas son correctas, porque al final se realizó una estimación; tanto 1.80 metros como 2 metros están por debajo de la altura de la puerta, reconocibles en la imagen.

En efecto, las mediciones de longitud, área, volumen y masa pueden estimarse utilizando los referentes conocidos apropiados.

A continuación, se conoce una situación adicional que ejemplifica lo antes mencionado.

Gerardo quiere pintar una barda. Si un balde de pintura alcanza para cubrir 3metros cuadrados, ¿cuántos baldes de pintura ocupará como mínimo para cubrir la barda si desconocen las medidas?

Si se supiera cuánto mide, sería una referencia para estimar cuántos metros mide de largo y alto la barda.

Pero no lo sabes. De este modo, se estima que Gerardo ya empleó un balde de pintura en la pared, y en consecuencia estima cuántos baldes o tarros usará para pintar la pared completa.

Puedes penar que aproximadamente 10 baldes de pintura.

Este fue un caso práctico de medidas. Pero ¿cómo sería un caso aplicado a la cocina? Por ejemplo, ¿te gustan los panqueques?

Resuelve una actividad en donde se realice una estimación con base al tamaño y capacidad de una taza de harina para cocinarlos.

Si para cocinar panqueques para 6 personas se necesitan 2 tazas de harina, ¿Cuántos panqueques se pueden cocinar si se tiene “un kilo y medio” de harina?

Más o menos 1 kilo de harina son como 5 tazas, por lo que “un kilo y medio” de harina son como 7.5 tazas. Entonces, alcanza como para 20 personas.

Resuelve una última situación.

El Estadio Azteca es un estadio de fútbol ubicado en la Ciudad de México, con capacidad para 87,000 espectadores, siendo así el más grande de México.

En el noticiero presentaron imágenes de las torrenciales lluvias que cayeron en la Ciudad de México, en donde el titular de la Conagua, planteó que con esas lluvias se podría llenar casi 5 veces el Estadio Azteca.

Dijo que en la alcaldía Venustiano Carranza, se precipitaron 58 litros por metro cuadrado, con un volumen de 1 millón 977 mil metros cúbicos, equivalente a 1.1 veces el Estadio Azteca.

La pregunta es, ¿cuántos litros por metro cuadrado debieron precipitarse en la alcaldía de Tlalpan, donde está ubicado el Estadio Azteca, para que el titular de la Conagua dijera que con esas lluvias se podría llenar casi 5 veces el Estadio Azteca?

Si 58 litros por metro cuadrado equivalen a llenar 1.1 veces el estadio Azteca, se multiplica 58 litros por 5 ya que 1.1 usando el redondeo sería sólo una vez la capacidad del Estadio Azteca, por lo que si multiplicas 5×8=40, 50×5=250, en total son 290 litros por metro cuadrado lo que equivale a llenar 5 veces el estadio Azteca.

Ahora responde si en Venustiano Carranza se precipitaron 58 litros por metro cuadrado, con un volumen de 1 millón 977 mil metros cúbicos, equivalente a 1.1 veces el Estadio Azteca, ¿cuántos metros cúbicos equivalen a 5 veces el Estadio Azteca?

58 litros equivalen a 1 millón 977 mil metros cúbicos entonces se quiere saber a cuanto equivale 290 litros.

El cálculo lo puedes realizar con lápiz y papel.

Si 58 litros equivalen a 1 millón 977 mil metros cúbicos, 290 litros es a “x”.

Entonces multiplica 290 por 1 millón 997 mil y obtienes 573 millones 330 mil y esa cantidad entre 58 es igual a 9 millones 885 mil metros cúbicos.

La estimación no busca dar respuestas exactas a un problema, sino dar una respuesta cercana al resultado. Como cuando se calcula el descuento de una prenda, para estimar el costo de reparación de un celular, o conocer el tiempo para llegar a un lugar, por mencionar algunos casos.

Piensa en cuáles situaciones han utilizado la estimación y comparte las reflexiones con tus familiares o amigos.

En resumen, las 4 razones por las que la estimación es útil son:

1. Imposibilidad de conocimiento de un valor exacto; como en el cálculo de un valor desconocido de manera exacta. Por ejemplo, el número de automóviles que salen de viaje un fin de semana.
2. Imposibilidad de tratamiento numérico exacto. Por ejemplo, cuando empleas en un cálculo un número decimal periódico.
3. Claridad numérica. Para dar mayor claridad y comprensión de la información a utilizar en un cálculo. Los medios de difusión masiva emplean estimaciones en lugar de cantidades exactas.
4. Facilidad en el cálculo. Son numerosas las situaciones en que la exactitud no es necesaria y es suficiente y útil un resultado aproximado; un redondeo apropiado y unos algoritmos mentales apropiados, proporcionan de manera sencilla un resultado aproximado al exacto y que resulta útil para tomar decisiones.

Lo anterior, sin dejar de emplear los cálculos matemáticos requeridos y sus reglas.

En esta sesión aprendiste que la estimación es un juicio sobre el valor del resultado de una operación numérica o de la medida de una cantidad, en función de circunstancias individuales de quien lo emite.

También aprendiste que los cálculos numéricos se pueden aproximar al reemplazar cantidades con otros números cercanos, y así facilitar el cálculo mental.

En el caso de las mediciones, se pueden aproximar utilizando referentes conocidos como la unidad en el proceso de medición.

Revisa en tu libro de texto algunas actividades que favorecen el cálculo mental, y si tienes oportunidad, resuélvelas. Por otra parte, si tienes acceso a internet u otras fuentes bibliográficas, puedes apoyarte en ejercicios de cálculo mental y practicar.

El reto de hoy:

Registra en tu cuaderno un ejemplo de alguna situación a la que te has enfrentado con respecto a la estimación en el cálculo numérico, y un ejemplo más para la estimación de medida.

Realiza otro reto. Hay un cubo que tiene los dulces de la bolsa del inicio de la sesión. Pero se necesita que estimes cuántos dulces puede contener un cubo que es tres veces mayor en sus dimensiones.

Aquí hay “_____ número” de dulces, y si el cubo fuera mayor 3 veces en su largo, ancho y espesor, entonces su volumen sería 9 veces mayor, por lo que entonces tiene 9 veces _____, que son en total “________” dulces.

Así se realiza una estimación en donde se considera la cantidad de dulces del cubo pequeño como una unidad de medida que se repite varias veces.

Explora tu libro de texto y busca qué situaciones pueden ser resueltas con lo que estudiaste.

Recuerda que, “Sin autodisciplina, el éxito es imposible”.

¡Buen trabajo!

Gracias por tu esfuerzo.

*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa*.