La probabilidad teórica
La probabilidad teórica
Aprendizaje esperado: determina la probabilidad teórica de un evento en un experimento aleatorio.
Énfasis: introducir la noción de probabilidad teórica de un evento en un experimento aleatorio.
¿Qué vamos a aprender?
“La probabilidad no se encarga de las excepciones, sino de la creencia en la existencia de un resultado, causa o motivo alternativo”.
Ésta fue una frase de Nassim Nicholas Taleb e ilustra muy bien lo que estudiarás en esta sesión, ya que seguirás profundizando en el lenguaje de la probabilidad.
¿Qué hacemos?
En algunos deportes es muy importante el resultado de los eventos azarosos, como es lanzar una moneda, por ejemplo, en los partidos de futbol soccer o de futbol americano. Entre varios de los eventos que dan inicio al partido, está el lanzamiento de una moneda, en donde el ganador de lo que comúnmente llamamos “volado”, puede decidir de qué lado de la cancha comenzar, o si comienzan pateando el balón o recibiendo el balón.
Llamamos “volado” a aquella acción de lanzar una moneda e intentar adivinar qué cara de la moneda quedará hacia arriba, antes de que la moneda detenga su movimiento.
¿Cuántas caras tiene una moneda? Y en el caso de las monedas mexicanas, ¿cómo nombramos a esas caras?
Las monedas tienen dos caras y específicamente, las monedas mexicanas tienen el águila de nuestro escudo nacional en una cara y en la otra cara, la denominación de la moneda, que nosotros conocemos como sol.
Si lanzamos la moneda es muy probable que ésta caiga sobre una de sus caras. Esto significa que en el juego del volado sólo puede haber un resultado, a menos que la moneda caiga parada y no haya resultado, o caiga en algún lugar donde no podamos recuperarla y tampoco podamos ver el resultado. Así que en el análisis que haremos, vamos a suponer que siempre veremos qué cara cae hacia arriba.
En nuestro caso deseamos que caiga águila, por lo tanto, analizaremos qué tan probable es que eso suceda.
Los casos favorables son uno, ya que sólo hay una cara águila en la moneda, entre el número de casos totales, que, por tratarse de una moneda son 2. Por lo tanto, la probabilidad de obtener águila en una moneda que no esté alterada, es un medio.
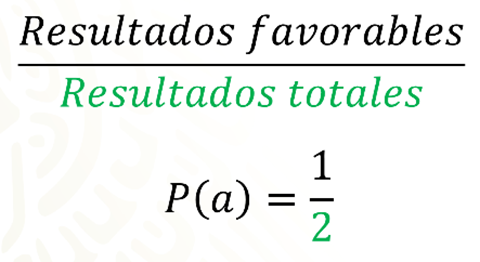
Para denotar la probabilidad utilizamos la letra “P” mayúscula y, entre paréntesis, colocamos el evento del que estamos registrando la probabilidad. En este caso, pusimos una “a” para indicar águila. Así que “P” mayúscula “a”, entre paréntesis, se lee “probabilidad de águila”.
¿Cuál piensas que es la probabilidad de obtener sol en un “volado”?
Es la misma probabilidad de que ocurra águila, es decir, también es un medio.
Otro juego muy común es el póker, en él existen cuatro mazos de cartas, identificados con un símbolo que los distingue uno de otro, están los de corazones y diamantes en color rojo, y espadas y tréboles en color negro. Cada mazo comienza con la carta llamada “As”, como se observa en la siguiente imagen.

Al reverso de cada carta se observa el mismo estampado, con la finalidad de que todas las cartas se vean iguales y no sea posible identificar qué figura se encuentra del otro lado de la carta.
Si tomamos los cuatro ases de la baraja de póker, los revolvemos muy bien, sin que veamos la figura que las distingue y colocamos las 4 cartas boca abajo sobre una mesa, es decir, con el estampado que es igual hacia arriba, y pedimos a alguien que elija una, ¿podrías adivinar de qué carta se trata?
Elije una carta entre las siguientes opciones: as de corazones, as de diamantes, as de espadas o as de tréboles; Imagina que se revuelven las cartas sin que puedas verlas y se colocan boca abajo para que intentes adivinar qué carta es la que se levantará.
Ganarás, si la carta que se levante coincide con la que elegiste.
¿Cuántas opciones en total hay para elegir?
Tienes cuatro opciones en total para elegir, colocaremos ese dato en el denominador de una fracción.
Tomando en cuenta que sólo un resultado te hará ganar, colocaremos el número 1 en el numerador, ya que sólo tienes un caso favorable para ganar.
Con esto se forma la fracción ¼ , donde el 1 representa el resultado favorable, en este caso la carta que elegiste para ganar y el 4 representa todos los casos posibles, que en este caso son: el as de corazones, el as de diamantes, el as de espadas y el as de tréboles.

Por lo tanto, la probabilidad de obtener la figura que elegiste es de 1/4 o 0.25 en su expansión decimal o 25 % en porcentaje.
Si se levanta una carta al azar, puede que sí haya sido la carta que elegiste, aunque hay más probabilidades de que no haya sido tu carta, ya que, así como tienes un caso favorable de las 4 opciones de carta, también tienen 3 cartas que no te haría ganar. Es decir, mientras tu probabilidad de ganar es un cuarto, tu probabilidad de perder es tres cuartos.
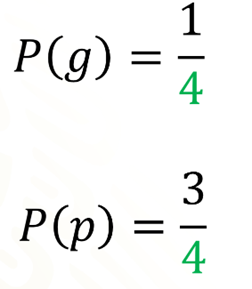
Cambiemos las condiciones del juego, ahora se revolverán nuevamente las cartas, pero en esta ocasión elegirás un color, ya sea rojo o negro, y ganarás si al levantar una carta al azar, ésta resulta del color que elegiste.
Con las nuevas condiciones del problema ¿tienes la misma probabilidad de ganar que en la situación anterior?
Para dar respuesta a la pregunta anterior, analicemos la situación. De los cuatro ases de la baraja, dos son de color rojo y dos de color negro. Entonces ¿cuántos casos favorables tienes para ganar?
Tienes dos casos favorables de un total de cuatro posibles cartas, es decir, los resultados totales son 4. Por lo tanto, colocamos el número 2 en el numerador, ya que representan las dos cartas del color que elegiste y en el denominador colocamos el número 4, que representa el total de cartas.

En esta ocasión, existe más probabilidad de que ganaras que en la actividad anterior, ya que, así como existe un medio de probabilidad de ganar, también existe un medio de probabilidad de perder.
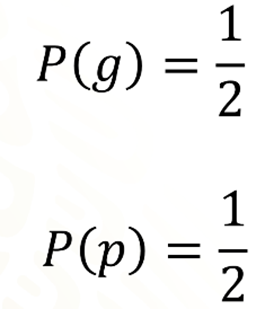
Nuevamente cambiaremos las reglas del juego, elegirás una carta y si sale esa carta, perderás, pero si no sale, ganarás. ¿Qué probabilidad tienes de ganar? Y por ende ¿qué probabilidad tienes de perder?
Con base en las nuevas condiciones existen 3 cartas que al salir cualquiera de ellas, no perderás, por ello la probabilidad que tienes de ganar es 3/4. Mientras que la probabilidad que tienes de perder es 1/4, que se cumplirá si sale la carta elegida.
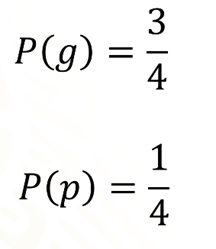
Por último, en este juego de cartas, elegirás una carta y si esta tiene una letra A en el estampado, entonces ganarás.
¿Cuántas cartas tienen una letra A en el estampado?, ¿qué probabilidad tienes de ganar?
Como ya te disté cuenta, las 4 cartas tienen una letra A en el estampado, por lo que el número de casos favorables es 4 de los cuatro resultados totales de cartas, por lo tanto, colocaremos un 4 en el numerador y un 4 en el denominador.
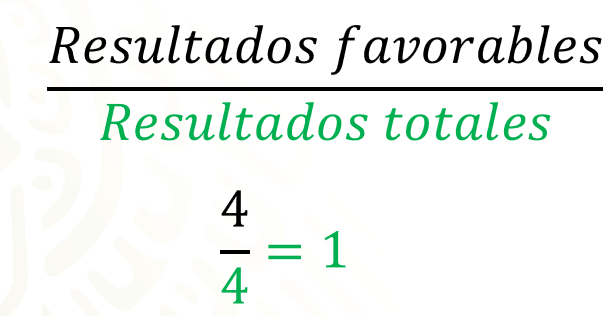
Cuatro cuartos es tu probabilidad de ganar, al simplificar la fracción obtenemos uno.
Entonces ¿qué probabilidad tienes de perder?
Debido a que se tienen todas las probabilidades de ganar, ya no quedan probabilidades de perder, es decir, la probabilidad de perder es cero.
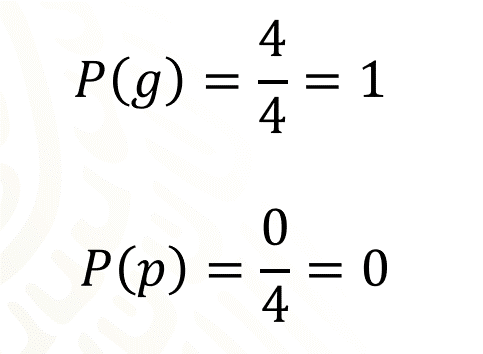
Dejemos las cartas y ahora juguemos a los dados. Para ello necesitamos dos dados, de seis caras cada uno. El juego consiste en que elegirás el número que gustes y observarás las caras que quedan hacia arriba. Sumarás los puntos de esas caras y, si la suma de los puntos coincide con el número que eligiste, entonces ganarás.
¿Qué número elegirías tomando en cuenta las condiciones del juego?, ¿elegirías el número 1? o el ¿número 45?
En primer lugar, analicemos todas las opciones posibles. Si consideramos un dado de 6 caras, las opciones posibles son, el 1, el 2, 3, 4, 5 y 6.

Seguramente no elegirías el número 1, porque ése es uno de los posibles resultados al lanzar un sólo dado, pero el juego consiste en que se lanzarán dos dados. Entonces, si consideramos el mínimo resultado de un dado, al sumarse con cualquier resultado del otro dado, ya superó al número 1.
¿Qué te parece si analizamos todos los resultados posibles del juego? Para ello usemos una tabla que nos permita organizar la información.
En la primera fila colocaremos los posibles resultados de la cara que quedará hacia arriba del primer dado, que hemos anotado con amarillo, y en la primera columna colocaremos los resultados posibles de la cara que quedará hacia arriba del segundo dado, que se escribieron con verde.
En cada casilla colocaremos la suma de las caras de los dados.
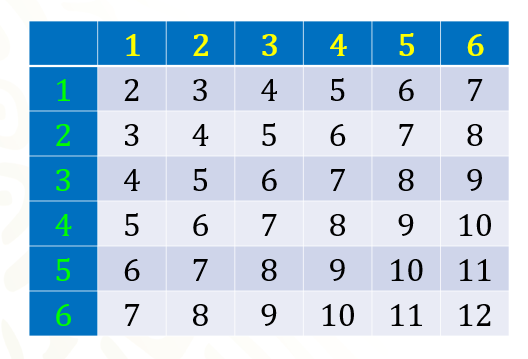
Es así que, si suponemos que el primer dado muestra en la cara superior un punto y el otro dado también muestra en su cara superior un punto, la suma de los puntos en ambas caras es 2. La suma se muestra con negro.
Pero, si el primer dado cae 1, y el segundo dado cae 2, entonces la suma de los puntos en ambas caras es 3.
Si el primer dado cae 1 y el segundo dado cae 3, entonces la suma será 4.
Cuando el primer dado cae 1 y el segundo dado cae 4, la suma es 5.
Si suponemos que el primer dado cae 1 y el segundo dado cae 5, la suma es 6.
Y si el primer dado cae 1, mientras que el segundo dado cae 6, entonces la suma es 7.
Ahora, si observas la tabla ¿es posible determinar qué suma tiene más probabilidad de salir al lanzar dos dados? Seguramente comienza a ser claro qué números aparecen más que otros.
En total hay 36 posibles resultados, los cuales se muestran en la tabla.
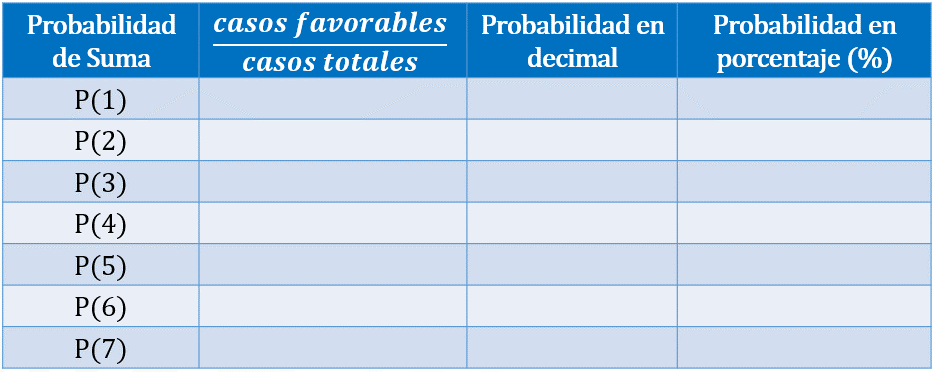
Completemos una nueva tabla donde podamos determinar la probabilidad de ocurrencia en cada una de las sumas.
En la primera columna colocaremos la probabilidad de que ocurra determinada suma, en la segunda columna expresaremos la probabilidad como fracción, es decir, el número de casos favorables entre el número total de casos.
En la tercera columna colocaremos la probabilidad expresada como decimal y por último, colocaremos la probabilidad expresada como porcentaje.
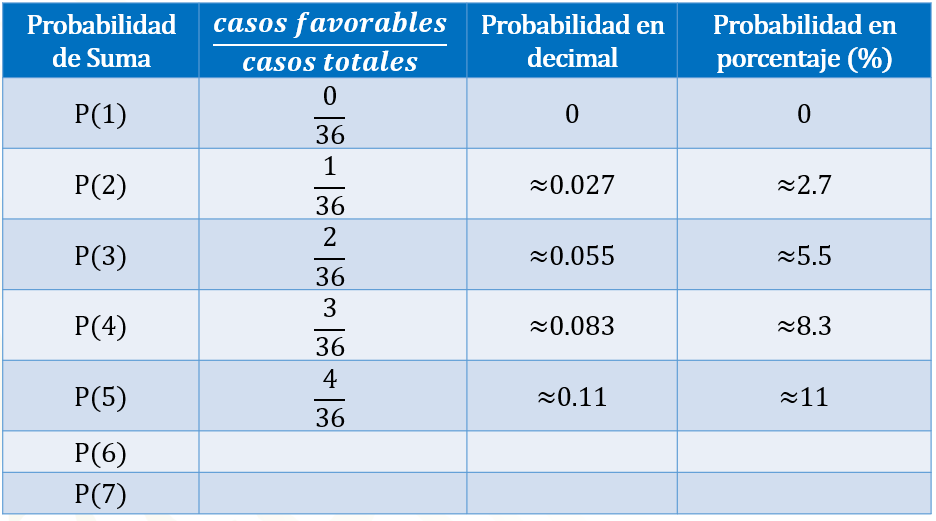
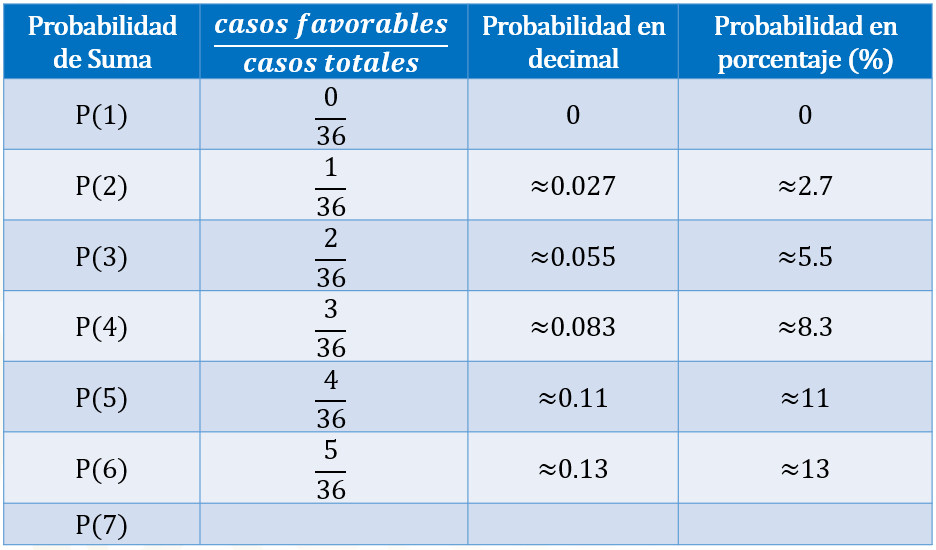
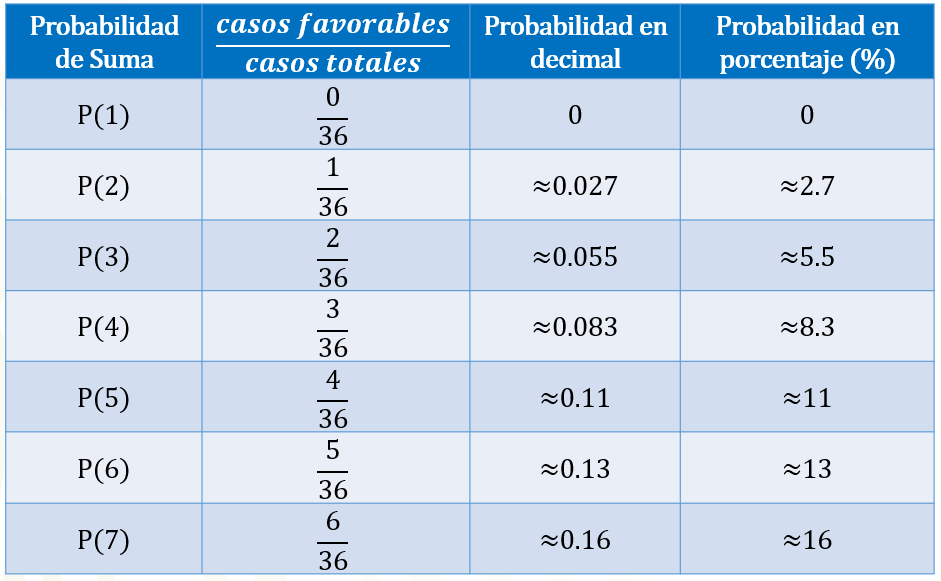
Si queremos calcular la probabilidad de que al sumar las caras superiores de los dados obtengamos uno como resultado, entonces contamos la cantidad de unos que obtuvimos en las adiciones, los cuales ocurrieron cero veces. Por lo tanto, colocamos 0 en el numerador, y 36 en el denominador, lo que representa 0 en número decimal y 0 en porcentaje.
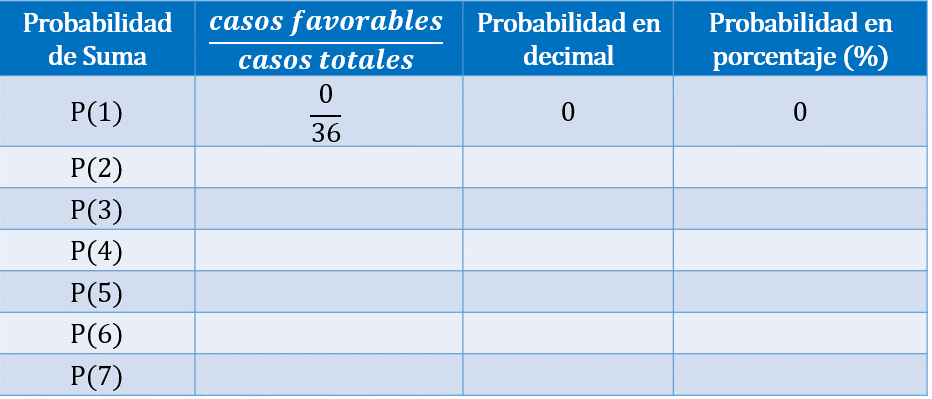
Si queremos calcular la probabilidad de que al sumar las caras superiores de los dados obtengamos 2, entonces contamos la cantidad de 2 que obtuvimos en las adiciones, lo cual ocurrió una vez. Por lo tanto, colocamos 1 en el numerador, y 36 en el denominador, lo que representa aproximadamente 0.027 en número decimal y aproximadamente 2.7 %.
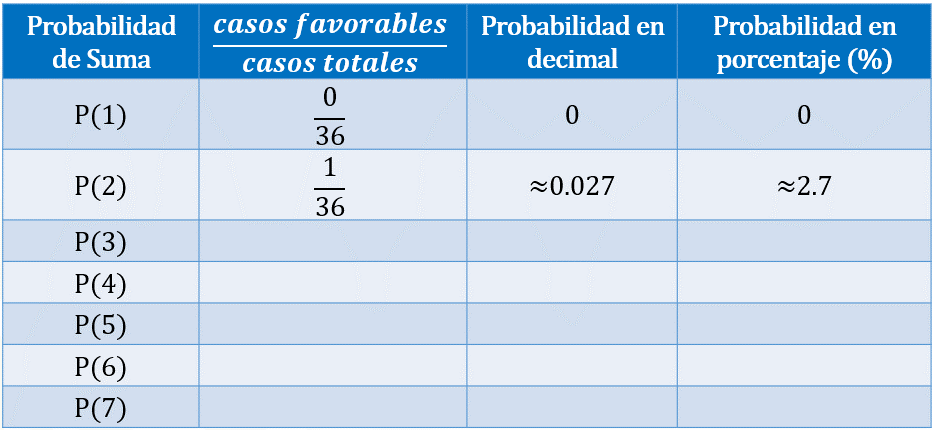
Si queremos calcular la probabilidad de que al sumar las caras superiores de los dados obtengamos 3, entonces contamos la cantidad de 3 que obtuvimos en las adiciones, lo cual ocurrió 2 veces. Por lo tanto, colocamos 2 en el numerador, y 36 en el denominador, lo que representa aproximadamente cero punto cero 55 en número decimal y aproximadamente 5.5 % en porcentaje.
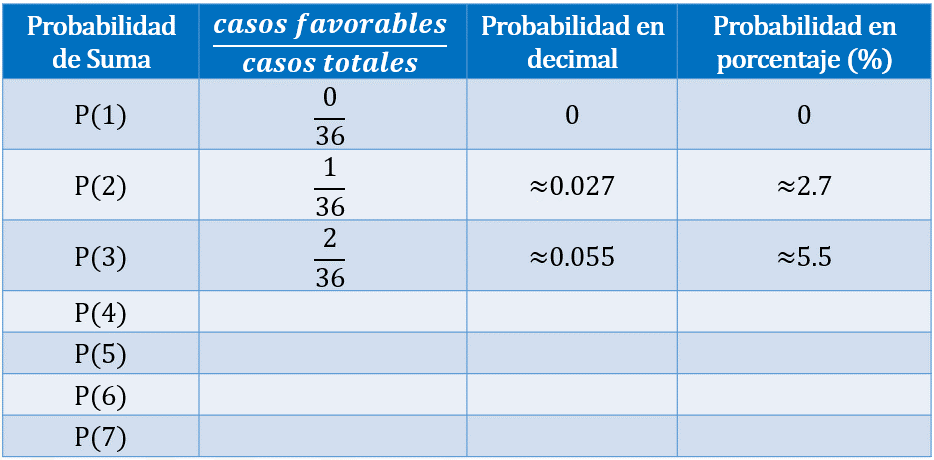
Si queremos calcular la probabilidad de que al sumar las caras superiores de los dados obtengamos 4, entonces contamos la cantidad de cuatros que obtuvimos en las adiciones, lo cual ocurrió 3 veces. Por lo tanto, colocamos 3 en el numerador, y 36 en el denominador, lo que representa aproximadamente cero punto cero 83 en número decimal y aproximadamente 8.3 % en porcentaje.
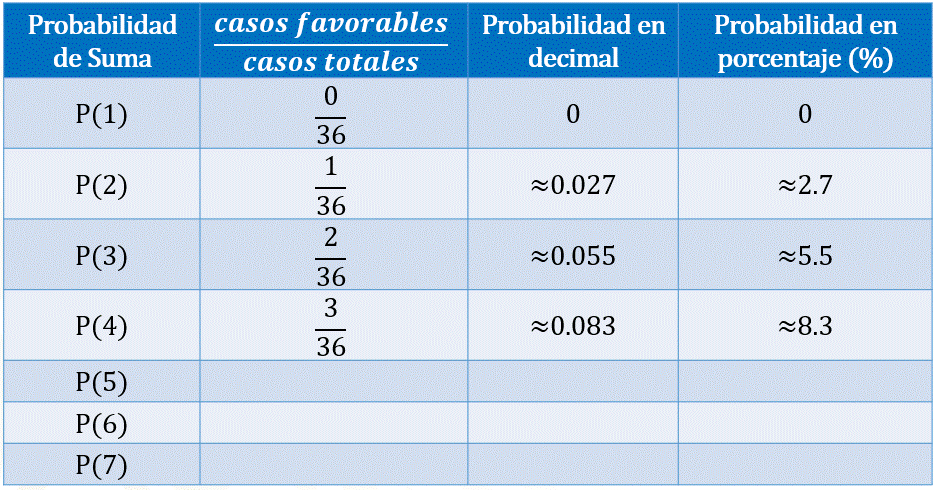
Si queremos calcular la probabilidad de que al sumar las caras superiores de los dados obtengamos 5, entonces contamos la cantidad de cincos que obtuvimos en las adiciones, lo cual ocurrió 4 veces. Por lo tanto, colocamos 4 en el numerador, y 36 en el denominador, lo que representa aproximadamente cero punto 11 en número decimal y aproximadamente 11 % en porcentaje.
Si queremos calcular la probabilidad de que al sumar las caras superiores de los dados obtengamos 6, entonces contamos la cantidad de 6 que obtuvimos en las adiciones, lo cual ocurrió 5 veces. Por lo tanto, colocamos 5 en el numerador, y 36 en el denominador, lo que representa aproximadamente cero punto 13 en número decimal y aproximadamente 13 % en porcentaje.
Si queremos calcular la probabilidad de que al sumar las caras superiores de los dados obtengamos 7 como resultado, entonces contamos la cantidad de sietes que obtuvimos en las adiciones, lo cual ocurrió 6 veces. Por lo tanto, colocamos 6 en el numerador, y 36 en el denominador, lo que representa aproximadamente cero punto 16 en número decimal y aproximadamente 16 % en porcentaje.
Si queremos calcular la probabilidad de que al sumar las caras superiores de los dados obtengamos 8 como resultado, entonces contamos la cantidad de ochos que obtuvimos en las adiciones, lo cual ocurrió 5 veces. Por lo tanto, colocamos 5 en el numerador, y 36 en el denominador, lo que representa aproximadamente cero punto 13 en número decimal y aproximadamente 13 % en porcentaje.
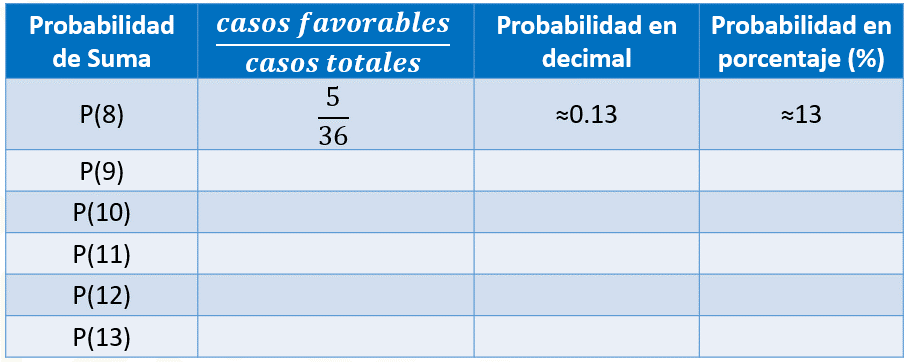
Si queremos calcular la probabilidad de que al sumar las caras superiores de los dados obtengamos 9, entonces contamos la cantidad de nueves que obtuvimos en las adiciones, lo cual ocurrió 4 veces. Por lo tanto, colocamos 4 en el numerador, y 36 en el denominador, lo que representa aproximadamente cero punto 11 en número decimal y aproximadamente 11 % en porcentaje.
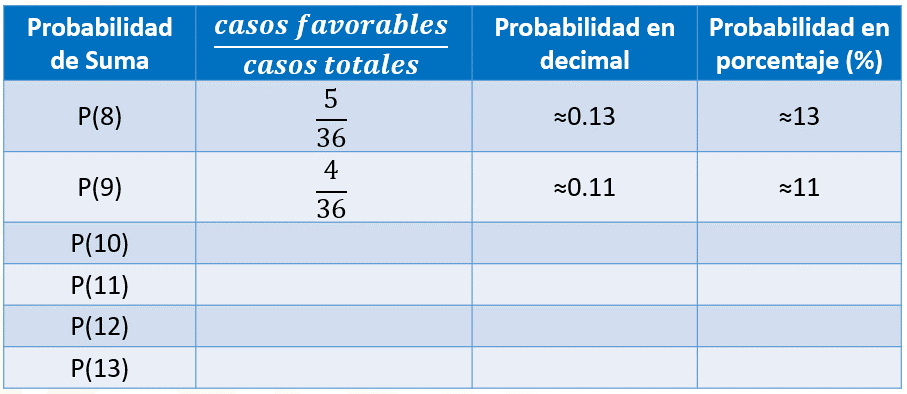
Si queremos calcular la probabilidad de que al sumar las caras superiores de los dados obtengamos 10, entonces contamos la cantidad de dieces que obtuvimos en las adiciones, lo cual ocurrió 3 veces. Por lo tanto, colocamos 3 en el numerador, y 36 en el denominador, lo que representa aproximadamente cero punto cero 83 en número decimal y aproximadamente 8.3 % en porcentaje.
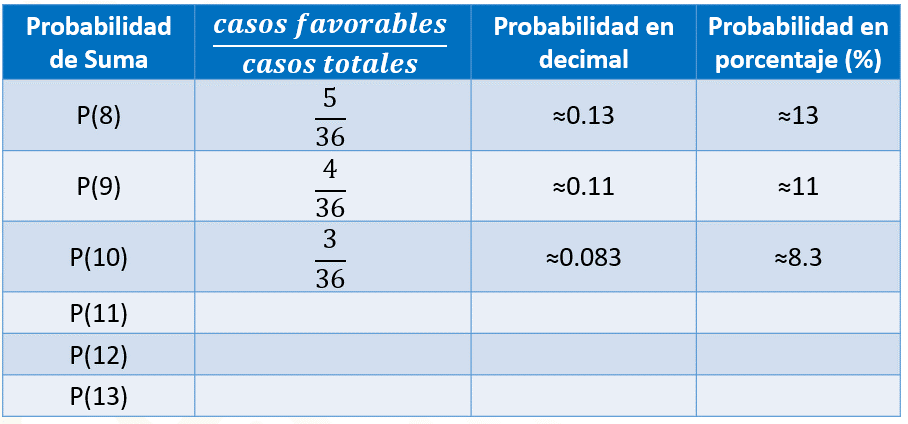
Si queremos calcular la probabilidad de que al sumar las caras superiores de los dados obtengamos 11, entonces contamos la cantidad de onces que obtuvimos en las adiciones, lo cual ocurrió 2 veces. Por lo tanto, colocamos 2 en el numerador, y 36 en el denominador, lo que representa aproximadamente cero punto cero 55 en número decimal y aproximadamente 5.5 % en porcentaje.
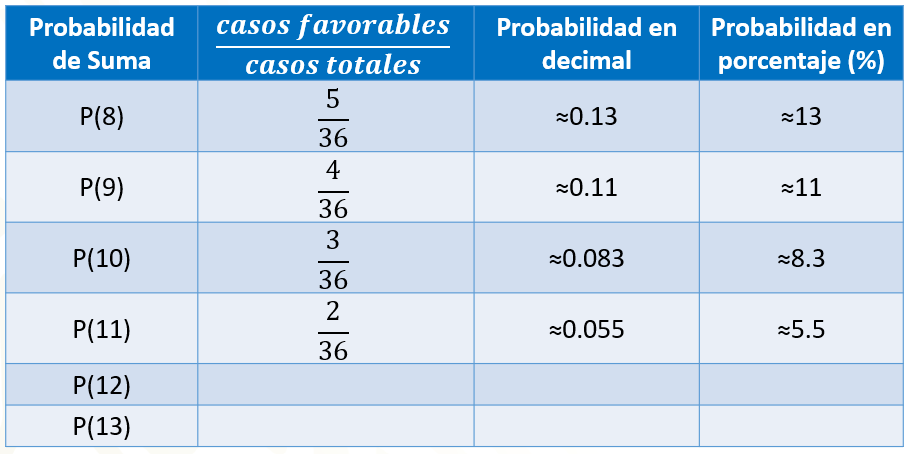
Si queremos calcular la probabilidad de que al sumar las caras superiores de los dados obtengamos 12, entonces contamos la cantidad de doces que obtuvimos en las adiciones, lo cual ocurrió una vez. Por lo tanto, colocamos 1 en el numerador, y 36 en el denominador, lo que representa aproximadamente cero punto cero 27 en número decimal y aproximadamente 2.7 % en porcentaje.
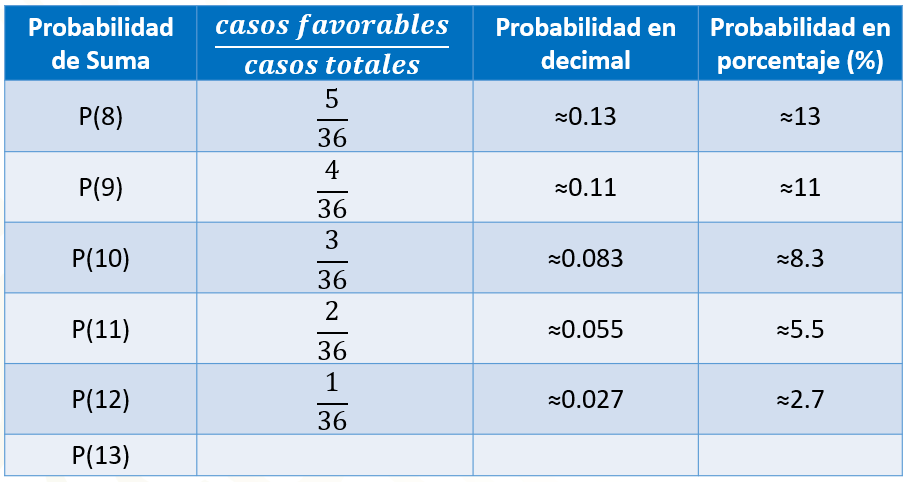
Si queremos calcular la probabilidad de que al sumar las caras superiores de los dados obtengamos 13, entonces contamos la cantidad de treces que obtuvimos en las adiciones, lo cual ocurrió cero veces. Por lo tanto, colocamos 0 en el numerador, y 36 en el denominador, lo que representa 0 en número decimal y 0 en porcentaje.
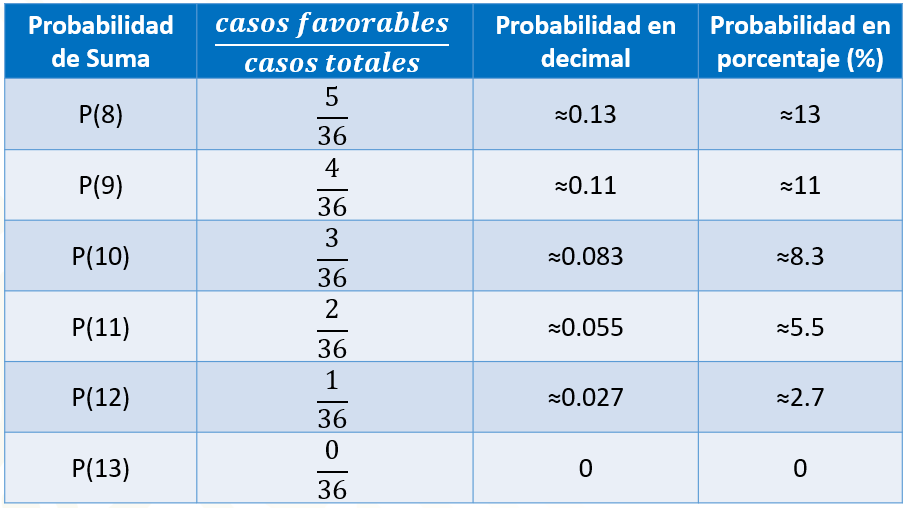
Así, puedes observar que, en este experimento, el 7 tiene más probabilidad de ocurrir y que será imposible que salga 1, 13 o cualquier resultado que no esté contabilizado en esta tabla.
¡Buen trabajo!
Gracias por tu esfuerzo.
Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas