La probabilidad frecuencial de un evento
La probabilidad frecuencial de un evento
Aprendizaje esperado: determina la probabilidad teórica de un evento en un experimento aleatorio.
Énfasis: determinar la probabilidad frecuencial de un evento en un experimento aleatorio.
¿Qué vamos a aprender?
“Siempre me recuerdo a mí mismo que lo que se observa es como mucho una combinación de probabilidades y resultados, no sólo resultados”.
Ésta fue una frase de Nassim Nicholas Taleb y en esta ocasión ilustra muy bien lo que estudiarás en esta sesión, ya que seguirás profundizando en el lenguaje de la probabilidad.
¿Qué hacemos?
¿Qué te viene a la mente cuando escuchas la palabra “probabilidad”?
Piensa unos segundos en ello. Seguramente cuando escuchas la palabra “probabilidad” vienen a tu mente palabras como: azar, ganar, perder, empatar, posible, imposible, poco probable, medianamente probable, muy probable e incluso puede llegues a pensar en la palabra “suerte”.
En esta sesión hablaremos de la probabilidad frecuencial de un evento y aquellas personas que piensan en la suerte sólo se están dejando llevar por los cálculos de una probabilidad frecuencial.
Comenzaremos con un ejemplo:
Imagina que va caminando por la calle y encuentras 1 moneda tirada, y miras a todos lodos y no hay alguna persona cerca a la que se le pudiera haber caído. Pensarás que fue debido a la “suerte”, pero, analicémoslo matemáticamente. En realidad, no tenemos idea de cuál es la probabilidad de encontrarnos una moneda, así que vamos a hacer un experimento e ir ajustando para llegar lo más cercano que podemos al valor que estamos buscando.
En primer lugar, no podemos controlar el hecho de encontrarnos dinero en la calle, por lo tanto, depende del azar.
En segundo lugar, hagamos un registro y supongamos que hoy nos encontramos dinero en la calle, podríamos registrarlo de la siguiente manera:
En este caso, el numerador la cantidad de casos favorables y en el denominador los casos totales.
Es importante que NO asociemos a “los casos favorables” como aquello que nos beneficia o favorece, sino a aquellos que cumplen con las condiciones del problema o de lo que se analiza, por ejemplo, en este caso particular es encontrar dinero.
También pudimos haber considerado como caso a analizar la probabilidad de NO encontrar dinero, y nuestros casos favorables contabilizarían cada ocasión que NO encontremos dinero.
Bueno, y si sólo contáramos esta ocasión para nuestro cálculo de la probabilidad, tendríamos que poner que como número de casos totales sólo hay uno. Así que, va 1 en el numerador. Pero recuerda que esto está muy incompleto, tenemos que ver qué pasa en las demás ocasiones para encontrar una mejor aproximación.
En el denominador registramos los casos totales, como es el primer día transcurrido o analizado, entonces registramos también el número 1.
En la siguiente columna realizamos la operación transformando nuestra fracción a su expansión decimal o en su caso al entero. Que en este caso particular se obtiene dividiendo el uno entre el uno, lo cual da como cociente uno.
En la última columna transformamos el número decimal o entero a porcentaje, el cual se obtiene multiplicando la expansión decimal por 100 por ciento, lo cual nos da un 100 por ciento como resultado.
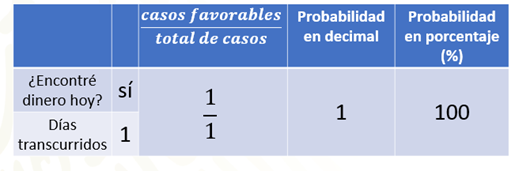
Pongamos especial atención a lo que ese 100 por ciento puede representar en el contexto del problema.
¿Qué significa que la probabilidad sea del 100 por ciento?, ¿podemos considerar que la probabilidad de encontrar una moneda en la calle es del 100 por ciento?, ¿si salimos mañana a la calle, es seguro que encontremos una moneda tirada?
En la tabla anterior trabajamos bajo una suposición, supusimos que nos encontramos una moneda, pero ahora ampliaremos la tabla.
Colocaremos los datos que nos ha tocado vivir. Nos preguntamos si encontramos una moneda ayer, y no la encontramos. Recuerda que seguimos suponiendo que sí encontramos una moneda hoy.
Siguiendo con nuestra aproximación, debido a que no encontramos una moneda ayer, nuestra cantidad de casos favorables continúa siendo uno y la cantidad de casos totales serán dos. Entonces la probabilidad es de un medio, que en su forma decimal representa 0.5 y en su expresión como porcentaje, representa el 50 %. Pero, recuerda que nos estamos aproximado y sólo el resultado final será el más parecido a lo que queremos.
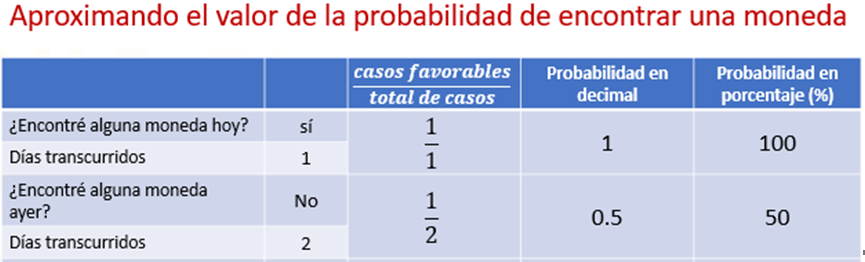
¿Qué significa que la probabilidad sea 50 por ciento?, ¿consideras que la probabilidad de encontrar una moneda tirada en la calle es del 50 por ciento?, ¿por qué si el primer día teníamos el 100 por ciento, ahora sólo tenemos el cincuenta por ciento?
Anota tus respuestas a estas preguntas y durante esta sesión estudiarás más elementos que permitan validarlas o refutarlas.
Ahora, nos preguntamos si encontramos una moneda tirada en la calle anteayer, en este caso tampoco encontramos una moneda anteayer. Por lo que el número de casos exitosos continúa siendo 1, y la cantidad de casos totales es 3, por eso colocamos un 1 en el numerador y un 3 en el denominador es decir un tercio. La representación decimal de la fracción es 0.3 periódico, y su aproximación en porcentaje es del 33.3%.
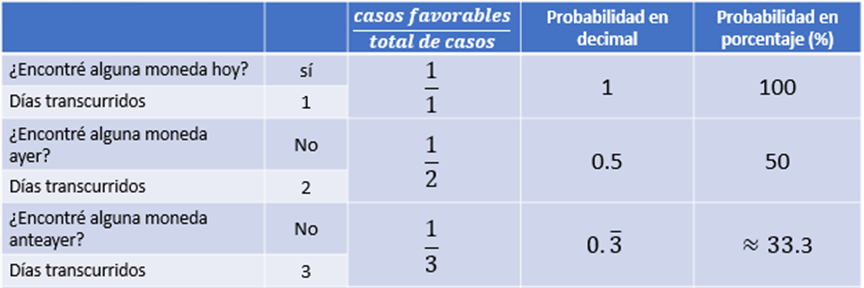
¿Qué observas respecto al porcentaje que acabamos de calcular comparado con el del primer y el del segundo día?
Como pudiste darte cuenta, el porcentaje va disminuyendo.
Ahora nos preguntamos: ¿hemos encontrado alguna moneda en las últimas dos semanas? En este caso, no hemos encontrado alguna otra moneda, además de la del primer día. Por lo tanto, colocamos un 1 en el numerador que representa nuestra suposición inicial y en el denominador el 14 que representan los casos totales de las dos semanas, tomando en cuenta que cada semana tiene 7 días. Al convertir un catorceavo a decimal obtenemos aproximadamente 0.071 que, en porcentaje, es aproximadamente 7.1%.
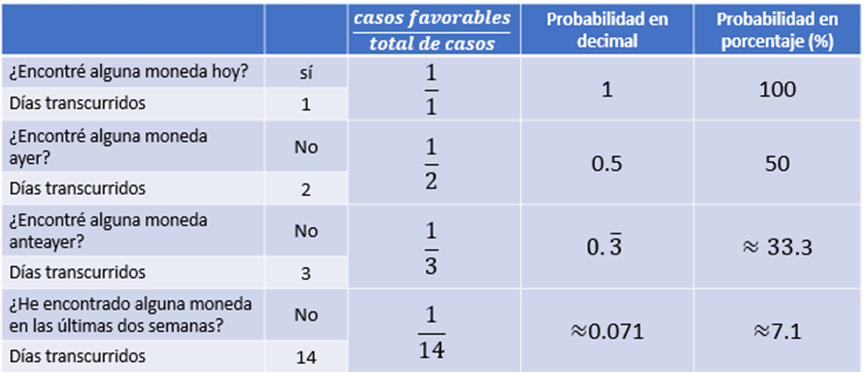
¿Notas cómo, al aumentar el número de casos, nuestras aproximaciones a la probabilidad de encontrar una moneda van disminuyendo comparando con nuestra primera aproximación?
Por último, en este caso no hemos encontrado una moneda en treinta y un días, además de la encontrada el primer día. Por esa razón, seguiremos colocando un 1 en el numerador y 31 en el denominador.
Al convertir la fracción a decimal obtenemos aproximadamente 0.032, que al convertir a porcentaje es, aproximadamente, 3.2%
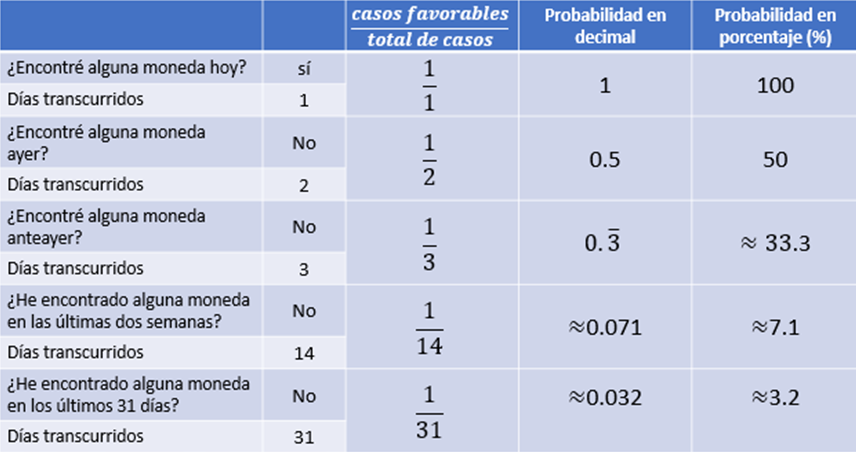
Observa cuánto disminuyó del 100 por ciento que teníamos al inicio a 3.2%
Si consideramos que el 100% es la probabilidad real de encontrar una moneda tirada en la calle, entonces diario encontraríamos una moneda, ¿qué tan cierta te parece esta afirmación?
El análisis que acabamos de hacer es una aproximación a lo obtenido en la probabilidad frecuencial, que registra los resultados provenientes de algún fenómeno azaroso y entre más datos se tengan más se acercará a la probabilidad clásica, misma que es motivo de estudio de otra sesión.
La probabilidad frecuencial se registra como el número de casos favorables, entre el número de casos totales.
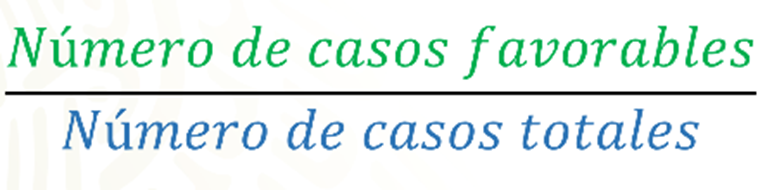
Analicemos otro caso y nuevamente tendrás que imaginar la situación.
En las calles de algunos lugares, es común que existan perros callejeros, animalitos que no tienen un hogar y que caminan por las calles. Algunas personas amablemente colocan recipientes con agua y algunas croquetas afuera de sus casas, para que esos animales se alimenten.
Imagina cómo sería la reacción de un perrito callejero que encuentra por primera vez un recipiente con agua y comida. Registremos el hallazgo de la comida en una tabla similar a la que empleamos para analizar el hallazgo de la moneda.
Recuerda que esta situación es hipotética no sabemos si la persona que coloca la comida fuera de su casa lo hará siempre, en algún momento podría salir de vacaciones, cambiar el domicilio, olvidar hacerlo, entre otras razones que pudieran evitar la constancia de la ayuda.
Y agregaremos otra condición a este análisis, lo estudiaremos desde la perspectiva del perro que deambula por las calles.
Existieron personas que hace muchos años realizaron estudios de condicionamiento en animales, colocando comida en algún lugar, y el animal no esperaba encontrar comida en el mismo lugar al siguiente día. Fue a través de una repetición de varios días cuando el animal se condicionó a que en determinado lugar encontraría siempre algún estímulo o comida.
Así que, desde esta perspectiva, el perro que camina por las calles, encuentra comida el primer día, por lo que colocaremos un 1 en el numerador y un 1 en el denominador. Al realizar la operación resulta 1 y en porcentaje, 100%. Esta es nuestra primera aproximación y seguramente no será muy buena.
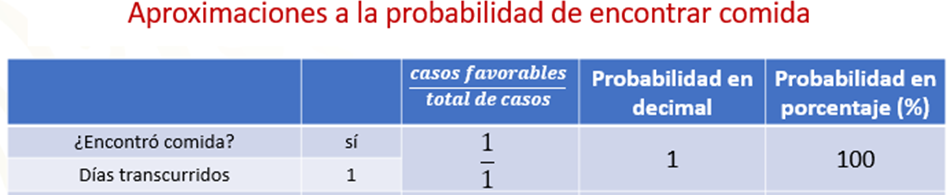
Es interesante saber que, aunque hasta el momento es el 100 % de probabilidad, el perrito aún no está condicionado para reconocer que diario encontrará la comida en ese lugar.
Supongamos que, en el segundo día, el perro que aún camina por esa calle, encuentra comida en el mismo lugar, entonces colocaremos un número 2 en el numerador y un número 2 en el denominador, ya que fueron 2 casos favorables de un total de 2 casos.
Al realizar la operación nuevamente es 1 y el porcentaje es 100 %
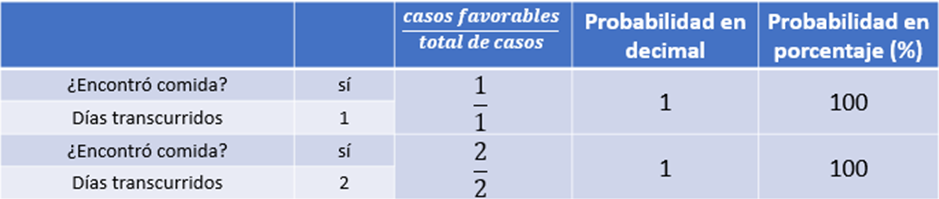
Ahora supongamos que la persona mantuvo su constancia durante una semana de siete días y diario colocó agua y croquetas en la puerta que da a la calle, y el perrito comió diariamente. ¿Qué colocaremos en la fracción que representa esta situación?
Colocaremos 7 en el numerador y 7 en el denominador que continúa siendo equivalente a 1 entero, y es equivalente a 100 %
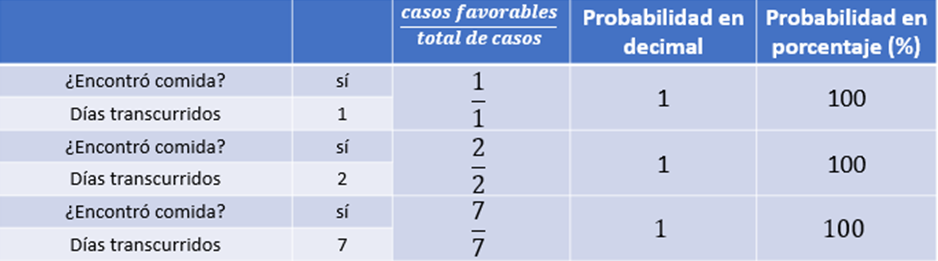
A estas alturas, puede que el perro ya esté condicionado y sabe que encontrará comida en ese lugar.
En las siguientes dos semanas la persona no pudo colocar comida, ya que el jueves y viernes salió por un viaje de negocios.
Tomando en cuenta lo anterior, ¿qué colocaremos en el numerador?
Seguramente ya te disté cuenta que ahora colocaremos 12 ya que en 2 días no colocaron comida. Por lo tanto, son 12 casos favorables de 14 totales, lo cual es aproximadamente 0.85 en su expansión decimal y, aproximadamente, 85%
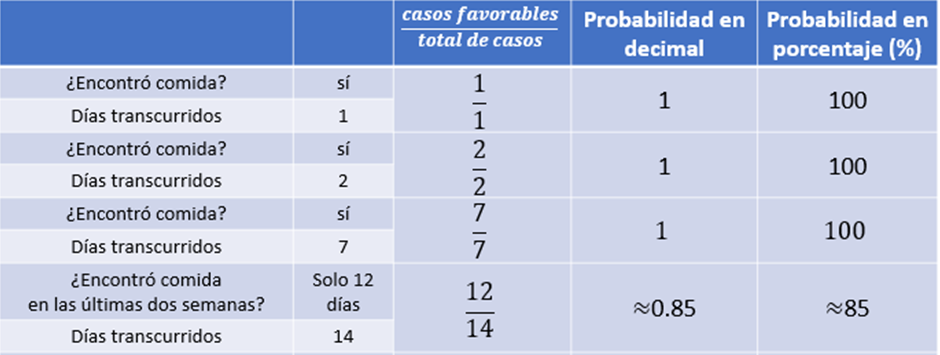
En los últimos 31 días, la persona salió a su casa que tiene cerca de una playa ya que hubieron 2 días de asueto, el viernes y el lunes, por lo que tampoco colocó comida esos cuatro días del fin de semana largo. ¿Qué número deberemos colocar en el numerador?
Ahora colocamos 25 ya que, a los 2 días anteriores que no colocó comida, adicionamos estos 4 días que tampoco la colocó.
La representación decimal de la fracción es, aproximadamente, 0.80 y su equivalencia en porcentaje es, aproximadamente, 80 %
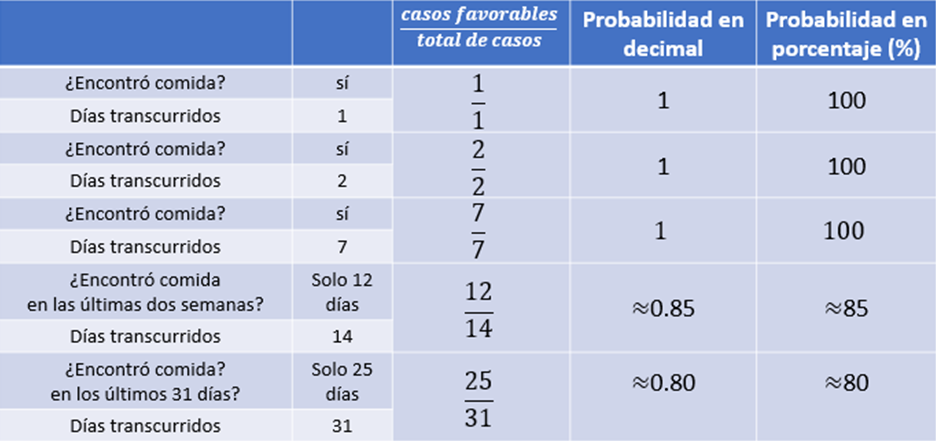
Desde nuestro punto de vista como observadores, podemos decir que, en el registro que realizamos, la probabilidad de que colocaran comida en esos 31 días fue, aproximadamente, del 80 %, lo cual, comparado con el planteamiento de encontrar una moneda en la calle es mucho mayor.
Analiza el siguiente video, observando con atención la manera en que realizan el registro de los resultados del evento.
- Los valores de la probabilidad
Repliquemos el experimento de lanzar una moneda. Para ello usaremos una tabla como la que observaste en el video, en donde las primeras dos filas corresponderán al registro de resultados en caso de que caiga sol y las últimas dos filas al registro de resultados en caso de que caiga águila. Colocaremos una “x” dependiendo del resultado que caiga y, posteriormente, registraremos la probabilidad frecuencial de ese evento, mientras que en las filas del resultado que no fue favorable también haremos el registro correspondiente.
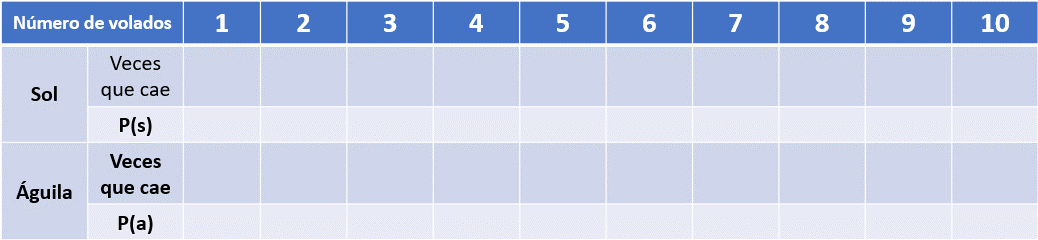
Al lanzar la moneda cayó sol. Ahora debemos registrar el resultado en las dos primeras casillas, colocando una “x” en la fila “veces que cae”, mientras que en la probabilidad de que caiga sol colocaremos un 1 en el numerador porque fue un caso favorable para el evento “probabilidad de caer sol” y un 1 en el denominador; mientras que en la casilla de águila no colocaremos algo y eso significará que en el numerador colocaremos un 0 y un 1 como denominador.
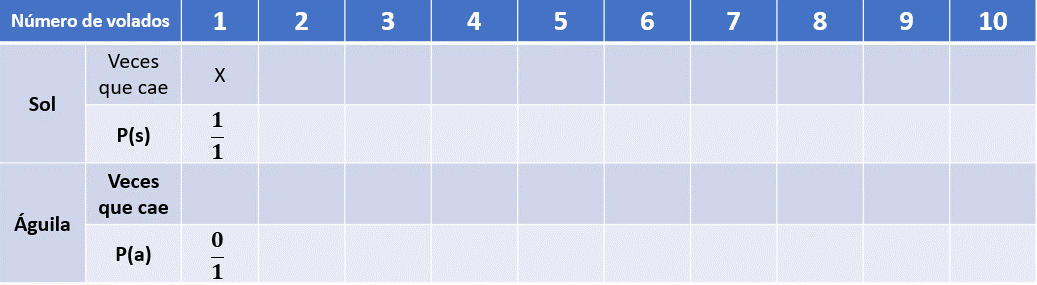
Observa que nuestra primera aproximación a la probabilidad frecuencial de que caiga sol sería de 1 sobre 1 lo cual es equivalente a 100 %. Y al sumarse con el 0 sobre 1, de la probabilidad de que caiga águila, suman cien por ciento.
Al realizar el experimento por segunda vez, volvió a caer sol, por lo que registraremos un 2 en el numerador y un 2 en el denominador, lo cual, en su representación como porcentaje es 100 por ciento. Y colocamos un 0 sobre 2, en las filas del lanzamiento de águila, ya que aún no cae águila.
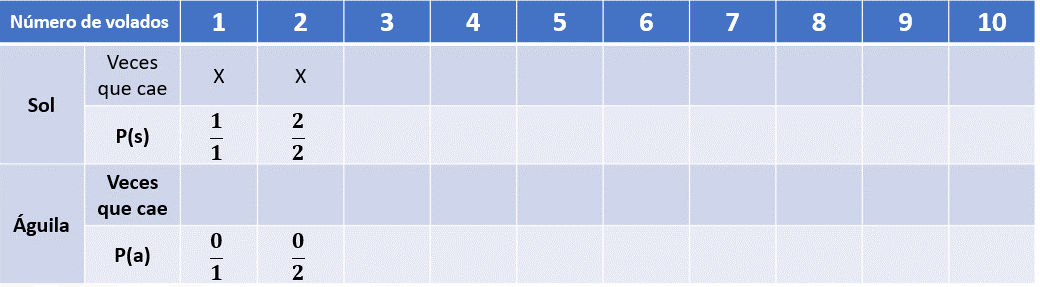
Observa que la suma de 2 medios más 0 medios sigue siendo 1 o, su equivalente, que es 100 %
Al lanzar la moneda por tercera vez cayó sol de nuevo, por lo que colocaremos un 3 en el numerador y un 3 en el denominador, en las filas de los lanzamientos de sol y en las filas de los lanzamientos de águila continuaremos colocando un 0 en el numerador y ahora, un 3 en el denominador.
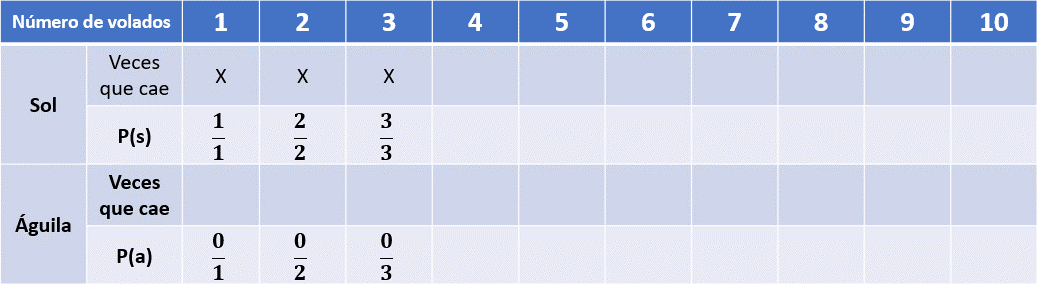
La suma de estas dos fracciones sigue siendo 1.
Para el cuarto lanzamiento cayó águila, así que colocaremos un 3 en el numerador y un 4 en el denominador, porque ya no salió sol y esto no permite seguir adicionando a los resultados de esa fila, así que la cuenta de resultados favorables se detiene en esas filas, pero el número total de resultados sigue incrementándose mientras sigamos realizando el experimento.
En las filas de los resultados del águila comenzamos el conteo de casos favorables así que colocaremos el 1 en el numerador y 4 en el denominador.
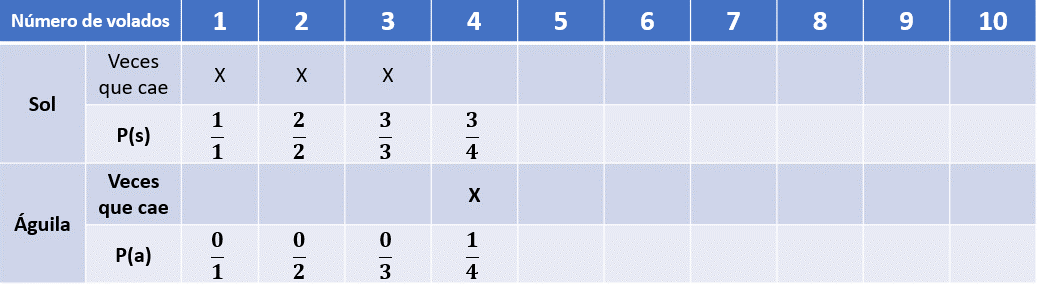
Observa que, aunque tuvimos un resultado distinto a los anteriores, las fracciones conservan su suma, es decir, 3 cuartos, que corresponde a la probabilidad de sol, más un cuarto, que es la probabilidad de águila, es igual a 1 y esto es equivalente a 100 %
Continuamos lanzando la moneda hasta realizar un total de 20 lanzamientos, obteniendo los siguientes resultados.
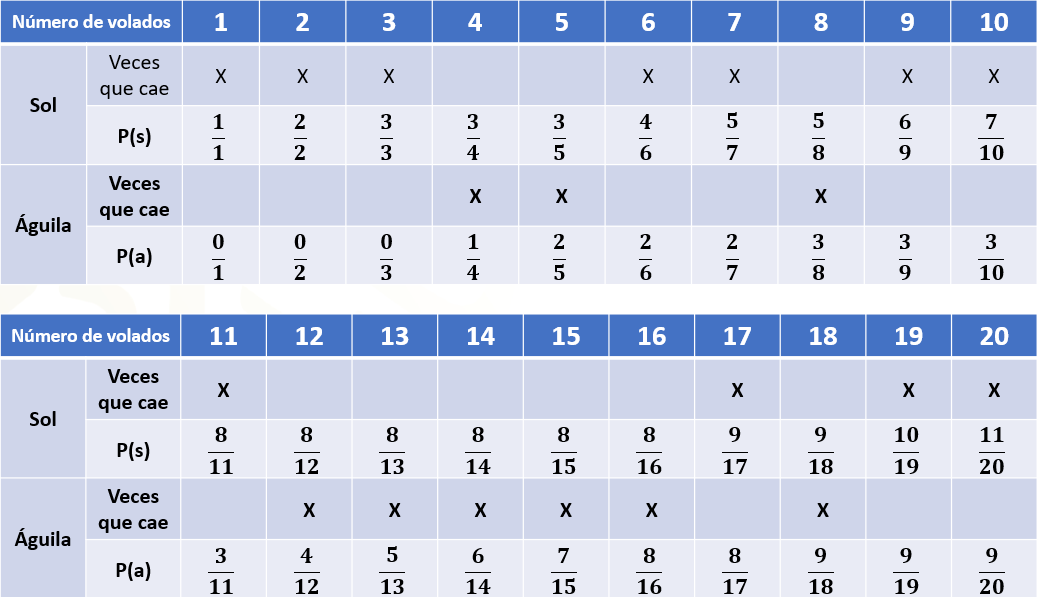
Como puedes observar, en todas las columnas, la suma de las fracciones es igual a 1, es decir, la probabilidad de que algo ocurra más la probabilidad de que algo no ocurra es igual a 1 o a 100 %.
El reto de hoy:
Realiza tu propia tabla y lanzamientos. Compárala con estos resultados, ¿qué tanto variaron?, ¿por qué ocurre esto?
Si es posible, comparte tus resultados y argumentos con tu profesora o profesor en tu trabajo a distancia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas