Probabilidad
Probabilidad
Aprendizaje esperado: calcula la probabilidad de ocurrencia de dos eventos mutuamente excluyentes.
Énfasis: conocer el desarrollo de la probabilidad.
¿Qué vamos a aprender?
Se te pide tener a la mano tu cuaderno, lápiz y goma.
¿Por qué es importante el estudio de la probabilidad?
La probabilidad permite construir modelos, desarrollar procedimientos para calcular y estimar las posibilidades de que ocurra un evento en situaciones donde interviene el azar o hay un grado de incertidumbre.
Su importancia es creciente en diversas áreas del conocimiento, por ejemplo: En ciencias básicas como la Física, la Química y la Biología, los modelos probabilísticos han favorecido a la comprensión de los fenómenos naturales.
No es entonces una exageración afirmar que conocer algunos elementos de probabilidad y estar familiarizados con el razonamiento probabilístico, es necesario tanto para el especialista como para el ciudadano informado.
Los conceptos de la Teoría Elemental de la probabilidad son ricos en resonancias intuitivas. En el cotidiano, se tiene que valorar y tomar decisiones en circunstancias donde hay incertidumbre o interviene el azar.
Debido a ello, se desarrollan ciertas intuiciones acerca de los fenómenos probabilísticos —y aunque estas intuiciones son con frecuencia inexactas o se apoyan en concepciones no siempre correctas—, proporcionan un comienzo para afinarlas y acercarse a formulaciones matemáticas más precisas.
El estudio de la probabilidad se presta para lograr un ambiente de estudio participativo. Puedes abordar algunos problemas por medio de la exploración empírica de situaciones aleatorias.
Asimismo, puedes formular hipótesis, contrastar tus expectativas con los resultados que se presentan experimentalmente, y producir y discutir tus propias explicaciones.
Estas explicaciones te ayudan al desarrollo de las nociones matemáticas.
¿Qué hacemos?
Pascal, Fermat y el Caballero de la Meré son pioneros en “Los inicios de la probabilidad”.
El origen del estudio de la probabilidad está asociado a los nombres de Blais Pascal y Pierre Fermat.
Al parecer, el Caballero de la Meré, un hombre culto aficionado a los juegos de azar, planteó ciertos problemas de juego a Pascal y éste a su vez, los discutió con Fermat por correspondencia en el año de 1654.
El siguiente problema fue conocido como el “Problema de los puntos” o “De la división de la apuesta”.
Dos personas compiten en un juego hasta completar un cierto número de puntos. Cada una tiene la misma oportunidad de hacer un punto; aquel que los complete primero se lleva la totalidad de la apuesta.
Pero si el juego tiene que interrumpirse antes de que algún jugador complete los puntos ¿Cómo se debe dividir la apuesta?
Por ejemplo, se tienen a dos personas: Llamémosles A y B, que juegan a los volados.
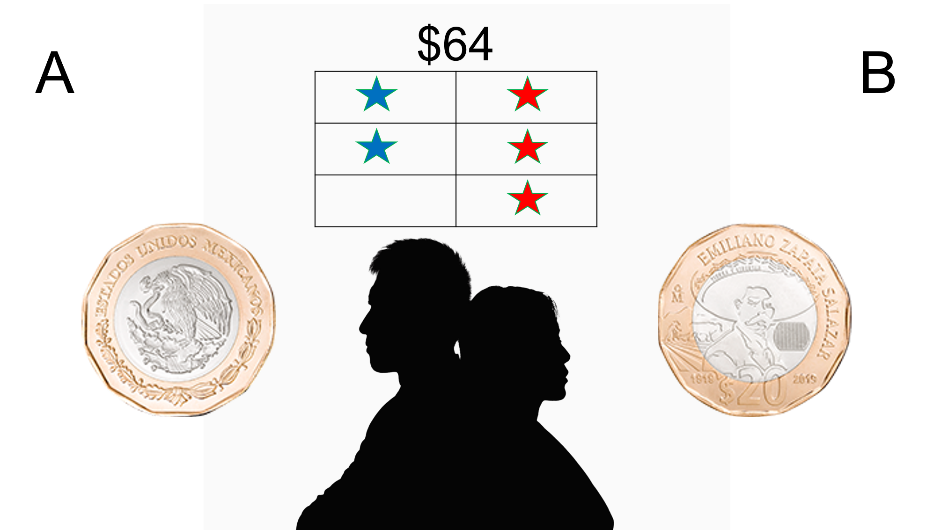
Si sale águila, “A” gana un punto; si sale sol, “B” gana un punto; juegan varios volados y el que complete primero tres puntos, gana una apuesta de 64 pesos.
Pero después de tres volados, cuando “A” lleva dos puntos y “B” lleva un punto, el juego se interrumpe.
Entonces ¿Cómo se debe dividir la apuesta?
Primero, se descarta la solución inmediata que argumenta “que se reparta mitad y mitad”, porque es probable que “A” protestará, ya que él lleva la ventaja y exigiría que se le compense con una mayor parte de la apuesta.
Tampoco es viable otra solución inmediata que sugiere repartir la apuesta en partes proporcionales a los puntos acumulados. Es decir: 2/3 de la apuesta para “A”, porque lleva 2 puntos y 1/3 de la apuesta para “B” porque lleva 1.

Esta es la “solución” que proponía el Caballero de la Meré, pero tanto Pascal como Fermat estuvieron de acuerdo en que no era correcta.
Antes, se debe considerar que dicha “solución” no depende del número de puntos que se necesitan acumular para ganar la apuesta.
En una carta a Fermat, fechada el 29 de julio de 1654, Pascal comenta el método que encontró para resolverlo: “Supongamos que se juega el siguiente punto, puede suceder alguna de dos cosas: Gana A o gana B. “
Si gana “A”, entonces se completan los 3 puntos, llevándose toda la apuesta. Pero si gana B, entonces tanto A como B se llevarían 2 puntos y la apuesta se divide en partes iguales, es decir, mitad y mitad.

Por este motivo, “A” razona así:
“Yo estoy seguro de obtener, por lo menos, la mitad de la apuesta, 32 pesos, porque aún si perdiera, el siguiente punto lo obtendría. Pero la otra mitad quizás me la lleve yo, o tú, o ambos con las mismas oportunidades. Entonces, divide esta mitad entre ambos y entrégame la mitad que ya tengo asegurada.”
Por ello, “A” reclama para sí tres cuartas partes de la apuesta:
1/2 más 1/4 igual a 3/4, es decir, 48 pesos y una cuarta parte para B, es decir, 16 pesos.
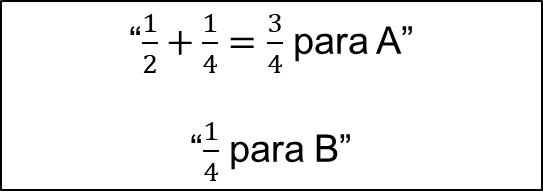
Por otra parte, la solución de Fermat es la siguiente: Se debe observar que, a lo más, en dos tiradas extras se decidiría el juego.
Supón que necesariamente se juegan esos dos puntos; se señala con “a” cuando el punto lo gana A y con “b” cuando lo gana B.

Todos los posibles desarrollos del juego son los siguientes: “aa”, “ab”, “ba”, “bb” y de éstos, en 3 casos ganaría A, contra un solo caso en el que ganaría B.
Por esto, la fracción de la apuesta que se debe llevar “A” es 3/4, es decir, 48 pesos y 16 pesos para B.
Realiza la primera actividad, desarrolla el problema de la división de la apuesta cuando “A” y “B” juegan a 4 puntos en una apuesta de 64 pesos, teniendo como situación que el juego se interrumpe cuando “A” lleva 3 puntos y “B” 1.
El cálculo de la probabilidad está basado en algunos conceptos fundamentales, mismos que se desarrollan a lo largo de tu educación secundaria.
Se identifican a continuación las diferencias entre un experimento aleatorio y uno determinista, que son parte de estas ideas fundamentales.
Observa el siguiente video del inicio al minuto 01:41.
- ¿Qué es el azar? ¿Qué es aleatorio?
https://www.youtube.com/watch?v=ViMZbNG5Klw
Analiza algunos procedimientos para registrar y visualizar datos, realizar conjeturas, verificar tendencias y otros requerimientos.
El uso de diagramas de árbol y arreglos rectangulares —así como de otras técnicas sencillas de conteo para enumerar casos—, son habilidades que se deben desarrollar.
Los diagramas de árbol, además de facilitar la enumeración de los resultados que pueden presentarse al realizar una experiencia aleatoria, proporcionan una imagen visual de los desarrollos posibles de la experiencia.
Para ello es importante que te acostumbres a escribir en cada rama las probabilidades, tal y como se muestra en el siguiente ejemplo.
Se tienen cinco canicas blancas y cinco negras en una caja.
Extraes al azar una canica de la caja y se deja de lado, para después extraer una segunda canica también al azar.
¿Cuáles son los posibles resultados?
Utilizando un diagrama de árbol, del punto de partida se tienen dos ramificaciones: 5 de las 10 canicas son blancas y 5 canicas son negras.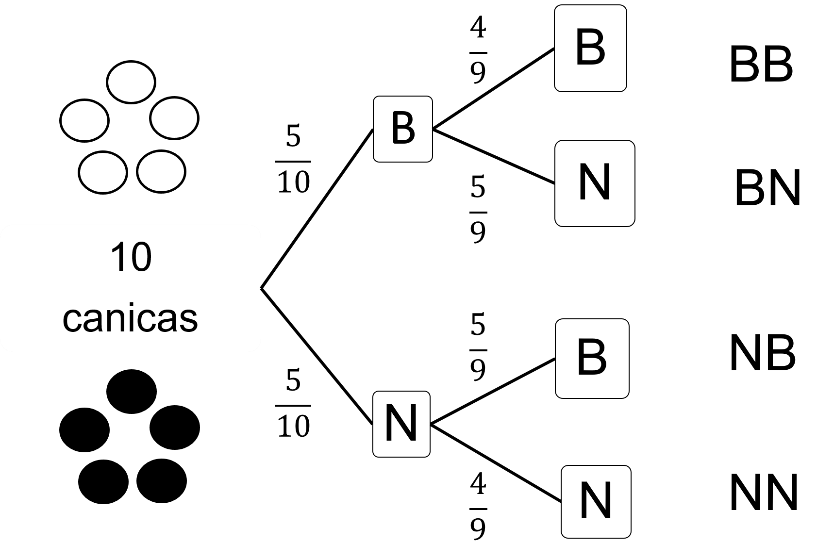
Después de extraer la primera canica y dejarla fuera de la caja, se extrae la segunda y las ramificaciones quedan de la siguiente manera.
Si la primera en salir fue blanca, 4 de las nueve restantes son blancas y 5 de los 9 restantes son negras.
Si la primera canica es negra, entonces 5 de las nueve restantes son blancas y 4 de los 9 restantes son negras.
Por ende, los resultados posibles después de las dos extracciones son:
Blanco, blanco.
Blanco, negro
Negro, blanco.
Negro, negro.
En otro ejemplo, se tiene que de una serie de 3 volados consecutivos hay 8 resultados posibles. Observa su representación:
Se comienza la ramificación con 1 de 2 resultados para “águila”, y 1 de 2 resultados para “sol”.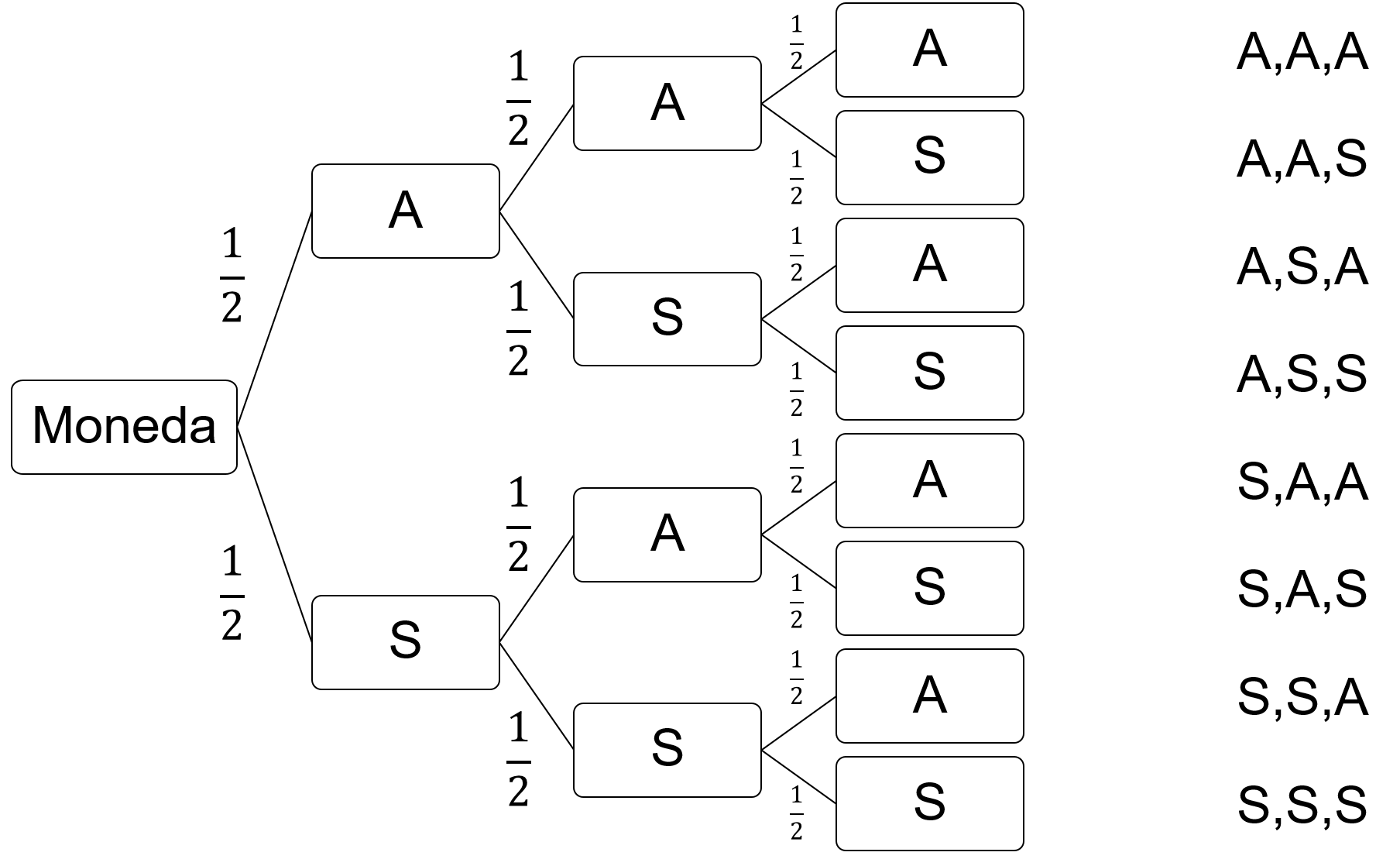
En el segundo lanzamiento se tiene de nueva cuenta 1 de 2 resultados para águila, y 1 de 2 para sol.
Y para el tercer lanzamiento se repiten los resultados anteriores.
De esta manera, el diagrama permite visualizar todos los resultados posibles después de terminado el experimento.
En este caso, se observa que son 8 posibilidades:
La primera posibilidad indica que puede salir 3 veces águila.
También se puede obtener águila, águila y sol
Águila, sol, águila.
Águila, sol, sol.
Sol, águila, águila.
Sol, águila, sol.
Sol, sol, águila.
Y Sol, sol, sol.
También existe otro tipo de situaciones en las que se pueden emplear las tablas de doble entrada.
Por ejemplo:
En el patio de la escuela se encuentran los alumnos del grupo “3ro A”.
Se quiere escoger un alumno al azar y ver a cuál taller pertenece.
Para hacer un análisis de probabilidad, la tabla de doble entrada queda de la siguiente forma: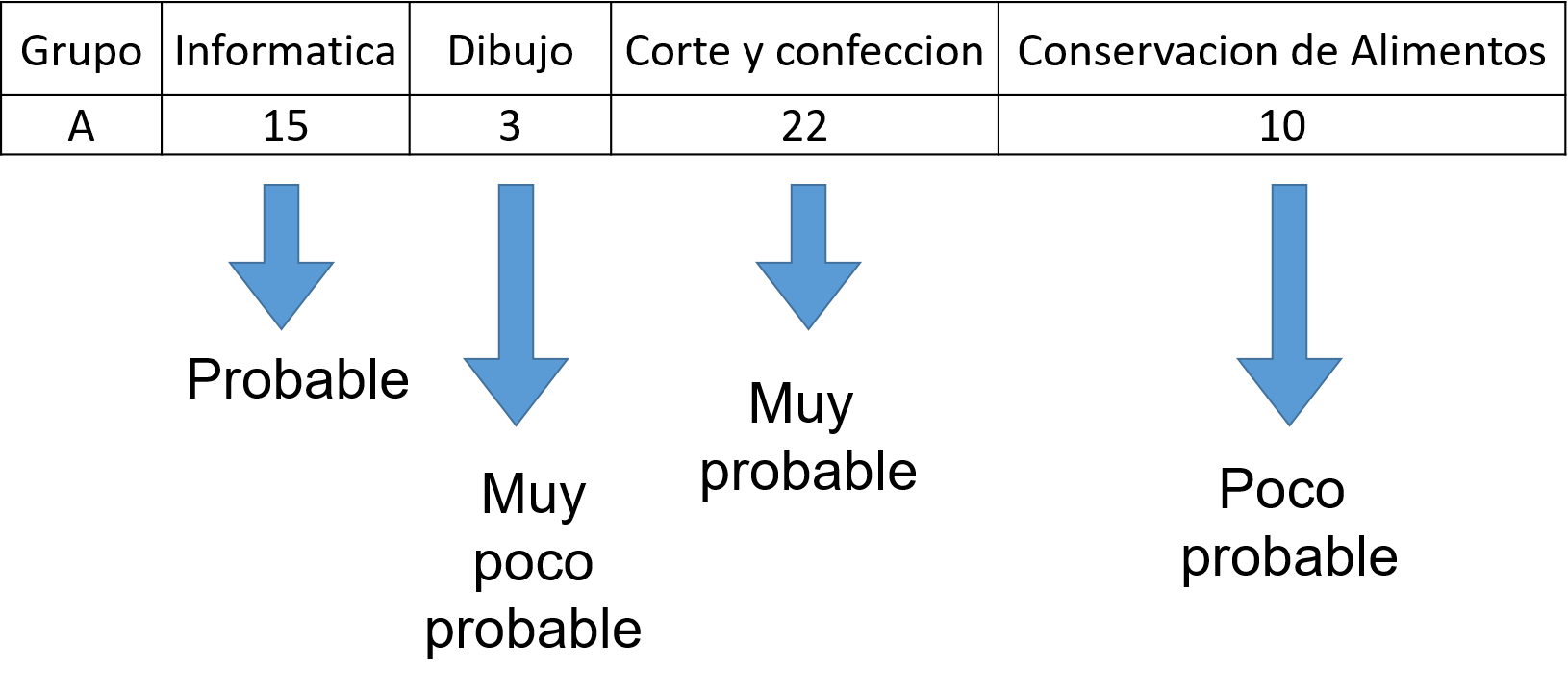
El Grupo A tiene 15 alumnos en informática, 3 en el taller de dibujo, 22 en el taller de corte y confección, y 10 en conservación de alimentos.
Ya con la tabla realizada, se puede conocer cuál taller tiene la mayor probabilidad y cuál tiene la menor al escoger a un alumno al azar.
Para denotar el grado de incertidumbre respecto al taller, se pueden usar oraciones como: “Es muy probable […]” o “La mayor probabilidad la tiene […]”.
Para informática, se puede indicar que es “probable” seleccionar un alumno al azar; para dibujo es “muy poco probable”; para un alumno del taller de corte y confección es “muy probable”, y “poco probable” encontrarse con un alumno de conservación de alimentos.
“La escala de la probabilidad”.
Considera que se tiene una escala de 0 a 1, como en la figura siguiente, en la cual se asigna un número a algunas expresiones relacionadas con el azar.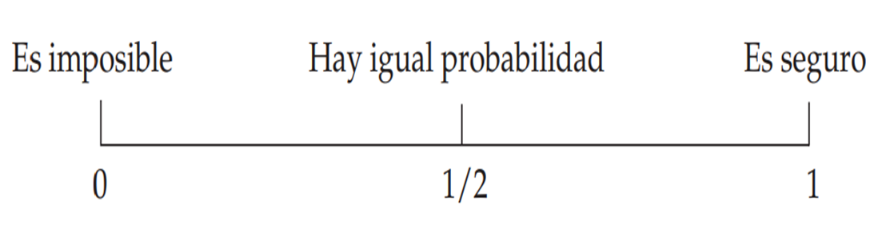
Pero ¿cómo se ubican en esta escala los términos que se ordenaron en el ejercicio anterior?
Una de las ideas fundamentales de la probabilidad en las nociones intuitivas acerca del azar, es que en el lenguaje cotidiano se expresan frases como: “Se espera que […]”, “Hay igual probabilidad…” o “Es bastante probable […]”, se normen dentro de una teoría matemática.
De tal manera, los eventos imposibles tengan probabilidad 0 y los eventos seguros probabilidad 1, de los que se asignan valores entre 0 y 1 ante las probabilidades de que sucedan.
Se tiene una bolsa opaca con 20 canicas, iguales en todos aspectos salvo en el color: 15 de ellas son blancas y 5 rojas. Si se agita la bolsa de tal manera que se mezclen bien las canicas y sin mirar adentro de la bolsa, se toma al azar una canica.
Entonces ¿cuál color de canica saldrá?
No se está seguro del color de la canica que saldrá, ya que el resultado depende del azar.
Y si se apuesta a favor de un color antes de sacar la canica, debe ser de manera racional y no confiando meramente en la suerte.
Así se debe determinar cuál de los dos colores tiene mayor probabilidad.
El anterior es un buen ejemplo del problema probabilístico.
Se tiene una experiencia aleatoria, en donde no se produce el mismo resultado cada vez que se repite en las mismas condiciones.
El problema consiste en determinar cuál de los eventos —“extraer una canica blanca” o bien “extraer una canica roja”— es más probable. En este caso la solución al problema es sencilla.
Son 15 canicas blancas contra 5 rojas; hay más posibilidades de escoger una canica blanca que de escoger una roja. Es decir, es mayor la probabilidad de escoger una canica blanca.
Dado que, en la bolsa, 15 de un total de 20 canicas son blancas, la probabilidad de sacar una canica blanca es de 3/4, 0.75 o 75%, según se exprese como una fracción, un decimal o en forma de porcentaje.
El problema anterior condujo finalmente a una consideración de la forma: Tal evento tiene “n” formas de ocurrir sobre un total de “N” posibilidades.
Este cociente, con algunas precisiones que se explican a continuación, se conoce como la “Fórmula clásica de la probabilidad”:
Si el que todos los eventos tienen condiciones iguales de ocurrencia.
Si se conoce el número total de resultados posibles “N”.
Y si se sabe el número de resultados favorables al evento que te interesa “n”.
Entonces, se puede ocupar la Fórmula Clásica de la probabilidad.
Se realiza esto para el ejemplo de escoger aleatoriamente a un alumno del Grupo “3ro A”, con relación a sus talleres, y se complementa la idea empírica ya formulada.
Primero se verifica si cumple con las condiciones: ¿Cualquier alumno tiene las mismas probabilidades de ser escogido?
Según el enunciado de la situación, todo el grupo está en el patio de la escuela y se puede seleccionar a cualquier alumno. Por lo tanto, todos los resultados son igualmente probables.
¿Cuál es el número total de resultados posibles?
Aunque no se tiene el dato de manera explícita, la suma de cada uno de los datos permite conocer el total de alumnos del grupo 3ro A.
Son 15 alumnos en informática, más 3 en el taller de dibujo, más 22 en el taller de corte y confección, y 10 más en conservación de alimentos para un total de 50 alumnos.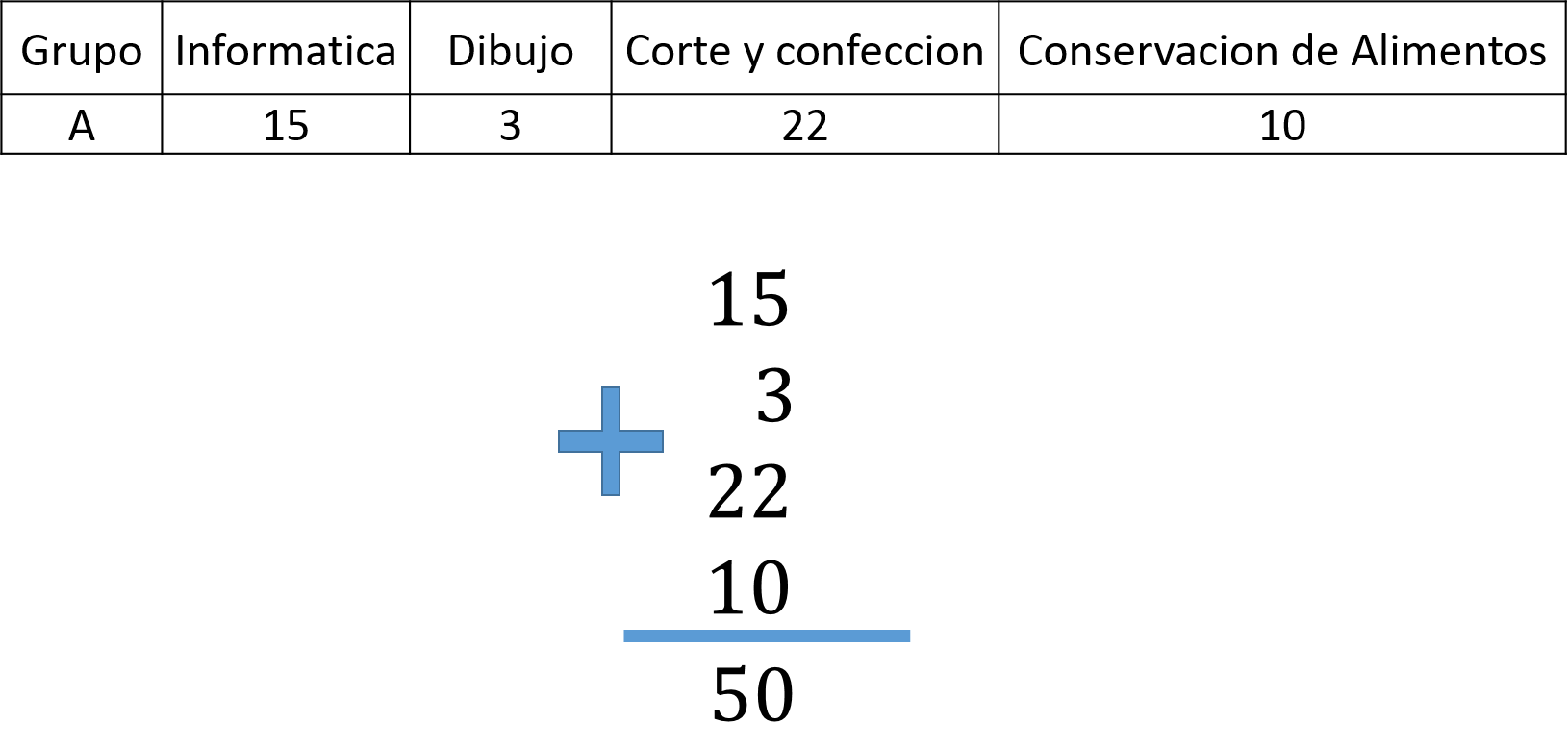
El número total de casos favorables al evento se encuentra en la tabla. Son 15 en informática, 3 de dibujo, 22 de corte y confección y 10 en conservación de alimentos.
Entonces, si todos los resultados son igualmente probables, la probabilidad se obtiene calculando el cociente:
Probabilidad de (A) es igual al número de casos favorables entre el número de total de casos.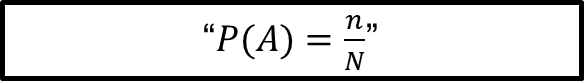
Para la probabilidad de escoger al azar un alumno del taller de informática se tiene que:
La Probabilidad de (i) es igual a casos probables que son 15, entre el número total de casos, que son 50.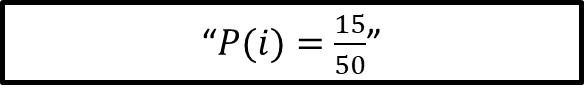
Se reduce la fracción a su mínima expresión para obtener la forma fraccionaria de la probabilidad, que es igual a 3 décimos.
Se hace la división de 3 entre 10 para obtener su forma decimal, o se multiplica por 100 para obtener su porcentaje, el 30%.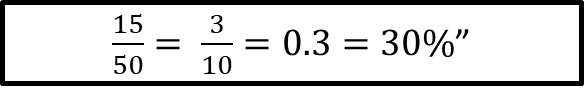
Para el resto de los talleres, el cálculo de la probabilidad clásica es: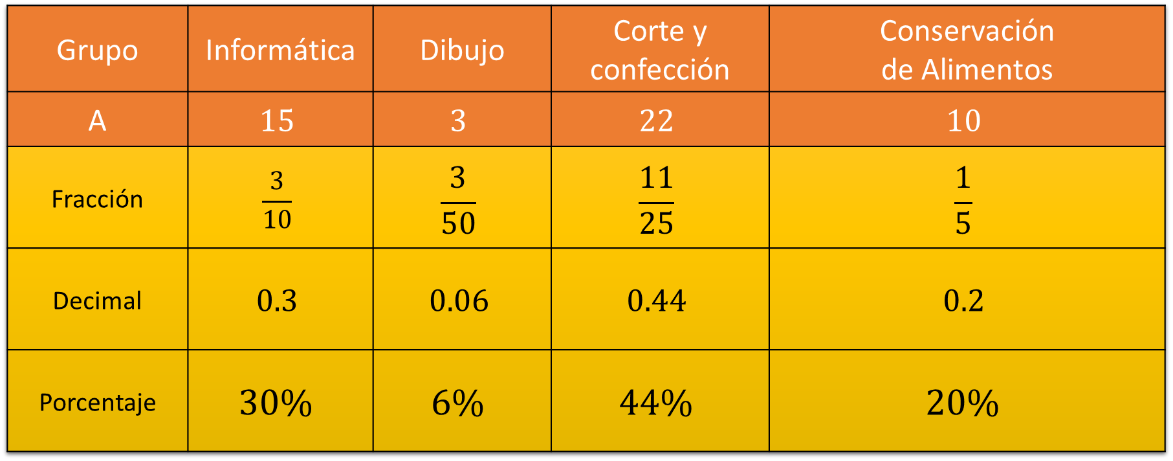
Dibujo son: 3 de 50, que es irreducible: 0.06 en su forma decimal que representa el 6% de las probabilidades.
Corte y confección, 22 de 50 y se reduce a 11 veinticincoavos: 0.44 en su forma decimal y representa el 44% de las probabilidades.
Conservación de alimentos con 10 alumnos de 50: Se reduce a 1/5 en forma de fracción, 0.2 en su forma decimal y representa el 20% de la probabilidad.
De este modo, ya se tiene la certeza matemática de los posibles resultados del experimento, y no solo una intuición del análisis de los datos.
Observa el siguiente video. - Probabilidad frecuencial de un evento
https://www.youtube.com/watch?v=Ld7RcoVl6Dk

La idea de simular consiste en explorar el comportamiento de una experiencia aleatoria observando otra experiencia equivalente, pero más fácil de realizar o de estudiar.
La situación que consiste en extraer al azar una o más canicas de una bolsa en donde hay diversos colores, es uno de los modelos universales de la probabilidad.
Esto se debe porque a través de él se puede representar y resolver casi cualquier problema donde intervenga un número finito de resultados posibles.
También puede utilizarse para simular casi cualquier experiencia aleatoria con las mismas características.
Por ejemplo, analiza “El problema del agente de ventas”:
Un agente comercial sabe que cada vez que visita un cliente tiene 20% de probabilidades de hacer dos ventas; 50% de probabilidades de hacer sólo una y 30% de no hacer ninguna.
Un día tiene cita con cinco clientes: ¿Cuánto puede esperar ganar ese día si por cada venta que realiza gana $20?
Para simular la situación del ejemplo, se ponen dos canicas azules, cinco blancas y tres rojas en una bolsa. Después, se extrae una a una al azar, cinco canicas de la bolsa, devolviendo cada vez dentro de la bolsa la canica que se consiguió antes de la siguiente extracción.
Dependiendo de lo que salga, se puede decir:
Si sale azul, el agente hizo dos ventas y ganó $40.
Si sale blanca, sólo hizo una venta y ganó $20.
Si sale roja, no hizo ninguna venta y no ganó.
Llevando una estadística de lo que ocurre al repetir varias veces el experimento anterior, se llega a estimar con alta exactitud la cantidad que el agente puede esperar ganarse ese día.
Se conoce otro ejemplo que, aunque es posible realizar el experimento en la vida real, se facilita con la simulación.
Cinco personas desconocidas se suben al elevador de un edificio de 10 pisos.
¿Es grande o es pequeña la probabilidad de que dos personas bajen en un mismo piso?
Para simular esta situación, se meten en una bolsa 10 pelotas marcadas con los números del 1 al 10, que representan los 10 pisos del edificio. Después, se extraen cinco pelotas al azar, devolviendo una a la bolsa cuando se consigue otra pelota, antes de realizar la siguiente extracción.
Los resultados que se obtengan muestran en cuáles pisos bajaron las personas y permite comprobar si hubo dos que descendieron en el mismo piso.

En algunos de los ejemplos de cálculo de probabilidades hay un elemento muy interesante: En un momento dado, un razonamiento del estilo: “la probabilidad de que esto junto con esto otro suceda”.
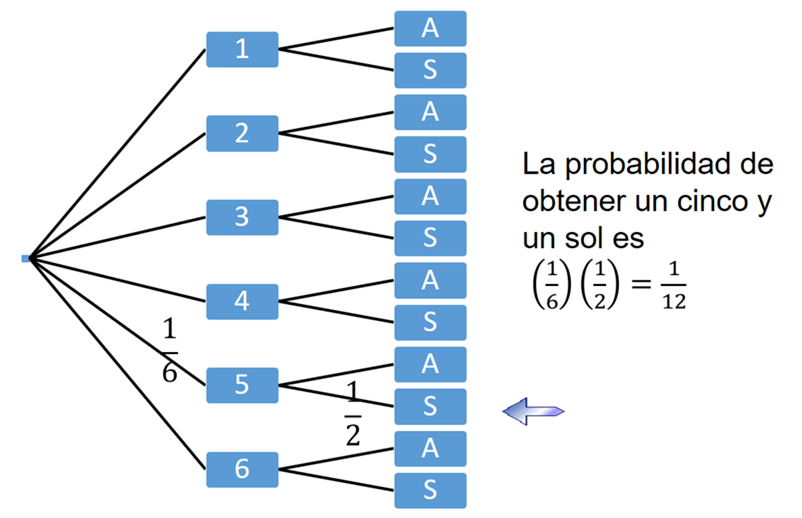
Por ejemplo, supón que se arrojan simultáneamente un dado y una moneda del que se quiere calcular la probabilidad de obtener un cinco y un sol.
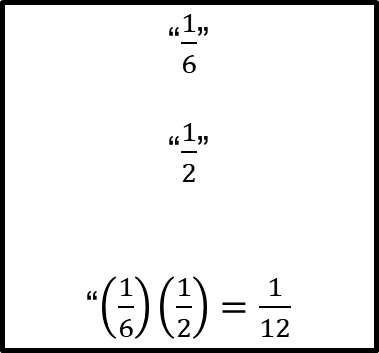
La probabilidad de obtener un cinco al arrojar un dado es 1/6, y la probabilidad de que salga sol en un volado es 1/2.
Entonces, la probabilidad de obtener un cinco y un sol al lanzar simultáneamente un dado y una moneda es igual a: 1/6 por 1/2 igual a 1/12.
En el diagrama de árbol del experimento se observa que al final son 12 resultados posibles, y solo 1 de ellos cumple con la condición de “cinco y Sol”.
¿Qué significa la condición de que los eventos A y B sean independientes? Que la ocurrencia de cualquiera de ellos no afecta la probabilidad de ocurrir del otro.
Dicha condición da por sentado que satisface el ejemplo anterior: Si sale cinco al arrojar un dado, esto no afecta la probabilidad de obtener sol al realizar un volado y recíprocamente, el resultado en el dado no afecta el del volado.
Pierre Simón de Laplace, un gran matemático francés y pionero de la probabilidad, afirmaba que esta disciplina es, en el fondo, “sentido común reducido a cálculos”.
Esta idea puede interpretarse como un proceso en donde las primeras apreciaciones probabilistas se transforman en conceptos y enunciados cada vez más precisos, a los cuales será luego posible aplicarles el poder analítico de las matemáticas.
El reto de hoy:
Para resolver dudas o ejercitar lo aprendido, te puedes apoyar en tu libro de texto.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.