Figuras en el piso
Figuras en el piso
Aprendizaje esperado: construye configuraciones utilizando figuras geométricas.
Énfasis: desarrolla la percepción geométrica al armar rompecabezas geométricos en una retícula cuadrada.
¿Qué vamos a aprender?
Aprenderás a construir configuraciones utilizando figuras geométricas.
¿Qué hacemos?
En la sesión anterior, se te pidió que tuvieras preparadas las figuras del recortable de la página 221 de tu libro de matemáticas. Esto lo ocuparás en esta sesión junto con tu libro de matemáticas.

Si olvidaste los recortables, solicita ayuda a un adulto para recortar las figuras.
Te cuento que el otro día Sebastián de primer grado, pensó lo que aprendió la sesión pasada al respecto de que las matemáticas están en todas partes. Le comentó a su familia que hay artistas, como el pintor Eduardo Terrazas o la gente de Teotitlán del Valle que usan la geometría en su trabajo. Su hermana le dijo que también en ciertos juegos de mesa se utilizan; como el billar, el ajedrez o incluso las canicas.

Este tipo de juegos ayuda a tener la mente bien ejercitada, el tablero de ajedrez está relacionado a la actividad de hoy.
Para esta sesión necesitaras: Tu libro de texto de matemáticas.
https://libros.conaliteg.gob.mx/20/P1MAA.htm
Ubica la página 175 que está en tu libro de matemáticas.

El tablero de ajedrez es también un piso; sólo que, sobre él, se mueven las piezas, ambos son una cuadrícula, es decir, están conformados por varios cuadros.
La diferencia es que la cuadrícula del piso de ajedrez es blanca y negra y la del piso de la zona de juegos es toda blanca.
Para que esa cuadrícula no se quede en blanco acomoda sobre ella las piezas del recortable. El libro pide presentar dos propuestas para acomodarlas, pero existen más de dos formas de hacerlo.
Primero, identifica las piezas del juego, tienes 2 cuadrículas, cada una tiene 12 cuadritos, también tienes las piezas del recortable que son 4 rectángulos y 6 que son como una “L” mayúscula, pero no es igual, recuerda que la L mayúscula tiene una “patita” más larga que la otra. En la figura del recortable las dos “patitas” son del mismo tamaño.
¿Cuántos lados tiene un rectángulo? 4 ¿Y la que parece “L”? tiene 6 ¿Recuerdas que en sesiones anteriores hiciste el ejercicio de formar una figura geométrica grande a partir de dos pequeñas?
¿Qué figuras puedes formar con la “L”? La L está formada por un rectángulo y un cuadrado, también podría estar formada por 3 cuadrados. En el libro dice que puedes usar cualquiera de los dos tipos de piezas pero que no puedes encimarlas ni dejar en blanco.
Podrías usar en una cuadrícula 4 rectángulos poniéndolos “paraditos”.

¿Podrías rellenar las cuadrículas sólo usando las “L”?

Si giras las piezas de cabeza o las volteas de lado, se pueden acomodar mejor y embonar bien, es como armar un rompecabezas. Ve jugando con los distintos acomodos de las figuras sobre la cuadrícula ¿Será posible usar las dos figuras en una sola cuadrícula?
Observa los siguientes ejemplos.
Ejemplo A
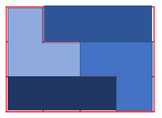
Ejemplo B
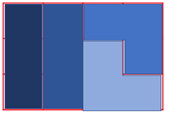
Aún hay muchas formas de acomodar las piezas, es momento de llenar la tabla que se encuentra debajo. En el diseño A hay 2 rectángulos y 2 “L”.

La diferencia es que en el diseño de los rectángulos están “paraditos” y en el otro acostados. En cualquier diseño que utilices para rellenar la cuadrícula, ¿Consideras que siempre tienes que utilizar 3 rectángulos y 1 “L”?
Para descubrirlo, intenta rellenar la cuadrícula con 3 rectángulos y 1 o 2 “L”. ¿Qué otro acomodo, además del que ya hiciste al inicio, propones para 4 rectángulos?
Si al inicio se pusieron 4 rectángulos en forma vertical, ahora la propuesta es con 3 rectángulos “acostados” y 1 vertical.

¿Se podrían hacer otros diseños con otras figuras geométricas?
Vas a quitar las figuras que usaste en esta sesión y vas a imaginar en esta cuadrícula que otras figuras podría haber.
Pueden ser triángulos, como en los diseños de tapetes. 2 triángulos unidos te dan un cuadrado.
Entonces también podrías rellenarlo con puros cuadrados.
El reto de hoy:
Arma tus propios rompecabezas, sigue jugando en casa a diseñar hermosos pisos.
También puedes fijarte si el piso de tu casa tiene figuras geométricas y si es distinto al del baño, por ejemplo.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas
